基于距离多普勒二维稀疏重构的生命体征目标成像算法研究

肖 磊,徐 磊

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

雷达作为利用电磁波去进行探测和识别待测或可疑目标的一种工具,从18世纪出现以来,得益于其能够持续不间断、稳定地进行探测的优点,逐渐受到人们的重视,而其中生命体征雷达则是研究热点之一。现有的人体识别和定位技术都是基于摄像机镜头和计算机的视觉信号处理方法,这些方法均具有易实现的优势,特别是在计算机视觉分析领域已经有了许多年的研究成果积累。虽然此类设备准确性较高,但其缺乏隐私,对环境依赖性较强,在雨天、雾天或光线较差等环境条件下存在观察的不确定性。与此相比,生命体征雷达凭借其尊重个人隐私、受环境影响小和成本低的优点将会有更广阔的应用前景。针对生命体征雷达的成像定位技术,其相关研究主要有3类：基于超宽带(UWB)的研究[1]、基于调频连续波雷达的成像定位[2]和基于SAR成像的目标定位研究[3]。

对于生命体征雷达探测目标的定位技术,国内外学者研究较多集中在通过成像或利用波束形成技术和雷达测距来进行目标的位置确定,但这些研究局限于区分人与环境静止杂波干扰,而无法区分人体和非人体动目标,易将具有多普勒的运动目标误判为人体目标。针对该场景,本文采用基于距离多普勒二维信息的稀疏重构成像算法,实现了对非人体的动目标干扰消除,同时完成人体目标的二维空间成像定位。

1 压缩感知原理

随着现代科学技术的不断发展,各种信号处理系统要面对的处理数据量将不断增加;而传统的数据采样定理奈奎斯特采样定理在处理所获取的数据时,会要求该信号的采样率一定要是此信号的信号带宽的两倍及以上[4],所以此方法会对信号处理的软件及硬件提出较高的要求,实现难度也是比较大的。

因此,为了更快速、便捷地来处理所获得的数据,压缩感知这一理论便应运而生,Donoho与Candes等人提出该理论方法,充分利用了原始信号的稀疏性。所谓的稀疏性是原始信号在某个域上只有较少的有限个元素不为0,其余都是0。那么这样的信号就具有很好的稀疏性或者可压缩性[4]。这一理论指出,如果存在某个变换域矩阵Φ,能够使1个N维信号x在Φ域中表示为1个K稀疏信号,即x=Φα,α仅有K(K≪N)个非零元素,其他元素等于零或接近于零。则利用与Φ非相干的测量矩阵Ψ对x进行M(M≪N)次压缩采样结果y=Ψx=ΨΦα,便可通过求解1个稀疏约束的欠定性方程组以较高的概率重构出原信号[5]。

对于雷达的信号处理分析而言,雷达的回波信号作为探测目标或场景的数据集,在某一变换域上往往具有稀疏的特性。本文所用实验雷达检测人体目标的实验场景中,待测的人体目标在探测环境中是稀疏的,即在最终成像图中为稀疏的。研究了具体的回波信号后,可以发现,经过快速傅里叶变换(FFT)处理,目标信号在频域上表现为1个能量点,从整个频域范围来看,目标信号便表现出了稀疏性,进而会发现在距离多普勒二维的分辨场景中,目标仅仅占了少数的几个分辨单元,远远少于整个距离多普勒二维的分辨单元总数,因此,待测人体目标在距离多普勒二维信息中是稀疏的。

设信号矢量x=[x(1),x(2),…,x(N)]T∈CN×1,可表示为1组基Φ=[φ1,φ2,…,φL](一般为标准正交基)的线性组合,即：

(1)

式中：α是由变换域系数αi构成的L×1维向量,α=[α1,α2,…,αL]T;φi∈CN×1,i=1,2,…,L。

根据式(1)的表示形式,可以发现x与α其实表示的是相同的一个信号,但是是在不同的2个域上的表示方式,其中x为信号的时域表示,α为信号x在Φ域的投影表示。

假设x在矩阵Φ上的等价表示α中只有少数K个非零的值,且α的支撑集supp(α)={i：αi≠0}满足：

‖α‖0=|supp(α)|=K≪N

(2)

则称x为K稀疏信号,Φ为对应的稀疏基矩阵。式(2)中,‖α‖0表示α中非零元素的个数,‖·‖0为向量的l0范数,|·|表示集合的势。如果信号x自身满足稀疏条件时,则对应稀疏基矩阵为Φ=IN×N的N阶单位矩阵。

上述理论原理是对信号比较直接和准确的稀疏性表示的一个度量准则。除此之外,压缩采样是压缩感知应用于雷达信号处理中需要关注的一个重要方面,其对信号降采样和信号重构等关键步骤均有较大影响,主要体现在如下几方面：(1)获取回波信号线性测量值;(2)对回波信号进行降维处理,完成对其的压缩操作;(3)在降维压缩处理过程中,保留完整的原始回波信息,并将其用测量值表示;(4)与稀疏基矩阵构成感知矩阵,为压缩感知重构算法重建原信号提供依据。

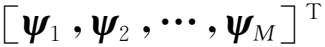
(3)

矩阵形式为：

y=Ψx

(4)

假设x为1个一维信号,长度为N,稀疏度为k(即含有k个非零值),设定测量矩阵为Ψ(M×N的二维矩阵),一般的自然信号x本身可能不是稀疏的,需要在特定稀疏基上进行稀疏表示：

x=Φα

(5)

式中：Φ为稀疏基矩阵;α为相应的稀疏系数(k≪N)。

所以最终可得到压缩感知的计算方式：

y=Ψx=ΨΦα=Θα

(6)

式中：Θ=ΨΦ∈CM×N,称为感知矩阵。

图1为压缩采样示意图。

图1 压缩采样示意图

另外,根据压缩感知理论,测量矩阵Ψ与稀疏基矩阵Φ是不相关的,即基于测量矩阵的采样过程不会根据回波信号的不同而改变。因此,若在采样过程中出现改变,有其他信息添加进来,最终的结果不会随之改变,故压缩采样本质上亦为非自适应的线性测量。

2 基于距离多普勒二维信息的稀疏重构算法

图2为本文所提出的基于距离多普勒二维信息稀疏重构成像算法的流程图。首先,在得到矫正的雷达回波信号之后,设置雷达系统探测角度为-60°～60°,以1°为间隔分为121个角度分量,对各个搜索角度θ,分别去计算相应的导向矢量a(θ)：

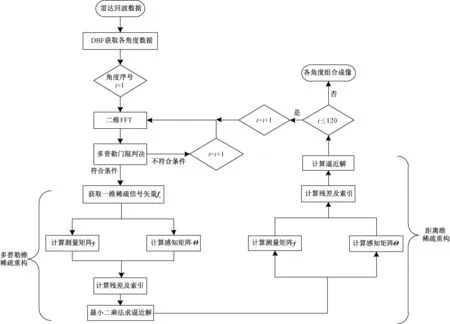
图2 基于距离多普勒二维信息稀疏重构成像算法流程图

a(θ)=[1 ej2πdsin(θ)/λ… ej2π(m-1)dsin(θ)/λ]

(7)

式中：d表示天线阵元的间距;λ表示雷达工作波长;m为雷达天线阵元个数;角度θ取探测角度范围内的121个角度分量。

则加权之后各角度的回波信号s(k)为：

s(k)=a(θ)HB(k)

(8)

式中：B(k)为校正过后的雷达回波信号。

然后,针对每个角度的信号矩阵计算1 024点的二维FFT,探测范围内目标的距离和多普勒信息都能获取。设置雷达系统对应的距离门为0.293 m,速度分辨率v可按下式计算：

(9)

式中：fm为慢时采样率;N为FFT点数;f0为雷达载频。

最终求得v=0.005 m/s。由结果可知,本雷达系统能探测到微弱多普勒信号,说明了检测人体呼吸等生命体征信号的可实现性。

通过计算FFT,可以发现成像时,目标在二维能量图上是稀疏的。利用此特点,可以对目标信息进行稀疏重构,以此去除杂波干扰。

具体算法处理的过程介绍如下：

步骤1,对各角度的回波信号s(k)计算距离多普勒二维N点的FFT,得到矩阵RTM[N,N]。

步骤2,对所求的二维FFT能量矩阵,寻找能量最大点,横坐标对应目标的多普勒,纵坐标对应目标的距离;针对非人体的运动目标,所产生的多普勒fd比人的微弱生命体征信号的多普勒fp要大得多,即fd>>fp;所以,本系统算法处理开始设定一个速度门限vth=0.015 m/s;若探测范围内目标速度大于此门限,则视为干扰动目标,该角度雷达回波信号置为零。

步骤3,对RTM[N,N]每一行求IFFT,得到N个一维原始稀疏信号矢量fi(i=1,…,N)。

步骤5,计算感知矩阵Θ=ΨΦ∈CM×N,Φ=(FFT(e(N,N)))-1为频域稀疏基矩阵,(·)-1为求逆操作,FFT(·)为计算矩阵的FFT,e(N,N)为生成N×N的单位矩阵。

步骤6,此生命体征探测场景,令稀疏度k=1,初始化残差r0=y。

步骤7,计算残差r和感知矩阵中的列φj的内积,找出其中最大值的索引λi：

λi=argmaxj=1,2…,N|〈ri-1,φj〉|

(10)

步骤8,计算本次重构集合为Θi=[Θi-1,φλi],利用最小二乘法[6]可算出原始稀疏信号fi的逼近解：

(11)

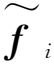
3 实验结果分析

为验证本文算法,设计2种场景下的实验：场景一：单人体目标单干扰运动目标场景;场景二：双人体目标场景。

场景一布置如图3所示,电风扇作为非人体的动目标放置于距雷达1.7 m处,角度距雷达中心为13°左右;待测人体目标位于距雷达2 m处,角度距雷达中心约14°。待测目标正常呼吸,电风扇正常运行。

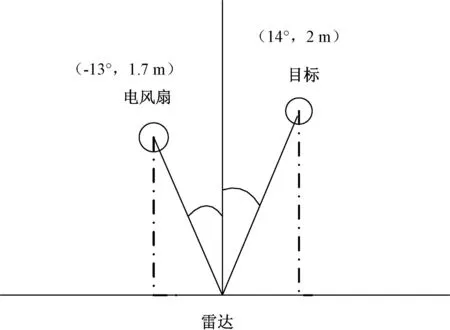
图3 实验场景图一

运用传统动目标显示(MTI)方法成像图如图4所示,会有多径效应,产生一定的虚影,影响目标判断;同时,会发现电风扇和人体目标同时被检测到,而雷达的生命体征探测只针对人体目标,电风扇的成像点容易误判为人体目标。

图4 传统方法成像

而如果采用常用的稀疏重构正交匹配追踪(OMP)算法,最后成像结果如图5所示,左侧成像点为电风扇,右侧成像点为人体目标。与图4传统方法成像图相比,基于距离维稀疏重构OMP成像算法抑制了多径效应,去除了干扰杂波,实现了雷达探测范围内动目标的成像与定位,但是该方法会将具有多普勒特征的目标都进行成像,并误判为人体目标。

图5 基于距离维稀疏重构成像图

利用本文提出的基于距离多普勒二维信息稀疏重构算法进行成像定位,如图6所示。因为加入了多普勒维的判决,与图5基于距离维稀疏重构成像图相比,抑制了非人体的其他动目标的干扰,可获得较好的成像效果。从图中可以得到人体目标在角度为14°、距离为2.051 m时,测角误差为0°,测距误差为0.051 m,实现了人体目标的二维空间成像与定位。

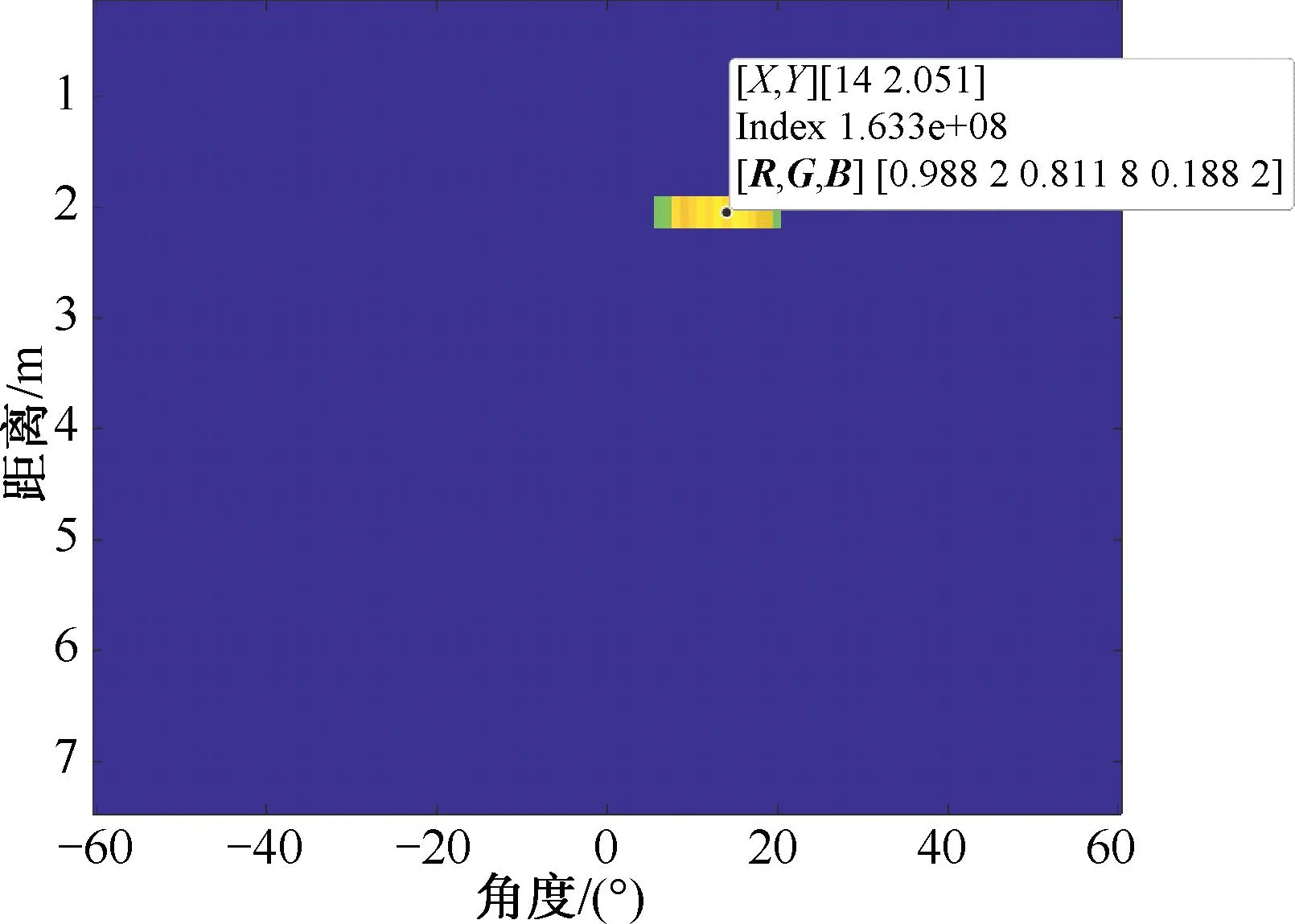
图6 基于距离多普勒二维稀疏重构成像图

针对双人目标场景二,设置如图7所示。

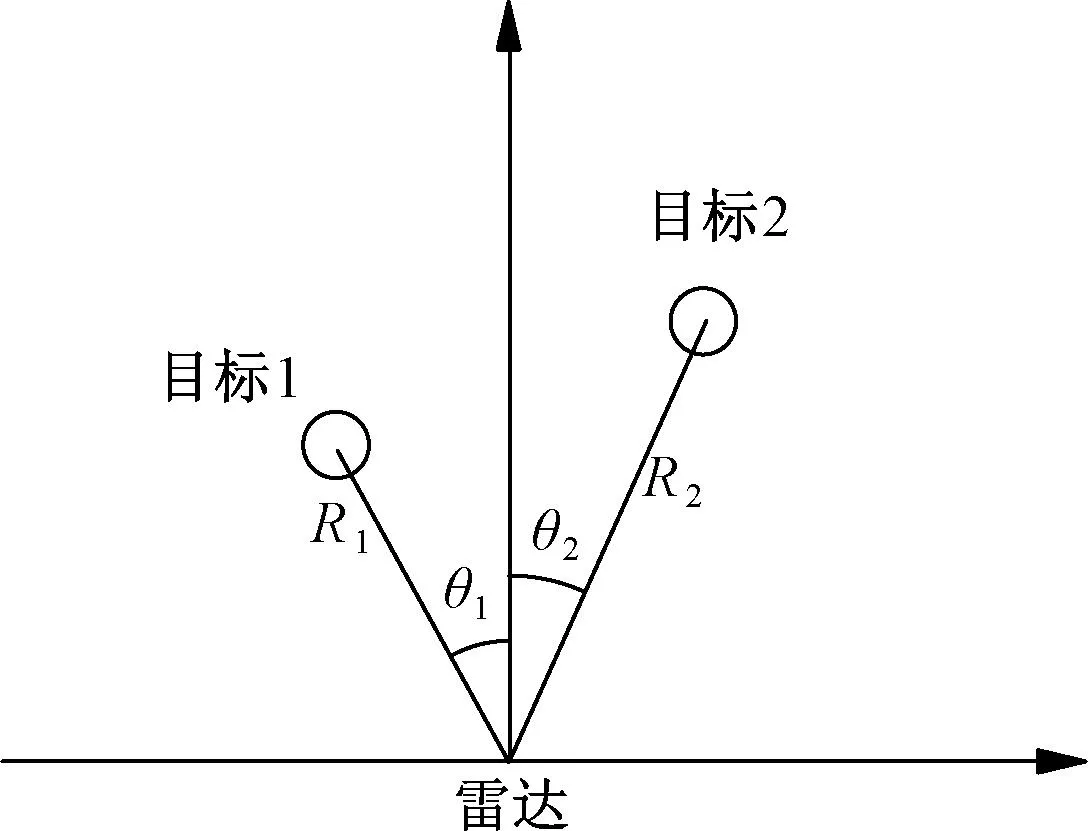
图7 双人实验示意图二

待测目标1与雷达间的距离约为R1=1.5 m,与雷达法线方向的夹角值约为θ1=-17°。类似地,设置待测目标2与雷达间的距离约为R2=2.5 m,与雷达法线方向的夹角值约为θ2=9°。

运用本文所提出的基于距离多普勒二维信息稀疏重构算法进行成像的结果如图8所示。从图中可以得到2个待测目标的距离以及所在角度的信息。从目标的成像定位图中可以得到,待测目标1的实际测距结果为R1=1.465 m,实际测角结果为θ1=-18°,测距误差为0.035 m,测角误差为1°;待测目标2的实际测距结果为R2=2.344 m,实际测角结果为θ2=10°,测距误差为0.156 m,测角误差为1°。

图8 基于距离多普勒二维稀疏重构成像定位图

通过实验结果分析可以得出,针对传统成像方法和OMP算法不能有效抑制杂波和运动干扰目标影响的缺点;本文算法成像效果较好,场景一有效抑制了运动物体的干扰,在存在较小误差的前提下能定位人体目标;场景二中双人目标的探测也获得了较好的成像定位效果。

4 结束语

与传统接触式生命体征测量不同,非接触式生命特征雷达的探测是持续不间断的,能提供长时间的探测数据,并且不容易受外界环境因素的影响,也尊重了检测目标的相关隐私。正因为这些优点,使得非接触式生命体征[7]的测量技术在现今人们越来越重视身体健康的社会得到广泛研究。本文研究了一种基于距离多普勒二维信息稀疏重构的成像算法,指出了压缩感知原理在保证对获取数据以不高速率处理时,能较完整地突出信号数据的内容和特点,可有效降低数据处理及分析过程中冗余的代价。利用稀疏重构相关理论研究成像定位算法,并对比了传统MTI、OMP算法的成像效果,有效抑制了人体目标外的杂波以及运动物体目标的干扰,验证了本文算法的有效性。