短波多音信号并行干扰消除解调算法

李 星,张利强,盛 兴,张广军

(解放军63891部队,河南 洛阳 410073)

0 引 言

由于短波通信传输距离较远,通常可达几千km,且抗干扰能力较强,因此广泛应用于各种军事远距离通信系统中[1],对短波通信信号的截获与解调并获取有用的信息是现代信息战的主要军事行为。

短波信道是一种多径衰落信道,经过电离层反射传播后接收到的信号是不同时频偏移以及衰落等多个分量的组合。短波通信的多径时延往往达到ms级别,多径时延导致接收信号发生符号间串扰,且无法通过增加信噪比的方式进行削弱。因此许多短波通信系统均使用多音并行传输策略,通过延长短波系统的符号持续时间,达到抑制多径影响的效果。同时通过多音并行传输策略扩展信号带宽,提升信息传输速率,满足不同业务对于传输速率的需求。常用的短波多音并行传输系统有MIL-STD-188 110A(16音、39音)、Link11A、ADVNT等[2-5],短波多音通信系统可以通过快速傅里叶变换(FFT)的方式进行调制和解调,但部分短波通信系统特殊的帧结构使其无法满足FFT映射时的载波正交条件。传统算法通过将帧持续时间截断的方式实现各子载波正交[4-5],这种方法降低了信号的时间分集增益。针对这一问题,我们研究了多音信号子载波非正交的产生机理,提出了一种并行干扰消除解调算法,实现了载波非正交条件下的多音信号解调,仿真实验验证了所提算法的有效性。

1 短波并行多音传输系统

1.1 问题的提出

并行多音传输系统的调制解调过程为：发送端的数据通过串并变换,将串行数据流转化为多路低速的并行数据流,将并行数据经过星座图映射后分别使用多个载波进行调制,信号调制通常使用快速傅里叶逆变换(IFFT)的方式来完成。

将调制数据bit经过星座映射后得到的数据符号调制到若干个子载波上,可以写成如下的复数形式：

(1)

式中：ωn=ω0+nΔω,为第n个子载波的频率;dn(t)为第n个子载波上的复数信号;Nc为载波个数,其在一个符号周期内为定值。

设信号采样频率为1/T,则有：

(2)

将公式(2)与离散傅里叶反变换(IDFT)进行比较：

(3)

可以看出,若把d(n)看作频域采样信号,s(kT)为对应的时域信号,此时基带信号与快速傅里叶逆变换(IFFT)运算表达式非常相似,此时多音信号的载波间隔为：

(4)

从公式(2)～(4)可以得出,若多音信号载波频率间隔为Δω,且符号周期为T,则多音信号各子载波满足正交特性,而且可以使用DFT的方式来进行调制解调。

多音信号对频偏较为敏感,由于短波信道条件恶劣,使用多音并行方式进行传输时,会将部分音设置为单音信号,用于对接收信号进行频率校准,同时部分音设置为帧同步音,接收端进行符号位置同步。

以Link11A信号为例,其使用16个音,其中605 Hz为单音导频载波,不调制信息。2 915 Hz载波为帧同步音,每个突发开始后2 915 Hz音相位调制信息为0和π翻转5次,用于帧同步。935～2 365 Hz每隔110 Hz共14个载波,加上帧同步音共15个载波用于数据段调制信息。Link11A的帧周期为13.33 ms和22 ms 2种,各个载波之间的间隔均为110 Hz[5]。通过前文分析可知,当多音间隔分别为75.018 8 Hz或45.454 5 Hz时满足子载波正交条件,可以使用离散傅里叶变换(DFT)的方式进行调制解调,但Link11A信号2种帧周期均不满足正交条件,存在多音串扰现象。

使用Link11A系统标准调制相位信息,设置帧周期为13.33 ms,采样率为14.08 kHz,每帧采样点数为187,接收端提取1帧数据,经过补0后通过256点FFT运算的方式进行相位映射,结果如图1所示。

图1 Link11A信号多音串扰

从图1可以看出,由于Link11A信号不满足载波正交条件,直接使用DFT算法进行解调后不能恢复调制信息。为了使用DFT算法进行解调,传统算法通过截断帧周期的方式恢复载波间的正交条件[4-9]。将13.33 ms的帧信号数据截断为9.1 ms,使用128点的FFT进行相位映射。将22 ms的帧信号数据截断为18.181 8 ms,使用256点FFT运算进行相位映射。可以看到,该方法会降低信号的空间分集增益。

针对这一问题,我们提出一种基于并行干扰消除策略的非正交多载波信号解调方法,利用了信号的整帧数据空间分集增益,进一步提高了信号解调性能。

1.2 FFT运算载波恢复

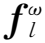
(5)

式中：l为帧长度;ω为载波的数字频率,若其真实频率为fc,则ω=2πfc/Fs,Fs为信号的采样率,则公式(2)可以改写为：

(6)

式中：NC为多音信号的载波个数;d(k)为第k个载波;ω(k)为第k个载波的数字频率。

接收端对多音信号S进行FFT运算,提取第k个载波的调制信息,忽略噪声相,其公式为：

(7)

在实际运算时,只提取包含调制载波的运算结果,将公式(6)、(7)合并,结果为：

(8)

该载波的调制相位信息为：

r_a(k)=p(r(k))

(9)

式中：p()为提取复信号的相位。

1.3 多音信号载波干扰并行消除

由公式(6)、(8)整理多音信号的发射和接收的数学关系,忽略噪声相,得到：

(10)

式中：r(1×NC)=[r(1)…r(NC)],表示接收信号各载波调制信息经过正交解调后的结果。

令：

(11)

d=[d(1)d(2)…d(NC)]

(12)

则公式(10)可以写为：

r(1×NC)=dFFH/l

(13)

Link11A信号由于不满足子载波正交条件,因此FFH/l不是单位矩阵,存在子载波干扰,无法直接用FFT运算提取调制信号的相位信息。

研究公式(13)可以得出,构建迫零均衡矩阵,将FFH/l映射为单位矩阵,就可以消除载波之间的干扰,而不需要对原始信号进行截断。

定义矩阵：

于是学生不断把原有的角进行两等分、三等分，直到细分到1度，至此已把一个直角平均分成90份，其中一份就是1°。

M=FFH/l

(14)

则公式(13)可以写为：

r(1×NC)=dM

(15)

得到：

(16)

由于矩阵M满足Toepltiz条件,因此该矩阵是可逆的。合并公式(7)和公式(16)得到接收信号的处理流程为：

(17)

值得注意的是,公式(17)中FM-1只与采样率和多音信号传输协议相关,与调制信息无关。对特定传输系统帧数据进行解调时,可将矩阵分量FM-1提前计算并保存在本地,在进行解调运算时直接将帧数据和本地数据按照公式(17)进行运算即可实现解调。

2 多音信号并行干扰消除解调算法

2.1 算法原理

前文论述了多音并行信号的载波干扰产生机理,在此基础上,提出了基于迫零均衡的并行载波干扰消除解调方法(PICA)以及一种基于多音信号并行干扰消除解调算法,算法以Link11A为例进行流程描述。

2.2 算法流程

输入：接收基带信号r,采样率Fs,帧周期Tf。

(1) 根据文献[10]算法进行突发检测;

(2) 根据文献[11]、[12]算法进行多普勒音频率估计;

(3) 依据估计的多普勒频率对信号进行频率校准;

(4) 按照文献[5]方法,依据同步音信号对接收信号进行帧同步,得到一帧数据r;

(5) 按照公式(8)对帧数据r进行载波恢复;

(6) 按照公式(14)构建干扰消除矩阵;

3 算法仿真

为了验证算法的有效性,生成13.33 ms帧周期的Link11A信号,设置采样速率为14.08 kHz,信噪比10 dB。使用3种方法进行解调,FFT补零算法将每帧187个采样点信号补零后进行256点FFT运算,PICA使用每帧187个采样点直接进行计算,FFT截断算法将每帧187个采样点信号截断为128个点后进行FFT运算。使用3种算法对信号进行解调,并将解调结果归一化,结果分别如图2(a)、(b)、(c)所示。

图2 3种算法解调结果

从图2(a)可以看出,由于载波干扰的存在,难以正确地恢复原始相位调制信息。从图2(c)可以看出,截断FFT算法以及PICA算法能够正确恢复原始相位调制信息。

为了比较PICA算法和截断数据FFT算法的误符号率性能,分别使用2种算法对13.33 ms和22 ms帧周期Link11A信号进行解调,统计不同噪声情况下的解调误码率,2种帧长度误符号率性能结果分别如图3(a)、(b)所示。

图3 2种帧长度误符号率性能

从图3可以看出,所提算法使用了整周期信号数据,时间分集增益大于截断FFT算法,误符号率性能较好。

为了比较本文算法与补零FFT算法,截断FFT算法的运行复杂度,按照表1的参数配置信号和算法,帧数为10 000,运行本文算法时直接调用根据帧格式提前计算好的矩阵FM-1对生成信号进行解调。分别统计3种算法的运行时间,结果如图4所示。

图4 3种方法运行时间

从图4可以看出,所提算法与截断FFT算法运行复杂度相近。

4 结束语

针对传统算法采用截断每帧信号的方式恢复载波正交条件后,使用FFT算法解调并行多音通信系统,削弱了信号的空间分集增益的问题。提出一种基于并行干扰消除策略的多音信号并行解调算法,通过构建干扰消除矩阵,在不牺牲信号帧长度的前提下实现多音并行信号的解调,通过对生成的Link11信号进行仿真验证了所提算法的有效性。

所提算法对采样率没有严格限制,构建的干扰消除矩阵只与信号帧格式有关,与调制内容无关,可以根据需要解调的多音信号帧格式构建干扰消除矩阵保存在本地,使用时直接调用即可,方便工程实现。