动态深度神经网络的硬件加速设计及FPGA实现*
2024-03-26任轶群范毓洋张嘉诚
王 鹏,任轶群,范毓洋,张嘉诚
(中国民航大学a.民航航空器适航审定技术重点实验室;b.电子信息与自动化学院;c.安全科学与工程学院,天津 300300)
0 引 言
卷积神经网络(Convolutional Neural Network,CNN)为基础的计算机视觉算法,在汽车自动驾驶、无人机图像识别、人体行为识别等领域有着广泛的应用[1-3],典型的卷积神经网络有AlexNet、VGGNet、GoogLeNet和ResNet等[4]。为了使CNN网络获得更好的精度,模型引入了更深层次的网络架构,导致正向推理过程所需要的计算复杂度增加,边缘设备难以高帧率地运行CNN网络[5]。实际应用中图像的特征识别难度不同,一些特征明显的图像只需要较少层数的网络即可准确识别[6]。为此,动态深度神经网络[7-9]通过在CNN中插入侧分枝(BranchyNet)分类器,允许交叉熵损失满足一定置信度的简单图像提前退出,减少不必要的特征提取次数,提升CNN模型在边缘部署的计算效率。BranchyNet的加入虽然减少了识别部分图像的计算量,但在边缘平台部署动态深度神经网络仍面临计算量大、算法复杂度高等问题。
现场可编程门阵列(Field Programmable Gate Array,FPGA)有着强大的并行性,不但可以数据并行还可以数据流并行,能够满足卷积神经网络的大量并行计算需求,并且具有低延时和低功耗的特性,还可以通过硬件适应算法的特性[10],设计针对特殊算法的加速电路。因此,FPGA可以很好地契合动态深度神经网络在边缘部署的需求。在FPGA加速神经网络方面,Venieris等人[11]采用同步数据流架构(Synchronous Dataflow Model)设计了一种将CNN模型计算任务映射到FPGA平台的流水处理方法,为了避免因数据缺失而导致流水线停顿,将需要加速的CNN模型权重和各层之间的特征图全部缓存到片上,但因为片上内存受限,此类方法只能适用于规模较小的CNN模型。Li等人[12]提出一种多FPGA组成FPG-A集群的架构,虽然可以达到较高的吞吐率以及很高的计算能力,但由于需要多个FPGA平台协作完成,不适用于边缘计算的应用场景。Liu等人[13]使用Winograd算法提出了一个在FPGA上运行的Winograd算法与脉动阵列结合的架构,需要专门的访存子系统,设计较为复杂,并且Winograd算法只能适用于步长为1的卷积,因此通用性受限。
本文基于FPGA设计了一种面向嵌入式平台的针对插入侧分支后具有动态深度的ResNet110网络(BranchyNet-ResNet110,B-ResNet110),并从定点量化、并行运算、流水线化等3个方面对模型进行加速,针对提前退出机制设计专用的加速电路。在XILINX xc7z030ffg676-2芯片上对上述内容进行实现,首先设计针对卷积层和池化层的通用IP,以及提前退出模块的专用加速IP;然后将IP组成片上系统(System On Chip,SOC),完成B-ResNet110部署;最后分别从计算速度、资源利用率、识别准确率等方面对设计进行综合性能分析。
1 动态深度神经网络
本设计中的动态网络是带有提前退出分支BranchyNet的神经网络。图1给出了B-ResNet110的结构,可以看出该动态网络由主干网络和两个分支网络组成。其中,主干网络是ResNet110网络,可分为5个部分。第一部分是一个16通道卷积核尺寸3×3步长(stride)为1的卷积层。第二部分至第四部分,由18个常规残差模块(plain residual block)组成,通道数分别为16通道,32通道,64通道。不同的是,第三部分和第四部分的第一个残差模块需要对输入特征图进行下采样操作。第五部分为池化层和全连接层组成的输出层。第一个分支网络(BranchyNet 1)插入在第二部分之后,第二个分支网络(BranchyNet 2)插入在第三部分之后。分支网络1由一个残差模块、一个全连接层、一个交叉熵损失函数层组成。分支网络2由一个3×3卷积层、一个全连接层、一个交叉熵损失函数层组成。交叉熵损失函数如公式(1)所示:
(1)
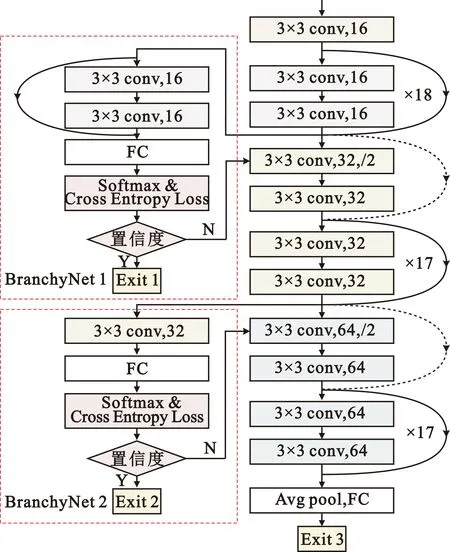
图1 B-ResNet110网络结构Fig.1 Network architecture of B-ResNet110
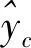
(2)
式中:zc是该出口点上全连接层的输出值。
在每一个分支的末端都有一个出口点(Exit),使用分类结果的交叉熵损失作为预测置信度的度量。如果分支1分类结果的交叉熵损失满足置信度要求,认为图像经过分支1可以进行识别,则图像在Exit 1预测结果后退出网络,不被主干网第三和第四部分处理;反之,则认为该出口点的分类结果不确定,样本继续回到网络中并在分支2的Exit 2进行预测。若Exit 2也不满足预测要求,图像将经过全部网络在Exit 3处进行预测。B-ResNet110架构可以根据输入图像的特征明显程度自适应选择主干网的层数,从而避免将所有图像逐层处理,显著减少了计算量以及正向推理时间。
B-ResNet的网络结构中包含的卷积核尺为3×3和1×1,其中3×3的卷积核步长是1和2,1×1卷积核的步长为2。池化层中池化单元的尺寸为2×2。主干网和分支网络都包含全连接层,每个分支中都包含交叉熵损失函数。对B-ResNet110而言,需要设计的硬件加速单元有通用卷积计算单元、池化计算单元、全连接层计算单元、残差结构的卷积输出加法单元,以及分支网络中提前退出机制计算单元。其中,提前退出机制包含的交叉熵损失函数较为复杂,需要根据推理阶段的实际需求对其函数进行简化。
2 硬件加速设计
2.1 定点量化设计
在FPGA中,完成不同类型的数据运算所消耗的资源和时间是不同的。表1分别列举了FPGA中16 b定点数和浮点数完成加法、减法、乘法、指数运算、对数运算所需要的DSP处理单元的个数,以及完成上述运算所需要的时钟周期。从数据中可以看出,在FPGA中定点数的运算效率以及资源利用率远大于浮点数。

表1 FPGA浮点数和定点数运算时间以及所耗资源对比Tab.1 Comparison of FPGA floating-point,fixed-point operation time and resource consumption
因此,为了使FPGA在运行神经网络时的具有更高的效率,可根据深度神经网络包含足够多的冗余信息,并且裁剪这些冗余信息不会明显导致网络准确率下降的特性,对深度神经网络权重和偏执中浮点数据类型进行16 b定点数量化,量化完成后的定点数格式如图2所示。

图2 16 b定点数格式Fig.2 Format of 16 b fixed-point number
定点数首位是1 b的符号表示位,符号位后是(15-fl)位的整数部分,最后是fl位的小数部分。因此,量化后的16 b定点数可由公式(3)表示:
(3)
2.2 卷积计算单元设计
虽然FPGA可以将卷积并行运算,但是卷积神经网络的计算量较大,将卷积层的计算在FPGA中完全展开十分困难。以B-ResNet110为例,其中主干网络的卷积层中包含的乘积累加运算(Multiply Accumulate,MAC)操作总数超过1.3亿次,单层网络所需最少MAC运算也有2.36×106次之多,这远超过适用于边缘部署的FPGA内部DSP处理单元的个数。因此,卷积神经网络部署在FPGA当中时,需要将卷积神经网络的卷积运算拆分成更小的循环,才能在FPGA的计算核心中执行。卷积计算循环分块如图3所示,卷积计算输入为N个的尺寸H×L的特征图,卷积核为M个N×K×K的三维卷积核,输出特征图的尺寸为M×R×C。将输入特征图和输出特征图按通道数、长、宽划分成Tn×Th×Tl和Tm×Tr×Tc的块,对应的卷积核被划分为Tn×Tm×K×K块。其中,Th和Tl与Tr和Tc的对应关系为Th=(Tr-1)S+K,Th=(Tc-1)S+K,S和K分别为卷积核的步长和尺寸。经过分块之后,卷积计算会从原来的4层循环转换成图3中的8层循环。这8层循环中黑色方框外部的4层循环描述的是分块数据调度方法,内部的4层表示的是FPGA计算核心中进行的分块卷积计算。

图3 卷积循环分块Fig.3 Convolutional loop partitioning
分块之后特征图与卷积核之间的卷积运算本质上来说仍是一个三维的MAC操作。每一个输入的特征图都有与之相对应的卷积核,各个特征图只与其对应的多个卷积核进行卷积运算,不同通道特征图对应卷积核之间不存在依赖关系。同通道卷积核共享输入的特征图,但这些卷积核的计算结果之间不进行累加操作,同通道的不同卷积核之间无依赖关系。因此,在计算处理单元(Processing Element,PE)阵列设计时,可以将图3红色框中的两层无依赖关系的循环并行运算,提高计算效率。
卷积计算单元的硬件设计如图4所示,由AXI Lite总线传入控制信息,AXI总线传输权重数据和特征图。卷积计算单元内部由计算模块、数据调度模块以及片上缓存组成。计算模块中的PE计算对象是输入通道分块Tn展开(Unroll)后的卷积运算,并行度为n。m个PE组成PE阵列,对输入通道不同卷积核并行展开运算,并行度为m。由图3外部循环中的循环M可以看出,每计算出一个Tm都需要循环N完整循环一次。因此,数据调度模块需要对外部数据反复进行读取,并且复用输出数据。为了减少数据传输带来的延迟,采用粗粒度流水线,即双缓存乒乓操作,对数据进行传输。这种方法可以在一组缓存中的数据参与计算的过程中,并行加载下一组输入数据以及缓存下一组输出数据。该方法既可以保证卷积计算对缓存数据乱序访问时不受输入数据影响,又可以减少数据传输的时间,从而减少访存带来的推理延迟。对于偏置权重,在第一次加载数据时与其他数据并行加载到输出缓存,将偏置值与第一次分块卷积输出结果相加。这种偏置处理方法既能代替输出缓存的复位操作从而节约复位时间,又能节省卷积运算完成后再加偏置带来的计算时间。若没有偏置,则加载数据“0”,复位输出缓存。
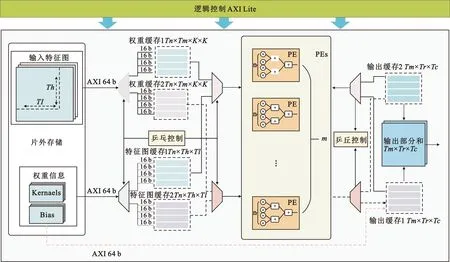
图4 卷积计算单元Fig.4 Convolutional computing unit
2.3 池化计算单元设计
池化单元的设计与卷积设计相比较为简单。池化运算单元不需要加载权重,不同特征图之间的池化计算得出的数据没有依赖关系,计算量小,输入通道数等于输出通道数,输出的部分数据不需要复用,因此池化模块只需将特征图按通道分批加载到片上计算后按序输出即可。平均池化与最大池化都采用2×2的滑窗,因此最大池化和平均池化可以复用同一个片上缓存区域从而减少资源的占用。池化单元的设计如图5所示。

图5 池化模块Fig.5 Pooling module
池化运算单元的数据输入方式与卷积运算单元一样,均由AXI总线将划分好的特征图输入并且采用粗粒度流水线减少数据传输带来的延迟。传入的特征图通过配置(config)信号,选择最大池化操作或者平均池化操作。平均操作池化首先将2×2的卷积窗的第一行的2个数据进行大小比较,存入寄存器,然后将第二行的2个数据输入进行比较,最后将两次输出结果中最大值作为最大池化操作的输出;平均池化计算将4个数据通过加法树并行相加之后取平均值。池化得出的部分结果存入输出缓存,待整张特征图计算完成后将其结果传输到片外存储。
2.4 全连接层与卷积输出加法设计
全连接层与卷积输出加法层,只涉及到顺序的加法运算和乘法运算,不需要复杂的内存访问,因此对于全连接层与卷积输出加法层,仍采用双缓存片上数据存储方式,以及粗粒度流水线加载方式。输入的数据采用加法树以及乘法器级联加法树的方法并行计算,与卷积层和池化层的设计方法相同,这里不再赘述。
2.5 提前退出模块设计实现
在动态深度神经网络中提前退出模块是核心部分,然而提前退出模块中包含的Softmax函数以及交叉熵损失函数等运算通常运用在训练时的反向传播中。该运算所包含的多次除法运算、e指数运算以及对数运算,在部署过程中会消耗大量的硬件资源并且带来过高延迟。如果用全连接层输出的最大值等指标作为置信度测量指标,虽然能减少计算量,但精度非常低,很容易造成识别结果错误。因此,可以将交叉熵损失判断置信度与全连接层的输出的最大值相结合,改进交叉熵损失函数使其更符合硬件实现的需求。
2.5.1 交叉熵函数的数学变换
公式(1)中的yc代表的标签的值,该值是“0”或“1”,并且由yc对应Softmax函数的输出决定,Softmax函数输出最大值对应的yc的标签为“1”,其他为“0”。由公式(2)可以得出,Softmax函数的输出值的大小由全连接成层的输出大小决定。因此,结合公式(1)和公式(2),在部署阶段可以用全连接层的输出值代替Softmax函数的输出值对标签值进行判断。根据判断结果,对交叉熵损失简化如公式(4)所示,因为标签为“0”的类别对应的Softmax其系数为“0”,不需要计算,所以只需要计算标签为“1”的类别对应的Softmax值,根据对数函数性质,将除法变成减法。这种变换方法可以减少C-1次Softmax运算,并且去掉所有的除法运算。该变换将较大提升推理速度。
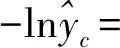
(4)
当z增加时,对z取e指数运算得出的值可能超出16 b定点数所能表示的范围,故16 b定点数并不能充分地表示该计算结果,导致计算置信度时有误差。因此,可以通过公式(5)的变换,将z取e指数运算变成z-zmax取e指数运算,将e指数运算的计算结果约束在(0,1)范围内。

(5)
由于在部署的阶段,zmax是最终的预测结果,z=zmax,因此交叉熵损失函数还可以进一步转化为公式(6)以减少计算量。
(6)
2.5.2 提前退出模块硬件实现
如图6所示,交叉熵损失函数硬件实现的过程中,充分利用FPGA可以进行并行运算的特性,将交叉熵损失函数涉及到的加法运算、比较运算并行展开,然后通过比较树以及加法树等结构将并行计算结果汇聚到一起,完成对交叉熵损失函数的加速计算。交叉熵损失函数的输出与阈值的比较结果作为提前退出的判断条件。

图6 提前退出模块Fig.6 Exit in advance module
3 设计与结果分析
3.1 实验环境
本文硬件系统设计采用的是Xilinx公司ARM+FPGA架构的 Zynq xc7z030ffg676-2芯片。搭建硬件系统时的开发环境是Vivado 2018.3和Vivado HLS 2018.3。为了与FPGA进行比较,在Inter i7-5960x CPU和NVIDIA TITAN X GPU平台上使用Ubuntu 16.04操作系统以及Chainer 5.3.0框架,实现了与FPGA完全一致的B-ResNet110模型。实验测试采用的数据集是CIFAR-10数据集。
3.2 硬件系统设计
SOC数据流如图7所示,卷积(Conv)计算单元、池化(Pool)计算单元、提前退出(Exit)计算单元、全连接层(FC)计算单元,卷积输出加法(Adder)计算单元的输入输出均通过AXI 4总线与ARM核的高速从机接口(Slave HP)相连。当SOC工作时,ARM作为主机按照B-ResNet的计算要求,通过低速主机口(Master GP)使用轻量化AXI 4总线(AXI 4 Lite)发送控制信号给各个计算单元。各个计算单元收到信号后作为主机(Master),借助Slave HP从DDR3中读取特征图信息和权重信息,计算完成后再写回到DDR3。
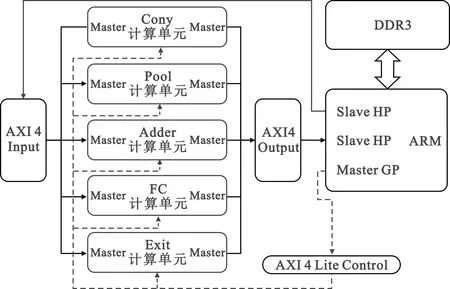
图7 SOC数据流图Fig.7 SOC data stream
根据图7所示的数据流图,在Vivado中设计搭建的SOC如图8所示。其中,计算单元中的m_axi是主机接口通过AXI连接模块(AXI SmartConnect)与AMR核的高速从机接口S_AXI_HP相连,传输数据信号,s_axi_CTRL与AMR核的M_AXI_GP相连接收控制信号。
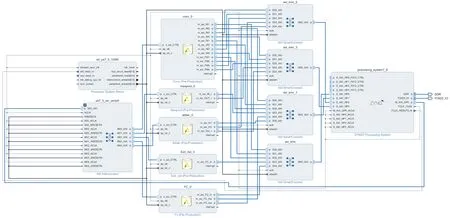
图8 SOC设计Fig.8 SOC desgin
硬件设计结果如表2所示,该SOC工作在100 MHz下,功耗为2.853 W,使用了70%左右的LUT和50%DSP的处理单元,达到了最高2.78×104MOPS(Million Operations per Second)的MAC运算,1.25 MOPS的e指数运算,以及0.125 MOPS的自然对数运算。

表2 SOC性能参数Tab.2 Performance parameters of SOC
3.3 实验过程与结果分析
神经网络模型进行定点数量化前,需要在软件端将模型权重中浮点数转化为定点数,并对比不同类型定点数对应的准确率,根据对比结果将准确率最高的定点数类型进行量化。表3给出了对神经网络在不同定点数下的准确率对比,在数据类型中用fixed

表3 量化结果对比Tab.3 Comparison of quantitative results
定点数量化后的权重将加载到外部存储DDR3,使用ARM控制FPGA中的计算IP实现B-ResNet110功能,对测试数据集进行识别。测试集图片在每个出口点的退出数量,以及每张图片的平均运行时间等由ARM统计并且通过串口传输到上位机。
表4中展示了在FPGA中实现的B-ResNet110对CIFAR-10数据集10 000张测试集的测试结果,以及CPU和GPU中B-ResNet110和ResNet110的测试结果。表中给出了网络在每个出口点输出图片的数量占测试集总数量的百分比,以及处理一张图片所用的平均时间。在退出结果误差不大的情况下,在时间方面FPGA相较于在CPU平台运行的B-ResNet110,加速比达到287%;对于CPU未加入提前退出机制的普通ResNet110,平均推理时间节省了80%。相较于NVIDIA TITAN X GPU运行的B-ResNet110,加速比达到145%;对于GPU中未加入提前退出机制的普通ResNet110,平均推理时间节省了63.9%。

表4 FPGA与CPU部署性能对比Tab.4 Comparison of FPGA and CPU deployment performance
4 结束语
本文从网络模型定点压缩,并行化、粗粒度流水线以及数学优化等角度完成了对卷积、池化、全连接和提前退出判断模块的IP设计,以及对B-Resnst-110网络的硬件实现。在Zynq xc7z030ffg676-2芯片搭建SOC系统,从消耗资源、计算能力、计算延迟等角度对硬件系统进行了分析。最终该系统获得了2.78×104MOPS的最高算力,平均帧率达到了39.12 FPS(Frame per Second)的正向推理速度,系统功耗仅为2.853 W。
动态深度网络可以有效减少不必要的计算量,减轻神经网络在边缘部署时给边缘计算平台带来的压力。未来将会继续探索其他动态网络在边缘高效部署的方法。
