无蜂窝大规模MIMO系统接入点动态选择算法*
2024-03-26裘德市
申 敏,裘德市
(重庆邮电大学 通信与信息工程学院,重庆 40065)
0 引 言
无蜂窝大规模多输入多输出(Multiple-Input Multiple-Output,MIMO)系统是文献[1]中引入的一个新概念,大量地理分布的接入点(Access Point,AP)为少量用户(User Equipment,UE)共同提供服务。每个AP通过前传链路连接到中央处理单元(Central Processing Unit,CPU),该单元主要用于信号处理。在传统蜂窝网络中小区边缘用户会受到邻近小区的干扰,而无蜂窝大规模MIMO系统通过消除蜂窝边界抑制小区间干扰,因此无蜂窝大规模MIMO系统可以为其覆盖范围的用户提供统一的服务质量。
该系统早期的设想是所有AP都为每个UE提供服务,然而这会增加CPU信号处理的计算复杂度和前传链路的负载,随着AP和UE数量的增加,使系统的可扩展性大大降低,难以实际实现。为了解决这个问题,文献[2]提出了一种以“用户为中心”的无蜂窝大规模MIMO系统,该系统中的每个UE由一组具有最佳信道条件的AP子集提供服务,不仅大大降低了前传链路的压力,并且以“用户为中心”的AP选择方案,其系统和速率和能量效率均优于全连接方案[3]。近几年来,许多文献研究了无蜂窝大规模MIMO系统AP选择算法[4-8],但是,文献[4]算法主要问题是系统和速率不是最优的;文献[5]算法未考虑每个AP服务UE的最大数量,当主AP服务的UE数量较多时,应当选择次优AP作为主AP;文献[6]算法其竞争原则是AP优先选择具有最大大尺度衰落系数的UE,若UE数量小于等于正交导频的数量时,该算法与全连接的方案一致;文献[7]算法通过连续凸优化实现AP选择,仿真结果表明具有较好的系统,计算复杂度较高;文献[8]算法在AP数量较多时预测准确率有所下降。总之,AP选择是一个全局优化问题,应当考虑系统和速率、能量效率、用户公平性等其他因素,并且能够在某些动态场景下为UE选择最佳的AP集合。
反向传播(Back Propagation,BP)神经网络是一种按误差反向传播训练的多层前馈网络,其算法称为BP算法。该算法的基本思想是梯度下降法,利用梯度搜索技术,使网络的实际输出值和期望输出值的误差均方差为最小。标准BP神经网络对初始权重的选取很敏感,可以采用一些启发式的算法(例如遗传算法)来初始化权重以提高BP神经网络的性能。
遗传算法(Genetic Algorithm,GA)是模仿自然界生物进化机制发展起来的搜索最优解的方法[9]。标准遗传算法的交叉率和变异率是固定的,这导致其搜索过程迭代慢,容易陷入局部最优。自适应遗传算法(Adaptive Genetic Algorithm,AGA)通过自适应改变交叉率和变异率,能够很好地解决这个问题。
本文提出了一种无蜂窝大规模MIMO系统AP动态选择算法,首先利用改进的自适应遗传算法为每个UE选择最佳的AP,将其作为BP神经网络的实际值;然后利用BP神经网络为不同地理位置分布的UE选择最佳的服务AP集合,BP神经网络的输入为AP和UE之间的大尺度衰落系数向量,输出为AP与UE连接关系预测向量,通过该预测向量来为用户选择最佳服务AP集合。仿真结果表明,改进的自适应遗传算法较遗传算法收敛速度更快,更不易陷入局部最优,利用改进的自适应遗传优化的BP神经网络比未优化权值的BP神经网络泛化性能更好。所提的AP动态选择算法比全连接和现有的一些AP选择算法具有更好的系统和速率。
1 系统模型
如图1所示,无蜂窝大规模MIMO系统由M个AP和K个UE组成,并且M>>K。AP和UE均匀分布在(D×D)区域内,假设所有AP和UE都配置单天线,所有AP通过前传链路链接到CPU,系统工作在时分双工(Time Diversion Duplex,TDD)模式下,即上下行信道具有互易性。每帧分为上行信道估计、下行数据传输、上行数据传输3个阶段。帧长为τc,上行训练长度为τp,上行数据传输长度为τu,下行数据传输长度为τd,并且满足τc=τp+τu+τd。
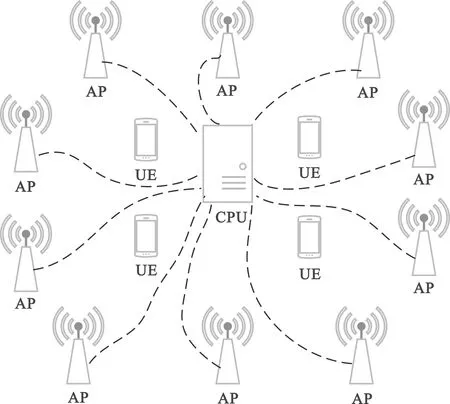
图1 无蜂窝大规模MIMO系统模型Fig.1 Cell-free massive MIMO system model
第m个AP到第k个UE之间的信道系数gm,k可表示为
(1)
式中:hm,k~CN(0,1)为小尺度衰落系数;βm,k为大尺度衰落系数,包含阴影衰落和路径损耗。路径损耗模型采用三斜率模型[10]。路径损耗为
(2)
式中:dm,k表示第m个AP到第k个UE的距离;在该路径损耗模型下,d1和d0取值分别为50 m和10 m;L的表达式为
L=46.3+33.9lg(f)-13.82lg(hAP)-
(1.1lg(f)-0.7)hUE+(1.56lg(f)-0.8)
(3)
式中:f为载波频率;hAP为AP的高度;hUE为UE的高度。
1.1 信道估计
在上行训练阶段,所有UE同时向AP发送长度为τp的导频序列,导频向量可表示为
(4)
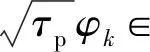
(5)
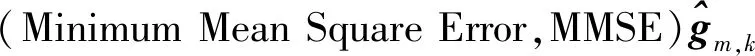
(6)
(7)
1.2 上行数据传输
在上行传输阶段,假设UE向所有AP发送载波数据符号xk(满足E{|xk|}=1),功率控制系数为ηk(满足0≤ηk≤1),则第m个AP接收到的信号为
(8)
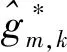
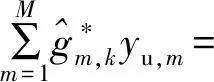
(9)
第k个UE的上行速率为
(10)
1.3 AP动态选择问题
文献[11]提出了一种无蜂窝大规模MIMO系统动态协作分簇(Dynamic Cooperation Cluster,DCC)的概念,即UE由AP的子集Mk提供服务,该子集可根据时变特征(例如UE移动性、信道时变特征)进行改变。如果全部考虑这些时变特征,算法复杂度较高,并且实现困难,所以本文只考虑在AP和UE位置随机分布的动态场景下,为UE选择最佳的服务AP子集。AP与UE的连接关系可由矩阵D∈M×K表示:
(11)
当Dm,k=1,表示UE和AP存在连接。当为全连接方案时,D为单位矩阵。
在上行数据传输阶段,通过AP动态选择后,只有部分AP向CPU传输数据,减轻了前传链路数据传输和CPU信号处理的压力。将式(11)代入到式(10),可知在AP动态选择情况下,第k个UE的上行速率表达式为
(12)
系统的上行和速率为
(13)
为了最大化系统上行和速率,则优化问题可以建模为
s.t.Dm,k∈{0,1}
(14)
式中:N为每个AP可服务的最大UE数量。
2 AP动态选择算法
为了解决AP和UE随机分布动态场景下的AP选择问题,本文设计了一个基于BP神经网络的预测模型(图2),根据AP与UE之间的大尺度衰落系数来预测AP与UE的连接关系从而最大化无蜂窝大规模MIMO系统的上行和速率。如图2所示,该模型由输入层、隐藏层、输出层组成,通过反向传播调节网络的权重和阈值来最小化均方误差[12]。
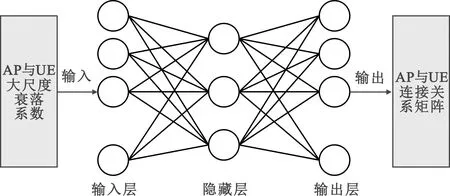
图2 BP神经网络模型Fig.2 BP neural network model
2.1 数据预处理
在无蜂窝大规模MIMO系统中,由式(2)可知,AP与UE间的大尺度衰落决定了信号的传输质量,也就是说在一定程度上能够反映AP与UE间的连接关系,因此可将AP与UE的大尺度衰落矩阵向量作为模型的输入。根据式(2)可知,大尺度衰落系数和距离成正比,会出现较大或较小的值,如果采用标准归一化,会导致部分归一化后的数据接近于0,影响BP神经网络的泛化能力(实际仿真也表明采用标准归一化的神经网络的泛化性能比采用标准差归一化的神经网络的泛化性能差),所以利用标准差对输入数据进行归一化处理:
(15)
式中:μ为输入数据的均值;σ为输入数据的方差。
BP神经网络输出层的激活函数采用sigmoid函数,误差函数为均方误差函数(Mean Square Error,MSE):
对模型中出现的符号做如下说明:L为港口群内可能开通的干线航线数;j为主干航线;M为港口群内港口数;i=1,2,3,…,M为港口;Pi为港口pi干线泊位资源数量;pi为为港口的干线泊位提供支撑的支线泊位数量;α为每单位干线泊位单位时间的处理能力;β为每单位支线泊位单位时间的处理能力;每个T0周期内直接腹地和交叉腹地的货物输出矩阵为第T周期内港口i直接腹地产生的主干航线j的货物数量,第T周期内港口i与港口i-1交叉腹地产生的主干航线j的货物数量,为第T周期内港口i与港口i+1交叉腹地产生的主干航线j的货物数量。
(16)
(17)
式中:y为BP神经网络的输出;ytrue为真实值。这两个向量转换为矩阵之后,都可以表示AP与UE的连接关系矩阵D。由式(17)可知,系统上行和速率优化问题是一个多维离散优化问题,求解难度较高。为了获得真实值,本文提出了一种改进的自适应遗传算法,简称为AGA算法。该算法由种群初始化、计算适应度、选择、交叉、变异、产生下一代种群、交叉率和变异率自适应调整变异率和交叉率等步骤组成,主要对交叉、变异、自适应调整交叉率和变异率等步骤进行了改进。由于种群中的个体采用了二进制编码,在算法迭代后期可能存在大量相似的个体,导致交叉和变异操作无效,容易陷入局部最优,于是本文对交叉和变异操作后的结果进行判断以决定是否需要重新交叉或重新变异。同时本文利用对数函数的性质来自适应改变交叉率和变异率,以提升算法的收敛速度,并且防止陷入局部最优。算法流程如图3所示。
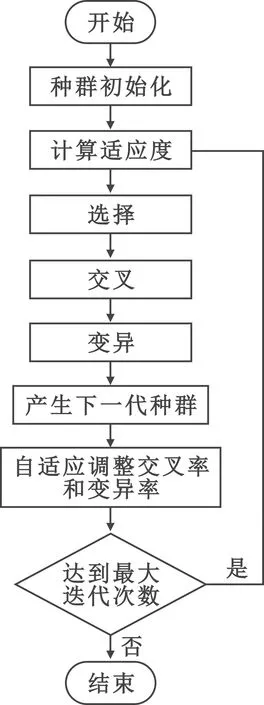
图3 改进的自适应遗传算法流程Fig.3 Improved AGA algorithm flow
算法具体步骤如下:
步骤1 种群初始化:种群中的每个个体为AP和UE之间的连接矩阵D,初始种群为Ω={D1,D2,…,DNP},NP为种群的数量。每个个体中的元素随机生成,并且需要满足每列元素不全为0。
步骤2 计算适应度:适应度为无蜂窝大规模MIMO系统的上行和速率。
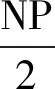
步骤4 交叉:交换两个个体相同位置的子矩阵。因为矩阵中的元素取值只有0和1,在迭代后期,可能存在许多相似的个体,所以在交叉操作之前,需要判断两个个体的子矩阵是否相同,相同则重新交叉。
步骤5 变异:随机选择个体矩阵中的一个元素,如果其值为0,则改变值为1;如果其值为1,改变其值为0。为了确保个体向最优的方向变异,计算变异后的个体适应度。如果变异后的个体适应度大于变异前的个体适应度,则认为本次变异有效,否则重新变异。
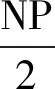
步骤7 自适应调整变异率和交叉率:本文利用对数函数的性质来自适应改变交叉率和变异率,表达式为
CrossRate=0.9-lb(1+IterN/IterSum)×0.9
(18)
VariationRate=0.1+lb(1+IterN/IterSum)×0.9
(19)
式中:CrossRate和VariationRate表示交叉率和变异率,初始值为0.9和0.1;IterN和IterSum表示当前迭代次数和总迭代次数。随着迭代次数的增加,交叉率逐渐减小,变异率逐渐增大。在迭代初期,交叉率较大,利于全局搜索最优解。在迭代后期,变异率较大,不易陷入局部最优。
BP神经网络的初始权重对网络的训练效果影响很大,随机初始化权重往往训练效果不是最佳,所以为了提高模型训练的效果,本文利用所提的改进自适应遗传算法算法优化BP神经网络的初始权重,此时每个个体为BP神经网络的权值,适应度函数为BP神经网络的均方误差,其余步骤与上述类似,不再赘述。
2.2 基于AGA-BP神经网络的AP动态选择算法
当BP神经网络训练完成后,可以代入测试输入数据。BP神经网络输出值的取值范围为[0,1],而AP与UE的连接矩阵D元素取值为0或1,所以为了得到预测输出值,需要进行转换,表达式为
(20)
此时预测输出值可以表示AP与UE之间的连接关系,代入式(13),便可以得到在预测情况下的系统上行和速率。
综上所述,本文提出的基于AGA-BP神经网络的AP动态选择算法如图4所示,具体步骤如下:
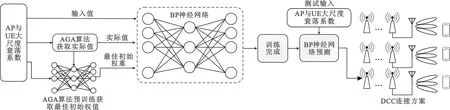
图4 基于AGA-BP神经网络的AP动态选择示意Fig.4 Schematic of AP dynamic selection based on AGA-BP neural network
1)训练阶段
步骤1 在设定的仿真环境下,随机生成不同AP与UE分布位置下的大尺度衰落系数数据,将其归一化后作为BP神经网络的输入。
步骤2 使用改进的自适应遗传算法获取BP神经网络的初始权值,使用改进的自适应遗传算法为UE选择最佳AP以作为BP神经网络的实际值。
步骤3 训练BP神经网络。
2)预测阶段
步骤1 输入归一化后的大尺度衰落数据,BP神经网络输出值并进行转换得到AP与UE的连接关系矩阵D。
步骤2 UE根据连接关系矩阵D为UE选择服务的AP。
3 仿真结果及分析
通过利用蒙特卡罗仿真对所设计的AP选择算法进行分析。考虑一个1 km×1 km的无蜂窝大规模MIMO通信区域,AP和UE的位置随机均匀分布在该区域。利用环绕技术模拟无限大的通信区域,以消除边界的影响。BP神经网络的输入层大小为M×K,隐藏层大小为2×M×K+1,输出层大小为M×K。训练数据为20 000个输入值和实际值,训练数据和验证数据分别占总数据的80%和20%,测试数据为单独生成的1 000个输入值与实际值。主要仿真参数如表1所列。

表1 仿真参数Tab.1 Simulation parameters
图5给出了当M=30,K=10时,GA算法和本文提出的改进自适应遗传算法(简称为AGA算法)的最大适应度的变化曲线,最大适应度为系统上行和速率。从图中可以看出,GA算法刚开始时的最大适应度增长较快,之后增长缓慢,可能陷入了局部最优。AGA算法在前一半的迭代过程最大适应度都增长较快,后期收敛。迭代结束后,AGA算法的最大适应度比GA算法大。这表明所提的AGA算法比GA算法收敛更快,不易陷入局部最优。
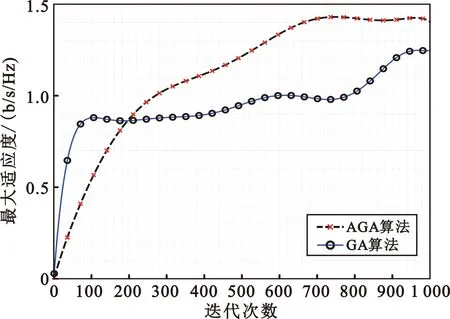
图5 GA算法和AGA算法的最大适应度随迭代次数的变化曲线Fig.5 The maximum fitness curve of GA algorithm and AGA algorithm varying with the number of iterations
图6给出了AGA-BP神经网络训练过程中训练集、验证集、测试集的误差变化曲线,可以看出随着训练次数的增加,训练集、验证集、测试集的误差慢慢降低,在训练到第988次时收敛。测试集和验证集的误差曲线基本重合,并且与训练集的误差曲线十分接近。这表明BP神经网络参数设置较为合理,训练效果较好,神经网络的泛化性能较好。
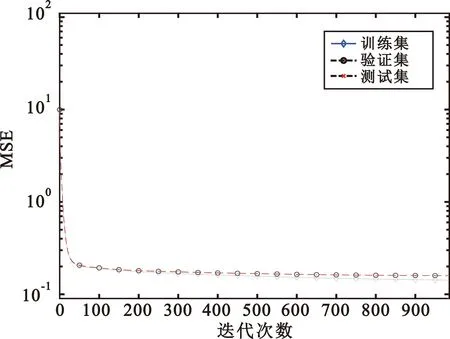
图6 AGA-BP神经网络训练的误差曲线Fig.6 The error curve of AGA-BP neural network training
图7给出了在相同神经网络参数设置,相同输入数据、测试数据、实际数据等条件下,连续训练5次神经网络,AGA-BP神经网络与BP神经网络的平均训练误差对比图。从图中可以看出,经过AGA算法初始化权重之后,神经网络的平均误差更小,AGA-BP神经网络的性能比BP神经网络好。
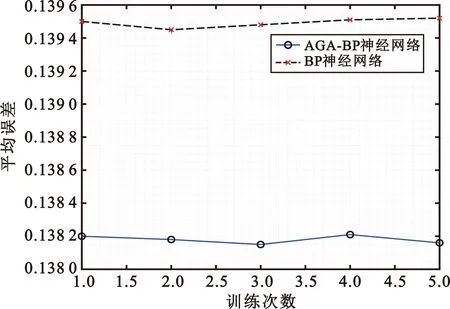
图7 AGA-BP神经网络与BP神经网络的平均训练误差曲线Fig.7 Average training error curve of AGA-BP neural network and BP neural network
图8给出了当M=30,K=10时,所提出的AP动态选择算法与其他AP选择算法的上行用户速率累计分布图。从图中可以看出,两种AP选择方案的性能比较接近,但是可扩展性方案实际使用到的AP数量小于全连接方案,这表明少量的AP也能为UE提供较好的服务质量。由于BP神经网络拟合的不完全性,动态选择方案相比较于其实际值所代表的AGA算法方案性能稍差,但是优于竞争方案和可扩展性方案。联合功率分配的AP选择方案由于其相比较与其他方案进行了功率分配,降低了UE间的干扰,理论上性能是最优的。实际仿真结果也表明该方案优于其他方案,但是其计算复杂度较高,不利于实际实现;当UE位置发生移动后,需要重新求解凸优化的解,算法的动态适应性较低。本文所提的动态选择方案,只需输入AP和UE的大尺度算法系数,通过预先训练好的BP神经网络便可为UE选择合适的AP,算法的动态适应性较好。
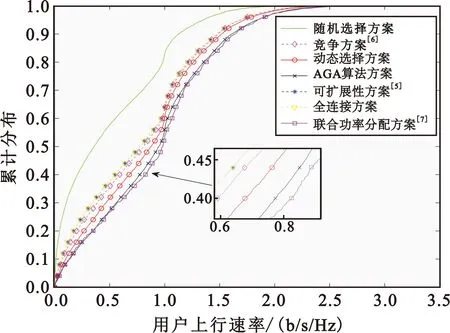
图8 不同AP选择方案的上行用户速率累计分布Fig.8 Cumulative distribution of uplink spectrum efficiency of user equipment with different AP selection schemes
4 结束语
本文针对无蜂窝大规模MIMO系统中的AP选择问题,提出了一种基于BP神经网络的AP动态选择算法。首先,利用自适应遗传算法为每个UE选择最佳的服务AP集合以最大化系统上行和速率。针对AP和UE随机分布的动态场景,利用BP神经网络来预测AP与UE之间的连接关系。BP神经网络的输入为AP与UE之间的大尺度衰落向量,输出为AP与UE之间连接关系的预测向量,并将自适应遗传算法的AP选择结果作为实际值。仿真结果表明,所提的自适应遗传算法比传统的遗传算法收敛更快,且不易陷入局部最优。BP神经网络的预测效果接近于自适应遗传算法的性能,且优于现有的一些启发式算法和全连接的方案,提升了系统的上行和速率。
在后续工作中,我们将进一步研究AP选择和功率控制的联合优化问题,进一步提升系统的能量效率。
