基于不同选样方法的雨潮遭遇风险分析
2024-03-26王尚伟刘曾美
王尚伟 刘曾美


摘要:感潮地区内涝灾害的发生同时受涝区暴雨与承泄区潮位2个致灾因子影响,在雨潮遭遇风险分析过程中,不同的选样方法将对分析结果造成影响。以中(山)珠(海)联围感潮地区为例,基于年最值选样法与超阈值选样法并结合Copula函数,对研究区雨潮遭遇风险进行分析,结果表明:①超阈值1 d降雨样本序列具有更大的样本容量,其包含更多降雨量较大的暴雨事件,同时这些较大的暴雨事件往往会与高潮位相遭遇;②由于超阈值样本序列包含了更多有效的雨潮事件数据信息,从防洪排涝规划设计的角度考虑,采用超阈值选样法得到的雨潮边缘分布更为安全,且具有更高的准确性;③基于超阈值选样法得到的雨潮联合分布具有更高的拟合优度,同时在年最值样本序列遗漏掉一些较大的暴雨信息的情况下,由超阈值样本序列计算得到的非期望雨潮组合事件发生的概率要较大一些。
关键词:雨潮遭遇;风险分析;年最值选样;超阈值选样;Copula函数;中珠联围
中图分类号:TV122文献标识码:A文章编号:1001-9235(2024)02-0105-11
Encounter Risk Analysis of Rainstorm and Tide Base on Different Sampling Method
WANG Shangwei1,LIU Zengmei2*
(1.Guangdong Hydropower Planning & Design Institute Company Limited,Guangzhou 510635,China;2.Department of Water Conservancy and Hydropower Engineering,South China University of Technology,Guangzhou 510641,China)
Abstract: Waterlogging disaster in tide-affected area usually occurs under the influence of rainstorm and tide level.In the process of risk analysis of rainstorm and tide level,different sample methods will affect the risk probability results.Taking Zhong-Zhu union catchment as an example,based on annual maximum series sampling method and peak over threshold sampling method combined with Copula function,the risk analysis results indicate that:①Sample data obtained based on peak over threshold sampling method has a larger sample size,which contains more rainstorm events than sample data obtained based on annual maximum series sampling method,and these rainstorm events tend to encounter high tide;②On the basis of containing more effective sample information,the frequency analysis results obtained by peak over threshold sampling method are more accurate and with much more security from the perspective of waterlogged drainage;③The joint distribution of rainstorm and tide based on peak over threshold sampling method showed a better fitting degree,and the probability of encountering unexpected events is larger as a result of annual maximal series sampling method omitted some effective sample information.
Keywords:encounter of rainstorm and tide;risk analysis;annual maximal series sampling method;peak over threshold sampling method;Copula function;Zhong-Zhu union catchment
在感潮地區的内涝灾害防灾、减灾安全保障体系构建过程中,往往需要通过进行雨潮遭遇风险分析以对涝区排涝布置方案和排涝设施规模进行合理确定[1-2]。雨潮遭遇风险分析关注的是与灾害系统相关,且具有自然属性的致灾因子、孕灾环境等特征值的概率分布情况,其反映的是内涝灾害发生的内在规律[3]。由于感潮地区内涝灾害的发生往往同时受涝区暴雨与承泄区潮位2个致灾因子影响,因而内涝灾害防治中需要进行涝区暴雨与承泄区水位2个致灾因子的遭遇风险分析[4]。如今在雨潮、雨洪及洪潮等水文变量的遭遇风险分析中,Copula函数因其能够灵活构造边缘分布为任意形式的多变量之间的联合分布而得到了广泛的应用。刘曾美等[5]基于Copula函数研究了中山市坦洲镇涝区的暴雨和相应承泄区潮水位的联合分布,研究了涝区暴雨与承泄区水位遭遇组合的涝灾风险;刘曾美等[6]也分别采用定性分析法和基于Copula函数的概率风险分析法对中珠联围暴雨与上游西江洪水的雨洪遭遇规律进行了探究;石赟赟等[7]基于Copula函数构建了深圳市年最大1 d降雨量与相应潮位的联合分布,对不同雨潮遭遇情景对应的概率进行了计算分析;周焕等[8]在浙江省多个沿海流域的防洪排涝规划设计中对基于Copula函数的雨潮遭遇风险分析成果进行了验证,结果表明该方法分析成果较传统的雨潮组合定性分析方法分析成果具有较强的可靠性和实用性;Xu等[9]为了探究台风对雨潮遭遇风险的影响,基于Copula函数构建了海南省海口市暴雨、台风和风暴潮的三变量联合分布;Bouchra Zellou等[10]基于Copula函数构建了摩洛哥Bouregreg河口区域的雨潮遭遇风险模型,并对该区域发生内涝灾害事件的概率进行了预测分析;王保华等[11]将基于Copula函数的洪潮遭遇分析模型应用于海南省五源河流域治理工程中,对与工程建设规模等级相匹配的洪潮组合设计值进行了合理确定。
尽管目前基于Copula函数的多水文变量遭遇风险研究已有较多典型案例,但大多数并未考虑到其中选样方法可能对分析结果造成的影响,在水文变量频率分析中大多仅考虑采用一般常用的年最值选样法。由年最值选样法得到的样本序列能够保证样本之间的独立性,但在资料年限较短的情况下,得到的样本序列容量小,往往具有较大的抽样误差,且容易遗漏掉一些较大的次大值样本信息[12]。与年最值选样法相比,超阈值选样法则以超过特定阈值为取样前提,可以扩大样本容量,使有限的资料信息得到充分的利用。因此,本次研究选择以中(山)珠(海)联围感潮地区为例,考虑采用年最值选样与超阈值选样两种不同的选样方法,并结合Copula函数对研究区雨潮遭遇风险进行分析,对比不同选样方法对雨潮边缘分布、雨潮联合分布及雨潮遭遇风险造成的差异影响,并为感潮地区涝区排涝布置方案和排涝设施规模的确定提供参考依据。
1 研究区概况
中(山)珠(海)联围位于珠江三角洲下游,片区横跨广东省中山市和珠海市,东南与澳门半岛相邻,隔磨刀门水道与珠海市斗门区相望,北接五桂山脉和凤凰山脉,地势东北向西南倾斜。由于中珠联围自身特殊的地理位置和地形条件,其境内降雨频繁,且往往具有强度大、雨量多的特点;磨刀门水道为中珠联围集水片区主要的承泄区,属感潮河段,其水位既受自下而上的河口潮波的影响,又受自上而下的西江洪水径流的作用。大量历史资料表明,当中珠联围片区内较大的暴雨遭遇承泄区被整体抬高的潮位时,河口水闸自排受到阻碍,导致片区内的积水无法及时排除,因而极易形成涝灾[13]。为合理确定涝区排涝布置方案和排涝设施的规模,在实际的防洪排涝规划设计过程中,必须对片区内的雨潮遭遇风险规律进行重点研究。
本次研究中,受资料条件限制,雨量数据选择采用位于中山市三乡镇的三乡雨量站,位于中山市神湾镇的神湾雨量站、位于珠海市香洲区的竹仙洞雨量站共3个雨量站(图1)的日降雨量观测数据,并通过加权平均得到集水片区的逐日面雨量,样本数据时间序列为1973—2008年(缺失1986、1987、2000年)共33 a;潮位数据选择采用位于磨刀门水道的灯笼山潮位站逐日潮位观测数据。
2 雨潮边缘分布频率分析
对于暴雨内涝灾害而言,涝区受灾的根本原因仍在于涝区内发生的极端降雨,承泄区潮位则主要作为与河口洪水遭遇的可变化的相应边界条件对涝水外排造成影响[5]。因此,本次研究选择采用以暴雨为主,潮位相应的雨潮组合方式,即分别采用年最值选样法和超阈值选样法对1 d雨量样本数据进行选样,并在潮位样本数据中按当日不规则半日潮的高高潮选取相应潮位。
2.1 年最值选样法
年最值选样法选取每年的最值一个样本组成序列进行频率分析,年最值样本序列的经验频率按式(1)计算:
式中 Pm——经验频率;N——选取的样本序列总数;m——各样本由大到小排列的序号。
本次研究采用水文计算规范中指定采用的P-Ⅲ型分布线型对年最值1 d降雨序列进行拟合,其分布函数为式(2):
式中 α——形状参数,α>0;β——尺度参数;γ——位置参数;Γ(α)——α的Gamma函数。
考虑到相应潮位分布线型接近负偏态,采用可适用于描述负偏态线型的广义极值分布线型对相应潮位序列进行拟合,其分布函数为式(3):
式中 μ——位置参数;α——尺度参数,α>0;k——形状参数,k≠0。
参数估计方法采用具有无偏性的线性矩法[15],并采用概率点据相关系数法(PPCC)与四阶线性矩检验法(TW4)[16]进行拟合优选,频率分布曲线见图2、3,频率分布参数见表1。
2.2 超阈值选样法
超阈值选样法以每年中超过阈值的观测数据来共同组成样本序列进行频率分析,该方法选样得到的超阈值序列由大到小排列得到的频率为一年发生多次的次频率,需要转换为实际应用中的年频率,超阈值样本序列的年频率按式(4)计算:
式中 PE——年频率;N——选取的样本序列总数;m——各样本由大到小排列的序号;k——每年平均取样个数。
由超阈值选样法得到样本序列服从广义Pareto分布,其分布函数为式(5)、(6):
式中 a——形状参数;b——尺度参数,b>0;x0——阈值。
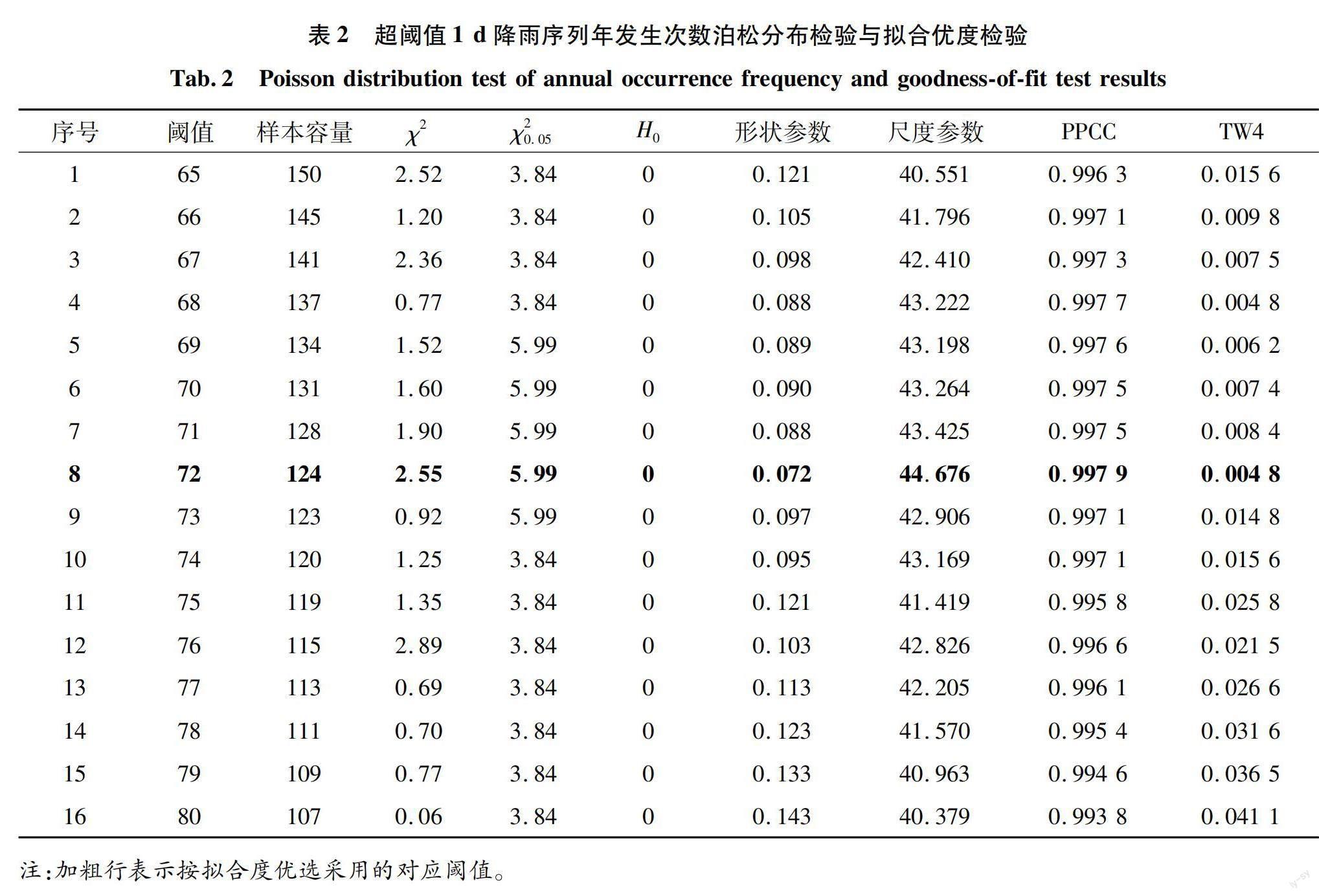
在超阈值选样法中,阈值的选取对频率分析结果有着很大的影响。如果选取的阈值偏小,则不能保证超限量分布的收敛性,使参数估计产生大的偏差;如果选取的阈值偏大,则可能导致超限数据的样本序列数量较少,使得一些有用的资料信息被浪费,造成估计的分布参数偏差较大[18]。本次研究通过以下几个步骤确定选样阈值。
a)分析雨量资料的数据特性。根据中珠聯围境内及周边雨量站所有雨量观测资料,降雨量年最大1 d雨量的最小值为72.7 mm,阈值的选取范围可初步确定为65~80 mm,按公差为1.0 mm构成16个超阈值1 d降雨序列。
b)年发生次数的泊松分布检验。对于满足广义Pareto分布的超阈值序列,其年超限数,即超过阈值的年发生次数,应服从泊松分布。对于选取的16个超阈值1 d暴雨序列,在显著水平0.05下进行χ2检验(原假设H0=0表示符合泊松分布)。检验结果见表2,16个超阈值序列的年超限数均符合泊松分布。
c)拟合优度检验。对16个超阈值1 d暴雨序列采用广义Pareto分布进行拟合,参数估计方法采用概率权重矩法。采用PPCC法和TW4法对16个超阈值1 d暴雨序列的频率分布进行拟合优度评价,各超阈值序列的拟合优度见表2。
根据检验结果可知,当阈值选取为72 mm时拟合度最优,因此最终选取72 mm作为对降雨数据进行超阈值选样的阈值,其广义Pareto分布参数见表3,频率分布曲线见图4。
确定阈值之后,根据得到的超阈值1 d降雨序列在潮位样本数据选取相应潮位得到超阈值相应潮位序列,采用广义极值分布线型对相应潮位序列进行拟合,得到的频率分布参数见表3,频率分布曲线见图5。
3 雨潮联合分布频率分析
在雨潮单变量边缘分布已经确定的基础上,选择借助Copula函数对雨潮变量之间的相关性结构进行描述。设F(h,z)为中珠联围1 d降雨量随机变量H和承泄区感潮河段相应潮位随机变量Z的联合分布函数,其边缘分布为FH(h)和FZ(z),根据Sklar定理,一定存在唯一的Copula函数C(u,v),使得:
F(h,z)=C[FH(h),FZ(z)] (7)
目前,在水文变量频率分析中采用Archimedean Copula函数已具有较为成熟的理论和应用基础,其主要包括GH Copula函数、Clayton Copula函数、AMH Copula函数和Frank Copula函数4种函数[19],对应的联合分布参数θ可根据雨潮序列之间的Kendall秩相关系数τ确定,见表4。
Kendall秩相关系数是常用于度量水文变量相关性的指标,其定义如下:
式中 (x1i,x2i)——观测点据;sign(·)——符号函数,当(x1i-x1j)(x2i-x2j)>0时,sign=1,当(x1i-x1j)(x2i-x2j)<0时,sign=-1,当(x1i-x1j)(x2i-x2j)=0时,sign=0。
将年最值选样法得到的年最大1 d降雨序列与相应潮位序列、超阈值法得到的超阈值1 d降雨序列与相应潮位序列分别构建雨潮联合分布,得到的雨潮联合分布参数见表5。采用AIC信息准则法(AIC)和离差平方和最小准则(OLS)对得到的联合分布进行拟合优度评价,结果表明:对于由年最值选样法得到的降雨序列与相应潮位序列,在采用Clayton Copula函数构建雨潮联合分布时达到最佳的拟合效果;对于由超阈值选样法得到的降雨序列与相应潮位序列,在采用GH Copula函数构建雨潮联合分布时达到最佳的拟合效果,雨潮联合分布最优拟合度情况见图6、7。
4 雨潮遭遇风险分析
在雨潮遭遇风险分析中,降雨量和潮位均属于变量值越大越不利的水文变量,当降雨量或潮位超过某个设定值时,通常将其称为非期望事件,可以通过不同风险率的计算对各种情景对应发生的不确定性进行分析[20]。
从灾害成因的角度来分析,内涝灾害的2个最主要致灾因子是暴雨H与潮位Z;显然当涝区暴雨超过设计值时,涝区将会遭受内涝灾害,同时即使涝区暴雨未超过设计标准,但承泄区潮位超过与设计暴雨相组合的设计潮位值时,涝区还是会发生内涝,即暴雨H与潮位Z之中一个变量超过设计值时涝区就会发生内涝,对应的风险率即为联合风险率,反映了涝区可能遭受内涝灾害的概率,见式(9)[20]:
PLH=P[(H>h)∪(Z>z)]=1-P[(H 其次,从内涝灾害最不利的情况来考虑,即涝区暴雨与承泄区潮位同时超过设计值的情况,对应的风险率即为同现风险率,反映了内涝灾害最大情况发生的概率,见式(10): PTX=P[(H>h)∩(Z>z)]=P(H>h)+P(Z>z)-[1-P[(H 將以上频率分析得到的雨潮边缘分布与联合分布代入风险率计算公式中,可得到中珠联围雨潮遭遇风险见表6、7。 5 结果与分析 5.1 雨潮统计特征 本次研究采用年最值选样法共得到雨潮样本33组,采用超阈值选样法共得到雨潮样本124组,相对比超阈值样本序列具有更大的样本容量。雨潮样本序列基本统计特征见图8、9,在每个箱子上,红色实线表示中位数,箱子的底边和顶边分别表示第25个和75个百分位数,须线会延伸到不是离群值的最远端数据点,离群值是距离箱子底部或顶部超过1.5倍四分位差的值,离群值使用“+”标记符号单独绘制。据图8显示,年最值1 d降雨样本序列中位值为161.2 mm,所有样本值均落在正常值范围内,没有出现离群值;超阈值1 d降雨样本序列中位值为99.4 m,较年最值样本序列明显减小,同时出现较多高于箱子上边界的离群值,其反映出研究区年内往往会遭遇多次强降雨,并且其中存在较多降雨量与年最值降雨接近的次大值降雨。同时据图9显示,年最值相应潮位样本序列中位值为1.15 m,与年最值1 d降雨样本序列统计特征保持一致,所有样本值均落在正常值范围内,没有出现离群值;超阈值相应潮位样本序列中位值为0.94 m,较年最值样本序列略有减小,离群值大多出现于箱子上边界以外的区域。此外,从图10中可以明显发现,年最值1 d降雨样本序列由每年最大值一个样本组成系列,其相应潮位样本序列每年仅包含一个样本值,超阈值1 d降雨样本序列则由超过阈值(72 mm)的最值与次大值组成,其中部分次大值降雨遭遇的相应潮位要高于年最值降雨遭遇的相应潮位。 总体而言,超阈值1 d降雨样本序列具有更大的样本容量,其包含更多降雨量较大的暴雨事件,同时这些较大的暴雨事件往往会与高潮位相遭遇。 5.2 雨潮边缘分布特征 基于年最值选样法与超阈值选样法得到的雨潮邊缘分布频率分析结果见表8,各重现期对应的雨潮变量设计值见图11、12。结果表明,在重现期小于50年一遇时,2种选样方法的暴雨设计值相差不大,但在重现期大于50年一遇时,超阈值选样法得到的暴雨设计值明显大于年最值选样法得到的暴雨设计值,且两者之间的差值随着重现期的增大而增大;相应潮位设计值则存在更为显著的差异,超阈值选样法得到的相应潮位设计值均大于年最值选样法得到的相应潮位设计值。 同时,在综合考虑PPCC与TW4两种拟合优度评价指标的情况下,对于1 d降雨边缘分布,基于年最值选样法频率分析得到的最优拟合度分别为0.996 4和0.027 5,基于超阈值选样法频率分析得到的最优拟合度分别为0.997 9和0.004 8;对于相应潮位边缘分布,基于年最值选样法频率分析得到的最优拟合度分别为0.980 8和0.024 2,基于超阈值选样法频率分析得到的最优拟合度分别为0.996 3和0.002 0;可以发现,基于超阈值选样法得到的雨潮边缘分布拟合度指标均优于基于年最值选样法得到的。 综上分析,由于超阈值选样法选取的样本包含了更多有效的雨潮事件数据信息,从防洪排涝规划设计的角度考虑,采用超阈值选样法得到的雨潮边缘分布更为安全,且具有更高的准确性。 5.3 雨潮联合分布与风险率特征 根据表5中的结果,年最值选样法得到的年最大1 d降雨序列与相应潮位的Kendall秩相关系数为0.014;大于超阈值选样法得到的年最大1 d降雨序列与相应潮位的Kendall秩相关系数为0.197;即超阈值选样法得到的1 d降雨序列与相应潮位序列具有更强的相关性。同时,在综合考虑AIC与OLS 2种拟合优度评价指标的情况下,基于年最值选样法频率分析得到的最优拟合度分别为-192.01和0.004 825,基于超阈值选样法频率分析得到的最优拟合度分别为-910.02和0.002 916,可以发现,基于超阈值选样法得到的雨潮联合分布拟合度指标均优于基于年最值选样法。 根据表6、7中的结果,可以发现,年最值选样法得到的同现风险率、联合风险率结果均小于超阈值选样法得到的结果,与文献[21]中的研究结论一致。例如,在基于年最值选样法的情况下,中珠联围20年一遇年最大1 d降雨与相当于5年一遇年最高潮位的感潮河段相应潮位组合时,同现风险率、联合风险率分别为0.04%、5.66%;在基于超阈值选样法的情况下,中珠联围20年一遇年最大1 d降雨与相当于5年一遇年最高潮位的感潮河段相应潮位组合时,同现风险率、联合风险率分别为0.36%、9.67%,后者得到的风险率要大于前者;同样,在其他不同的雨潮组合情况下可以得到相同的结论。进一步分析认为,造成这一差异变化的主要原因为相较于年最值选样,超阈值选样不仅仅选取每年的最大降雨量作为样本数据,还选取了小于年最大降雨量,同时大于阈值的次大值降雨量,而这些次大值多数只是略小于年最大值,因此在年最值样本序列中遗漏掉了一些较大的暴雨信息,也就遗漏了其相应潮位信息,从而导致年最大值选样的样本序列计算得到的非期望雨潮组合事件发生的概率较超阈值样本序列计算的要小一些。 6 结语 本文以位于感潮地区的中(山)珠(海)联围为例,分别采用年最大值选样法与超阈值选样法进行了涝区暴雨与承泄区潮水位的遭遇风险分析。年最大值选样法遗漏掉了一些较大的暴雨信息,而超阈值选样法则充分利用了这些雨量较大的暴雨事件,且因这些较大的暴雨事件往往可能会与较高的潮位相遭遇,因而基于超阈值选样法比基于年最大值选样法分析得到的非期望雨潮组合事件发生的概率要大,且基于超阈值选样法进行雨潮遭遇分析能客观地揭示涝区暴雨与承泄区水位的遭遇规律。因此,若资料条件许可,在内涝灾害防治规划设计中建议采用超阈值选样法进行雨洪遭遇分析。 参考文献: [1]刘曾美,吴俊校,肖素芬. 感潮地区排涝分析计算方法和思路研究[J].人民珠江,2009(5):8-11,46. [2]刘曾美,陈子燊. 区间暴雨和外江洪水位遭遇组合的风险[J].水科学进展,2009(5):619-625. [3]刘曾美,陈子燊,吴俊校. 变化环境下治涝效益估算方法研究[J].水利学报,2011,42(9):1081-1087. [4]刘曾美,陈子燊. 基于两个致灾因子的治涝标准研究[J].水力发电学报,2011,30(3):39-44,49. [5]刘曾美,吴俊校,陈子燊. 感潮地区暴雨和潮水位遭遇组合的涝灾风险[J].武汉大学学报(工学版),2010(2):166-169,174. [6]刘曾美,王尚伟,蔡玉婷,等.感潮地区涝区暴雨与承泄区上游洪水的遭遇规律[J].水资源保护,2021,37(2):89-94,107. [7]石赟赟,姚航斌,万东辉,等.基于Copula函数的深圳市雨潮遭遇风险分析[J].人民珠江,2021,42(12):24-29,41. [8]周焕,揭梦璇.基于Copula函数的浙江沿海流域雨潮组合风险分析[J].人民长江,2019,50(4):32-35,85. [9]XU H S,XU K,BIN L L,et al. Joint Risk of Rainfall and Storm Surges during Typhoons in a Coastal City of Haidian Island, China[J]. International Journal of Environmental Research and Public Health,2018,15(7).DOI:10.3390/ijerph15071377. [10]BOUCHRA Z,HASSANE R.Assessment of the joint impact of extreme rainfall and storm surge on the risk of flooding in a coastal area[J].Journal of Hydrology,2018,569.DOI:10.1016/j.jhydrol.2018.12.028. [11]王保華,王占海,月永昌.Copula函数在洪潮遭遇分析中的应用研究[J].人民珠江,2015,36(5):62-65. [12]蓝福鹏.不同选样方法的市政排水与水利排涝暴雨标准衔接关系对比研究[D].广州:华南理工大学,2020. [13]刘曾美.中山市坦洲镇水利规划[R].广州:华南理工大学,2014. [14]刘曾美,覃光华,陈子燊,等.感潮河段水位与上游洪水和河口潮位的关联性研究[J].水利学报,2013,44(11):1278-1285. [15]HOSKING J R M, WALLIS J R. Regional Frequency Analysis[M]. Cambridge:Cambridge University Press,1997. [16]梁骏. 水文设计值置信区间计算方法研究[D].杨凌:西北农林科技大学,2016. [17]李兴凯,陈元芳.暴雨频率分布线型优选方法的研究[J].水文,2010,30(2):50-53. [18]陈子燊,刘曾美,路剑飞.基于广义Pareto分布的洪水频率分析[J].水力发电学报,2013,32(2):68-73,83. [19]郭生练,闫宝伟,肖义,等. Copula 函数在多变量水文分析计算中的应用及研究进展 [J].水文,2008,28(3) :1-7. [20]刘曾美.极值分布理论与风险分析在珠江三角洲水灾害中的应用[D].广州:中山大学,2011. [21]涂新军,杜奕良,陈晓宏,等.滨海城市雨潮遭遇联合分布模拟与设计[J].水科学进展,2017,28(1):49-58. (责任编辑:李泽华)
