基于时间序列与CNN-GRU的滑坡位移预测模型研究
2024-03-26符振涛李丽敏王莲霞任瑞斌崔成涛封青青
符振涛 李丽敏 王莲霞 任瑞斌 崔成涛 封青青

摘要:滑坡位移预测是滑坡预警的重要依据之一。针对以往预测模型在预测精度上存在的不足,提出了一种基于时间序列与卷积门控循环单元(CNN-GRU)的滑坡位移动态预測模型。首先,利用小波分析确定存在趋势项位移后,利用指数平滑法对累计位移分解得到趋势项与周期项位移,将趋势项采用五次多项式拟合;之后,采用自相关函数检验位移的周期特征,利用灰色关联法判断各因子与周期项之间的关联度,并将周期项与影响因子一起输入CNN-GRU模型进行预测;最终,叠加得到累计位移预测值。以三峡库区白水河滑坡为例,选取2004年1月至2012年12月数据进行研究,最终预测结果平均绝对误差百分比仅为0.525%,RMSE为9.614、R2为0.993。试验结果表明,CNN-GRU具有更高的预测精度。
关键词:位移预测;时间序列;卷积门控循环单元;白水河滑坡
中图分类号:X43文献标识码:A文章编号:1001-9235(2024)02-0001-08
Landslide Displacement Prediction Model Based on Time Series and CNN-GRU
FU Zhentao,LI Limin,WANG Lianxia,REN Ruibin,CUI Chengtao,FENG Qingqing
(School of Electronics and Information,Xian Polytechnic University,Xian 710600,China)
Abstract:Landslide displacement prediction is an important basis for early landslide warning.This paper proposes a prediction model of landslide moving states based on time series and convolutional gated recurrent unit (CNN-GRU) to deal with the shortcomings of previous prediction models.Firstly,after employing wavelet analysis to determine the displacement of the trend term,the exponential smoothing method is adopted to decompose the cumulative displacement to obtain two displacement types of the trend term and the periodic term,and the trend term is fitted by a five-order polynomial.Then,the autocorrelation function is utilized to test the periodic displacement characteristics,and the gray correlation method is applied to determine the correlation degree between each factor and the periodic term.Meanwhile,the periodic term and the influencing factor are input into the CNN-GRU model for prediction,and finally the predicted cumulative displacement value is obtained by superposition.By taking the Baishui River landslide in the Three Gorges Reservoir area as an example,this paper selects the data from January 2004 to December 2012 for study,and the average absolute error percentage of the final prediction results is only 0.525%,with RMSE of 9.614 and R2of 0.993.Experimental results show that CNN-GRU has higher prediction accuracy.
Keywords:displacement prediction;time series;convolutional gated recurrent unit;Baishui River landslide
滑坡是常见的自然灾害之一,据国家统计局报告,2021年中国发生滑坡灾害2 335起,占全年地质灾害总数的48.9%,造成直接经济损失数十亿,因此通过历史地质数据综合判断滑坡的演变工程,并对滑坡的变化趋势做出预测成了防灾减灾的必要手段。
时间序列分解方法以其完善的理论获得广大学者的青睐。在趋势项的分解上,杨背背等[1]应用移动平均法,将白水河滑坡累积位移分解为周期项和趋势项。黄海峰等[2]使用平滑先验法分离了趋势项位移,对白家包滑坡进行了预测,以上方法虽然取得了一定成果,但分离的趋势项中仍然具有周期项的阶跃特征,导致最终预测结果误差较大。本文采用指数平滑法对实验区累计位移进行多次分解,将最后一次分解的结果作为趋势项,克服了传统方法在阶跃变化时分解得到的趋势项仍具有明显周期性的问题。
在周期项的预测上,鄢好等[3]、宋丽伟[4]分别将循环神经网络(RNN)改进的门控循环单元(GRU)与长短时记忆网络(LSTM)引入滑坡位移预测,以上网络通过增加“门”解决了RNN网络梯度爆炸的问题,可以实现位移预测,但是考虑了滑坡变形的动态演化过程,单一网络不能同时满足特征提取与趋势学习,导致其预测误差较大,亟待改进。滑坡位移的数据具有连续性、周期性[5]等特点,CNN神经网络能够自动发现并提取输入数据的波形特证[6]。GRU神经网络可以通过更新门和遗忘门实现对数据变化趋势的学习[7],因此,本文将CNN-GRU网络模型引入位移预测领域,提出基于CNN-GRU的滑坡位移预测方法。
本文以白水河滑坡为研究区,首先,利用小波分析确定存在趋势项位移后,使用指数平滑法分解累计位移,对于趋势项位移本文采用五次多项式进行拟合,得到趋势项预测值;随后,采用自相关函数检验位移的周期特征,引入灰色关联度法量化影响因子与周期项位移间的相关性,保留具有较高关联度的影响因子;之后,选择CNN-GRU神经网络进行周期项预测。将该结果和GRU、LSTM和CNN-LSTM预测结果一同与真实值作对比,从而验证本文所使用模型的准确性。最后将周期项与趋势项叠加得到累计位移预测值,并利用均方根误差、平均绝对百分比误差等评价方法分析计算预测精度。
1 滑坡位移预测模型
1.1 位移序列检验
a)趋势项检验。小波变换是一种信号分析方法,它可以将信号分解成不同尺度的成分,从而更好地理解信号的频率和时间特性。与傅里叶变换不同,小波变换可以同时提供时间和频率信息,可以将信号分解成不同频率的子信号,因此在处理非平稳信号时更为有效,见式(1):
式中 α——尺度,控制小波函数的伸缩;τ——平移量,控制小波函数的平移。
在累计位移中,趋势项通常对应着低频信号,如果存在趋势项位移,那么整个信号的低频部分会发生变化,因此可以通过小波变换检验是否存在趋势项位移。
b)周期项检验。自相关函数(autocorrelation function)是一种用于衡量时间序列中自身相关性的统计量,是信号在时域中的平均度量,它用來描述随机信号x(t)在任意2个不同时刻s、t的取值之间的相关程度,分析自相关函数值即可得到时间序列数据的是否存在周期项,见式(2):
式中 r(k)——自相关系数;cov(Xt,X{t-k})——Xt、X{t-k}之间的协方差;std(Xt)、std(X{t-k})——Xt和X{t-k}的标准差。
1.2 位移时间序列分解
滑坡位移按时间序列分解理论可分解为趋势项位移与周期项位移[8],滑坡位移时间序列模型见式(3):
y(t)=ω(t)+c(t) (3)
式中 y(t)——累计总位移;ω(t)——趋势项位移;c(t)——周期项位移。
由于研究区坡体不同年份阶跃幅度变化较大,采用传统方法得的趋势项位移曲线仍具有明显的周期特点,为了解决这个问题,本文引入指数平滑法对累计位移进行分解,将多次分解后的结果作为最终的趋势项。
指数平滑法是一种特殊的加权平均法,其基本原理为对t期真实值和t-1期平滑值赋予不同的权重,从而求得当前平滑值的方法[9]。指数平滑法基本原理为:
St=ayt+(1-a)St-1(4)
式中 St——第t期的趋势项;yt——第t期真实值;St-1——第t-1期平滑值;a——平滑指数。
由式(4)可知,当a越接近1时,第t期平滑结果越接近第t期观察值。
1.3 CNN算法
CNN网络是一种深度学习模型,由于其具有局部区域连接、权值共享、降采样的结构特点,使得其在图像处理领域具有独特的表现,并获得了广泛应用[10]。本文针对位移数据建立了一维卷积神经网络。CNN通过卷积核实现特征提取,具体步骤如下,首先初始化一个特征向量集M,然后在反向传播中循环更新这个集合,让其不断逼近真实解,从而实现对位移数据的特征F的提取。一维卷积计算见式(5):
式中 xl-1J——l-1层第j个输出;f——激活函数;wlij——卷积核的权重矩阵;xlj——l层第j个输出;blj——偏置项。
1.4 GRU算法
GRU(Gate Recurrent Unit,门控循环单元)是为了解决RNN梯度爆炸问题[11]而提出来的一种循环神经网络。GRU模型在RNN基础上引入了2个门:更新门和重置门。结构见图1。
图中的zt和rt分别表示更新门和重置门。其数学表达式为:
式中 ωr——重置门的权重;ωz——更新门的权重;tanh——双曲正切函数;σ——sigmoid函数。
其中ωz、ωr、和ω0为需要训练的参数。
1.5 CNN-GRU算法
滑坡位移数据在时间序列上具有连续性及周期性,单独使用GRU神经网络时,通过构建多个GRU单元虽然可以学习位移数据的变化趋势,从而实现位移预测,但无法提取位移数据特征导致结果出现较大误差。因此本文提出将CNN-GRU组合网络应用于滑坡周期项位移预测中,首先通过CNN网络提取输入特征,构建时序性的特征向量,并将结果输入到GRU模型中学习这些特征的时间变化趋势[12],从而实现对滑坡位移的预测。
网络结构见图2。CNN部分本文设计了2层一维卷积层,卷积核数目分别为4、8,每次卷积后都对应一次最大池化,选取ReLU作为激活函数。在经过2次卷积、池化、扁平处理后,得到一维全局特征向量并将其作为GRU层的输入,经过全连接层后输出预测结果。将CNN与GRU相结合可以实现对位移数据时空特征的完整学习。
1.6 模型精度评价
本文采用均方根误差(Root Mean Square Error,RMSE)、平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)、决定系数(R-Square,R2)[13]以及绝对误差指标评估模型预测精度。
2 白水河滑坡概况
2.1 工程地质概况
白水河滑坡地处湖北省秭归县,距离三峡大坝56 km,属于三峡库区范围。滑坡前缘没入长江;左右两侧以基岩山脊为界[14];后缘以岩土分界处为界。滑坡主滑方向约为 NE20°,NS向长约 600 m,EW向宽约700 m,平均厚度30 m,体积约1.26×107m3,属大型堆积层滑坡[15]。白水河滑坡历史上已发生多次较大的变形。2005年8月至2006年8月,滑坡地表多处出现下沉拉裂缝。2007年6月30日,预警区后缘发生较大规模坍塌。2009年8月,滑坡西部邊界裂缝呈羽状断续扩展。
2.2 滑坡特征分析
白水河滑坡平面见图3,本文选取白水河滑坡区ZG118监测点数据进行研究。
通过整理实验区自2004年1月至2012年12月的降雨量和库水位数据,分别得到滑坡位移变化与库水位、降雨量的关系见图4、5,图4显示白水河滑坡在库水位减少后往往会发生阶跃性增长,如2008年12月至2009年8月,库水位由170.5 m减少至152.8 m,位移由828.4 mm增加至1 072.8 mm。白水河滑坡变形也受降雨的影响,见图5。每年6—9月为汛期,汛期时因为降雨渗入土壤,会破坏坡体水-土力学平衡[15],导致发生阶跃性增长。
3 滑坡位移预测
3.1 趋势项位移检验
小波分解中,信号被分解成多个子信号,每个子信号对应着不同频率的成分。小波系数反映了每个子信号中不同频率成分的能量大小,可以用来描述信号的频率特征。如果小波系数在高尺度上较大,而在低尺度上较小,则说明存在趋势项,依据式(1)编写程序,计算各个尺度下的小波系数。第四层小波系数的最大值要大于低层小波系数最大值,故可知存在趋势项位移,见图6。
3.2 趋势项提取及预测
本文取2004年1月至2012年12月的滑坡位移数据作为原始数据。由于需要取前12月位移均值作为平滑初值,在此步骤使用了2004年1月至2006年12月的数据,最终得到的趋势项时间范围为2007年1月至2012年12月。
3.2.1 指数平滑法
为了解决传统方法提取的趋势项仍然具有明显周期性特点的问题,本文采用指数平滑法提取趋势项位移,该方法分解结果由α取值决定,α的取值范围为0~1,取值趋近于1时,平滑曲线与真实值越接近,曲线趋近于0时,曲线越接近直线。
不同α取值结果见图7。测试中当α大于0.5后虽然趋势项曲线更加平滑,但会失去滑坡位移特征。当α小于0.3时,得到的趋势项位移中仍然具有周期项特征。所以,当α处于0.3~0.5时,分解效果最好。
指数平滑法使用次数越多,得到的曲线越平滑,但最终预测精度会受到影响。综合考虑分解效果和预测精度,取α=0.35,平滑次数为3次。
趋势项提取结果见图8。只使用1次平滑时结果具有明显的阶跃变化,此时结果仍然具有周期性特征。重复使用3次平滑后,去除了累计位移中的周期性特征部分,取此结果作为趋势项位移。
3.2.2 趋势项位移预测
将分解得到的趋势性位移的各时段数据进行五次多项式拟合,拟合计算式为:
y=a1x5+a2x4+a3x3+a4x2+a5x+a6(14)
式中 y——趋势项位移预测值;a1、a2、a3、a4、a5、a6——多项式系数;x——从1至N依次取值。
计算得到的拟合函数公式见式(15)。
y=-1.62×105x5+0.002234x4-0.109x3+2.219x2+1.718x+703.9 (15)
趋势项位移拟合结果见图9,且计算可得均方根误差(RMSE)为10.48 mm,虚拟优度R2为0.998 1,预测效果较好。
3.3 周期项位移预测
3.3.1 周期项检验
依据式(2)计算各时间段的自相关函数,计算结果见图10。自相关函数会在一个周期时出现明显的峰值,分析图10可知,峰值出现在每年的12月份,因此位移数据存在周期项,并且周期为12个月,与现实相符合。
3.3.2 周期项位移提取
从累积位移中剔除趋势项位移,即可得到周期项位移,见图11。将2007年1月至2012年12月的位移分解为趋势项与周期项,将2012年以前的数据作为训练集,2012年1—12月数据作为测试集。
3.3.3 影响因子关联度评价
一个灰色系统中,各个因素之间发展趋势的相似或相异程度,称为灰色关联度[16]。在演变过程中,如果两者的变化显示出较高的相似度,则认为两者具有关联。本文采用该方法计算单月降雨量、双月降雨量等影响因子与滑坡位移变化之间的关联度系数,从而判断该因子是否会对坡体位移演变产生影响,各个影响因子与滑坡位移关联度见表1。
当影响因子的关联度超过0.6,即可认为该因子滑坡位移的推进起到正向作用。由此可知,降雨量与库水位对位移变化量有相关性,因此本文将单月降雨量、双月降雨量、库水位高程、当月库水位平均值作为CNN-GRU预测模型中的输入数据,可以提高模型的预测精度。
3.3.4 周期项位移预测及结果对比分析
选用LSTM、GRU与CNN-LSTM 3种动态神经网络与CNN-GRU做对比,4种神经网络参数保持一致。
4种动态神经网络对周期项位移的预测结果见图12,基本上都能保持与周期项位移真实值保持一致。但是在阶跃式剧增部分GRU与LSTM预测效果并不好。4种网络预测效果排名依次为CNN-GRU网络模型、CNN-LSTM网络模型、GRU网络模型、LSTM网络模型。
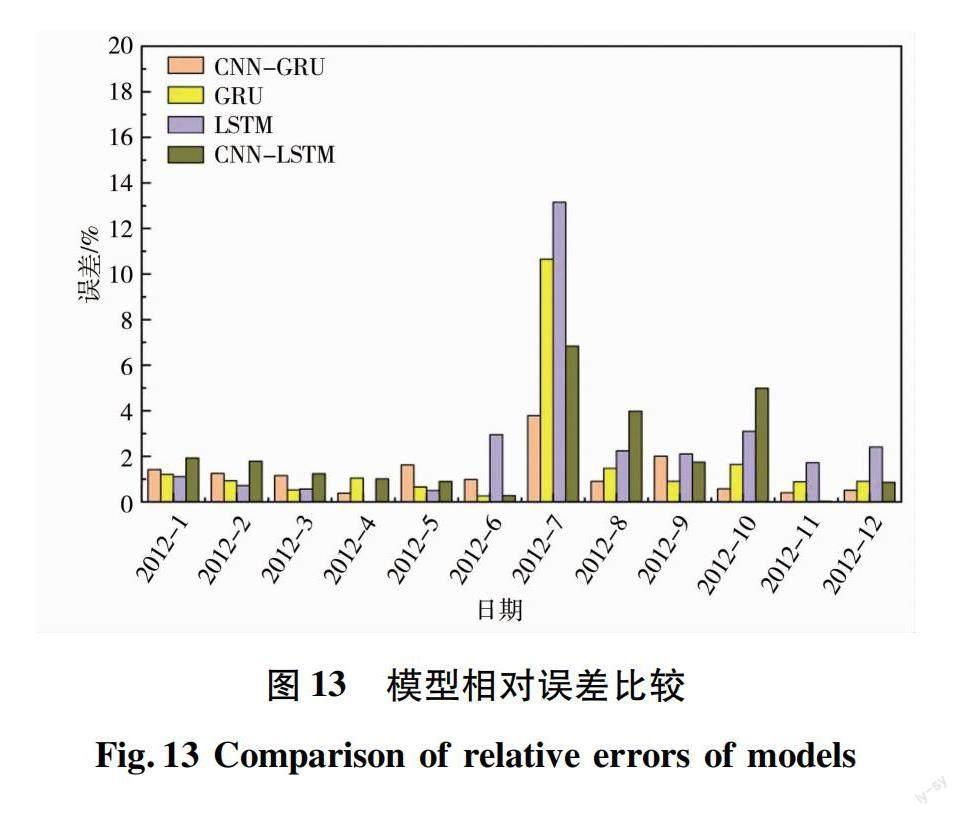
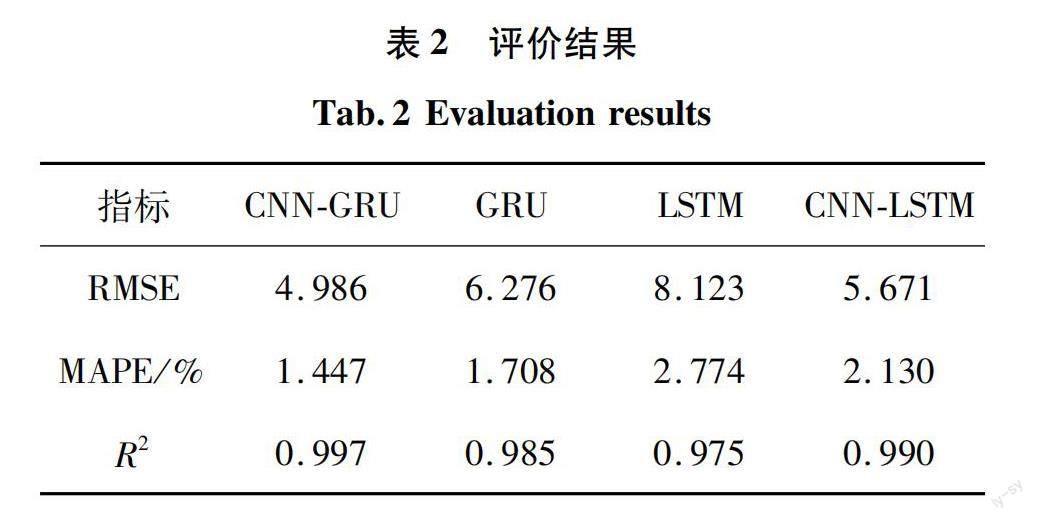
各模型相对误差误差见图13,评价指标结果见表2,具体分析如下。
a)在1—6月份未出现剧增数据前,4种预测模型都可以较好地跟随位移真实值的变化趋势。预测误差普遍较小,最大误差为LSTM网络模型6月份的2.953%。6—7月,位移出现剧烈增长,此时LSTM网络模型与GRU网络模型误差较大,分别为13.151%与10.656%。CNN-LSTM网络模型误差较小为6.84%,CNN-GRU网络模型精度最高,误差仅为3.789%。
b)7月之后位移进入递减阶段,分别于8、10月发生了2次较大幅度衰减,4种模型网络均可跟随变化,其中CNN-GRU的预测误差最低,分别为-0.903%与-0.578%。
c)CNN-GRU的RMSE为4.986,MAPE为1.447%,R2为0.997。指标结果均优于其他神经网络。
3.4 累计位移预测
将趋势项位移预测值与周期项位移预测值叠加,即可得到滑坡位移累计预测值。累计位移及误差见图14,预测值能够很好地跟随实际值,平均绝对误差百分比为0.525%,绝对误差百分比最高仅为0.742%,RMSE为9.614、MAPE为0.525%、R2为0.993。预测结果显示:CNN-GRU动态神经网络对于滑坡位移的预测精度比较高,能够很好地反映坡体的动态演化过程。
4 结论
本文将特征提取能力较强的CNN网络和变化趋势学习能力较强的GRU网络相结合,提出了基于时间序列和CNN-GRU动态神经网络的滑坡位移动态预测模型,并将此模型应于白水河滑坡监测点进行预测。
本文基于时间序列理论,使用小波分析与自相关函数分别检验滑坡位移的趋势特征与周期特征,保证了后续研究的合理性与可行性。引入指数平滑法,将累计位移分解为周期项与趋势项,相较于传统的移动平均法,能够保证得到的趋势项更加平滑,且更符合客观规律。对趋势项位移采用五次多项式函数进行拟合,擬合结果能够较好地跟随趋势项真实值演化过程。对周期项与各类影响因子采用灰色关联度分析,得到对周期项有影响的因子分别为单、双月降雨量、当月库水位高程、当月平均库水位。并采用CNN-GRU模型对周期项进行预测,将趋势项预测结果与周期项预测结果叠加得到累计位移预测值,累计位移预测值平均绝对误差百分比仅为0.525%,绝对误差百分比最高为0.742%,RMSE为9.614、R2为0.993。取得了较好的位移预测效果,可以为相似滑坡体提供预警服务。
参考文献:
[1]杨背背,殷坤龙,杜娟.基于时间序列与长短时记忆网络的滑坡位移动态预测模型[J].岩石力学与工程学报,2018,37(10):2334-2343.
[2]黄海峰,易武,易庆林,等.滑坡位移分解预测中的平滑先验分析方法[J].水文地质工程地质,2014,41(5):95-100.
[3]鄢好,陈骄锐,李绍红,等.基于时间序列和GRU的滑坡位移预测[J].人民长江,2021,52(1):102-107,133.
[4]宋丽伟.基于经验模态分解和LSTM模型的滑坡位移预测[J].人民长江,2020,51(5):144-148.
[5]张明岳,李丽敏,温宗周.RNN与LSTM方法用于滑坡位移动态预测的研究[J].人民珠江,2021,42(9):6-13.
[6]杨飞,郝晓莉,杨建,等.基于多车型CNN-GRU性能预测模型的轨道状态评价[J].西南交通大学学报,2023,58(2):322-331.
[7]彭伟,熊佳艺,江显群,等.基于神经网络的小型水库洪水预报研究[J].人民珠江,2023,44(3):1-8.
[8]郭子正,杨玉飞,何俊,等.考虑注意力机制的新型深度学习模型预测滑坡位移[J/OL].地球科学:1-21[2023-12-05].http://kns.cnki.net/kcms/detail/42.1874.P.20220823.0908.004.html.
[9]南骁聪,刘俊峰,张永选,等.基于多源时间序列的滑坡位移动态预测[J].人民珠江,2023,44(4):54-62.
[10]王连云,陶洪峰,徐琛,等.基于多层训练干扰的CNN轴承故障诊断[J].控制工程,2022,29(9):1652-1657.
[11]王锦涛,文晓涛,何易龙,等.基于CNN-GRU神经网络的测井曲线预测方法[J].石油物探,2022,61(2):276-285.
[12]WAN J,FU J F,TAN D M,et al.Solar Flare Forecast Model Based on Resampling and Fusion Method[J].Research in Astronomy and Astrophysics,2022,22(8):240-250.
[13]李麗敏,张明岳,温宗周,等.基于奇异谱分析法和长短时记忆网络组合模型的滑坡位移预测[J].信息与控制,2021,50(4):459-469,482.
[14]陈锐,范小光,吴益平.基于数据挖掘技术的白水河滑坡多场信息关联准则分析[J].中国地质灾害与防治学报,2021,32(6):1-8.
[15]乔素云,马云彪,尹思杰,等.基于岩土参数变异特性的三峡库区白水河滑坡失稳概率分析[J].中国地质灾害与防治学报,2018,29(5):38-43,51.
[16]程立文,黄生志,李沛,等.耦合二次因子筛选和深度学习的径流预报研究[J].人民珠江,2023,44(6):41-52,69.
(责任编辑:李泽华)
