“问探讲”课堂模式下跨学科问题链的设计研究

吴维 陈俊睦 蔡佳

《義务教育课程方案和课程标准（2022年版）》提倡“加强课程综合，注重关联”，规定了各门课程都应该设置不少于10%课时的跨学科主题学习，这就要求学校开展跨学科教学，培养学生的综合素养。学始于“问”，为更好地践行新课标要求，笔者根据学校“问探讲”教学模式，围绕跨学科问题链的设计展开教学研究。

一、设计跨学科“大问题”

“问探讲”跨学科问题链设计，以“跨学科主题学习”理念为指导，以“问探讲”教学模式中的“问”为根本，通过设问将不同学科领域的知识融合起来，形成互相关联的问题链，帮助学生更好地理解和掌握知识。在设计跨学科问题链时，首先需要确定主题，根据主题选取一个问题作为起点，这个问题一般是该学科本节课统领性的“大问题”。设计“大问题”时可以考虑以下几个步骤：①分析本主题关联学科的核心素养，具体到知识、技能、思想方法、情感态度和价值观等；②考虑学生学情与兴趣，了解学生的需求和动机，设计贴近学生生活和兴趣的大问题，提高学生参与度和投入度；③确定教学目标，初步确定“大问题”；④思考该“大问题”的开放性、创新性，最终确定“大问题”。大问题的设计要考虑不同学习经验、能力的学生，在“探”和“讲”的过程中给予学生多元思考空间和创造性表达的机会。需要注意的是，“大问题”是本节课的核心内容，一旦确定下来，一般不作调整。

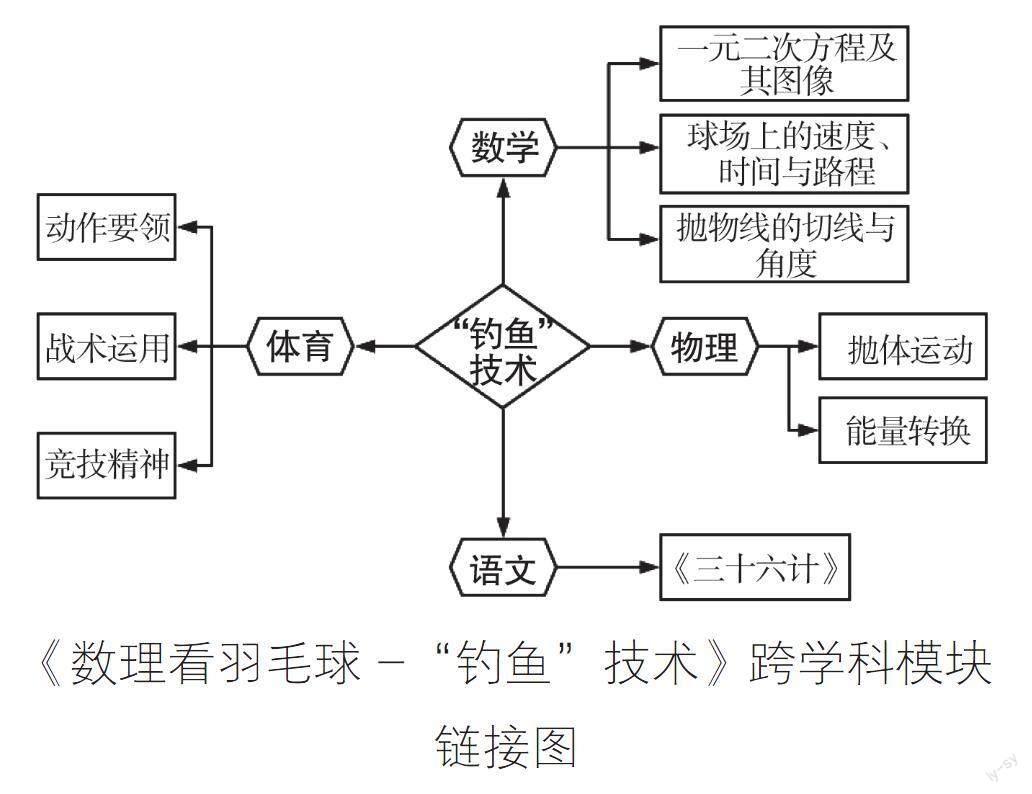
案例：数理看羽毛球-“钓鱼”技术。

“钓鱼”技术指在羽毛球比赛中处理网前球时，把球的弧线放得很高，羽毛球的飞行路线近似开口向下的抛物线，将抛物线的最高点控制在自己的场地内，当球过网时，近乎贴网垂直下落，造成对方网前回球难度大，最后结合进攻得分。可以看到，“钓鱼”技术与一元二次方程有着密不可分的联系。“一元二次方程”是北师大版数学九年级上册第二章的内容，学生在前面的课程学习中已经经历了“问题情境－建立方程模型－解决问题”数学化的过程，理解了学习一元二次方程的意义，能够通过寻找其中的数量关系来解决简单的实际问题。但这些问题通常是已经高度数学化的生活模型，学生虽然经历了这些问题的解决过程，但能力尚不足以充分将生活实际情景抽象为学科模型，以及跨学科调用、整合知识解决问题，即学生数学抽象、数学建模的数学核心素养培养力度仍不够。因此，我选择学生常见、喜爱的羽毛球“钓鱼”技术为切入点开展跨学科教学实践，使学生认识一元二次方程建模在体育运动中的具体应用，自然地感受到跨学科学习的意义和妙用，培养学生综合学习的兴趣。

根据学科素养和学情导向，我将本节课教学目标定为：①理解羽毛球“钓鱼”技术的技术要点，熟悉“钓鱼”技术的战术组合；②经历“钓鱼”技术抽象成数学、物理模型的过程，会用数学、物理眼光观察“钓鱼”技术；③结合模型、类比的思想方法，能用数学二次方程、物理斜抛的知识分析、解释“钓鱼”技术；④激发学生运用数理知识探索体育运动的兴趣，提升学生的综合运用能力。教学重点是经历“钓鱼”技术抽象成数学、物理模型的过程，会用数学、物理眼光观察“钓鱼”技术。教学难点是能用数学、物理的知识分析、解释“钓鱼”技术。

根据以上分析，本节课以概念型大问题“什么是羽毛球‘钓鱼技术？”引入，抛出该大问题时播放经信息技术处理后的视频（将羽毛球的飞行路线抽象出数学轨迹），帮助学生在认识“钓鱼”技术的同时，建立数学表征。

二、建立跨学科学习链接

“大问题”是“源”，“子问题”是水，我们要根据“大问题”设置“子问题”。在建立跨学科学习链接时，不同学科领域的教师可以共同参与问题链的设计和实施，相互交流并贡献各自的专业知识。这里可根据主题或者“大问题”链接多个相关学科的知识模块，包括物理、数学、科学、工程、社会、人文等，并经各个模块衍生出相关子问题。这些子问题与大问题息息相关，贴近实际应用场景，对达成本节课教学目标有促进作用，但可以因课程的需要、学生实际水平灵活调整。需要注意的是，假如延伸的跨学科子问题对问题的解决贡献不大，为避免造成课堂主次不分的情况，则不应占用课堂太多时间。

三、深加工问题链层级

在明确主题和跨学科模块后，需要按照一定的逻辑，确定问题链的结构和层次，最终形成问题链。问题链的问题来源既可以是“大问题”所拆解的小问题，也可以是跨学科模块衍生的小问题。每个小问题都是学科知识的生长点，它们之间既可以是递进关系，层层深入问题的“探讲”，加深学科的综合理解；也可以是并列关系，为其他生长点提供养分，相互促进理解。在后续的“探”和“讲”中，通过逐个解决这些小问题，逐步解决跨学科探究主题的问题。在问题链的设计或实施过程中，还需要及时反思和调整问题链的设计，如果发现某个小问题无法有效解决或者拖慢主线的进度，则需要及时调整问题链的设计思路，将该小问题重新分解为更小的问题或者替换，以便更好地解决它，确保问题链的有效性和可持续性。

上述案例中，本节课以“是什么—怎么做—为什么这么做”为逻辑主线编排问题链，在了解什么是“钓鱼”技术之后，提出“‘钓鱼有哪些技术要领？”，即“怎么做”。在“为什么这么做”这一步，综合链接数学、物理相关知识模块，设计小问题进行深度追问。首先提出“为什么要控制羽毛球的最高点在自己的场地内？”这里抽象出羽毛球飞行路线图（抛物线图像），从图像可以看到，同一击球点同一最高高度，假如最高点在己方场地内，则羽毛球在对方场内下坠时会更贴网。学生根据现实经验，容易得到“对手回球难度更大”的结论。自然而然地引出下一个追问：“为什么最高点在己方场地就会增加对手回球的难度？”引导学生从“速度、时间与路程”这一数学知识角度上理解：羽毛球从同一起点做斜抛运动，到达相同高度经过的时间相同，假如把最高点控制在偏向自己的场地内，则相同时间内对方球员要移动去接球的距离更长，接球难度更大。实际上，“抛体运动”是高中物理才学的内容，这里从数学角度进行简单的渗透，也为后面的学习作了初步铺垫。

最后从战术组合上，进一步追问：“为什么要控制‘钓鱼球一过网即贴网近乎垂直下落？”引导学生进一步分析图像，从切线及其与地面夹角可以发现：控制羽毛球过网即坠，对方回球的路线受限，球越贴网，自己就能站在更近的地方扣杀球，威力越大，对手越难接。

四、系统化审视和调整问题链

在完成所有问题设计之后，还需要依据上述原则对整个问题链的设计进行总结和反思，系统审视问题设计是否符合学科背景、激发学生兴趣等；问题的难度和复杂程度是否适合学生的认知水平；问题链的设计是否枝强干弱、本末倒置等。假如某些问题不合适，则需返回该节点重新设计。

本文的案例中，课程内容的学习围绕学生感兴趣的羽毛球运动背景展开，以数学知识“一元二次方程”为本，结合数学、物理、体育、信息技术等学科，改变了以往抽象、枯燥的孤立学科知识教学，学科知识联系紧密，触类旁通，跨学科内容融合成了一个合理协调、相互促进、富有创造性和发展性的资源整体。在整个教学设计中，学生的主体性和个性化发展得到充分重视，这样的教学方式有利于学生创新精神和问题解决能力的培养。问题链的设计上，从主题“一元二次方程的应用”开始，围绕一元二次函数图像，拋出大问题“什么是羽毛球‘钓鱼技术”，直观理解“钓鱼”技术，知道其概念和技术特点。接下来递进式地将大问题分为几个小问题进行“探”和“讲”，从“为什么要控制羽毛球的最高点在自己的场地内”，继续追问“为什么会增加对手回球的难度”，再到“为什么要控制羽毛球过网即坠”，将体育、物理、信息、美术、数学等不同学科领域的知识融合起来，形成一个基于“一元二次方程”的跨学科问题链，帮助学生从不同角度全面理解一元二次方程图像及其应用，深刻地认识体育运动所蕴含的科学知识。最后，将主题升华到“体育竞技精神和学科学习”，希望学生既能用学科知识认识世界，又能将“迎难而上、拼搏进取”的体育竞技精神在学科学习中发扬光大。问题链整体呈先总后分、逐级递进的思维梯度，帮助学生养成综合、有序、深入思考的思维习惯，最后的总结跨越知识维度，升华精神境界。

五、结语

跨学科问题链的设计是一项复杂的任务。综上所述，通过“确定主题—选取大问题作为起点—建立跨学科学习链接—深加工问题链层级—系统化审视和调整问题链”等一系列流程，教师可以有条理地进行跨学科教学设计，有助于学生更好地全面理解与掌握跨学科知识，提高学生的综合素养。

注：本文系2021年度广东省中小学教师教育科研能力提升计划项目课题“基于学科课程综合的问探讲教学模式研究“（课题编号：2021YQJK081）、佛山市南海区教育科学“十四五”规划2021年度立项课题“‘问探讲课堂模式下跨学科融合教学策略研究”（课题编号：NHZD2021010）的研究成果之一。

责任编辑 罗 峰