Exploring reservoir computing:Implementation via double stochastic nanowire networks

Jian-Feng Tang(唐健峰), Lei Xia(夏磊), Guang-Li Li(李广隶), Jun Fu(付军),Shukai Duan(段书凯),3,4, and Lidan Wang(王丽丹),2,3,5,6,†

1College of Artificial Intelligence,Southwest University,Chongqing 400715,China

2Brain-inspired Computing&Intelligent Control of Chongqing Key Laboratory,Chongqing 400715,China

3National&Local Joint Engineering Laboratory of Intelligent Transmission and Control Technology,Chongqing 400715,China

4Chongqing Brain Science Collaborative Innovation Center,Chongqing 400715,China

5Key Laboratory of Luminescence Analysis and Molecular Sensing,Ministry of Education,Southwest University,Chongqing 400715,China

6State Key Laboratory of Intelligent Vehicle Safety Technology,Chongqing 400715,China

Keywords: double-layer stochastic(DS)nanowire network architecture,neuromorphic computation,nanowire network,reservoir computing,time series prediction

1.Introduction

In recent years,neuromorphic computing has emerged as a promising technology in the post-Moore’s law era, attracting significant attention due to its high degree of connectivity,parallelism and relatively low power consumption.[1]The primary objective of neuromorphic computing is to overcome the main limitation of traditional von Neumann computing architectures;specifically,the data transfer bottleneck known as the von Neumann bottleneck.The progress of neuromorphic computing and engineering depends on the development of new hardware technologies and architectures that mimic the functions of biological neuron circuits.Memristor devices,which can store and process data in the same physical location, play a vital role in bio-inspired and neuromorphic computing.Devices with memristor characteristics can imitate biological synaptic functions, emulate efficient human brain functions and provide hardware support for realizing trusted architectures.Numerous studies have reported the use of devices with memristor properties to achieve artificial synapses,including resistive random-access memory with drifting[2]and diffusive[3]memristors.The paper[4]reports on the implementation of a two-dimensional memristor-based sensor using tin sulfide (SnS) for language learning.It demonstrated an accuracy of 91% in classifying short sentences, showcasing a low-cost,real-time solution suitable for time and sequence signal processing in edge machine learning applications.In the study,[5]a memristor-based reservoir computing system is presented,utilizing the internal short-term ion dynamics of memristive devices and the concept of virtual nodes.It successfully demonstrates time series analysis and prediction tasks.In the research,[6]ultralow-power, high-precision image processing and dynamic video analysis are achieved by utilizing a nonlinear,spatiotemporal correlated photocurrent to construct an internal reservoir computing system within a sensor.Additionally,many studies have utilized memristor devices as modules to simulate synaptic functions[7,8]and research has shown that forming memristor devices in large-scale crossbar arrays for the realization of artificial neural networks and neuromorphic computing is one of the most promising approaches at present.[8]

However, the hardware architecture of regular arrays of amnestic devices is quite different from the intrinsic structural complexity of the human brain and cannot simulate the topology and emergent behavior of biological neural networks.Consequently, researchers have focused on another type of hardware neural network based on memristor synaptic devices,with nanowire networks emerging as a unique representative class.Nanowires network consists of randomly arranged wires,no more than 10µm long and no thicker than 500 nm,in a two-dimensional plane.Where the wires overlap in the network,they form an electrochemical node resembling a synapse between neurons.Hochstetteret al.has proposed a neuro morphodynamic model for nanowire networks that adapt in a brain-like manner.[9]The electrical signals passing through this network automatically find the best path to transmit information and remember previous paths through the system.[10]Professor Tomonobu Nakayama has extensively researched nanowire networks,including their dynamic behavior and network topology.He has demonstrated that nanowire networks respond adaptively to time-varying stimuli, exhibit diverse dynamics that can be tuned from ordered to chaotic and illustrated that ‘avalanche criticality’ and ‘chaotic edge criticality’ in nanowire networks can optimize increasingly complex learning tasks.[11]The nanowire network employs a topdown nanofabrication approach, allowing for higher interconnectivity of amnestic crosspoint junctions.In terms of structure and functional relationships, the nanowire network has strong similarities to real(bio)neural networks formed by bottom-up self-assembly.Meanwhile, self-organizing random nanowire networks composed of nano-objects have recently been demonstrated for the physical implementation of neuromorphic information processing.[9,10,12,13]This random self-organized structure is more consistent with the biologically based neuromorphic architecture than the regular memristor array.Fuet al.[14,15]demonstrated the ability of a selforganized random nanowire network to implement reservoir computation.

In reservoir computing models, the internal reservoir units are determined by a random sparse matrix of connections.[16]The reservoir network maps the input to a high-dimensional dynamic space, with the values of multiple reservoir nodes determining the mapping result.The mapped data is then fed into the readout layer for classification or prediction.Only the readout layer weights need to be trained,significantly reducing computational effort and improving the network’s computational efficiency.A self-organizing random nanonetwork is a highly interconnected network of random nanowires that intersect to form nodes with amnestic properties.The network’s overall dynamic behavior arises from the collective behavior of multiple nano nodes.Self-organized stochastic nanonetworks have also been shown to exhibit rich neuromorphic dynamics,[17-20]such as short- and long-term plasticity, heterosynaptic plasticity and chaotic edge properties.The structural and functional similarities between selforganized stochastic nanonetworks and reservoir networks justify using self-organized stochastic nanonetworks as an internal implementation of reservoir computing.

Hochstetteret al.[11]and Zhuet al.[9]introduced a random nanowire network model, suggesting that the network’s size and complexity are associated with the average variance and length of the nanowires.The model employs a threshold equation to represent the dynamics of each memristor edge and assumes uniform behavior across all nanowire junctions in the network.Ricciardiet al.[21]presented a grid graphical modelling method for memristor nanowire networks,where a physics-based accretion-inhibition rate balance equation governs each edge’s dynamic behavior.However,due to the randomness of mechanical contact, the resistive state and memristor effect of nanowire nodes are randomly distributed, rendering the model incapable of accurately representing the network’s dynamic behavior.

In this paper, we design a nanowire network model that better aligns with the hardware characteristics of the process.By combining the features of nanowire networks,we propose converting data into voltage pulses of varying amplitudes as input to the network,thereby reducing information processing time and enhancing computational efficiency.We develop a double-layer stochastic (DS) reservoir network based on the nanowire network,utilizing the random distribution of voltage states at the nodes and the rich dynamic behavior of the web to construct a reservoir network.This design also incorporates the nanowire network’s ability to process multiple input signals in a spatiotemporal manner.We test the DS reservoir network’s performance on real-time series data,and our experiments demonstrate the superior accuracy and stability of the nanowire network-based reservoir system compared to traditional reservoir networks.In terms of energy consumption,a study conducted by Milanoet al.in 2022 found that the total energy consumption of a single input is 750 µJ, which is higher than the energy consumption of a single memory resistor device in traditional top-down reservoir computing systems.However, by utilizing shorter pulse widths and adjusting material properties,it is possible to further reduce energy consumption, thus providing potential for nanowire networks in future complementary metal-oxide-semiconductor integration.[13]

2.Network modeling and analysis

2.1.Dynamic modeling of memristive resistance for random network graphs

Zegaracet al.[22]established a link between graph theory and the dynamics of memristive circuits.Milanoet al.[23]employed a graph-theoretic approach to investigate the functionality and connectivity of random nanowire networks,introducing the concept of memristive graphs.These graphs represent random nanowire networks as weighted directed graphs,with nodes symbolizing nanowire junctions and connected edges denoting the relationships between them.Montanoet al.[21]utilized a grid model to simulate nanowire network connections,where nodes are regularly connected,simplifying calculations and network complexity to some extent.This model offers a general platform for exploring non-traditional computational paradigms in nanowire networks.

However, randomly connected nanowire networks more closely resemble the inter-synaptic connections of brain neurons and the connections within reservoir computing.Therefore,in this paper,we opt for random nanowire network simulation to implement reservoir computing and adopt a graph theory approach to simulate the dynamic behavior of the random nanowire network.Milanoet al.[17]observed that when a random nanowire network is dynamically stimulated by an external voltage,a process occurs on two outer-wrapped insulating polyvinylpyrrolidone silver nanowires,forming a silver conductive bridge.The formation and rupture of this bridge result in a resistance switch.

The network dynamics rely on the collective behavior of numerous nanowire nodes within the network and can be modelled based on the memristor behavior of a single nanowire node.To simulate the model of short-term plasticity,a single nanowire node is developed,and the network memristor edge dynamics are modelled using a voltage-controlled potentialinhabitance balance equation.The voltage difference between various nanowire nodes in the network and the relationship between the currents flowing between the nodes under this voltage difference is represented by

whereGlowandGhighdenote the minimum and maximum conductance of the memristor edge,respectively;whileg(t)represents the normalized conductance of the memristor edge,normalized between 0 and 1.The current relationship ofI(t)follows Ohm’s first law.The memristor edge conductance variation is expressed by a voltage-controlled potential-inhibit rate balance equation

In this equation,ωaandωbare functions of the input voltage controlled by the input voltage,representing the inhibition and enhancement coefficients that control the conductance change,respectively,

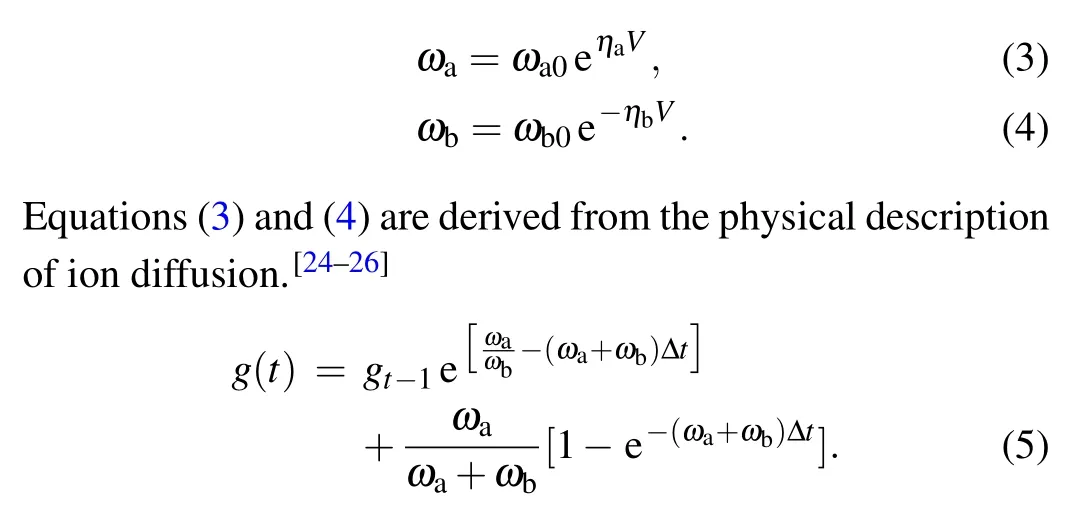
Equation (5) can be solved recursively.Following Mirandaet al.’s approach[27]for handling continuous functions in a discrete-time domain, our model employs the same concept,allowing the model to represent the network’s response to arbitrary input voltages.It is important to note that the initial conductance of the memristor edge is uniform and identical to the initial case conductance.Equation(5)is divided into two parts: the first part signifies the network’s historical memory state,while the second part represents the network’s constantly changing process under external input voltage stimulation.

2.1.1.Analysis of the dynamic behavior of random nanowire networks

In this study, we explore the changes in conductance within a nanowire network when exposed to constant external voltage stimulation.The network features two external terminals: an input terminal for voltage and an output terminal where voltage remains at 0.As external voltage is applied to the input terminal, a spontaneous connectivity path forms between the input and output terminals, resulting in conductance changes within the network.Figure 1(a) illustrates the time-dependent trajectory of effective conductance changes for a realistic Ag nanowire network with a two-terminal configuration under constant voltage pulse stimulation.[23]Meanwhile, Fig.1(b) presents the trajectory for a previously designed nanowire model subjected to the same stimulation.When compared to earlier research,[23]the conductance change curve in Fig.1(b)more closely resembles the actual double-ended configuration of the nanowire network under identical experimental conditions.

The nanowire network’s effective conductance is enhanced by constant voltage pulse stimulation,and without external voltage stimulation,the network conductance gradually decreases and spontaneously relaxes.Conductance changes at each edge of the network are governed by the enhancementinhibition rate balance equation.A detailed comparison of Figs.1(a)and 1(b)indicates that the experimental results align well with the model results during both the enhancement and relaxation phases.This observation confirms the proposed model’s ability to accurately simulate the behavior of real nanowire network dynamics in response to external stimulation.

Furthermore,Fig.2 illustrates the dynamic emergent behavior of the network under external constant pulse stimulation.The nanowire network’s conductance continuously increases in response to external voltage stimulation, progressively forming a conduction path between the voltage input and output terminals.As the external voltage stimulation persists,conduction paths are continuously redistributed,leading to the formation of an increasing number of paths within the network.This redistribution of conduction paths highlights the self-organizing characteristics of the nanowire network.

Fig.1.(a) Plot showing the trajectory of the effective conductance of the Ag nanowire network with time in the experiment under constant voltage pulse stimulation,and(b)plot showing the trajectory of the effective conductance of the network simulated according to the model.

In the absence of voltage stimulation,the network memristor edge conductance gradually decreases,causing the conduction paths to dissolve and the network conductance to revert to its initial state.The interplay between the enhancement of network conductance under external voltage stimulation and the spontaneous relaxation of the network conductance state enables the network to accumulate information,providing it with the capacity to process complex and datarich inputs.In a study,[20]the network achieved continuous and adaptive reconfiguration by enhancing the main current pathways and detecting the presence of multiple conduction channels, demonstrating remarkable fault-tolerant capabilities.These silver nanowires self-assembled into a neuralmorphic system composed of polymer-coated silver nanowires with resistive switching junctions.

Further research[11]demonstrated that the neural-morphic nanowire network exhibited adaptive and collective responses to electrical stimulation, achieved through a phase transition of threshold voltage and conductivity.Intersection points in the network formed avalanche collective switching,consistent with avalanche phenomena at critical voltage.At high voltages, both large-scale and small-scale avalanches coexisted.Under alternating polarity stimulation,the network could regulate between ordered and chaotic states.These findings suggest that the neural-morphic nanowire network can be tuned to exhibit collective dynamic mechanisms similar to the brain,optimizing information processing.This further underscores the powerful capabilities of nanowire networks in information processing.Moreover,this model simulates the collective dynamic behavior of nanowire networks with reduced time costs and improved computational efficiency, allowing for the simulation of networks on personal computers to study the selforganized behavior of network conductivity change pathways.It is worth noting that the conduction pathways formed after the simulation are consistent with the experimental evidence reported by Liet al.[28]and the computational model reported by Manninget al.[29]

In this article, we directly observe and analyze the network voltage distribution through the model.During the experiment,we apply a constant pulse voltage stimulation to the network voltage input terminal while maintaining the output terminal voltage at zero.As shown in Fig.3(a), the voltage distribution of different nodes in the network under external voltage stimulation is plotted.Through this model, we can directly observe and analyze the voltage changes of network nodes at each moment.From Fig.3(a), we can find that under constant pulse voltage stimulation,the voltage changes of different nodes in the network exhibit variability.This variability is due to the spontaneous formation and dissolution of conduction pathways caused by the memristive edge conductance characteristics of the network, resulting in different nodes in the network having different voltage changes in the time dimension.This endows the network with rich emergent dynamic behaviors.

To further demonstrate the spontaneous behavior characteristics of the network conduction pathways, we apply constant pulse voltage stimulation to 10 different pairs of terminals in the network (these 10 pairs of terminals have the same voltage input terminals and different output terminals)and record the voltage changes of the same nanowire node.Figure 3(b) shows the voltage differences and emerging dynamic behaviors of some network nodes under different terminals with constant pulse voltage stimulation.

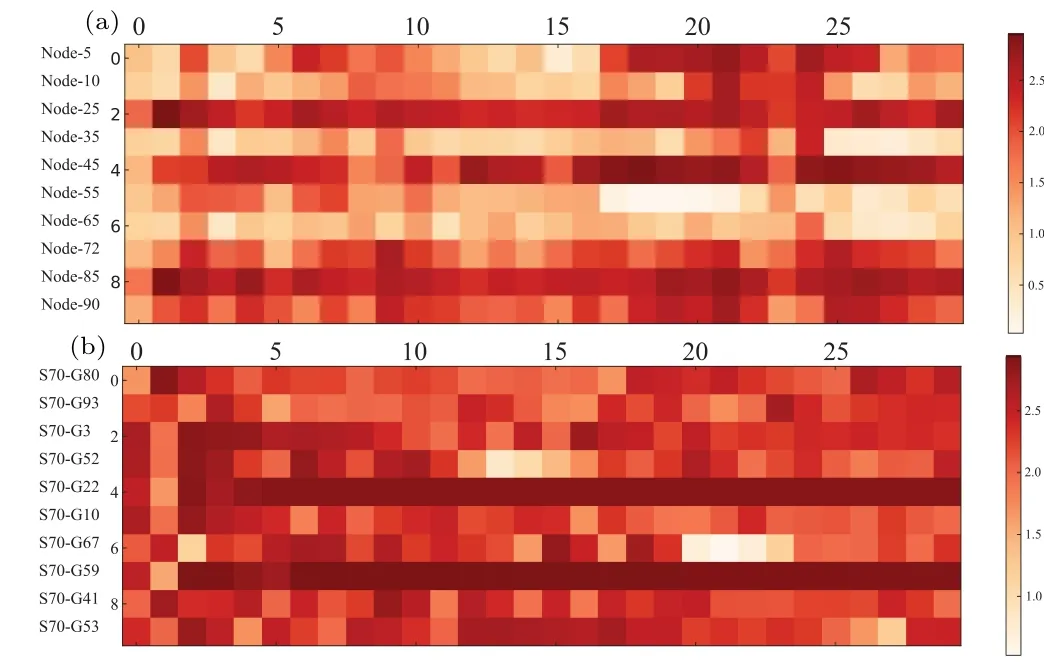
Fig.3.(a)Simulation of the different nodes’voltage changes V in the network under a constant external voltage stimulus of 3 V.The color shades in the figure indicate the node voltage intensity.(b)Simulation of the same node voltage changes V in the network under a constant external voltage stimulus of 3 V,but with different positions of the network output terminal while keeping the voltage input terminal fixed.The color shades also represent the node voltage intensity.

The experimental results show that when constant pulse voltage stimulation is applied to different terminals, different conduction pathways will spontaneously form between network nodes,leading to different voltage changes for the same node.This phenomenon indirectly reflects the relationship between the emergent dynamic behavior inside the network and the position of external electrical stimulation.The experiment proves that, under external stimulation, the network interior will generate complex emergent dynamic behaviors.Through this model, we can analyze the network node voltage, network conductance changes,and the formation and dissolution of network conduction pathways in the time domain.Therefore,this model can serve as an effective tool for studying and learning the dynamic behavior of nanowire networks.

3.The DS nanowire network

3.1.Deep echo state network

Reservoir computing models have gained popularity in various applications, including image classification[30]and time series prediction.[31,32]The echo state network(ESN),[33]a widely used reservoir computing model, differs in function and structure from artificial neural networks and recurrent neural networks.ESNs employ a random sparse matrix to determine their internal connections.Data is mapped to a highdimensional dynamic space by the reservoir network and then input to the readout layer for classification or prediction.In ESNs,only the readout layer weights require training,significantly reducing computational effort and enhancing the network’s efficiency.The random cyclic connections in the ESN’s reservoir layer are well-suited to time series prediction and have achieved notable results across various fields.[34-37]To augment the information processing capabilities of ESNs,Pedrelliet al.[38]introduced the deep ESN concept, which emphasizes the hierarchical nature of the reservoir.Deep ESNs offer considerable advantages over single-layer ESNs,improving the reservoir state’s richness and the network’s memory capacity.The deep ESN structure is depicted in Fig.4.In this network, the first layer is internally connected and functions similarly to the reservoir layer in a single-layer ESN.As the network deepens, the previous layer’s state is input to the subsequent layer.

Fig.4.Deep echo state network structure.

The first layer state transfer function is defined as follows:

When the number of layers is greater than 1,the state transfer function is defined as follows:

where each network layer has the same reservoir unitN, the subscript[m],denotes themth layer of the network,timetandt-1 denote the current momenttand the last moment at layerm.Winis the input weight matrix,W[m]is the interlayer connection weight matrix from layerm-1 to layerm, ˆW[m]is the recursive weight matrix of layerm,a[m]is the leakage parameter of layerl.The tanh is equivalent to the activation function in a convolutional neural network providing nonlinear states.

Fig.5.A conceptual schematic of the random nanowire network-based reservoir computing for time series prediction.The steps involve (1)data preprocessing, (2) data encoding and transmission in the random nanowire network, and (3) readout layer processing and prediction of the output sequence from the reservoir.

Pedrelliet al.[38]introduced a deep neural network model that efficiently handles complex time series data by exploiting hierarchical temporal scale differences.Based on the deep ESN model, we propose double-layer stochastic (DS)nanowire networks to overcome the limitations of single-layer nanowire networks in generating rich nonlinear behaviors.This approach is a key step towards developing deep reservoir computing based on nanowire networks.The DS architecture enhances the predictive capability of reservoir computing based on nanowire networks for time series.As shown in Fig.5,reservoir computing is implemented using a singlelayer nanowire network withNnodes.We suggest converting the data into pulse voltages with different amplitudes and then inputting them to the voltage input terminal node.According to the principle of reservoir computing, the input voltage data is mapped to various node voltages within the nanowire network, and time series information is processed by analyzing the voltage changes of different nodes in the time domain.First, we normalize the input time series data between 0 and 1 and input it to the nanowire network.Then, we convert the data into pulse voltages with different amplitudes and introduce them to the voltage input terminal.As the input voltage fluctuates,the node voltages within the nanowire network change continuously,and the voltage change of each node depends on its historical input voltage.When an external voltage stimulus is applied to the network, the voltage distribution of different nodes in the nanowire network changes.By analyzing the voltage changes of different nodes over time, we can predict data trends.In the whole process, we read a part of the node voltage state values at each moment for subsequent data analysis and processing.Finally,we input all the obtained node voltage state values to the network readout layer for further processing and interpretation.

The role of the readout layer in the DS nanowire network is to convert the internal state of the network into usable outputs,enabling the network to make predictions,perform classifications, or other tasks.The readout layer is the only part of the network that undergoes training and is typically solved using the ridge regression method.In the DS nanowire network we designed,the global reservoir stateXin the network is composed of the states from different network layers.As shown in Fig.6(a), the readout layer is directly connected to nodes in two different nanowire network layers using a fully connected approach.This allows for direct collection of the state of each nanowire network node for training purposes,and the internal voltage state vectors of different network layers are horizontally stacked to generate a global state vector.Regarding the training algorithm, the output layer in the DS nanowire network is trained using the standard reservoir computing paradigm.[39]Specifically, we use the ridge regression algorithm to obtain the output weight matrixWoutas follows:

Here,Ytargetrepresents the target for prediction,Xrepresents the high-dimensional vector generated by the nanowire network layer,Irepresents the identity matrix,γis the regularization coefficient andIrepresents the identity matrix.The symbols “T” and “-1” denote matrix transpose and inverse operations,respectively.

To summarize, in the DS nanowire network, the global reservoir stateXis composed of the states from different network layers.The output layer is trained using the ridge regression algorithm based on the standard reservoir computing paradigm to obtain the output weight matrixWout.During training,the output weight matrix is computed by multiplying and inverting the product of the target for predictionYtarget,the high-dimensional vector generated by the training layerX,the regularization coefficientγ, and the identity matrixI.After training is completed,Woutcan be directly used for prediction.

We propose a DS nanowire network model, which consists of two nanowire network layers with unique network connectivity and random node distribution, as depicted in Fig.6.This design overcomes the limitations of singlelayer nanowire networks, such as limited node number, reduced network complexity and unsatisfactory predictive performance.The DS-nanowire network is primarily manifested in two aspects: first, the randomness in the connections between nanowire nodes within each layer of the multi-layer nanowire network, and second, the variability in the connections between different layers of the nanowire network.Additionally, the inter-layer connections are established through random one-to-one connections, ensuring both accurate data transmission and enhanced nonlinearity and expressive power of the network.By increasing the nanowire nodes and generating more diversified node states,the model is more suitable for time series prediction, providing an implementation strategy for reservoir computing in multi-layer nanowire networks.

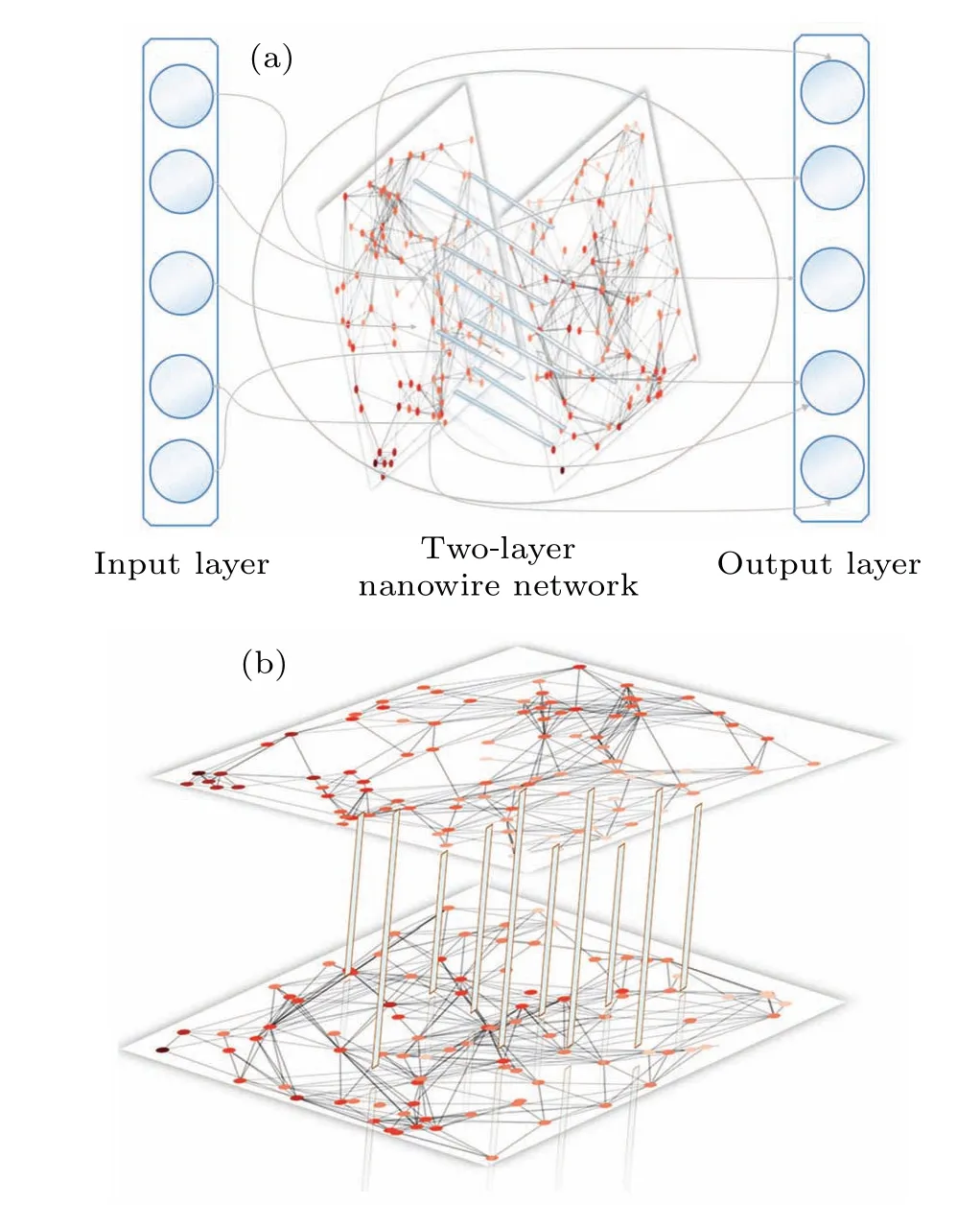
Fig.6.(a) Conceptual schematic of the DS nanowire network-based reservoir computing for time series prediction.(b) Schematic diagram of the nanowire reservoir structure of the DS nanowire network model.The reservoir structure consists of a randomly generated duallayer nanowire network, and the network layers are connected using a one-to-one node mapping method,i.e.,each node in the upper network corresponds to a node in the lower network.

The proposed DS nanowire network model has a novel reservoir network structure with single-input-multi-output and multi-input-multi-output capabilities, which are formed by processing the node voltage state values of both network layers in the readout layer.In the DS nanowire network, the input data is mapped to intermediate node voltage state values through the first nanowire network layer at each moment, for a certain number of nodes (15 nodes are used in the experiment).Taking advantage of the ability of nanowire networks to process multiple input signals in spatiotemporal modes,the node voltage state vector serves as the input for the subsequent network layer.The lower layer network input terminal accepts the intermediate node voltage state vector as the network input, processes the intermediate node state values and outputs node voltage state values.The DS architecture is adopted for practical reasons, as it is challenging to fabricate two identical nanowire networks in the production process.The architecture is compatible with the nanowire network layer and ensures satisfactory performance.We evaluate the predictive capability of the DS nanowire network using three real-world datasets.By combining nanowire networks with reservoir computing and using node voltages as intermediate voltage states,the nanowire network structure is consistent with the reservoir layer structure of reservoir computing,paving the way for hardware implementation of deep reservoir computing.

4.Experiment

4.1.Dataset introduction

In this section, we assess the prediction performance of single-layer ESN, layered ESN, single-layer nanowire network,and our proposed DS-nanowire networks on three realworld time series datasets: the sunspot time series dataset,the Birmingham parking dataset and the bike-sharing dataset.

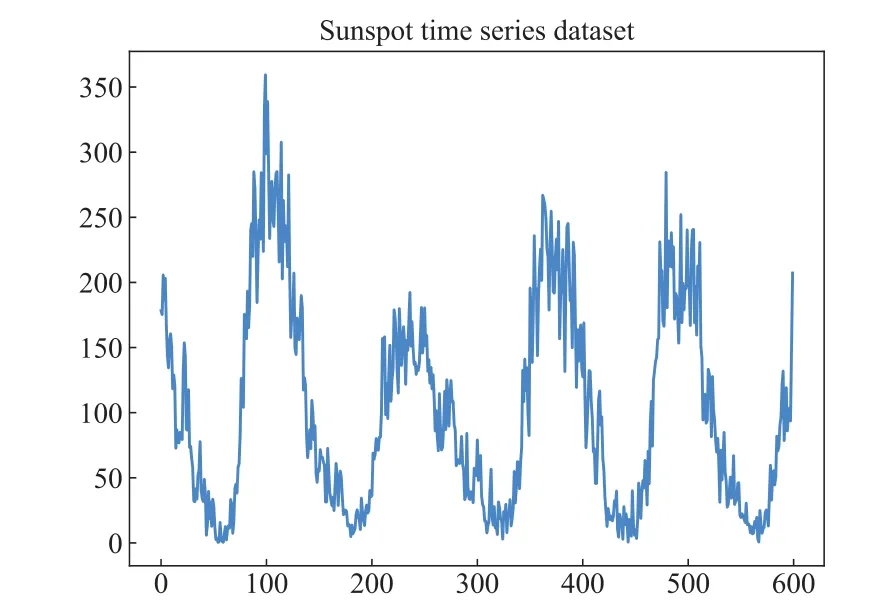
Fig.7.Sunspot time series dataset(first 1000 points).The x-axis coordinates represent the collection sampling points and the y-axis coordinates represent the sunspot data.

Sunspot time-series predictions Sunspots reflect the dynamics of the strong magnetic field surrounding the Sun,and their numbers correlate with solar activity.The unpredictability and complexity of solar activity result in strong nonlinearities in sunspot sequences, making them suitable for testing network models’ ability to solve real-world time-series prediction problems.We use a 13-month open-source monthly unsmoothed sunspot series provided by the World Data Centre SILSO,[40]collected from January 1749 to March 2021,containing 3267 sunspot sampling points.In our experiment,the first 2200 sequence sampling points serve as the network training set,2200-2400 sequence sampling points as the validation set, and 2400-3000 sequence sampling points as the test set,performing one-step ahead direct prediction.The sunspot time series data is shown in Fig.7.

Birmingham parking dataset Sourced from the UCI Machine Learning Repository,[41]this dataset records occupancy rates for all council-managed car parks,collected from October 4, 2016 to December 19, 2016.The data is normalized to a 0-1 range for testing purposes.We use 10000 recent observations in our experiments,with 80%(8000)for training and 20% (2000) for testing, performing the same one-stepahead prediction.The Birmingham parking dataset is shown in Fig.8.

Fig.8.Birmingham parking dataset(first 1000 points).The x-axis coordinates represent the collection sampling points and the y-axis coordinates represent the Birmingham parking data.

Bike-sharing dataset Obtained from the UCI Machine Learning Repository,[42]this dataset contains the hourly number of bicycles rented in the bike-sharing system, collected from January 1, 2011 to December 31, 2012.We use 10000 recent observations in our experiments, with 80% (8000) for training and 20%(2000)for testing,performing the same onestep-ahead prediction.The Bike-sharing dataset is shown in Fig.9.

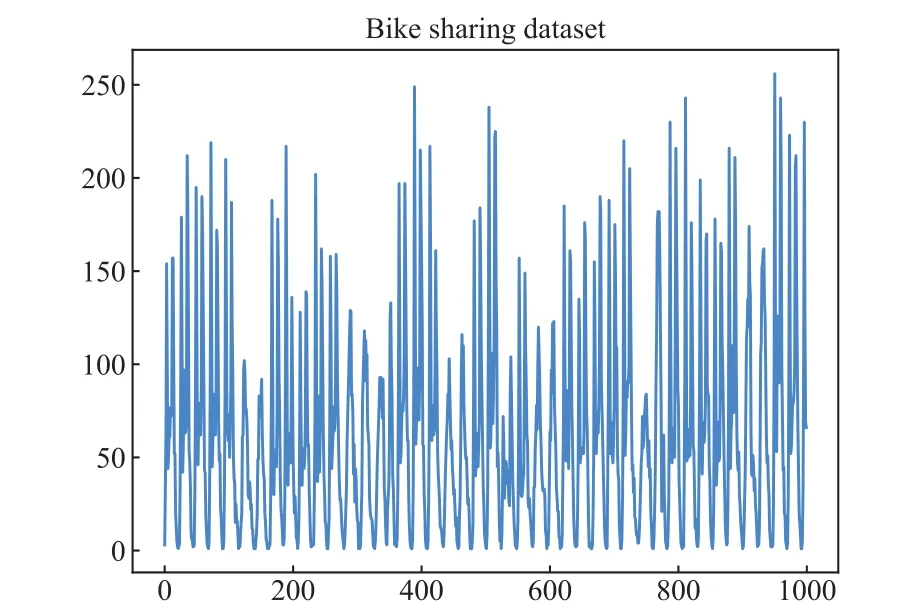
Fig.9.Bike sharing dataset(first 1000 points).The x-axis coordinates represent the collection sampling points and the y-axis coordinates represent the Birmingham parking data.

To ensure fairness in the experiments and to highlight the advantages of the dual random nanowire networks,all singlelayer ESN networks and layered ESN networks have the same number of training parameters for the output layer.The size of each reservoir layer is fixed at 300, a reasonable size that ensures both network performance and operational efficiency.All single-layer nanowire networks and layered nanowire networks have a fixed number of training parameters for the output layer of 100, with 15 nodes’ voltages serving as the intermediate state node voltages for data analysis.All singlelayer and layered models were compared,with the intermediate reservoir layer and output connections added to all models.

4.2.Evaluation metrics

It is important to note that there are two forecasting methods for long-term time series forecasting: iterative forecasting and direct forecasting.Iterative forecasting predicts subsequent values based on previous ones,while direct forecasting establishes a multi-step mapping relationship without iterating to obtain the result after multiple steps.The forecasting model can be expressed as follows:

The original ESN[43]used iterative prediction,which has higher accuracy than direct prediction.However, previous works[44-46]found that iterative prediction suffers from error accumulation, leading to instability when dealing with real-world nonlinear time series.Therefore, direct prediction is used in the experiments.Normalized mean square error (NMSE), mean absolute percentage error (MAPE) and normalized root mean square error (NRMSE) are employed to evaluate the prediction performance of each model.The NRMSE formula is as follows:

The closer the evaluation result is to 0, the higher the prediction accuracy.Here,Y(t)represents the target signal,y(t)denotes the prediction result after training andiindicates the number of time points.The MAPE formula is as follows:

whereY(t)is the target signal,y(t)is the prediction result after training andNdenotes the number of time points.The evaluation results range from percentage results,where an MAPE of 0% indicates a perfect model and an MAPE greater than 100% indicates an inferior model.The NMSE error formula is as follows:

The closer the evaluation result is to 0 indicates the higher prediction accuracy,whereY(t)is the target signal,y(t)is the prediction result after training andidenotes the number of times points.

4.3.Results

The performance metrics for various network models on the sunspot dataset are presented in Table 1.Additionally,Fig.10 compares the predicted and actual results of the layered ESN and DS nanowire network for a selected time step in the sunspot dataset.The DS nanowire network’s predictions are relatively smooth, with improved MAPE metrics, outperforming the layered ESN.Despite having fewer nodes than the ESN and using the node voltage of some nodes (15 nodes in this case) for model training, the DS nanowire network still achieves excellent real-time series prediction results.The DS nanowire network’s prediction index on the sunspot time series dataset is higher than that of the single-layer nanowire network,which is related to the dataset’s data quantity and model complexity.The DS nanowire network can overcome data quantity limitations and enhance prediction accuracy,demonstrating the rationality and superiority of a deep reservoir computing design approach based on nanowire networks for realtime series prediction.

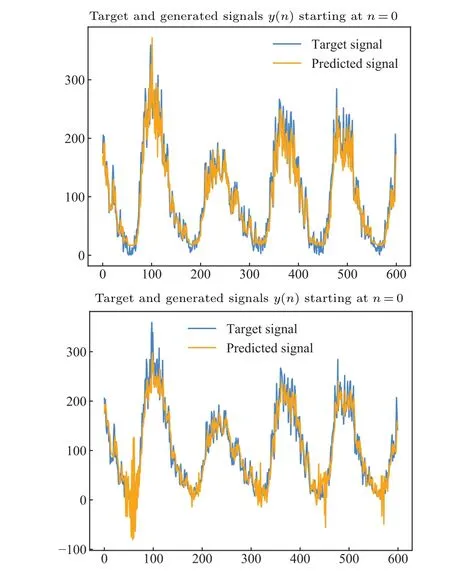
Fig.10.(a) Plot of the effect of the predicted results of the DS nanowire network model for predicting sunspot time series compared with the actual results.(b) Plot of the effect of the predicted results of the layered ESN model for predicting sunspot time series compared with the actual results.

Furthermore, Fig.11 compares the layered ESN and DS nanowire network’s prediction results for a selected time step in the Birmingham parking dataset and the actual results.During the prediction process, the layered ESN model may exhibit significant discrepancies between predicted and actual results.In contrast, the DS nanowire network model demonstrates smooth data point transitions,with minimal occurrence of unstable data prediction points.It consistently generates stable and accurate predictions at each prediction point, outperforming the hierarchical ESN in this aspect.

Fig.11.(a)Plot of the predicted results of the DS nanowire network model predicting the Birmingham parking dataset compared to the actual results.(b) Plot of the predicted results of the layered ESN model predicting the Birmingham parking dataset compared to the actual results.

Fig.12.(a) Plot of the predicted results of the DS nanowire network model predicting the bike-sharing dataset compared to the actual results.(b)Plot of the predicted results of the layered ESN model predicting the bike-sharing dataset compared to the actual results.

Additionally, Fig.12 compares the layered ESN and DS nanowire network’s prediction results for a selected time step in the bike-sharing dataset and the actual results.The DS nanowire network model not only achieves better accuracy but also ensures the stability of the prediction results.It possesses the flexibility to adapt to data variations, enabling the model to make accurate predictions in complex real-world environments.

According to Tables 1-3,the simulation results show that the three tables contain multiple models’ prediction metrics for the sunspot dataset, the Birmingham parking dataset and bike-sharing dataset.Combined with Figs.10-12,we will analyze the tables in detail from two aspects:prediction accuracy and data metrics analysis, and further explore the advantages of the DS nanowire network in terms of prediction stability,flexibility and robustness.

Prediction accuracy and data metrics analysis: prediction accuracy is an important metric for measuring the error between model predictions and actual observations.Based on the MAPE metrics in Tables 1-3, the DS nanowire network model demonstrates relatively high prediction accuracy across all three datasets.In Table 1,the DS nanowire network model has an MAPE of 0.685, which is lower compared to other models.In Tables 2 and 3, the DS nanowire network model has MAPE values of 0.248 and 0.873,respectively,which are also relatively low.This indicates that the DS nanowire network model can predict the target variable more accurately with smaller errors between the predicted and observed values.

Table 1.Performance of the DS nanowire network model with other prediction models on the sunspot time series.

Table 2.Performance of the DS nanowire network model with other prediction models on the Birmingham parking dataset.

Table 3.Performance of the DS nanowire network model with other prediction models on the bike-sharing dataset.

Prediction stabilityPrediction stability measures the consistency and stability of a model across different datasets.Based on the NARMSE and NMSE metrics in Tables 1-3,the DS nanowire network model has relatively low values, indicating smaller errors between the predicted and observed values and consistent performance across different datasets.This suggests that the DS nanowire network model has an advantage in prediction stability,producing stable and accurate predictions across different datasets.

FlexibilityFlexibility refers to the ability of a model to adapt to different datasets and problems.Based on the data metrics in Tables 1-3, the DS nanowire network model has lower model complexity compared to other models, making it easier to understand, implement and adjust.Its flexibility allows it to adapt to different datasets and problems,and it exhibits good generalization ability.This flexibility makes the DS nanowire network model more practical and scalable in real-world applications.

RobustnessRobustness refers to a model’s stability and adaptability to noise and variations in the data.Based on the prediction metrics in Tables 1-3, the DS nanowire network model demonstrates a certain level of robustness to noise and variations in the data.This means that it can generate reliable predictions in the presence of uncertainty and noise,showing good robustness.This enables the model to make accurate predictions in complex real-world environments.

The DS nanowire network model has advantages in prediction accuracy, prediction stability, flexibility and robustness.Its lower MAPE values indicate smaller errors between predicted and observed values,indicating higher prediction accuracy.Additionally,it has lower model complexity,making it easier to understand,implement and adjust,while also exhibiting good prediction stability and robustness.These advantages make the DS nanowire network model promising for practical applications and worthy of further research and exploration.

5.Conclusions

Self-organizing random nanowire networks can physically implement neuromorphic information processing and are a new approach to achieving neuromorphic computing and information processing.This study develops a model suitable for stochastic nanowire networks and observes the network’s overall dynamic behavior based on model simulations of network conductance changes and node voltage distribution over time.By leveraging the nanowire network’s characteristics of adaptive reallocation of node voltage and nonlinear voltage changes,information is encoded into voltages of different amplitudes and input into the nanowire network.The node voltage changes of each node over time are then collected as a reservoir state for reservoir computing.A scheme is designed to implement reservoir computing using the nanowire network for time information processing.Based on the nanowire network’s ability to process multiple spatiotemporal inputs, the DS nanowire network structure is proposed,providing a practical implementation scheme for the subsequent physical realization of deep reservoir computing based on nanowires.The single-layer nanowire network and the DS nanowire network’s prediction performance are tested on three real-time series datasets.The reservoir computing model based on the nanowire network achieves better prediction results than traditional deep reservoir computing.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos.U20A20227,62076208, and 62076207),Chongqing Talent Plan”Contract System”Project(Grant No.CQYC20210302257),National Key Laboratory of Smart Vehicle Safety Technology Open Fund Project (Grant No.IVSTSKL-202309), the Chongqing Technology Innovation and Application Development Special Major Project(Grant No.CSTB2023TIAD-STX0020),College of Artificial Intelligence,Southwest University,and State Key Laboratory of Intelligent Vehicle Safety Technology.