Effect of electron–electron interaction on polarization process of exciton and biexciton in conjugated polymer

Xiao-Xue Li(李晓雪), Hua Peng(彭华), Dong Wang(王栋), and Dong Hou(侯栋)

1School of Physics and Technology,University of Jinan,Jinan 250022,China

2Jinan Institute of Quantum Technology,Jinan 250101,China

Keywords: conjugated polymer,exciton,electron-electron interaction,reverse polarization

1.Introduction

Owing to the fact thatπ-conjugated polymers such as polyacetylene possess abundant optical-electrical characteristics,more and more researchers have paid attentions to them in the past decades.The conjugated polymers have been regarded as the most potential organic semiconductor materials,and the theoretical investigation on them involves the interdisciplinary area of physics, chemistry and material science.In terms of technological applications, the conjugated polymers have been widely used to fabricate diverse organic optoelectronic devices, such as organic light emitting diodes (OLEDs),[1,2]organic photovoltaic cells(OPVs),[3,4]and organic field effect transistors(OFETs).[5,6]

Being different from the conventional inorganic semiconductors, the organic polymers possess the quasi-onedimensional structure, and the electron-phonon coupling in them is strong.For this reason, under the effect of nonneglectable electron-lattice interaction, the extra electronhole pair introduced by photoexcitation can easily distort the lattice configuration of polymers,and then the self-trapped elementary excitations are formed,such as excitons and biexcitons.It is proposed that the light principle of OLED originates from the processes of electroluminescence and photoluminescence in organic semiconductors, which are thought to be related to these elementary excitations.For this reason, during the past decades, lots of efforts have been devoted to exploring the processes of formation, polarization and dissociation of elementary excitations in polymers.[7-36]

For example, by using the famous one-dimensional Su-Schrieffer-Heeger (SSH) model in the tight-binding approximation, Sunet al.[7]and Fuet al.[8]theoretically investigated the polarization of exciton and biexciton under the effect of external electric field.They found that the exciton is normally polarized, and the biexciton is reversely polarized.So they predicted that the polarization in polymers can be reversed when an exciton absorbs one photon to form biexciton.They referred to this new photoinduced phenomenon as photoinduced polarization inversion (PIPI).Wanget al.explored the stability of PIPI phenomenon under the effects of both atomic disorder and chain length.[9,10]Both square model and Gaussian random model have been used to simulate the atomic disorder.Gaoet al.discussed the effect of interchain coupling on the reverse polarization of a biexciton.[11]However,in the above researches,due to the limitation of theoretical method, only static polarization property was presented.Through self-consistently solving the static Schr¨odinger equation and the equilibrium condition of lattice configuration,the total energy of the system is minimum.Since the adiabatic or non-adiabatic dynamical evolution method has not been used,the calculated results are not related to the temporal evolution of polarization, let alone its dynamical inversion.Although PIPI was first proposed by Sunet al.,the inversion process has not been presented effectively.

In their researches, Chenet al.also mentioned that a reverse polarization might appear in aπ-conjugated polymer chain with a charged polaron through a single-photon excitation.[12]According to this,Gaoet al.theoretically investigated the single-photon excitation in a charged oligomer.[13]They pointed out that after the single-photon absorption, the excited polaron is reversely polarized.We theoretically investigated the effect of interchain coupling on the formation and polarization of the single-excited state of polaron in conjugated polymers,[14]and explored the effect of electronelectron interaction on the polarization of the single-photon excited state of the chargedπ-conjugated oligomer.[15]

In 2004, through “by-hand” exciting one electron from a low occupied molecular orbital to high empty one, Anet al.investigated the single-electron transition in a polymer.[16]It was found that the transition from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital(LUMO)results in an exciton,while the transition from below-HOMO to above-LUMO leads to the formation of a high-energy exciton.In 2009, by using the femtosecond pulsed electric field to simulate the photoexcitation, Gaoet al.explored the band-edge transition process and the nonband-edge transition process of electron in polymer.[17]They pointed out that it is difficult to realize PIPI via a sequential excitation.This means that the formation of high-energy exciton is easier than biexciton.In 2011,we studied the polarization of a high-energy exciton in conjugated polymers.[18]We pointed out that the high-energy exciton (the non-band-edge singlephoton excited state)can also be reversely polarized.In 2014,we further studied the effects of non-degenerate confinement,electron-electron interaction, and interchain coupling on the reverse polarization of the high-energy exciton.[19]Since then,we have noted that the reverse polarization, which is an essential condition for the realization of PIPI,can be seen in an increasing number of elementary excitations,as well as biexction.However,if the research method has not been improved,the dynamical inversion process cannot be visually exhibited.

It should also be noted that in the above researches, the electron-electron interaction has been taken into account,and then the spin-related term can be introduced into the system so as to break the spin degeneracy.[15,19]However,only the effect of electron-electron interaction on the static polarization property of elementary excitations in polymer has been presented.Through the self-consistent iteration process,the total energy of system is minimized,but when does the polarization begin to appear or reach the maximum? Once the excitons or biexcitons are finally dissociated by the strong electric field,does the electron-electron interaction affect the dynamical evolution processes? These questions have not been involved in the above researches.So it is difficult for us to confirm whether the electron-electron interaction can significantly affect the processes of formation, polarization and dissociation of elementary excitations in polymers.

From the above-mentioned researches we do not know Under the action of electron-electron interaction,whether the polarization is enhanced or inhibited, nor whether the critical value of electric field strength at which the dissociation process occurs is increased or decreased,nor whether the PIPI(or at least polarization inversion) is actually obtained or not.In addition,with spin multiplicity considered,the singlet state of exciton and the triplet can be distinguished from each other.Under the same external conditions, it is unclear whether the effect of electron-electron interaction on their polarization and dissociation processes is the same.

In this work,by using both the modified SSH model with taking the electron-electron interaction into consideration,and the non-adiabatic dynamical evolution method, we simulate the processes of polarization and dissociation of singlet exciton, triplet exciton, and biexciton under the action of electric field.It is expected that the polarization inversion process(which is an indispensable part of PIPI phenomenon),even the inversion of spin,can be visually realized.The rest of this paper is organized as follows.In Section 2, we give the model and method.The results and discussion are presented in Section 3.Finally, some conclusions are drawn from the present study in Section 4.

2.Theoretical methods

We consider cis-polyacetylene with non-degenerate ground-state structure, and establish the Hamiltonian in the form of

the intrachain hopping integral between sitesnandn+1.In Eq.(3),trepresents the nearest-neighbor transfer integral for a uniform bond structure in the case of non-dimerization,αthe electron-lattice coupling constant, andun(t) the timedependent displacement coordinate ofn-th carbon atom from its equilibrium position.The Brazovskii-Kirova symmetry breaking term with parameterteis introduced in order to remove the ground-state degeneracy of polyacetylene withcisconfiguration rather than trans.[40]In Eq.(2),C+n,sandCn,sare the creation operator and the annihilation operator of electron with spinsat siten,respectively.The second term denotes the elastic potential energy with elastic constantK.The third term classically describes the kinetic energy of lattice atoms withMdenoting the mass of Carbon-Hydrogen group.

denotes the interaction energy between electron and electric field.Here,eis the electron charge,Nthe total number of lattice sites in an isolated polyacetylene chain, andathe lattice constant.We choose the center of chain as the zero potential energy reference point.The electric field is applied along the chain so as to polarize or dissociate exciton and biexciton withE(t) the time-dependent field strength.In order to avoid the sudden disturbance to lattice configuration,we use the electric field through a smooth turn-on process in the form of half-Gaussian function,

denotes the electron-electron interaction in the form of the extended Hubbard model in the Hartree-Fock approximation.[41]Here,Udenotes the Coulomb repulsion interaction strength between two on-site electrons with opposite spin orientations,sand-s.The orientation of spinsis up or down(denoted by↑or↓).

In the Wannier representation, the time-dependent electronic state|〉on theµ-th energy level is expanded into

wherefµ,s(0 or 1) is the time-independent initial occupied number of electrons on theµ-th energy level with spins.

The temporal evolution of lattice displacementun(t) is described by the classical Newton equation of motion

is the spin-dependent total density matrix.By using the eighth order Runge-Kutta method with step-size control,[42]we calculate numerically the coupled differential equations (8) and(10).

3.Results and discussion

We choose the parameters of cis-polyacetylene in the SSH model ast=2.5 eV,α=4.1 eV/°A,te=0.05 eV,K=21 eV/°A2,andM=1349.14 eV·fs2/°A2.[37-39]The calculated results are expected to be qualitatively valid for other conjugated polymers with non-degenerated ground-state structure.In Eqs.(4) and (5), we setN=100,a=1.22 °A,tc=75 fs,tw=25 fs,and the time step Δt=1 fs.

For better visualization, we introduce the smoothed lattice configuration

To facilitate the analysis, we schematically demonstrate the occupation of electrons on energy levels in Fig.1.Here,εvµdenotes theµ-th energy level counted from the top of valence band, andεcµtheµ-th from the bottom of conduction band.Figure 1(a) shows that in the ground state, the conduction band is empty, and the valence band is fully filled.Each level of valence band is occupied by one electron with spin up(denoted by red up arrow),and one electron with spin down (denoted by the blue down arrow).Figure 1(b) shows that after single-photon absorption, one electron with spin up(or down) is excited fromεv1toεc1, and then the singlet exciton is formed.Figure 1(c)displays that for the triplet exciton,the spin orientation of electron onεv1andεc1are parallel as displayed in Fig.1(c).After double-photon absorption, two electrons are excited fromεv1toεc1, and then the biexciton is formed as indicated in Fig.1(d).

Fig.1.Schematic diagram of energy levels for polyacetylene molecule in(a) ground state, (b) singlet exciton state, (c) triplet exciton state, and (d)biexciton state.

which represents the dipole moment ofπ-electron.We build the 1D coordinate system along the polymer molecule chain,and choose its center as the zero point.As the positive ion core on each Carbon-Hydrogen group of polymer molecule possesses one unit charge, the dipole moment of lattice atomPl(t)=0.

3.1.Effect of electron–electron interaction on polarization of singlet exciton

Figure 2(a) shows the temporal evolution of dipole moment under the action of electric field with medium strength ofE=5 mV/°A.In the case ofU=0,the red line shows that the dipole moment of normally polarized singlet exciton smoothly increases from zero in the same form of half-Gaussian function as the strength of electric field.At the turn-on period oftc=75 fs, the dipole moment reaches its maximum value ofPe=2.4|e|·°A.In the case ofU=0.5 eV, the black line shows that the singlet exciton can still be normally polarized at the beginning.However, when the dipole moment reaches the maximum value att ≥tc, it is no longer constant, and an obvious dipole oscillation appears betweenPe=-5.7|e|·°A andPe=9.3|e|·°A.

Fig.2.Temporal evolution of(a)dipole moment and(b)occupied number of electron at E=5 mV/°A for singlet exciton.

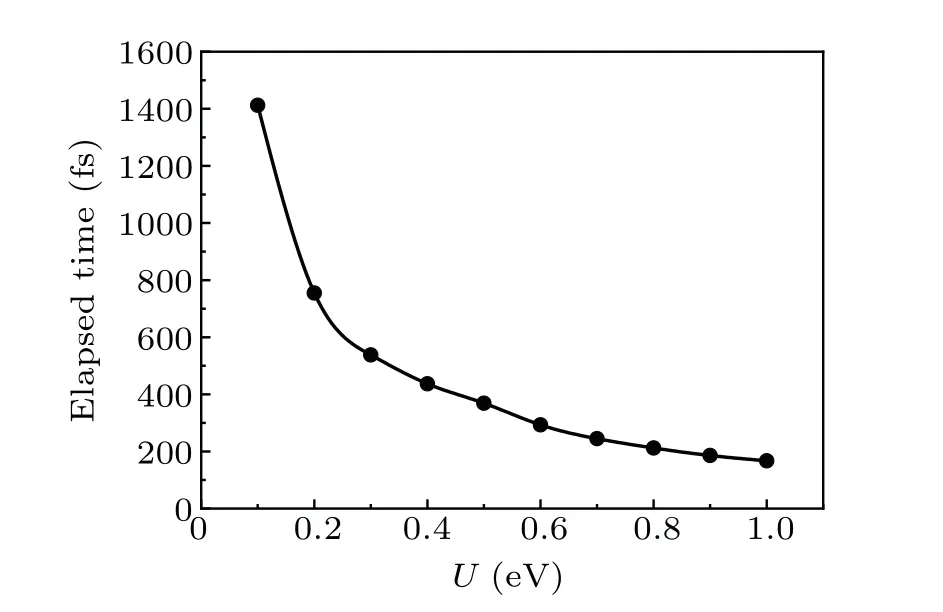
Fig.3.Dependence of elapsed time on electron-electron interaction strength at E=5 mV/°A for singlet exciton.

When the electron is completely transferred from the occupied energy level to the unoccupied energy level,it is worth studying whether it becomes stable and remains stable at the new-occupied energy level In Fig.4, we calculate the occupied number of electrons on deep energy levels with evolution time increasing.As shown in the figure, after the newoccupied level is completely occupied, the electron on it is no longer stable.A new round of transition from the newoccupied (initially unoccupied) level to the new-unoccupied(initially occupied)level occurs.The cycle repeats itself,and then the electron transfers back and forth between high and low deep levels,with theirQvalues changing periodically.We also find that with the enhancement of electron-electron interaction strength, oscillation period decreases.Figure 4 shows that when the strength of electron-electron interaction is weak,e.g.,U=0.3 eV,at the end of each period,the number of electrons on deep level is nearly no changed compared with its initial value before oscillation.As is mentioned above,it demonstrates that the singlet exciton is stable at the weak strength.

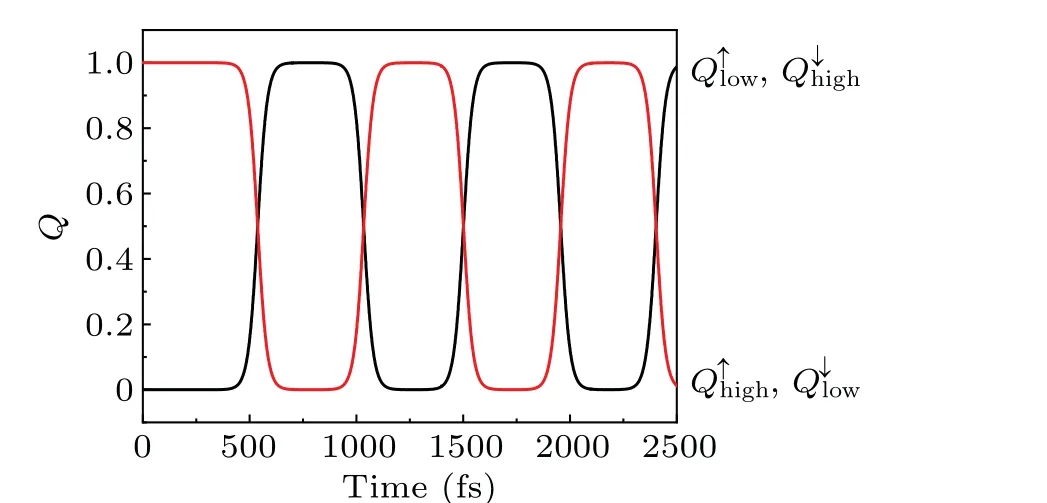
Fig.4.Temporal evolution of occupied number of electrons at E=5 mV/°A and U =0.3 eV for singlet exciton.

Fig.5.Temporal evolution of(a1)-(a3)lattice configuration and(b1)-(b3)charge density of singlet exciton at(a1)-(b1)E =5 mV/°A and U =0,(a2)-(b2)E=9.2 mV/°A and U =0,and(a3)-(b3)E=5 mV/°A and U =1 eV.

What happens when the interaction is enhanced?Figure 5 shows the dynamical evolution of lattice configuration and charge density distribution of singlet exciton under the action of electric field before and after introducing electron-electron interaction.In the case ofE=5 mV/°A andU=0,figure 5(a1)shows that the singlet exciton is steadily localized in the center of chain.In the moderate field, it is normally polarized, with its positive charge(the red region in Fig.5(b1))distributed on the right side of lattice distortion, and negative (blue) on the left.In order to dissociate it, the field strength must be increases.In the case ofE=9.2 mV/°A andU=0,figure 5(a2)shows that the singlet exciton is stable for no more than 150 fs.The irregular lattice vibration of surrounding background it is dissociated into carrier pair.In the strong field, the positive charge(denoted by red in Fig.5(b2))rapidly agglomerates on the right end of polyacetylene chain, and the negative (blue)on the left.Is this the only way to dissociate the singlet exciton? In the case ofE=5 mV/°A andU=1 eV, figure 5(a3)shows that the localization of singlet exciton becomes weak att=100 fs.The lattice distortion oscillates in the center of chain tillt= 950 fs.Ultimately, the singlet exciton is dissociated into the positive carrier (localized in right chainend), and the negative carrier(localized in left chain-end), as shown in Fig.5(b3).It is demonstrated that the enhancement of electric field is not the only way to dissociate the singlet exciton.As the above results show,in the moderate field,the final state of singlet exciton can change from norma polarization without the on-site electron-electron Coulomb repulsion to dissociation into carrier pair when the interaction strength is strong enough.The stronger the electron-electron interaction,the earlier the dissociation of singlet exciton occurs.On account of ultimate chain-end accumulation of carrier,the dipole moment reaches its maximum value.Since then, it has been roughly constant.

Fig.6.Dependence of dipole moment on electron-electron interaction strength at E ＞Ec after dissociation of singlet exciton.

With the increase of electron-electron interaction strength,the critical value of electric fieldEc,at which the singlet exciton is dissociated, decreases.We calculate the value of dipole momentPeafter dissociation of singlet exciton under different values of interaction strengthUatE ＞Ec, and the results are given in Fig.6.As shown in the figure,Pedecreases almost linearly with the increase ofU.It is indicated that the singlet exciton is not completely dissociated into carrier pair, and there may generate other states.Otherwise,Peis constant whenUchanges.We guess that the yield of these states besides carrier pair may increase with the enhancement of electron-electron interaction.So,now,the problem is what these other states are.

Fig.7.Temporal evolution of occupied number of electron at(a)E=5 mV/°A and U =0,(b)E=9.2 mV/°A and U =0,and(c)E=5 mV/°A and U =1 eV for singlet exciton.

Fig.8.Schematic diagram of electron occupation on intra-gap energy levels after dissociating singlet exciton.

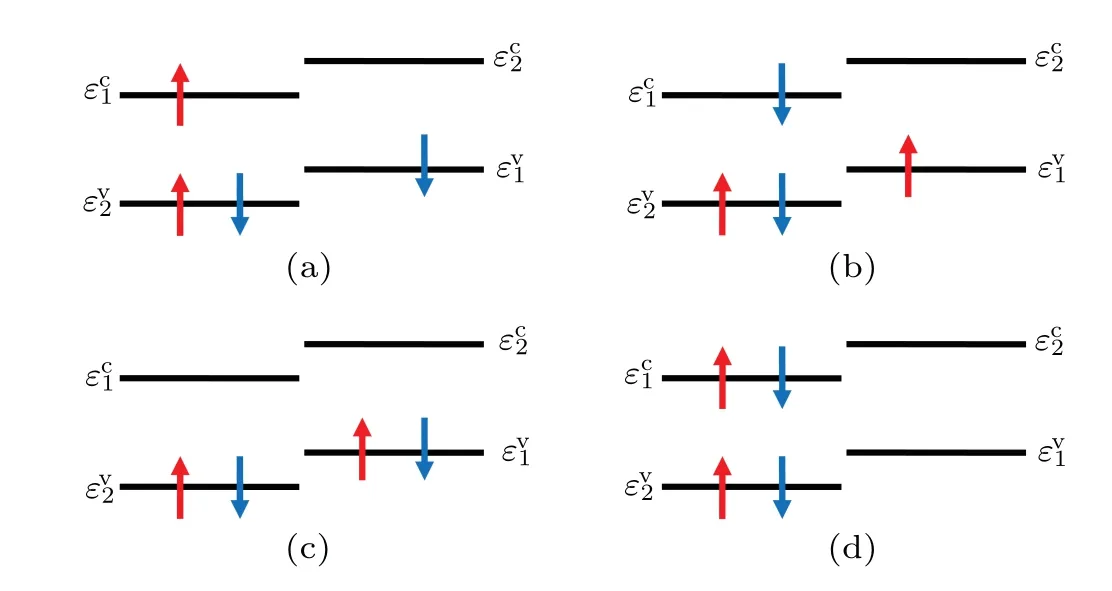
Fig.9.Possible states formed after dissociating singlet exciton.

Under the action of electron-electron interactions with different strengths, the spin distribution can be reversed as ¯Qchanges.It depends on which state in Figs.9(a)and 9(b)has higher yield.Figure 10 show the spin evolution ¯Sn(t) of polaron that originates from the dissociation of singlet exciton atE=3.5 mV/°A.It is found that with the increase of electronelectron interaction strength fromU=0.7 eV to 1.0 eV, the spin distribution flips.AtU=0.7 eV, the polaron with spin up (the red region) is located on the left side of chain, and the polaron with spin down (blue) on the right side.While atU=1.0 eV, the situation is completely opposite.By calculating and analyzing ¯Q, we obtain that the yields of state in Fig.9(a) significantly decreases from 54.99% to 1.38%,and the yield of state in Fig.9(b)significantly increases from 2.87%to 55.9%.The net spin distribution is from up to down along the chain with the yield of 52.12% atU=0.7 eV, and from down to up with the yield of 54.52%atU=1.0 eV.Then we conclude that through modulating the strength of electronelectron interaction,we could observe the spin-flip of polaron pair dissociated from the singlet exciton.

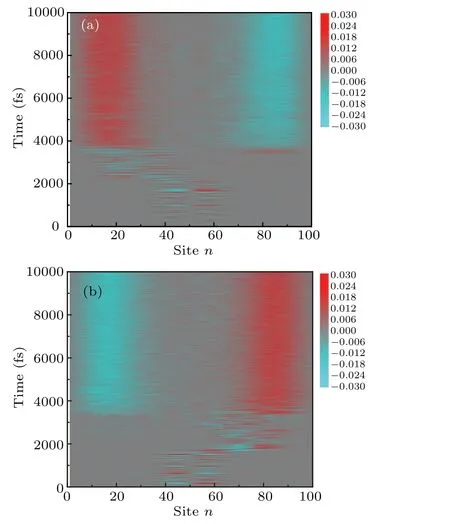
Fig.10.Temporal evolution of spin distribution after dissociating singlet exciton at E=3.5 mV/°A with(a)U =0.7 eV and(b)U =1 eV.

3.2.Effect of electron–electron interaction on polarization of triplet exciton.

Next, we explore the effect of electron-electron interaction on polarization of triplet exciton,and the results are given by blue line in Fig.2(a).As can be seen from the figure, the normal polarization of triplet exciton can also be obtained.Instead of alternation between positive and negative value, its dipole moment hovers around 2|e|·°A.As shown in Fig.1(c),for triplet exciton,there is one electron occupied on each of the band-edge energy levelsεc1andεv1,respectively,with the same spin orientation.According to the Pauli exclusion principle,it is impossible for the transition of electron between valence band and conduction band to occur.As the occupied number is unchanged,the normal polarization of triplet exciton under the action of electric field is stable,although the electron-electron interaction has been intervened.The obvious dipole oscillation is replaced by small fluctuation.As there is no electron transition,at the sameEandU,the polarization of triplet exciton is more stable than that of singlet.

We calculate the mean value of dipole moment ¯Peafter the polarization of triplet exciton has become stable in a moderate electric field ofE=5 mV/°A, and show its dependence on the strength of electron-electron interaction in Fig.11.As can be seen in the figure, the dipole moment decreases linearly with the increase of strengthU, which means that the electron-electron interaction can restrain the polarization of(triplet) exciton.It seems to be inconsistent with the conclusion obtained by Sunet al.[7]and Fuet al.[8]In their researches, they pointed out that the on-site Hubbard energyUobviously increases the polarization of self-trapping excited state, which originates from the excitation of one photon.As there is no spin-related term in Hamiltonian of their systems,the spin of electron is a conserved quantity.The spin degeneracy is not broken, and then the formed exciton cannot be distinguished between singlet and triplet.In fact, as there is no spin-flip nor spin precession of electron when it transfers from the valence band to the conduction band through singlephoton absorption,according to the Pauli exclusion principle,the formed single-excited state is singlet exciton, rather than the triplet we explore here.In addition, due to the limitation of research method, their conclusion is based on the calculation of static polarization property of exciton, rather than the further exploration of its dynamical evolution as done in our work by using the non-adiabatic method.

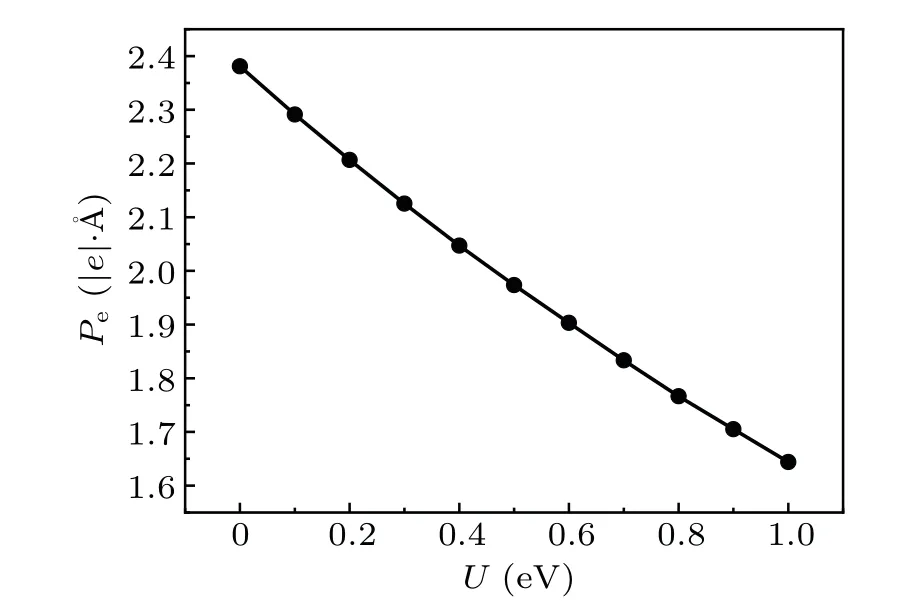
Fig.11.Dependence of mean value of dipole moment on electron-electron interaction strength after the triplet exciton has been polarized at E =5 mV/°A.

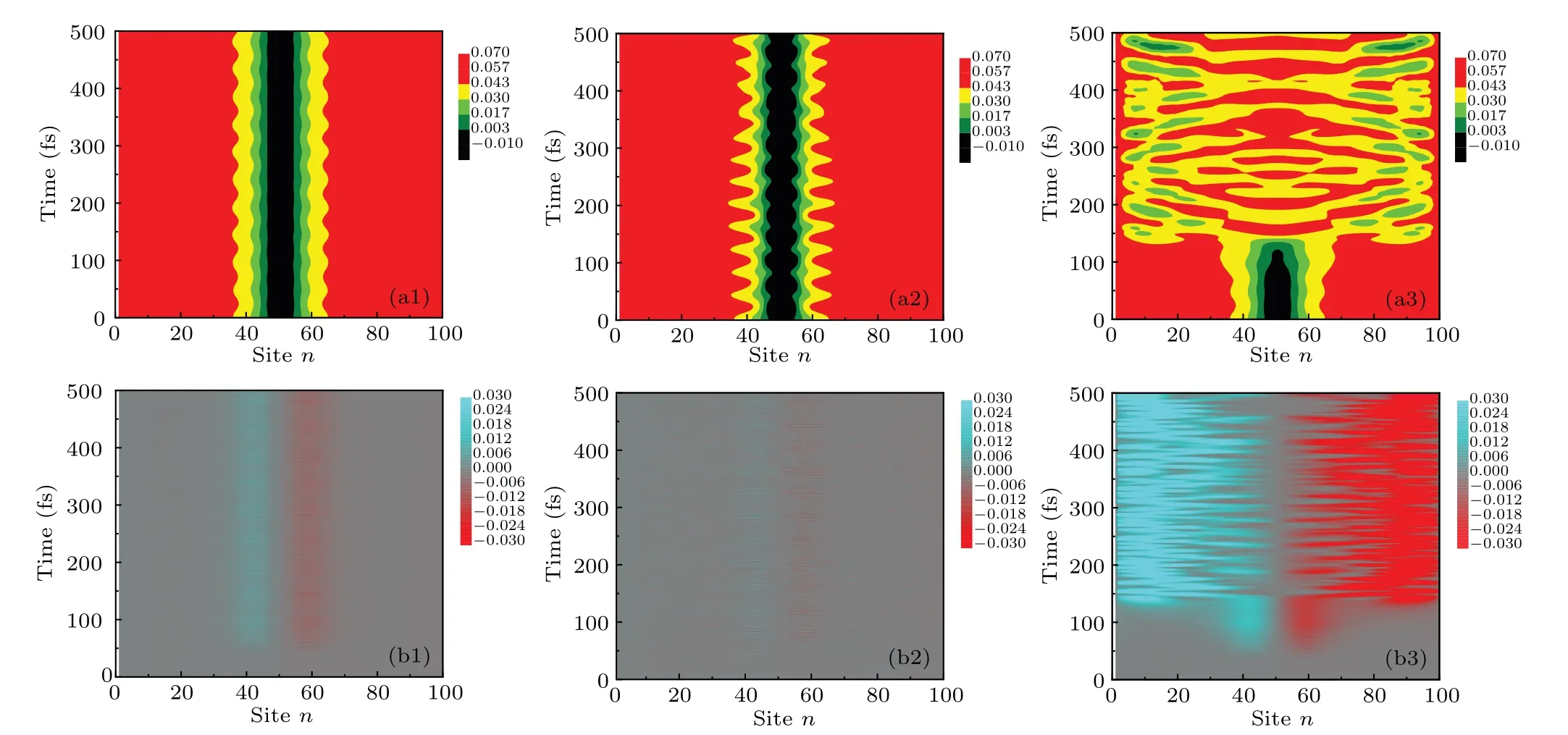
Fig.12.Temporal evolutions of (a1)-(a3) lattice configuration and (b1)-(b3) charge density of triplet exciton at (a1)-(b1) E =5 mV/°A and U =1 eV,(a2)-(b2)E=5 mV/°A and U =4 eV,and(a3)-(b3)E=11 mV/°A and U =1 eV.

Figure 5 shows that the singlet exciton can be dissociated not only in a strong electric field but also in a moderate electric field ofE=5 mV/°A.The premise is that the electron-electron interaction is included with the strength up to 1eV.While in the case of the triplet exciton,the situation is completely different.Figure 12 shows the dynamical evolution of lattice configuration and charge density distribution of triplet exciton under the action of electric field after having introduced electronelectron interaction.In the case ofE=5 mV/°A andU=1 eV,Figs.12(a1) and 12(b1) show that the triplet exciton is still stably and deeply located in the center of the chain and is normally polarized.In comparison with the singlet exciton,under the same condition, the stability of triplet exciton is significantly improved.Then, there appears the problem of how to dissociate it.We must ascertain whether the electron-electron interaction has been enhanced or whether the electric field has been strengthened.In Figs.12(a2)and 12(b2),we increaseUto 4 eV,and amazingly,we find that the triplet exciton can still be stable.Under the action of so strong interaction,the locality of triplet exciton is enhanced.Its normal polarization is obviously weakened, although the strength of electric field is unchanged.The singlet exciton can be dissociated in a moderate electric field by strengthening the electron-electron interaction,but triplet exciton cannot.We have to adopt the original method, i.e.by increasing the strength of electric field.Figures 12(a3)and 12(b3)show the results atE=11 mV/°A andU=1 eV.It can be found that the field is so strong that the triplet exciton is ultimately dissociated.

3.3.Effect of electron–electron interaction on polarization of biexciton

Finally,we explore the effect of electron-electron interaction on polarization of biexciton at the moderate electric field ofE=5 mV/°A,and the results are given in Fig.13.From the figure it may follow that with the electron-electron interaction included,the reverse polarization of biexciton can be obtained.This situation is quite different from the singlet exciton that an obvious oscillation of dipole moment between positive and negative value is presented atU ̸=0.We calculate the mean value of dipole moment ¯Pe, which is more than several hundreds of femtoseconds after the polarization of biexciton has been stable, and explore the effect of electron-electron interaction strength on it.The linear relationship between them is obtained,which is similar to the results of triplet exciton in Fig.11.However,unlike the triplet exciton with its normal polarization restrained,the reverse polarization of biexciton can be enhanced by electron-electron interaction.It is consistent with the conclusion obtained from Refs.[7,8].

Fig.13.Temporal evolutions of dipole moment at E=5 mV/°A for the biexciton.

Fig.14.Temporal evolutions of (a1)-(a3) lattice configuration and (b1)-(b3) charge density of biexciton at (a1)-(b1) E =5 mV/°A and U =0, (a2)-(b2)E=15 mV/°A and U =0,and(a3)-(b3)E=5 mV/°A and U =4 eV.

Figure 14 shows the dynamical evolution of lattice configuration and charge density distribution of biexciton in a moderate electric field and strong electric field before and after introducing electron-electron interaction, respectively.In the case ofE= 5 mV/°A andU= 0, figure 14(a1) shows that the lattice distortion of biexciton is located in the center of the chain.It is reversely polarized, i.e., the positive charge(red region) is trapped in the left part of lattice distortion,and the negative charge (blue region) in the right, which are shown in Fig.14(b1).The origin of reverse polarization of biexciton has been revealed in Refs.[7,8].Before introducing electron-electron interaction,we have to enhance electric field toE=15 mV/°A so as to dissociate the biexciton, the results are shown in Figs.14(a2) and 14(b2).In the case ofE=5 mV/°A andU=4 eV, figures 14(a3) and 14(b3) show that the biexciton is no longer localized with the time going by in about 2000 fs.Finally, two shallow lattice distortions are formed on the two sides of chain-end.In this process,the positive charge initially trapped in the left region of lattice distortion of biexciton instantly jumps to the right side of chainend at about 2000 fs, while the negative charge in the right region jumps to the left side.In the moderate electric field,the strong electron-electron interaction can not only dissociate the biexciton,but also flip the charge distributed along the chain.After including the electron-electron interaction, the critical value of electric fieldEc,in which the biexciton is dissociated,decreases significantly.

Fig.15.Temporal evolutions of occupied number of electrons at E =5 mV/°A and U =4 eV for biexciton.

Fig.16.Schematic diagrams of electron occupation on intra-gap energy levels after dissociating biexciton.

Fig.17.Possible states formed after dissociating biexciton.

4.Conclusions

In this work, we explored the effect of electron-electron interaction on polarization of(singlet and triplet)exciton and biexciton in 1D cis-polyacetylene chain by adopting tightbinding SSH model and non-adiabatic method.It is found that in a moderate electric field ofE=5 mV/°A, the on-site electron-electron Coulomb repulsion being taken into consideration, an obvious dipole oscillation of singlet exciton appears, when the interaction strength is weak.The electron located on deep levels becomes unstable and transfers back and forth between them periodically, but the singlet exciton is stable.When the interaction strength is strong enough, the singlet exciton is dissociated into carrier pair.The stronger the electron-electron interaction,the earlier the dissociation of singlet exciton occurs.Thus it can be seen that the enhancement of electric field is not the only way to dissociate the singlet exciton.In addition, through modulating the strength of electron-electron interaction, we can observe the spin-flip of polaron pair dissociated from the singlet exciton.In the case of triplet exciton, the mean value of its dipole moment after the polarization has become stable decreases linearly with the enhancement of electron-electron interaction.Under the same condition,the stability of the triplet exciton is significantly improved compared with that of the singlet exciton.For example,in a medium field ofE=5 mV/°A, the singlet exciton is dissociated by strengthening the electron-electron interaction toU=1 eV, while the triplet exciton is not dissociated.When the interaction strength increases toU=4 eV, the triplet exciton is still stable and its locality is enhanced, although its normal polarization is obviously weakened.We can enhance the strength of electric field in order to dissociate it.In the case of biexciton, its reverse polarization is enhanced by increasing the interaction strength.When the strength is strong enough, not only is the biexciton dissociated, but its charge distribution is also flipped.In addition,we analyzed the possible states formed after dissociating(singlet and triplet)exciton and biexciton,and calculate the yields at different strengths of electron-electron interaction.

Acknowledgement

Project supported by the Natural Science Foundation of Shandong Province,China(Grant No.ZR2020MA070).