MSK-LFM一体化信号波形相关性分析与参数选择

杨 铭,高 猛

(空军通信士官学校,辽宁 大连 116600)

雷达通信一体化波形共用技术旨在通过一种信号同时实现信息传输和目标探测两个功能,以此降低电子设备冗余度,避免设备间干扰,提高频谱利用率,是雷达通信一体化领域的热点研究方向。文献[1-4]一体化波形设计分为两种方式:一是基于通信信号实现雷达功能[5];另一种是将通信数据调制到雷达信号上,在探测的同时完成数据的发送[6-7]。目前,脉冲体制雷达的主用波形为线性调频信号(Linear Frequency Modulation, LFM)[8-10],而最小频移键控(Minimum Shift Keying,MSK)调制方式以其包络恒定、相位连续、频谱效率高等优点成为将通信数据调制到LFM脉冲信号上的主要方式[11]。

本文基于二进制数字信号的最佳接收理论,构建了MSK-LFM信号中初始频率、调频率、码元周期等参数和波形相关系数、码元能量之间的数学模型,通过数值仿真拟合了相关系数与各参数的变化关系。在此基础上,构建MSK-LFM相关接收模型,并选取不同参数对理论模型进行了仿真验证。仿真结论表明通过合理选择MSK-LFM信号参数,可改善通信误码率性能。

1 MSK-LFM信号的产生原理

MSK调制是连续相位调制CPM一种特定形式,各码元之间具有连续的相位变化。同时利用不同的频率代表不同码元,本质上也属于2FSK调制。在采用单频率正弦波作为载波时,通过合理确定传、空号码元对应的频率差,将MSK调制的单载频换为LFM信号,即可得到MSK-LFM一体化信号,由此可得信号的表达式为

(1)

式中:fc为LFM信号初始频率;Tb为码元周期;u为调频率;ak为第k个码元的调制信息(传号时取“1”,空号时取“-1”);Tp=nTb为LFM脉冲信号的时宽;n为单个LFM脉冲中调制码元的个数;φk为第k个码元所对应波形的初始相位。

为保持共享信号相位连续,φk应满足:

(2)

为便于分析,取φ1=0,则φk=0或π。

2 MSK-LFM一体化信号误码率影响因素分析

根据二进制数字信号的最佳接收理论,在高斯白噪声信道下系统误码率Pe可表示为[16]

(3)

其中:

(4)

式中:表示噪声的方差;s0(t)为空号时的信号波形;s1(t)为传号时波形。式(3)(4)表明,误码率取决于不同码元时波形差异。将式(4)右端展开:

(5)

式(5)中ρ为传、空号波形的相关系数,是码元波形差异性定量描述,表示为

(6)

式中,E1、E0分别表示传、空号时波形的码元能量。

由式(5)可知,误码率取决于E1、E0和ρ的大小。而当采用LFM信号作为载波时,LFM信号的初始频率fc、码元周期Tb、调频率u等参数发生变化时,又必然影响E1、E0和ρ的取值,因此必须对上述参数之间的关系进行定量分析。

2.1 含时间平方项三角函数积分的计算

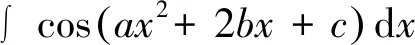
(7)

式中,a、b、c为常量,C(·)、S(·)为菲涅尔积分,其具体定义式为

(8)

利用MATLAB提供的fresnels(…)和fresnelc(…)函数,可得到函数值随自变量的变化曲线如图1。由图可见,C(·)、S(·)的值随自变量的增加振荡收敛于0.5。

图1 菲涅尔积分变化曲线

2.2 码元能量变化规律分析

现仅考虑脉冲内调制的第1个码元(0≤t≤TB),并假设载波初相位为0,由式(1)(6)可得:

(9)

利用式(7),令a=2πu、b=2πf1、c=0,则式(9)变为

(10)

同理可得E0为

(11)

图2 码元能量E1随初始频率f1变化曲线(u=0.2MHz·μs-1)

图3 码元能量E1随调频率u变化曲线

(12)

2.3 相关系数变化规律分析

由式(6)可知,ρ与信号振幅无关,但与单位振幅时码元能量有关。仍以第1个码元为例,对式(6)右端分子展开计算,有:

(13)

式(13)中右侧第二项为单频载波MSK调制时的计算结果,积分后为0,说明MSK两种码元对应波形具备正交性。然而,将单载频替换为LFM波形后,多出等式右端第一项。当其数值不为零时,必然会破坏码元之间正交性,从而影响通信误码率。仿照式(10)展开,同时将式(10)(11)(13)代入式(6)即可得到ρ的表达式。

取Tp=100μs,脉冲带宽Bp=20MHz,则u=0.2 MHz·μs-1,得到ρ随fc、n的变化关系如图4。由图4可见,fc越小、n越大,则ρ越大。在此仿真参数下最大值可达0.15左右,达到一个不可忽略的数值。

图4 相关系数ρ随初始频率fc、码元个数n的变化关系

为更直观对比,其他参数不变,n分别取100、200、400时,得到ρ随fc变化曲线如图5。

图5 相关系数ρ随初始频率fc变化关系

取n=100,得到在不同fc下ρ随u的变化曲线如图6。

图6 相关系数ρ随调频率u变化关系

由图可见,ρ随u变化时波动较小。但是,由式(1)可推导MSK-LFM信号第k个码元的初始频率为

(14)

式(14)说明增加u可以间接增加各个码元的初始频率,从而减小码元相关系数。

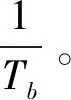
3 仿真验证

根据式(1)(2),得到MSK-LFM一体化信号的正交形式表达式:

(15)

式中,pk=cosφk,qk=akcosφk。基于此建立MSK-LFM一体化信号产生原理图如图7。图中ak经差分编码后得到序列bk,在串并转换后得到两个码元分支序列b2k-1和b2k,两路码元周期均为2Tb。上支路码元序列b2k-1可直接作为pk,下支路序列b2k延迟Tb后得到qk。

图7 MSK-LFM一体化信号产生原理图

假定信号无多普勒频偏且同步已完成,发射信号s(t)经高斯白噪声信道后到达接收端的信号为r(t)。接收端采用相关接收方法对MSK-LFM进行解调。接收机框图如图8。

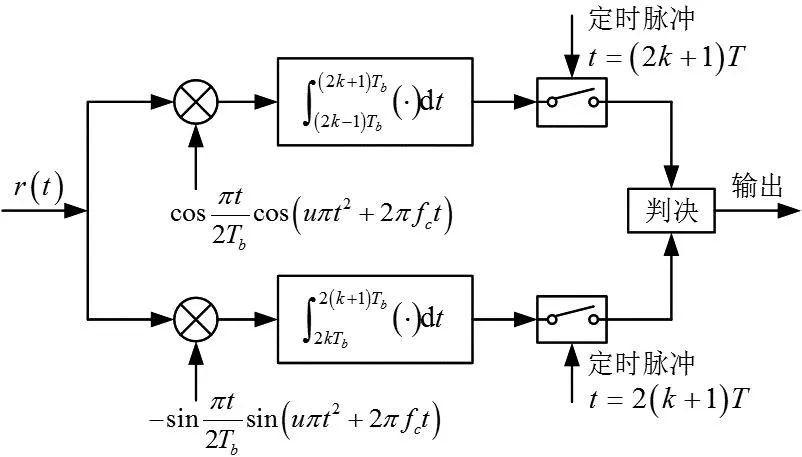
图8 MSK-LFM相关接收机原理图

取n=200,分别取fc=0.5、1、2、10 MHz,u=5、20MHz·μs-1,仿真次数为20万次,得到不同参数组合下的误码率曲线如图9。

图9 不同参数下误码率Pe随Eb/n0变化曲线

保持Eb/n0=8 dB不变,得到随fc、u变化曲线如图10～11。

图10 误码率Pe随fc变化曲线(u=5 MHz·μs-1)

图11 误码率Pe随u变化曲线(fc=0.5 MHz)

4 结 论

本文依据二进制数字信号最佳接收原理,对MSK-LFM码元相关性进行了理论计分析,并构建了高斯白噪声信道下MSK-LFM信号的正交调制解调模型,采用相关接收的方式仿真验证了MSK-LFM信号误码率同LFM载波初始频率、调频率及码元周期之间的关系。研究发现通过提高MSK-LFM信号的初始频率,可小幅改善通信误码率。当初始频率较大时远大于脉冲内码元调制速率时,此时继续增加初始频率或调频率,不会对误码率起到明显改善作用,但传、空号码元相关系数趋近于零,可认为其满足正交条件。而在发射功率一定的条件下,减少脉冲内码元调制个数,既可增加比特信噪比,又能降低码元相关系数。通过以上研究结论说明,在设计MSK-LFM一体化信号的参数时,应尽可能增加初始频率相对于码元调制速率的大小,选择调频率较大的LFM信号作为载波,当调频率和初始频率无法增大时,在满足通信速率要求的前提下应尽量降低码元调制速率。