基于曲梁理论的覆冰分裂导线舞动非线性动力分析

张孜航，韩艳 ，盛国刚，李凯

（长沙理工大学 土木工程学院，湖南 长沙 410114）

高压输电线常采取分裂导线来抑制电晕放电和减少线路电抗，以此显著提高线路的输电能力，例如双分裂、三分裂、四分裂甚至八分裂导线.舞动是导线覆冰形成非圆截面后在气动力作用下产生的一种低频、大振幅的自激振动，覆冰的分裂导线比单导线在风中更容易舞动［1-2］.为了全面描述覆冰导线的舞动行为，提出了涉及垂直、水平和扭转的三自由度模型［3］，结果表明在顺风方向上，导线的垂直、水平和扭转之间存在相互作用.

分裂导线的舞动可能会出现多阶模态的参与，而已有的模型并没有考虑到多阶模态的影响.为了更加精确地描述输电线舞动，提出了考虑多模态多自由度的分裂导线模型［4-6］.研究表明，三自由度下覆冰分裂导线的舞动考虑了“扭转效应”对分裂导线舞动特征的影响，将更符合真实状态下分裂导线的舞动行为，其结论更值得参考.另外，离散方法（直接离散法与间接离散法）对覆冰导线的频率、相位以及幅值都有一定程度的影响，且在扭转方向上，选择不同的离散方法所得的幅值差别较大；同时针对具体的覆冰导线进行舞动特征分析时，离散方法的不同可能会导致理论结果与实际工况存在差异，但是由于阶数过高时会使得计算过于复杂、计算效率降低，因此最多只考虑到了前六阶模态.

应用于覆冰导体舞动的有限元方法首先由Desai 等［7］提出，他使用一个三节点的索单元来模拟覆冰导体，采用时间积分算法对输电线舞动进行了分析，验证了该模型的优越性.李黎等［8］基于考虑扭转的索单元，建立了连续多档分裂导线舞动分析的有限元模型.通过对汉江大跨越工程覆冰导线的舞动分析验证了模型的可行性；并利用该模型研究了风速与初始攻角对舞动的影响.王黎明等［9］建立了考虑平动三自由度多档导线的运动模型，利用Fluent对一条500 kV 覆冰四分裂导线的舞动进行了研究.结果表明：在起舞风速与舞动最大幅值对应的风速之间，舞动幅值随风速的增加近似呈现线性增加的趋势.Zhou 等［10］利用ABAQUS 模拟输电线路舞动时，通过自定义的索单元对覆冰八分裂导线进行了节段模型的风洞试验，证明了数值方法的有效性.刘小会等［11］采用等参单元离散覆冰导线，用欧拉梁单元离散间隔棒，建立了覆冰分裂导线非线性有限元方程，通过算例验证了模型的正确性.向玲等［12］开展了不同档距四分裂线路的舞动特性和相地间隔棒防舞仿真分析，建立了不同档距四分裂线路和相地间隔棒的有限元模型，结果表明：不同档距四分裂线路的舞动特性不同，相地间隔棒的不同配置方案起到了明显的抑舞作用.Zhang 等［13］基于Desai 的索模型建立了分裂导线舞动的混合模型，并将该模型与有限元模型进行对比，结果表明该模型精确性高，可用于分析输电线舞动.这些覆冰分裂导线的有限元模型是基于经典的索结构理论，忽略了弯曲刚度，然而Luongo 等［14-15］认为弯曲梁理论可以更好地模拟轴向和扭转应变之间的耦合，并提出了一个考虑几何非线性与扭转的曲梁一致模型，同时认为在分析中不能忽略抗弯刚度对扭转刚度的影响.伍川等［16］基于ABAQUS 提出一种考虑偏心覆冰作用的导线数值模拟方法，并利用典型新月形覆冰四分裂导线算例验证了该方法的正确性.结果表明，考虑偏心覆冰作用后，覆冰四分裂导线的位移和扭转角幅值明显增大，振动形态更为复杂.因此，在研究覆冰导线舞动时，有必要考虑偏心覆冰作用的影响.

有限元方法能够有效地考虑横向与扭转之间的耦合作用.Zhu 等［17］提出了基于曲梁理论的六自由度单元模型，该单元考虑了弯曲刚度、平动振动和扭转振动的耦合.Yan 等［18］将此六自由度的曲梁模型用于分析输电线的舞动响应，分析表明该模型能有效地模拟输电线舞动的特性.Chen 等［19］针对受自激气动力影响的三自由度系统的模态频率、阻尼比和耦合运动，给出了复特征值问题的显式闭合解.然后将其应用于覆冰输电导线的三自由度舞动分析，并使用四分裂导线证明了方案的准确性.Foti 等［20］在更新的拉格朗日方法的背景下，提出了考虑索的几何非线性的共旋坐标系下的梁索单元公式.Xiong等［21］对曲梁模型进行了简化，并通过经典算例对模型进行了验证，结果表明输电线的弯曲模量对平移和扭转频率的影响较大，同时覆冰导线偏心率可略微降低导线的频率，但并没有分析气动力对结构频率的影响.

本文考虑覆冰产生的偏心惯性作用，假设间隔棒为刚体，提出了一种考虑弯曲刚度的曲梁覆冰分裂导线舞动分析混合模型，利用虚功原理建立了该混合模型的有限元方程并采用时间积分算法对非线性动力学方程进行了求解.同时进行了单元的无关性验证.通过有限元方法可考虑任意高阶模态对输电线舞动的影响，从而确定了模态的收敛性.分析了气动力对结构频率的影响.由于考虑了抗弯刚度、抗拉刚度与抗扭刚度的影响，该模型能更加准确地描述输电线的各自由度耦合舞动行为，有助于阐明分裂导线舞动的发生机理.

1 分裂导线混合模型

为了将单导线公式扩展到分裂导线，混合模型需做出如下假设［13］：

1）忽略纵向惯性力与阻尼力，只考虑分裂导线的整体运动；

2）导线垂跨比较小；

3）分裂导线绕参考曲线的旋转很小，且垫片是刚性的；

4）子导体的纵向运动彼此相同，且质心曲线的纵向运动相同；

5）在每个单元之间的节点上都有一个刚性垫片，垫片位于同一平面上，变形后没有翘曲.

Zhang等［13］基于Desai的索模型建立了分裂导线舞动的混合模型，但该模型并没有考虑弯曲刚度的影响.而Zhu 等［17］提出的六自由度曲梁模型对于应变-位移关系考虑得过于复杂，会导致有限元的计算量显著增加.因此本节采用虚功原理对考虑弯曲刚度的分裂导线混合模型进行计算，同时考虑偏心惯性作用，对分裂导线的舞动进行了模拟，该混合模型的应变-位移关系简单，可适用于任意数量的分裂导线，且更有利于后续舞动控制的实现.

为简单起见，图1（a）仅给出单跨两分裂导线示意图.杆塔与邻跨具有沿X方向和沿Z方向的刚度KST，绝缘体具有沿X方向的刚度和沿Z方向的刚度KIX与KIZ.其中X、Y、Z为模型的全局坐标.忽略邻跨惯性作用的影响并且认为支撑塔是刚性的，假设覆冰沿输电线分布完全相同.图1（b）给出了空间坐标系下的三节点覆冰分裂导线的混合模型曲梁单元，它们位于分裂导线的参考曲线上，其中，参考曲线的位置如图1（a）所示；U、V、W分别表示分裂导线在参考曲线的法向、副法向和切向的单元位移；s表示单元的弧坐标，单元随着局部坐标系x、y、z运动，每个节点有四个自由度（x、y、z方向的平动以及绕x方向的转动）.分裂导线混合模型单元内任一点的位移u见式（1），节点位移ue见式（2）.

图1 分裂导线模型Fig.1 Bundle conductor model

混合模型的基础是将分裂导线的行为等效为单导线的行为，这已被证明是有效的［13］.由于混合模型的曲梁单元模型在空间坐标系中的三个节点位于参考曲线上，由图1（c）可推导出参考曲线上的等效单元形心节点与第i个子导线之间的位移关系：

已知第i个子导线的节点位移，通过形函数可得到第i个子导线单元任一点的位移：

式中：ui为第i个子导线的单元位移；N为形函数矩阵［7］.

1.1 应变-位移关系

在局部坐标系下，忽略曲梁的剪切变形，考虑轴向、两个方向的弯曲以及扭转变形，第i个子导线的几何非线性应变-位移关系为［20］：

1.2 单元刚度矩阵

第i个子导线的单元刚度矩阵由单元线性刚度矩阵与单元非线性刚度矩阵组成：

式中：A为子导线的横截面面积；E、G、I1、I2分别为子导线的弹性模量、剪切模量和绕v、w的抗弯惯性矩；J为子导线的扭转惯性矩；T0为单元的初始拉力，线性与非线性应变矩阵为：

根据子导线与参考曲线之间的位移关系，得到分裂导线混合模型的单元刚度矩阵为：

式中：n为子导线的根数.

1.3 单元质量矩阵

第i个子导线的单元的一致质量矩阵为：

分裂导线混合模型的单元质量矩阵为：

1.4 单元结构阻尼矩阵

结构的阻尼对输电线舞动的影响至关重要，对于覆冰导线的舞动分析，通常通过假设瑞利阻尼并将其近似为对称结构阻尼矩阵［7，18］.第i个子导线的单元结构阻尼与单元质量和单元刚度有关，可写成如下形式：

式中：α和β分别为质量比例系数和刚度比例阻尼系数.若仅测量垂直、水平和扭转运动的第一模态阻尼比，则阻尼矩阵可近似为质量比例阻尼［7］.

分裂导线混合模型的单元阻尼矩阵为：

1.5 外荷载向量

第i个子导线的单元一致荷载矩阵可写为：

式中：Fy、Fz和Mθ分别为每单位导线长度的气动垂直力、侧向力和力矩.每单位导线长度的气动垂直力、侧向力力矩通常通过风洞测量在不同攻角下的准稳态升力Cy、阻力Cz和力矩系数Cθ来获得.

通过对覆冰导体进行准稳态风洞试验，确定其三分力系数.在对三分力系数进行拟合时，可采取如下的三次多项式：

式中：α为分裂导线混合模型的相对攻角［7，13］，α=0对应分裂导线混合模型在覆冰偏心作用下的静平衡位置.ai0表示静态风荷载，在时间积分过程中，可忽略该项对分裂导线舞动的影响.

上式计算的单元荷载由于存在积分，会导致在后续计算中计算量非常大，为了减少计算量，可写成单元集中荷载向量的形式［7］：

式中：Fyk和Fzk分别是单元第k个节点上的垂直与水平荷载；Mθk为相应节点上的力矩荷载，k=1，2，3.

分裂导线混合模型的单元荷载矩阵为：

1.6 分裂导线舞动的非线性动力学方程

根据虚功原理，以fei代表作用于第i个子导线的单元的全部节点荷载，对该单元可写出其虚功方程为：

式中：c为结构阻尼系数矩阵.

上式经过组装后最终形成如下的非线性动力学方程：

式中：M、C、KL和KNL分别为分裂导线混合模型的质量、阻尼、线性与非线性刚度矩阵；KQCL、KQCNL、KQL和KQNL分别为分裂导线混合模型的气动线性阻尼、气动非线性阻尼、气动线性刚度和气动非线性刚度矩阵；U为输电线的位移；分别为分裂导线混合模型位移对时间的一阶与二阶导数.气动力采用简化的式（18）进行计算.

式（24）在不考虑阻尼、非线性刚度与气动非线性刚度的情况下可写成如下的线性方程：

由式（25）可得到考虑气动线性刚度下的覆冰分裂导线的固有频率，当气动线性刚度（KQL）为零时，可得到覆冰分裂导线本身的固有频率.

2 舞动分析方法

可采用与单导线相同的方法分析分裂导线的舞动，即考虑空气动力和偏心重力载荷作用在所有子导线上，同时不考虑子导线间的遮挡效应，即假设各个子导线的气动力相等.通常，式（24）可以使用模态叠加法转换为前几个模态向量的模态空间［7，18］，然后通过二阶有限差分算法求解.前几个模态的选择可通过模态分析确定.应注意的是，为了减少计算量，在迭代过程中使用了静态平衡中的质量矩阵、阻尼矩阵和刚度矩阵.有关有限差分算法和时间积分的更多细节，请参考文献［7］.该算法可用于集成涉及非线性刚度、质量、阻尼、气动载荷和偏心重力载荷的动态平衡方程.

3 模型验证

在本节，通过一个经典算例［13］验证前面章节中描述的方法的准确性，该算例是基于Desai 的索模型分析分裂导线的舞动.二分裂、三分裂和四分裂导线横截面如图2 所示.子导线的弯曲刚度根据实体截面计算.具体子导线参数如表1 所示.Aice为覆冰导线的总横截面面积，μ为单位长度对应的质量，二分裂、三分裂和四分裂导线的动力学参数可参考文献［13］.需要注意的是在该算例中初始迎角和风速分别为40°和4 m∕s，时间步长为0.01 s.二分裂、三分裂和四分裂导线相应的跨中竖向静平衡位移分别为1.524 m、1.536 m 和1.572 m，满足小垂跨比的要求.有限元模型沿参考曲线有21个节点，其中节点1和节点21 分别为左边界和右边界，边界条件为简单支撑（V=θ=0，U≠0，W≠0），同时在分裂导线其他节点上配置了19 个虚拟的间隔棒且忽略间隔棒自身的质量与覆冰.

表1 子导线参数Tab.1 Conductor parameters

图2 分裂导线横截面Fig.2 Bundle conductor cross section

3.1 单元无关性检验

模型单元的划分对有限元结果具有极大影响，为了检验单元的无关性，讨论了不同的单元数量对二分裂、三分裂和四分裂覆冰导线前6 阶固有频率的影响，从而合理确定单元数目.第一阶模态、第二阶模态和第三阶模态分别表示侧向振动、竖向振动和扭转振动的一阶模态.另外，第四阶模态、第五阶模态和第六阶模态表示相应的二阶模态.

由图3可以看出，当将分裂导线划分为8个单元后，前六阶的频率并没有明显的变化.同时除了保证解具有一定的精度，还应考虑后续计算的时间成本，因此选取10个单元进行后续舞动时程分析的计算.

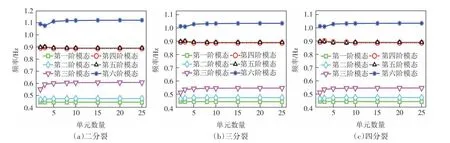
图3 单元无关性检验Fig.3 Element independence verification

3.2 模态收敛性

输电线的舞动可能会出现多模态的参与，因此，分析前十阶模态对二分裂、三分裂和四分裂覆冰导线舞动的响应，讨论分裂导线的模态收敛性.

由图4 可知：无论是二分裂、三分裂还是四分裂覆冰导线，前三阶、前五阶和前十阶模态的位移时程结果是一致的，而前二阶和前三阶的时程曲线均有明显差异，说明对于这些覆冰分裂导线的舞动起主要作用的是前三阶模态，因而在后续的舞动时程分析中可只取前三阶模态进行分析即可满足计算要求.

图4 不同阶模态计算结果Fig.4 Calculation results of different mode

3.3 舞动分析对比

本小节将分裂导线分为10 个单元，首先覆冰分裂导线本身的固有频率可通过式（25）得到，见表2.同时由式（24）计算覆冰分裂导线舞动时程，得到了对应的舞动稳态的极限环结果，从而验证模型的正确性，如图5所示.

表2 固有频率对比Tab.2 Comparison of natural frequencies Hz

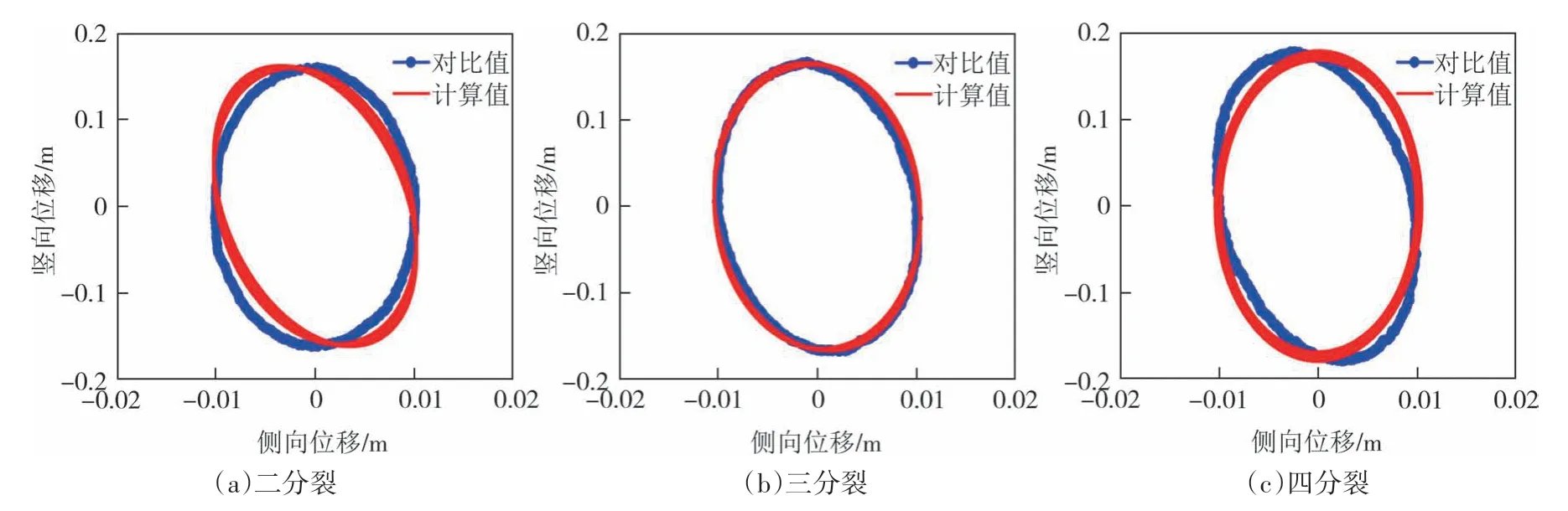
图5 跨中舞动位移对比Fig.5 Comparison of galloping displacement in mid-span

由表2 可知，分裂导线固有频率计算结果与Zhang 等［13］的基本一致，同时图5 表明混合模型计算结果与对比值基本一致，且各分裂导线的竖向极限环振幅在幅值上结果相差不大，它们比分裂导线的水平位移大得多，因此在实测中，分裂导线发生竖向运动是普遍的.同时验证了基于曲梁理论的分裂导线混合模型可用于计算覆冰分裂导线的舞动.

3.4 气动力对频率影响

前面的小节已验证了模型的正确性，本小节在式（18）的基础上通过改变风速使得气动力发生变化，然后通过式（25）计算得出气动力对频率的影响.

选取了一些常见的舞动风速.由图6（a）可知，二分裂导线在风速持续上升到25 m∕s 的过程中，第一阶扭转频率（第三阶模态）增大到了0.757 Hz，与无风条件下的频率相比增大了25.99%；第二阶扭转频率（第六阶模态）增大到了1.212 Hz，与无风条件下的频率相比增加14.25%.图6（b）所示三分裂导线的第一阶扭转频率增大到了0.675 Hz，增加17.88%；第二阶扭转频率增大到了1.112 Hz，增加6.87%.图6（c）所示四分裂导线的第一阶扭转频率增大到了0.723 Hz，增加21.03%；第二阶扭转频率增大到了1.174 Hz，增加8.38%.无论是二分裂、三分裂还是四分裂导线，它们的第一阶与第二阶的侧向与竖向频率（第一阶模态、第四阶模态、第二阶模态与第五阶模态）基本无变化.结果表明，气动力对侧向与横向频率基本无影响，而对扭转频率影响较大且对第一阶扭转频率的影响更为明显.

图6 气动力对频率的影响Fig.6 Influence of aerodynamic force on frequency

4 结论

基于空间曲梁理论的应变-位移关系，采用虚功原理建立了考虑气动刚度与气动阻尼的覆冰分裂导线舞动非线性动力学混合模型，利用振型叠加结合时间积分算法对方程进行求解.在数据仿真中，进行了单元和时间无关性检验和模态收敛性的计算，最后分析了气动力对不同分裂导线舞动前六阶频率的影响，可以得出以下结论：

1）通过与以往文献的比较，验证了目前的研究结果.此外，由于单元的简单性和有效性，本混合模型对于覆冰分裂导线的动态控制具有更好的适用性.

2）根据单元与时间无关性检验结果，在本例中单元的数量不应少于8 个.此外，通过对覆冰分裂导线进行非线性动力分析可得到在舞动计算中选择前三阶模态是合理的.对于不同的模型，为了满足计算精度的要求，单元数量和模态截断数量可能会发生变化.这些结果为准确建立覆冰导线的非线性动力学模型提供了计算依据.

3）当风速增加到25 m∕s时，二分裂、三分裂和四分裂导线一阶扭转频率分别增加25.99%、17.88%和21.03%，二阶扭转频率分别增加14.25%、6.87%和8.38%.而一阶和二阶横向和垂直频率基本保持不变，说明气动力对扭转频率影响较大且对第一阶扭转频率的影响更为明显.计算结果更准确地反映了覆冰分裂导线的动态特性，同时为后续动态控制的实施提供更为准确的依据.