双三相永磁同步电机改进型模型预测电流控制

2024-03-25高锋阳徐昊杨凯文史志龙高智山强雅昕

湖南大学学报（自然科学版） 2024年2期

高锋阳，徐昊，杨凯文，史志龙，高智山，强雅昕

（兰州交通大学自动化与电气工程学院，甘肃兰州 730070）

双三相永磁同步电机具有功率密度高、可靠性高、转矩脉动小以及可以实现低压大功率输出等优点，在机车牵引、电动汽车、船舶推进等领域已经得到广泛应用［1-2］.相较于其他多相电机而言，双三相电机可以利用传统三相电机系统较为成熟的控制技术，因而更具优势［3］.

双三相电机存在谐波平面，易产生较大谐波电流，同时多相逆变器可以输出更多的电压矢量，如何控制谐波平面以及快速选择最优电压矢量是双三相电机系统亟待解决的问题.矢量控制可以控制谐波平面，但需要进行更多的PI 调节器参数整定较为复杂［4］；直接转矩控制可根据开关表快速选择电压矢量，但无法抑制谐波电流，且选择的未必是最优电压矢量，从而影响电机的稳态性能.模型预测控制（Model Predictive Control，MPC）因其可实现多目标控制以及依据价值函数寻优的特点，为解决上述问题供了新思路.传统模型预测控制（Traditional Model Predictive Current Control，TMPCC）在价值函数中增加谐波电流项权重系数［5］，实现谐波电流抑制，但权重系数的选择缺乏理论基础，若增加算法对权重系数进行寻优势必会增加控制器计算负担［6-7］.文献［8-9］利用虚拟电压矢量抑制谐波电流，避免了权重系数的选择，然而多个虚拟电压矢量的遍历寻优仍会产生不小计算负担.宋文祥等［10］将转矩控制和模型预测结合，使寻优次数减少为4次.

然而，上述研究均未考虑逆变器驱动电机产生的共模电压问题.共模电压会使得电机系统电磁干扰加剧，导致控制电路以及电气设备产生误动作［11-12］.除此之外，共模电压产生的轴电压和轴电流会损坏电机绝缘、腐蚀电机轴承，影响电机使用寿命［13-14］，因此，需要抑制驱动系统产生的共模电压.现有研究减少共模电压主要通过两种方式，其一是使用无源或有源滤波器［15-16］，但额外的硬件电路会增加系统的成本与体积；另一种方式则是改变控制策略.Un 等［17］和Lai 等［18］通过脉宽调制的方法抑制共模电压，但Un 等的研究会影响电压调制比［17］，Lai等的研究会使开关频率增加［18］.就MPC而言，可以在代价函数中增加共模电压权重系数［19］（Reduced Common Mode Voltage，RCMV-1），此方法需对电流谐波和共模电压权重系数配合调整，使得权重系数的选择更加复杂.因此，通常采取弃用产生较大共模电压矢量的方法抑制共模电压.徐质闲等［20］利用三电平逆变器的零共模电压矢量控制电机，抑制了共模电压，却需另外引入中点电位平衡权重系数.对于两电平逆变器抑制共模电压，应避免零矢量的选取［21-22］.Yu 等［21］和孙全增等［22］分别针对五相和双三相电机，利用非零矢量合成虚拟电压矢量控制电机，简化代价函数的同时减小了共模电压（RCMV-2），但两者均采用对固定幅值电压矢量集寻优的方法，使得电机稳态控制精度不高、转矩脉动增大，同时还需进行多次寻优计算.此外，为提升电机稳态控制精度，还合成了虚拟零矢量加入控制集，使得开关频率升高［21-22］.

综上，本文针对双三相永磁同步电机，提出一种改进型模型预测控制方法.首先，改进六相两电平逆变器，抑制零矢量共模电压，选取小共模电压矢量构造虚拟电压矢量控制集，兼顾低共模电压和谐波电流；然后，用虚拟矢量，结合零矢量控制电机，提升电机稳态性能.最后，对TMPCC、RCMV-1、RCMV-2 和所提控制方法进行仿真对比分析.结果表明，所提控制方法可以抑制共模电压改善电机的稳态性能，减小开关频率和计算量.

1 双三相永磁同步电机系统

1.1 电机驱动系统及数学模型

双三相永磁同步电机定子绕组由两套Y 型连接方式的三相绕组构成，两套绕组空间上电角度相差30°，且中性点相互隔离.一组六相两电平逆变器为电机供电.电机驱动系统原理如图1所示.

图1 双三相永磁同步电机驱动系统Fig.1 Dual three-phase permanent magnet synchronous motor drive system

与三相系统类似，双三相永磁同步电机可通过空间矢量解耦变换，将六维空间映射到α-β、x-y、o1-o2三个相互正交的子平面，α-β子平面包含基波和12k±1（k=1，2，3…）次谐波，该平面参与机电能量转换；x-y谐波子平面包含6k±1（k=1，3，5…）次谐波；o1-o2零序子平面包含6k±3（k=1，3，5…）次谐波，由于定子绕组中性点采用相互隔离星形连接方式，故不考虑该子平面.通过坐标变换可得双三相永磁同步电机在dq轴和xy轴数学模型为

式中，ud、uq、id、iq分别为d 轴和q 轴上的电压和电流；ux、uy、ix、iy分别为x轴和y轴上的电压和电流；Rs为定子电阻；Ld和Lq是d 轴和q 轴上的电感；ω为电角速度；ψf为永磁体磁链；Lls为定子漏感.

1.2 空间电压矢量和共模电压

逆变器的全部开关状态，可表示为与之对应的电压矢量，具体为

式中，a=ej30°；PA、PB、PC、PU、PV、PW取值为0 或1，分别表示对应相的开关状态；uαβ和uxy分别为α-β、x-y平面电压矢量；Udc为逆变器的直流电压幅值.

六相桥臂共存在26种开关状态，故有64 个电压矢量与之对应.电压矢量由六相桥臂对应的开关状态转换为十进制数编号表示，例如：当A～W 相开关状态为（100010）时，100 表示ABC 三相开关状态对应十进制数4，010 表示UVW 三相开关状态对应十进制数2，故对应电压矢量为u42.所有电压矢量，空间分布如图2 所示，除零矢量外依据幅值由大到小分组表示为L1、L2、L3、L4，如表1所示.

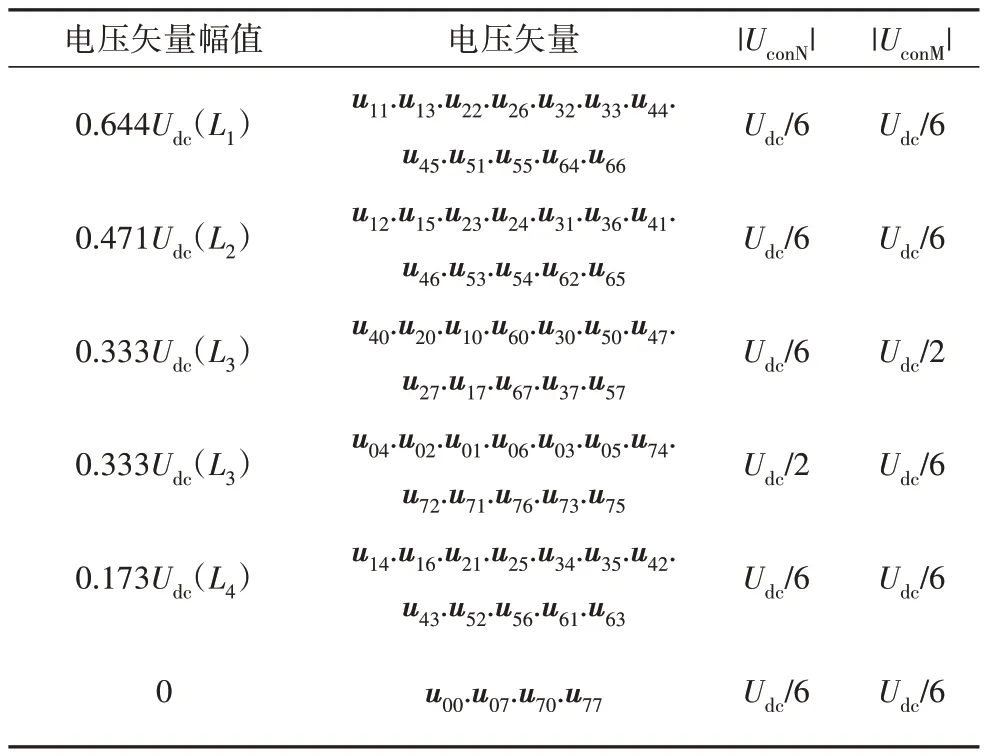
表1 电压矢量分组Tab.1 Different groups of voltage vector

图2 六相逆变器电压矢量分布Fig.2 Six phase inverter voltage vector distribution

对于中性点相互隔离的双三相永磁同步电机，共模电压为两个绕组中性点分别和直流侧母线中点之间的电压，分别用UconN、UconM表示，具体计算式为

式中，UconN、UconM分别为ABC、UVW 两套绕组的共模电压；UAO、UBO、UCO、UUO、UVO、UWO为逆变器输出的六相电压.

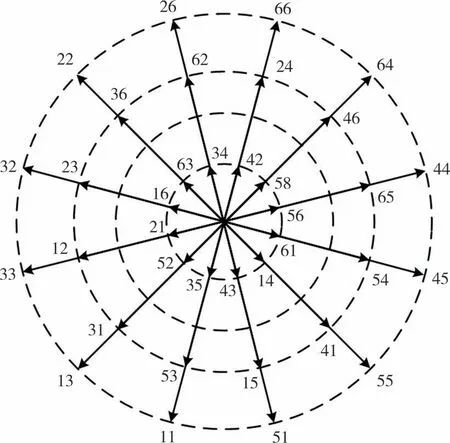
图3 小共模电压矢量分布Fig.3 Small common-mode voltage vector distribution

2 低共模电压模型预测电流控制

2.1 传统低共模电压模型预测电流控制

利用前向欧拉法对式（1）进行离散化处理，可得双三相永磁同步电机电流预测模型为

式中，id(k+1)、iq(k+1)、ix(k+1)、iy(k+1)为k+1时刻dq轴和xy轴预测电流值；Ts为采样周期.

根据k时刻采样的电流值，预测64 个电压矢量作用下在k+1 时刻的电流值，最后依据价值函数寻优，对应选择价值函数最小的电压矢量在k+1 时刻作用于电机.为抑制谐波电流、减小共模电压，在代价函数中增加谐波电流以及共模电压相关项权重系数，具体为

由此可知，传统低共模电压模型预测电流控制（RCMV-1）需要对全部64 个电压矢量遍历寻优，计算量较大.同时，权重系数一般根据经验选取，缺乏理论依据，为兼顾电流质量和低共模电压，两个权重系数的配合整定更加困难，若增加额外算法对权重系数进行寻优无疑会进一步增大计算负担.

2.2 虚拟电压矢量构造方法

为消除权重系数、减小谐波电流和共模电压，文献［22］提出了一种基于虚拟电压矢量合成的方法（RCMV-2）.首先，在一个控制周期内，选择两个小共模电压矢量作用相应的时间以构造虚拟电压矢量，令其在x-y谐波平面等效幅值为0，以此来达到抑制谐波电流和减小共模电压的目的，依据虚拟电压矢量的α-β平面幅值分为VVL、VVM、VVS三组；其次，为减小电机转矩脉动，提升电机控制裕度，另合成了一组虚拟零矢量VVZ；最后，根据价值函数对四组幅值不同的虚拟电压矢量进行寻优.控制方法如图4所示.

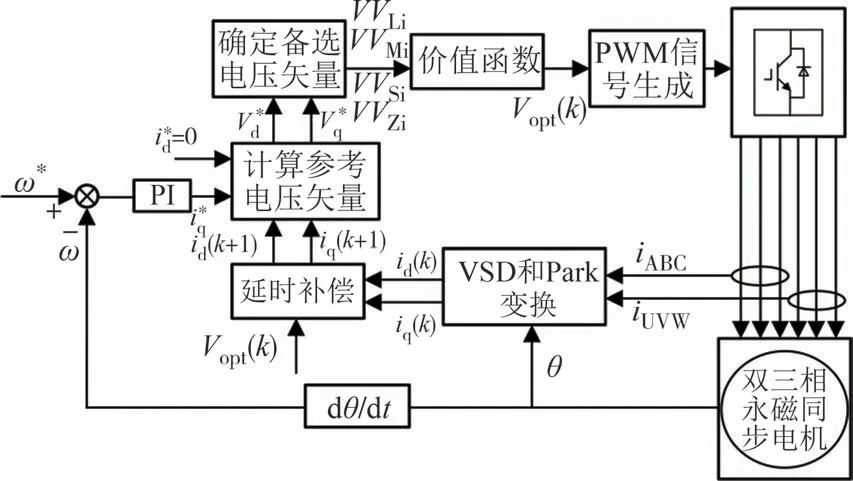
图4 文献［22］提出的共模电压抑制方法Fig.4 Common-mode voltage suppression method proposed in［22］

基于虚拟电压矢量合成的方法可以消除权重系数，但固定幅值的虚拟电压矢量，会影响电机的控制精度，并且仍需进行4 次寻优计算；除此之外，虚拟零矢量会明显增加开关频率，增加系统损耗.

3 改进型控制策略

3.1 改进六相逆变器

由前文分析可知，为减小共模电压，零矢量属于大共模电压矢量，因此会被弃用，但弃用零矢量会使得电机稳态性能下降，然而文献［22］合成虚拟零电压矢量的方法，会增加开关频率.因此，对传统六相两电平电压源逆变器进行改进，在直流电源和逆变器之间额外增加两个开关管，并对其并联反向击穿电压为Udc/3的稳压管，如图5所示.

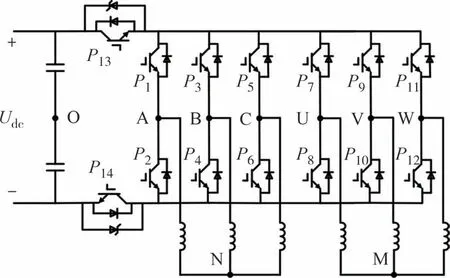
图5 改进型六相电压源逆变器Fig.5 Improved six-phase voltage source inverter

P13、P14的开关函数为

式中，P1～P14为相应开关管，状态取值0或1.

以作用电压矢量u77为例，开关P13关断、P14打开，此时开关P13并联的稳压管被击穿，其承担Udc/3的电压，逆变器输出六相电压为Udc/6，共模电压UconN和UconM为Udc/6，如图6 所示，采用改进逆变器结构减小零矢量u00和u77的共模电压幅值.

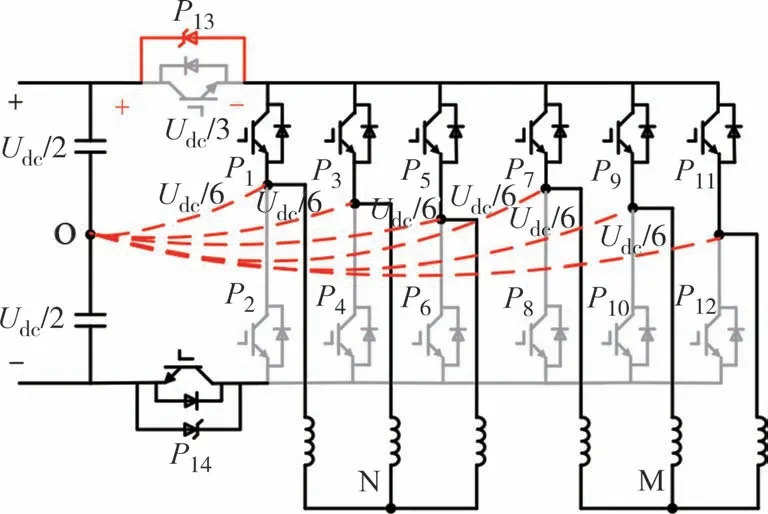
图6 电压矢量u77作用时的共模电压Fig.6 The common-mode voltage of u77 is applied

3.2 构造虚拟电压矢量

虚拟电压矢量由若干基本电压矢量设置作用时间合成.为兼顾低共模电压和谐波电流，选取图3 所示36 个小共模电压矢量中的若干个构造虚拟电压矢量，并设置它们的作用时间，使其在一个控制周期内合成的等效矢量幅值在x-y平面为0.图7 给出了由u44和u65、u44和u21、u65和u56以及采用u55、u45、u44、u64四个相邻矢量的四种虚拟电压矢量的合成方法，以u44和u65合成为例，根据伏秒平衡原理，需满足

|V1|αβ和|V1|xy为合成虚拟电压矢量在α-β平面和x-y平面幅值，令|V1|xy=0，得

同理可得，图7 中（b）（c）（d）三种方式合成的虚拟电压矢量在α-β平面幅值分别为0.472Udc、0.345Udc和0.577Udc.为提高电压利用率，选择如图7（a）所示方法合成虚拟电压矢量，合成的12 个虚拟电压矢量如图8所示.

图7 虚拟电压矢量合成方式
Fig.7 Virtual voltage vector synthesis methods

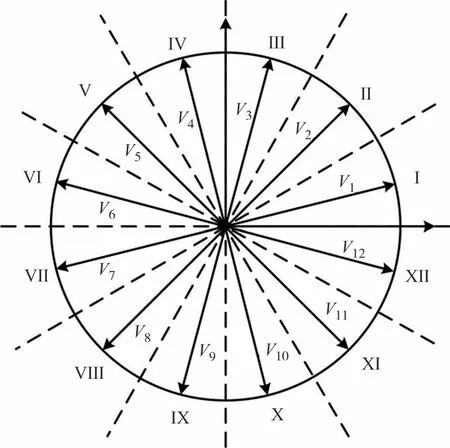
图8 构造的虚拟电压矢量分布Fig.8 Constructed virtual voltage vectors distribution

3.3 电压矢量寻优及占空比计算

备选电压矢量由12 个虚拟电压矢量以及两个零矢量组成，此时价值函数可以简化为

由式（9）可知，新的价值函数避免了权重因子的选择，但仍需进行13 次寻优计算，为进一步简化寻优计算，由参考电压所处位置选择最优电压矢量.首先，根据式（4）以及电流无差拍原理，可得参考电压矢量在d轴和q轴的分量为

根据式（12）获得参考电压矢量位置，由其所处扇区选择最优电压矢量，例如当参考电压矢量位于扇区Ⅰ时最优电压矢量为V1，仅进行一次参考电压矢量的计算，减小了计算量.

若每个控制周期仅采用单个虚拟电压矢量控制，虽然可以抑制谐波电流，但电机会产生较大转矩脉动，为此引入占空比控制，采用虚拟电压矢量和零矢量结合的方式，提升电机的控制精度，改善电机稳态性能.

由式（4）可得电流变化率为

式中，Vdi、Vqi为虚拟矢量在d、q轴的分量.

设虚拟电压矢量作用时间占空比为d，则零矢量为1-d，k+1时刻预测电流值为

式中，Sdi、Sqi、Sd0、Sq0分别为虚拟电压矢量和零矢量作用时d、q轴电流变化率.

此时，应选择最优占空比d，使得预测值与参考值误差最小，即式（9）取得最小值，故有

联立式（9）、式（13）和式（15）可得

3.4 PWM波形中心化处理

当作用的虚拟电压矢量为V1时，其产生的PWM原始波形如图9（a）所示，如果不对其进行中心化处理会存在两点弊端.其一，不对称的波形会增加定子电流谐波含量，并且不利于硬件的实施［23］；另外，这种不固定的开关动作方式，可能存在两相开关状态同时变化，例如，两个周期均作用虚拟电压矢量V1时，会存在由u65向u00切换的情况，即两相开关状态同时变化，可能在死区产生等效零矢量，导致死区的共模电压尖峰［24］.因此，在保证每相桥臂导通时间不变的情况下对脉冲序列进行中心化处理，如图9（b）所示，由图可知，每次只允许一相开关状态动作，在保证PWM 波形对称的同时可以避免死区时间可能产生的共模电压峰值.

图9 PWM信号及共模电压Fig.9 PWM signal and common-mode voltage

3.5 改进型控制方法

本文提出的改进型模型预测控制系统框图如图10所示，步骤如下：

图10 改进型模型预测控制系统框图Fig.10 System diagram of an improved model predictive current control

1）采样获得当前周期的电流、转子位置、转速等信息.

2）通过转速外环PI 调节器计算q 轴参考电流值，d轴参考电流值设为0.

3）利用式（10）～式（12）计算参考电压矢量，根据参考电压矢量所处扇区选择最优虚拟电压矢量.

4）根据所选最优虚拟电压矢量，利用式（14）、式（16）和式（17）计算虚拟电压矢量占空比.

5）利用计算的占空比，对输出PWM 信号进行中心化处理后作用于逆变器.

4 仿真验证

当2.1 节介绍的方法共模电压权重系数取0 时，即为TMPCC，当共模电压权重系数取10 时为RCMV-1，两者的谐波权重系数均设置为0.1，2.2 节所用方法为RCMV-2，通过Matlab/Simulink将上述方法和所提控制方法进行仿真对比分析，电机驱动系统参数如表2所示.

表2 双三相永磁同步电机参数Tab.2 Dual three-phase PMSM parameters

4.1 稳态性能对比

为了对比四种控制方法的稳态性能，首先在低速稳态对四种控制方法进行了仿真对比.图11 为采样频率20 kHz、转速400 r/min、负载20 N·m 工况条件下四种控制方法的稳态波形图.

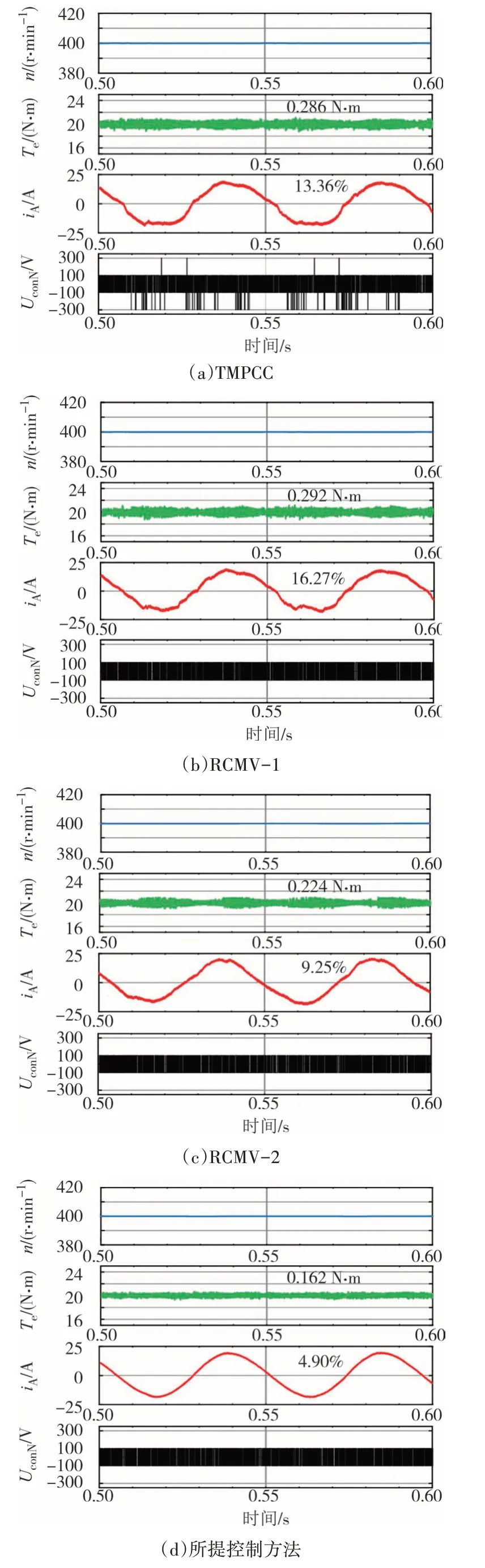
图11 低速稳态仿真结果Fig.11 Simulation results of steady-state at low speed

定义转矩脉动计算公式为

由图11可以看出，TMPCC 转矩脉动和电流THD（总谐波失真）值较大，分别为0.286N · m 和13.36%，并且会产生幅值为±Udc/2 的共模电压；RCMV-1虽然将共模电压的幅值减小为±Udc/6，但却使得电机的转矩脉动以及THD 增加；RCMV-2 将共模电压幅值降低为±Udc/6，同时将电流THD 减小到9.25%，但转矩脉动较大；所提控制方法降低共模电压的同时转矩脉动最小，并且电流THD为4.90%.

为了进一步对比四种控制方法的稳态性能，在高速稳态对四种控制方法进行了仿真对比.图12 为电机在转速1 000 r/min，负载转矩为20 N·m 工况条件下四种控制方法的仿真结果.从图12 可以看出，TMPCC 的转矩脉动和电流THD 较大，分别为0.288 N·m 和6.96%，并且会产生幅值为±Udc/2 的共模电压；RCMV-1 可以将共模电压的幅值减小为±Udc/6，但转矩脉动和电流THD 最大；RCMV-2 将共模电压幅值降低为±Udc/6，同时将电流THD 减小到4.82%，但会产生较大的转矩脉动；所提控制方法降低共模电压的同时减小了转矩脉动，并且电流THD为2.53%.

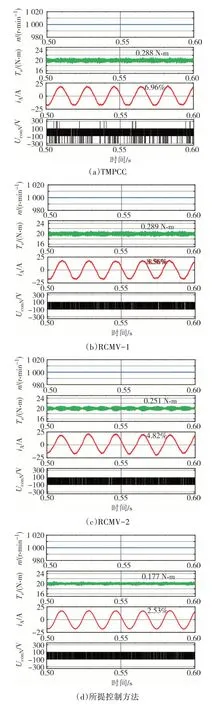
图12 高速稳态仿真结果Fig.12 Simulation results of steady-state at high speed

由图11 和12 可知，RCMV-1 通过设置共模电压权重系数，抑制了共模电压，却导致电机的转矩脉动和电流THD 增加，说明谐波电流和共模电压权重系数会相互影响，需配合整定；RCMV-2 通过构造虚拟电压矢量可以抑制电流谐波，但固定幅值的电压矢量仍会产生较大转矩脉动；所提控制方法在抑制共模电压的同时，降低了电机定子电流的THD和转矩脉动.

4.2 动态性能对比

为了验证所提控制方法的动态性能，对四种控制方法进行了动态仿真对比.图13 为负载转矩由初始的20 N·m，在0.3 s 时突增至30 N·m，0.6 s 时突减至25 N·m 工况条件下的四种控制方法仿真对比.由图13 可知，在相同转速情况下，当突加负载时，TMPCC、RCMV-1、RCMV-2 和所提控制方法对应的调节时间分别为144 ms、145 ms、140 ms、135 ms，当突减负载时四种控制方法所对应的调节时间分别为118 ms、113 ms、122 ms、119 ms.由此可知，四种控制方法在负载变动时动态响应没有明显差异，电机转速和转矩都能快速准确跟踪设定值，但所提控制方法转矩脉动更小.

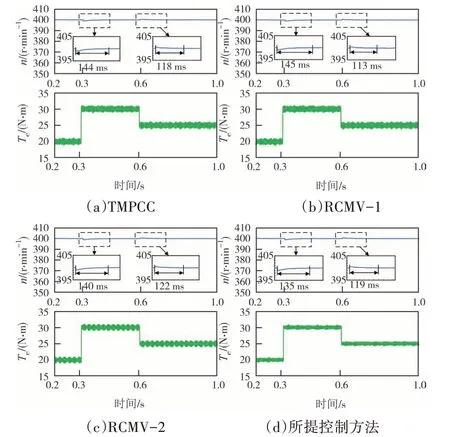
图13 动态仿真结果Fig.13 Results of dynamic simulation

4.3 开关频率对比

图14 为电机转速200 r/min、负载转矩20 N · m工况下分别采用四种控制方法时，A 相桥臂一逆变器在一段时间内的开关状态，0 代表关闭，1 代表打开，上升和下降沿代表开关状态的变化.由图14 可知，TMPCC 和RCMV-1 控制方法开关频率基本相同且较小；RCMV-2 方法开关频率最高；所提控制方法开关频率高于TMPCC 和RCMV-1 控制方法，但明显低于RCMV-2控制方法.统计（0.5～0.6）s内四种控制方法的开关频率，分别为13.9 kHz、13.8 kHz、25.1 kHz、20.0 kHz，由于RCMV-2 和所提控制方法均采用了虚拟电压矢量，一个周期含两到三个基本矢量，故开关频率较高.

图14 开关状态对比Fig.14 Comparison of switching state

图15 为RCMV-2 和所提控制方法在不同转速和负载转矩工况下开关频率对比.由图可知，在不同工况下所提控制方法开关频率固定且均低于RCMV-2，这是由于RCMV-2 的虚拟零矢量由三个电压矢量合成，故开关频率会升高，特别当低速轻载时更甚，因为此时虚拟零矢量作用次数增多.

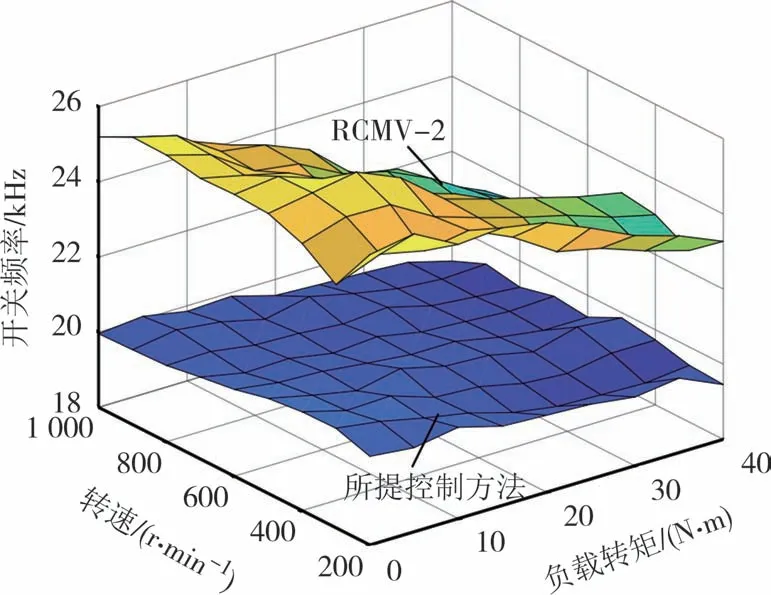
图15 不同工况下开关频率对比Fig.15 Comparison of switching frequency in different working conditions

4.4 鲁棒性验证

由于电机正常运行时，电机参数可能会发生变化，为验证所提控制方法的鲁棒性，给定电机负载20 N·m、转速1 000 r/min，分别使电机电阻增加20%、电感不变，电阻减小20%、电感不变，电阻不变、电感增加20%，电阻不变、电感减小20%.四种情况下的仿真结果如图16所示.

图16 参数失配仿真结果Fig.16 Simulation results with mismatched parameters

与图12（d）参数不变的情况进行对比，如表3 所示.可以发现，当参数在一定范围内变化时，采用所提控制方法对电机转矩脉动和电流质量不会产生较大影响.

4.5 计算量对比

最后，对三种抑制共模电压控制方法的计算量进行了对比，并统计寻优代码执行一次所需时间，如表4 所示.由于TMPCC 和RCMV-1 备选电压矢量为所有电压矢量，因此要进行64次寻优计算；RCMV-2虽然备选电压矢量减少，但仍需要进行4 次寻优计算，而所提控制方法只需进行1 次参考电压矢量的计算，可以减少计算时间.