基于GARCH类模型对美国股市波动性的对比分析

李姜悦 沈慈慈 王伟杰

(淮北理工学院 安徽淮北 235000)

随着全球金融市场的日益相互联系和国际金融风险的增加，金融市场的波动性成为重要的研究领域。美国作为全球最大的经济体，其金融市场的波动性对全球经济有着巨大的影响。

为了更好地刻画时间序列的波动率，Bollerslev(1986)[1]对自回归条件异方差(Autoregressive Conditional Heterosc edasticity，ARCH)模型进行了拓展，建立了广义自回归条件异方差模型(Generalized Autoregressive Conditional Heteroscedasticity Model，GARCH模型)。因为波动性是市场风险的度量，可以反映市场的不确定性，反映投资者对市场的情绪和态度，因此国外学者借助GARCH类模型对股市波动性的研究层出不穷；Edbert和Sigit(2018)[2]基于GARCH类模型对东盟五国的油价波动和股票收益进行了实证分析；Takwi(2023)[3]通过GARCH模型对喀麦隆股市的波动率进行实证分析，表明相比ARCH模型，GARCH模型能够很好地衡量喀麦隆股市的波动率；Maria等(2023)[4]利用英国上市公司高管内幕交易的月度数据分析了内幕交易总量( AIT )与股市波动之间的关系，发现较高的AIT会导致股市波动率的短期上升。

国内学者对中国股市波动性的研究也取得了一些研究成果；王孜(2022)[5]通过构建GARCH模型实证研究发现，融资业务会平抑中国股票市场的波动，融券业务则会加剧股票市场的波动；苏晴(2022)[6]通过比较分析认为，GARCH-t模型能较好地刻画沪深300指数收益率的变动趋势；周健等(2022)[7]基于ARCH类模型实证分析了新三板市场股票收益率的波动性，研究得出收益率波动频繁且幅度较大，存在明显的非对称效应，且高收益与高风险呈正相关关系。

本文选取2010年6月1日—2020年10月31日美国股市的Nasdaq指数和Russel2000指数的日交易数据作为样本，同时运用GARCH(1，1)模型和APARCH(1，1)模型探究两种股指的波动性特征，从而对美国股市进行对比分析，并对波动率进行预测，可为投资者更好地投资提供参考。

1 研究基础

GARCH(1，1)模型和APARCH(1，1)模型均是探索时间序列波动性的有效模型。本文对美国股市的股指采用两种模型建模，并进行对比分析，GARCH(1，1)模型表达式为：

均值方程：

方差方程：

APARCH(1，1)模型表达式为：

均值方程：

方差方程：

2 实证分析

2.1 数据选取与处理

本文从雅虎财经网分别选取2010年6月1日—2020年10月31日美国股市的纳斯达克指数(Nasdaq)和罗素2000指数(Russel2000)2623个交易日的收盘价数据，因为资产收益率序列比价格序列易处理且更具研究意义，因此对收盘价作日对数收益率处理：

式(5)中：Rt是每个指数的日收益率，Pt是每个指数在t交易日的日收盘价，Pt-1是上一交易日的日收盘价，对每个指数的2623个收盘价计算，可以得到2622个对数收益率。

2.2 数据描述性统计信息

对Nasdaq和Russel2000两种指数的日对数收益率进行统计学分析，结果如表1所示。

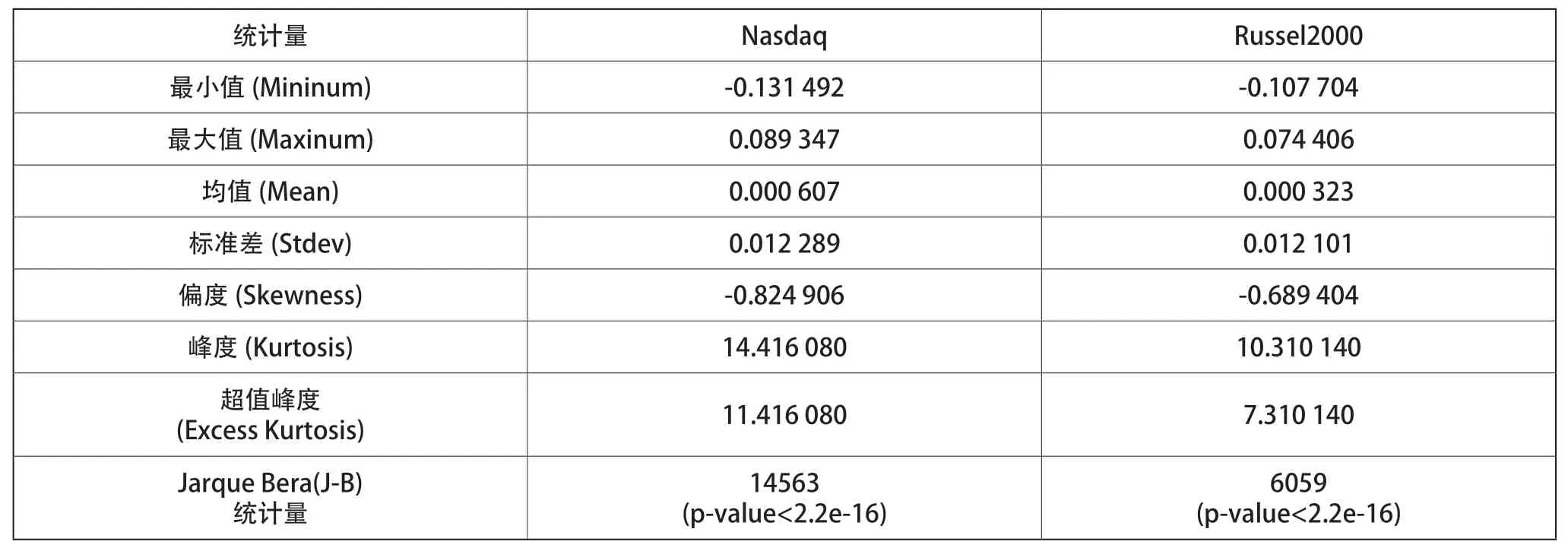
表1 Nasdaq、VIX的日对数收益率的描述性统计量信息

由表1可知：第一，两种指数的日对数收益率最小值都为负值，最大值都为正值，均值都接近零值且大于零，表明两种指数的波动方向相同，且美国股市长期处于波动上升期，认定为“牛市阶段”，尤其是两大指数的最小值与最大值相差不大，所以市场调节灵活度较高；第二，两种指数的标准差都为正值且都接近零值，Russel2000相对Nasdaq的标准差稍小一些，表明Russel2000指数日对数收益率的波动性低于Nasdaq的波动性，Russel2000的风险相对较低，更适合投资；第三，Nasdaq和Russel2000的偏度值均为负值，即其日收益率序列存在左偏现象，不符合正态分布的对称性，且对两种指数的偏度取绝对值发现，Nasdaq的偏度值较大，Russel2000的偏度值较小，Nasdaq的左偏更严重；第四，两种指数的峰度最小值为10.310140，比正态分布的峰度值3大得多，表明两种指数的日对数收益率序列都存在尖峰肥尾现象，不满足正态分布；第五，两种指数日对数收益率J-B统计量检验下的P值都小于2.2e-16，在0.1%的显著水平上都显著，进一步表明两种指数日对数收益率序列都不满足正态分布。

2.3 分位数-分位数(Q-Q)图

在运用GARCH(1，1)模型对这两种指数的日对数收益率的波动性分析建模之前，需要对数据进行正态性检验。本文采用分位数-分位数(Q-Q)图检验所选取的两种指数是否具有非正态性。

如图1所示，两种指数的Q-Q图都呈黑色曲线，正态分布的Q-Q图是一条直线，两种指数的日收益率序列都不与图中的直线重合，所以两种指数日对数收益率都具有非正态性。

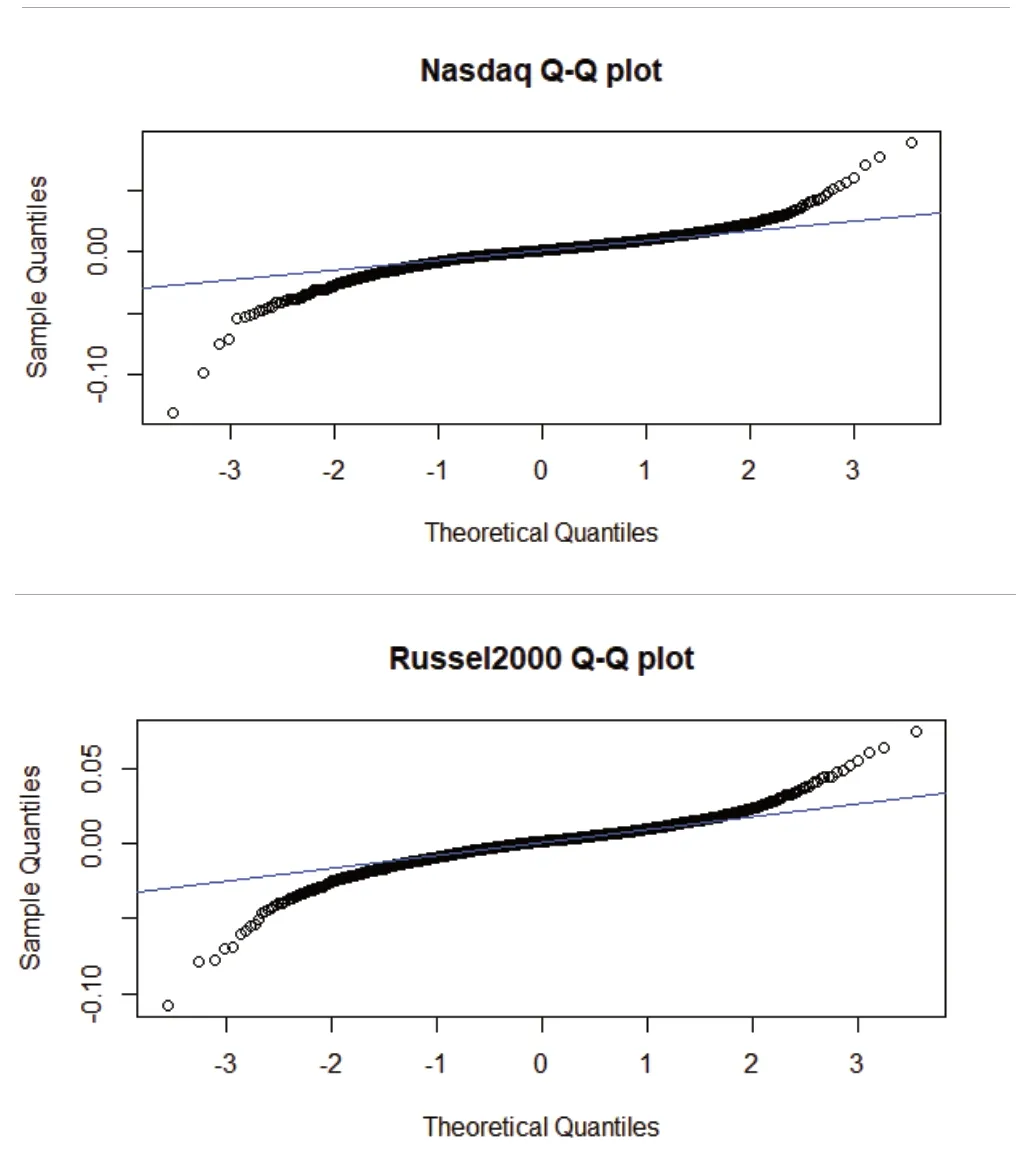
图1 Nasdaq和Russel2000日对数收益率Q-Q图

2.4 日收益率曲线时序图

考虑到日收益率序列波动幅度小，序列较平稳，因此进一步利用日对数收益率时序图观察波动聚类现象的存在及分布的非正太性。

由图2可知：第一，两种指数的日对数收益率在平均值零的上下范围内波动，且低波动周期持续时间长。Nasdaq在2011年和2017年上半年呈高波动周期，并在2017年上半年达到最大幅度波动。Russel2000在2011年和2020年呈高波动周期，并在2020年上半年达到最大幅度波动；第二，2011年、2017年上半年和2020年上半年高波动周期的持续时间都较短，这种低波动之后高波动的随机过程表明美国股市存在波动聚类现象和非正态性，且两种指数日收益率序列的方差是时变的；第三，低波动周期表明指数日收益率在此阶段的风险较低，高波动周期则表明风险较高，两种指数的日对数收益率从2011—2017年是低波动周期且持续时间相对较长，表明美国股市在这段时期存在低收益和低风险现象，而在2011年、2017年上半年和2020年上半年存在高收益和高风险现象。

图2 Nasdaq和Russel2000日对数收益率曲线时序图

2.5 平稳性检验

为了使行时间序列分析具有意义，需对两种指数的日对数收益率序列的平稳性进行检验。平稳性检验一般有6种方法，现对两种指数分别使用ADF(Augmented Dickey-Fuller)检验和P-P(Phillips-Perron Unit Root test)检验两种方法，结果如表2所示。

表2 两种指数的日对数收益率平稳性检验

在表2中，两种指数日对数收益率的ADF检验和P-P检验值是在滞后阶数和截断滞后参数均是13的条件下得出的，两种检验方法的p值都小于0.01，表明两种指数日对数收益率不存在单位根，时间序列是平稳的。

2.6 相关性检验

在对日对数收益率建模前，还要检验收益率的自相关性。ACF(Autocorrelation Function)图和PACF(Partial Autocorrelation Function)图是用来检验收益率变量之间相关程度的两种方法。一般来说，PACF图更能反映变量相关性的真实性，检验结果如图3、图4所示。

图3 Nasdaq和Russel2000日对数收益率序列ACF图

图4 Nasdaq和Russel2000日对数收益率序列PACF图

由图3可以看出，ACF图和PACF图在滞后阶数为0～30大部分函数值都在置信区间内，即图中虚线区域上下跳跃，所以收益率序列自相关性很低，因此在条件期望模型中不需要引入自相关性部分，满足GARCH模型中的均值方程。

2.7 ARCH效应检验

在用GARCH模型拟合收益率之前，需要检验收益率数据中是否存在自回归条件异方差，即ARCH效应。表3是采用拉格朗日乘子，即LM(Lagarnge Multiplier)检验和平方收益率自相关的Ljung-Box检验方法得到的检验结果。

表3 两种指数的日对数收益率ARCH效应检验

检验的原假设是残差序列不存在ARCH效应，由表3可知，两种指数的ARCH-LM检验和ARCH-Ljung-Box检验的滞后阶数都为13，对应的p-value值都小于2.2e-16，即在99%的显著性水平上拒绝不存在ARCH效应的原假设，两种指数的日对数收益率序列残差都存在ARCH效应，即GARCH效应，可以进行GARCH模型的拟合。

2.8 GARCH(1，1)模型和APARCH(1，1)模型的建立

两种指数日对数收益率序列的非正态性、平稳性、弱自相关性及残差序列的ARCH效应都表明，美国股市两种指数的日对数收益率序列都可以用GARCH模型拟合。假设在日对数收益率满足正态分布和学生t分布的条件下，分别利用GARCH(1，1)模型和APARCH(1，1)模型对其进行拟合，并对两种指数满足两种分布下的两个模型进行比较。表4和表5分别是两种指数在GARCH(1，1)模型和APARCH(1，1)模型下的系数值与p值。

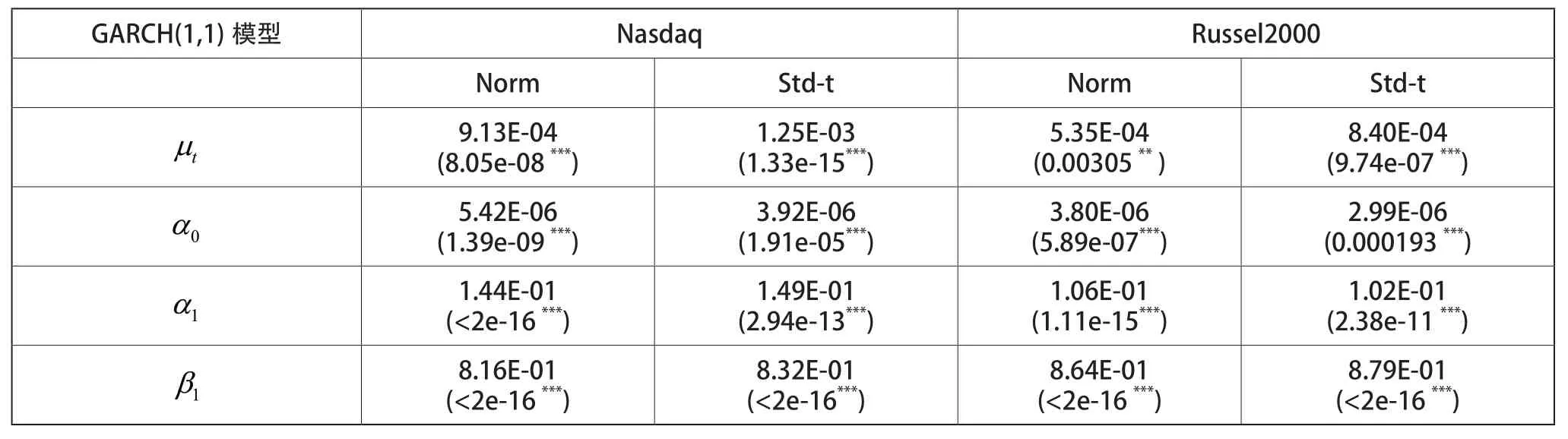
表4 两种指数日对数收益率GARCH(1，1)模型下的系数值与p值

表5 两种指数日对数收益率APARCH(1，1)模型下的系数值与p值

由表4和表5可以得出两种指数在满足正态分布及学生t分布下的GARCH(1，1)模型和APARCH模型(1，1)表达式，本文将根据已建立的模型对两种指数日对数收益率的波动率进行拟合及预测。

2.9 模型对比分析

完成上述模型的建立后，需对两种模型的拟合效果进行对比分析。表6和表7分别为两种指数日对数收益率满足正态分布和学生t分布的GARCH模型和APARCH模型的选择信息。

表6 两种指数日对数收益率GARCH(1，1)模型的选择信息

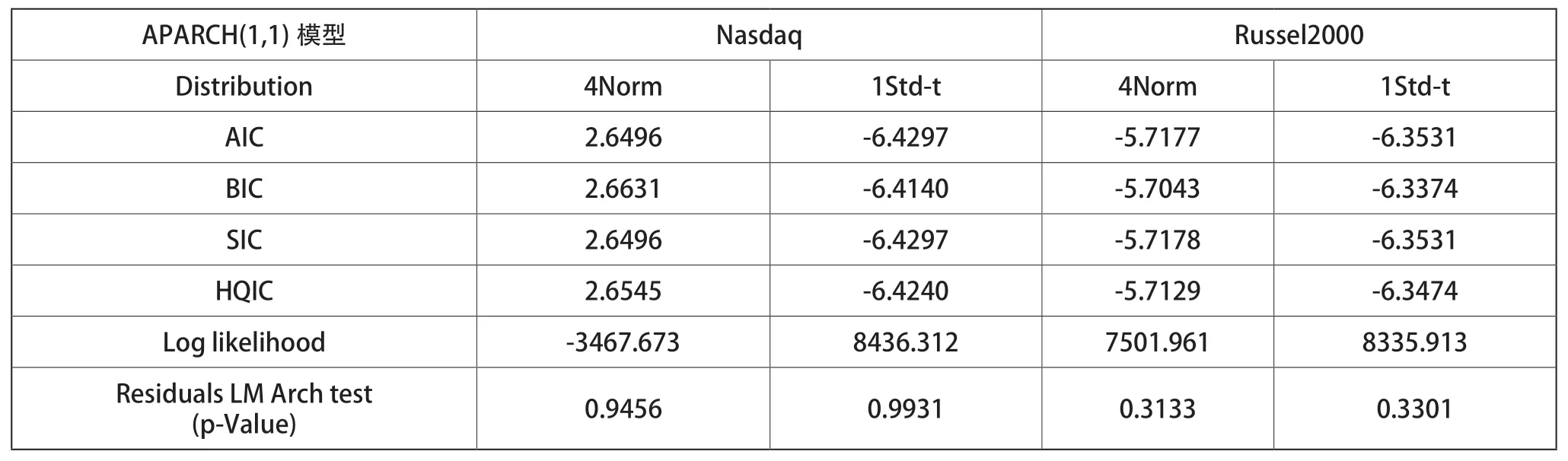
表7 两种指数日对数收益率APARCH(1，1)模型的选择信息

由表6和表7可知：

第一，由两种指数AIC准则、SIC准则，以及对数似然准则即Log likelihood值由大到小依次为满足学生t分布的APARCH模型、满足学生t分布的GARCH模型、满足正态分布的GARCH模型、满足正态分布的APARCH模型。因此，两种指数最佳分布下的模型均为满足学生t分布的APARCH模型，最差分布下的模型均为满足正态分布的APARCH模型。

第二，满足学生t分布的GARCH模型优于正态分布下的GARCH模型，满足学生t分布的APARCH模型优于正态分布下的APARCH模型。因此，学生t分布比正态分布更适合对收益率的拟合，验证了上文结论。

第三，建模完成后，对残差序列再次进行LM检验，由最后一行可知，检验的p-Value值都远大于0.01，且在APARCH模型下的Nasdaq指数的p值超过了0.9，因此两种指数日对数收益率在GARCH模型和APARCH模型下都是可行的，满足学生t分布的APARCH(1，1)模型的拟合最优，尤其是对Nasdaq指数收益率的拟合。

2.10 波动率预测

对于波动率较大的资产，价格的变动范围很大；对于波动率较小的资产，价格更稳定。对交易者来说，波动率为高回报创造了机会。当波动率较高时，意味着更大的操作空间，高抛低吸可以给投资者带来较高收益，但同时高波动率也增加了损失。本文运用满足学生t分布的APARCH(1，1)模型对Nasdaq指数和Russel2000指数的波动率进行超前三步预测，预测结果分别如图5和图6所示，蓝色曲线为波动率真实值走势变化，黄色曲线为波动率预测值走势变化。由5和图6可知，两种指数在2020年10月14日—2020年10月29日均呈现低波动率现象，且Nasdaq指数波动率最大值大于0.020，Russel2000指数数波动率最大值接近0.016，验证了上文Russel2000的风险相对较低，更适合投资这一结论。同时，波动率预测值可为未来投资提供参考。

图5 Russel2000指数波动率预测结果图

图6 Nasdaq指数波动率预测结果图

3 结语

本文选取美国股市的Nasdaq指数和Russel2000指数作为样本数据，借助统计软件，利用GARCH族模型对两个股指的波动性特征进行实证分析。实证结果表明：(1)美国股市长期处于波动上升期，市场调节灵活度高，且Russel2000指数的风险较Nasdaq指数更稳定，更适合投资；(2)两种指数都在2011年和2019年下半年呈高波动周期，并在2019年下半年达到最大幅度波动，所以美国股市存在波动聚类现象和非正态性，且两种指数日收益率序列的方差是时变的；(3)两种指数日对数收益率序列都具有非正态性、平稳性、弱自相关性及残差序列的ARCH效应，都可用GARCH模型和APARCH模型拟合，尤其是满足学生t分布的APARCH模型的拟合效果更优，且得到的两种指数波动率的预测值可以为未来投资提供参考。