让素养在活动中发展

周庆红

数学综合与实践主题活动是在实际生活背景下探寻数学学科内在规律的数学活动，它有利于提高学生的数学综合实践能力、问题解决能力和创新意识。数学课程标准鼓励教师聚焦数学知识的综合运用，以融合其他学科知识的实际情境和真实问题为切入点，自主制定活动主题，设计具有可操作性的实践活动。笔者以六年级数学综合与实践主题活动“有趣的平衡”为例，分析跨学科的活动设计策略，阐述抓住关键问题“杠杆支点和刻度如何确定”“怎样挂钩码可以使杠杆平衡”，引导学生设计实验方案，经历“杠杆原理”的探究过程，解决简单的实际问题，最终学会从数学角度解释生活现象的教学过程。

一、把握认知起点，拓宽活动渠道

为了解学生的学习起点，笔者设计了包含3个问题的课前测试。

问题1：你在生活中见过哪些应用杠杆的实例，请用文字说明或用画图的方式表示出来。此题考查学生在科学课所学的认识杠杆的情况。

问题2提供了生活中常见的杠杆应用场景图（如图1），让学生判断起瓶器、钢笔、取餐夹、锤子、筷子、核桃夹等是省力杠杆还是费力杠杆。此题考查學生在科学课所学的理解省力杠杆与费力杠杆的情况，以及学生的生活经验。

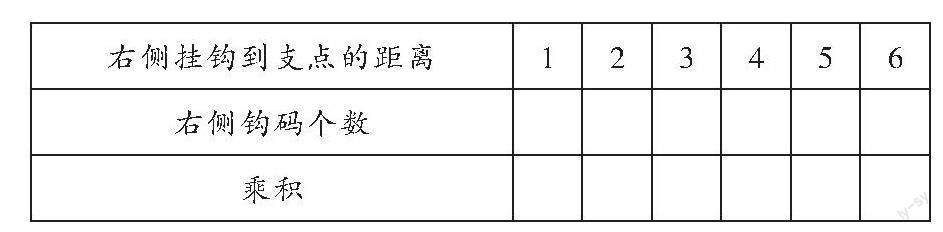
问题3：如图2所示，在杠杆支点左侧固定位置挂上砝码，要使它保持平衡，可以分别在右侧的1，2，3，4，5，6处挂几个钩码？右侧挂钩到支点的距离和右侧钩码个数成什么关系？此题主要考查学生对科学实验仪器的了解情况，以及对平衡现象的感知情况。

测试数据显示：对于问题1，80%的学生能通过图形或文字描述生活中杠杆的应用场景；对于问题2，54%的学生能找到两个省力杠杆，但无法理性分析省力原理，83.3%的学生难以理解费力杠杆；对于问题3，22%的学生能正确填写如下表格，发现右侧挂钩到支点的距离与右侧钩码个数成反比例关系，其中，4%的学生能规范表述左侧挂钩到支点的距离和左侧钩码个数的乘积一定时，右侧挂钩到支点的距离和右侧钩码个数成反比例关系。

基于以上调查结果，笔者确定了“制作杠杆—利用自制杠杆探究规律”的实践探究路径，引领学生探索“杠杆原理”背后隐藏的数学原理，以体现数学、科学、物理学三门学科之间的联系，培养学生的综合素养，提高他们分析、解决复杂问题的能力。这样设计，学生在解决问题的过程中不仅能体验到学科交叉的魅力，提升跨学科应用能力，还能增强信息收集和处理能力，开阔数学视野。

二、创新教学方法，提升综合素养

“杠杆原理”与现行教育科学出版社发行的六年级上册《科学》教材中《杠杆的知识》联系紧密，笔者以学生在科学课中习得的杠杆的结构、功能、基本操作等知识、经验为基础，设计本综合实践活动，引导学生从数学的角度研究“杠杆原理”。本活动的核心问题是“怎样挂钩码可以使杠杆平衡”。考虑到六年级学生用标准的杠杆尺探究平衡规律缺乏挑战性，笔者将教材原有内容设计成两课时的跨学科主题活动，以更好地发展学生的综合实践能力。

第一课时，笔者引导学生完整经历制作杠杆的实践环节，并在小组活动中交流实验结果、调整实验策略，初步养成理性思考的思维品质，增强思维的周密性、全面性。制作杠杆的过程中最难的是确定支点和刻度，笔者巧妙运用学生在课堂上生成的资源——很多学生先从木棍一端开始等距离标记刻度，然后在中点处提起杠杆，发现有些杠杆并不平衡——做进一步点拨，引导学生自主探究确定刻度的正确方法。经过师生互动、生生交流，学生发现中点不是支点的木棍要先找到平衡点，将平衡点确定为支点，再从支点处往两边标记刻度，如此才能制作出科学的杠杆。教学中，笔者鼓励学生提出问题，引导学生在试错中自主探究出解决问题的途径，使学生有了更多发展创造性思维的机会，在跨学科学习中提升了思辨能力和创新意识。

三、注重学习体验，凸显自主探究

第二课时，学生用自制的杠杆探究杠杆平衡的规律。笔者提问：“怎样挂钩码可以使杠杆平衡呢？”学生自由发表想法后，笔者让学生拿出自制的杠杆进行实验验证，并按照如下活动要求操作：组长明确分工，人人参与；用下表记录数据，验证猜想；发现规律，汇报交流。

各小组学生合理分工，根据实验要求确定几组数据后进行实验验证，并在上表中记录相关数据。笔者参与到学生的实验中，了解学生的实验情况，发现学生的实验数据比较单一，便给予学生提示和指导。学生完成多组数据的验证后，笔者让学生汇报实验过程和结果，并思考“这些不同的数据有什么相同之处”。学生汇报：“我们猜想的第一组数据是杠杆左边刻度数为4、钩码数为3，右边刻度数为6、钩码数为2，经过实验，发现杠杆平衡……”这样汇报了4组数据的实验结果后，学生提出：“当左边钩码数与左边刻度数的乘积等于右边钩码数与右边刻度数的乘积时，杠杆平衡。”学生汇报后，笔者出示不同小组的实验数据与结论，并质疑：“为什么各组所记录的左右两边的刻度数和钩码数都不同，却发现了相同的规律？”通过交流，学生对平衡规律的认识从模糊到清晰，形成了“‘左边刻度数×左边钩码数=右边刻度数×右边钩码数时杠杆平衡”的结论。在此基础上，笔者引导学生明确“在实际运用时，钩码数相当于物体质量，刻度数就是支点到两边挂钩处的距离”，帮助学生进一步构建“左边质量×左边距离=右边质量×右边距离”这一杠杆平衡模型。这个过程既提升了学生分析问题、解决问题的能力，又让学生体验到合作学习的乐趣。

（作者单位：黄石市下陆小学）

责任编辑  刘佳