Blockchain-Based Certificateless Bidirectional Authenticated Searchable Encryption Scheme in Cloud Email System
2024-03-23YanzhongSunXiaoniDuShufenNiuandXiaodongYang
Yanzhong Sun ,Xiaoni Du,⋆ ,Shufen Niu and Xiaodong Yang
1College of Mathematics and Statistics,Northwest Normal University,Lanzhou,730070,China
2College of Computer Science and Engineering,Northwest Normal University,Lanzhou,730070,China
ABSTRACT Traditional email systems can only achieve one-way communication,which means only the receiver is allowed to search for emails on the email server.In this paper,we propose a blockchain-based certificateless bidirectional authenticated searchable encryption model for a cloud email system named certificateless authenticated bidirectional searchable encryption(CL-BSE)by combining the storage function of cloud server with the communication function of email server.In the new model,not only can the data receiver search for the relevant content by generating its own trapdoor,but the data owner also can retrieve the content in the same way.Meanwhile,there are dual authentication functions in our model.First,during encryption,the data owner uses the private key to authenticate their identity,ensuring that only legal owner can generate the keyword ciphertext.Second,the blockchain verifies the data owner’s identity by the received ciphertext,allowing only authorized members to store their data in the server and avoiding unnecessary storage space consumption.We obtain a formal definition of CL-BSE and formulate a specific scheme from the new system model.Then the security of the scheme is analyzed based on the formalized security model.The results demonstrate that the scheme achieves multikeyword ciphertext indistinguishability and multi-keyword trapdoor privacy against any adversary simultaneously.In addition,performance evaluation shows that the new scheme has higher computational and communication efficiency by comparing it with some existing ones.
KEYWORDS Cloud email system;authenticated searchable encryption;blockchain-based;designated server test;multi-trapdoor privacy;multi-ciphertext indistinguishability
1 Introduction
Email systems have become an essential component of modern communication tools and revolutionized the way we conduct business,education,and personal communication,facilitating effective and efficient communication.However,the widespread usage of email has raised significant concerns regarding email security.Searchable encryption[1],as a promising security solution,has been successfully applied in many fields,including email systems.It can not only provide users with convenient search and data management methods while preserving data privacy and security but also enrich the overall user experience while safeguarding email confidentiality.That is,searchable encryption technology has become an indispensable security protection measure within email systems.
Public key Encryption with Keyword Search(PEKS)is a form of searchable encryption within the asymmetric category proposed by Boneh et al.[2]which optimises the security and privacy of email and improves users’experience and the system performance.Since then,several PEKS schemes with varying functionality have been proposed including secure channel-free PEKS [3] and certificateless PEKS[4,5].Although these schemes offer numerous keyword search methods suitable for encrypted email systems,there are still some security issues to be concerned with,specifically the Keyword Guessing Attack(KGA)[6].In fact,the limited keyword space and low entropy render most PEKS schemes vulnerable to both online and offline KGA.
To defend against KGA,Huang et al.[7] introduced the Public Key Authenticated Encryption with Keyword Search (PAEKS) as a new variant of PEKS in 2017 and proved that the proposed PAEKS scheme achieved Ciphertext Indistinguishability (CI)-secure and Trapdoor Privacy (TP)-secure.Considering against chosen multi-keyword attacks and multi-keyword guessing attacks,Qin et al.[8]presented a new security model as Multi-Ciphertext Indistinguishability(MCI)in 2020 and Pan et al.formalized Multi-Trapdoor Privacy(MTP)in[9],which are the enhancement of CI-secure and TP-secure,respectively.
It is obvious that all PEKS/PAEKS systems cannot avoid the inherent burden of certificate management and key escrow issues due to their reliance on public key infrastructure cryptosystem or identity-based cryptosystem.A common approach to overcome these problems is to incorporate the PEKS/PAEKS system in certificateless public key cryptography (CL-PKC) [10].As a result,Peng et al.[5] proposed the first certificateless PEKS scheme and He et al.[11] developed the first certificateless PAEKS scheme.However,the CL-PKC scheme still suffers from two types of attackers.The distributed nature of blockchain makes it impossible to tamper the data stored on the chain,which solves the trust problem and guarantees data security.Therefore,in CL-PKC,in order to avoid forgery attacks launched by attackers using public parameters,part of the user’s private key is created by a blockchain smart contract[12].
All of the above improvements to PEKS/PAEKS including the enhancement of security and the introduction of certificateless cryptosystem have significantly optimized their application for protecting the data security and privacy,enhancing user experience and improving system performance.Moreover,Zhang et al.[13] highlighted a crucial aspect of encrypted email systems: users must not only search for encrypted emails received from others but also retrieve encrypted emails sent to others,and they developed a new cryptographic approach named Public-key Encryption with Bidirectional Keyword Search (PEBKS).Inspired by the above ideas,it is imperative to develop a certificateless authenticated bidirectional searchable encryption scheme with a designated server test that can achieve both MCI and MTP security.
1.1 Our Contributions
The following is a list of the main contributions of this paper:
• Considering the actual application scenario of cloud email system that the data owner also needs to retrieve emails with target keywords.We apply the bidirectional searchable functionality to CL-PAEKS cryptosystem by introducing a trapdoor generation algorithm for the data owner,put forward a cryptographic concept named CL-BSE.This allows the data owner not only to encrypt and send an email to the cloud email server,but also to generate its own trapdoor for specified keyword and retrieve the corresponding email.
• On the one side,the scheme in this paper achieves bidirectional searchable functionality,on the other side,it establishes dual authentication functions.In the process of generating the ciphertext with the keyword,the data owner not only uses the public key of the data receiver,but also uses his own private key.Similarly,the data receiver uses both his own private key and the public key of the data owner to generate the corresponding trapdoor,which authenticates the identity of the data owner.Meanwhile,the blockchain can also verify the legitimacy of the ciphertexts,which effectively saves the storage space.Furthermore,the scheme satisfies designated server test which makes secure channel free.
• We formalize the definition of the new cryptographic concept CL-BSE,then give a concrete construction of the scheme under the bilinear pairing.Meanwhile,we formally define the security model of CL-BSE scheme and show that in the random oracle model,it is able to achieve both MCI and MTP security levels against inside KGA under the CBDH hardness assumption.Through the experimental comparison,our scheme has more advantages and higher efficiency in computation and communication costs.
1.2 Organization
The rest of this paper is arranged as follows.The next section presents some basic symbols and notations,including bilinear pairing and hardness assumption.Section 3 illustrates the framework of our scheme including the system model in 3.1,the formalized definition in 3.2 and the formalized security model in 3.3.Section 4 is the concrete construction of our CL-BSE scheme and Section 5 guarantees the security of the new scheme.In Section 6,we analyze the performance by comparing it with existing works.Eventually,we draw a conclusion of the paper in Section 7.
1.3 Related Works
Boneh et al.[2]presented the first PEKS scheme in 2014,which effectively solved the distribution and management of the secret-key in the symmetric searchable encryption(SSE)cryptosystem[14–16].However,Baek et al.[3]pointed out that the trapdoor transmission channel must be secure in[2],and then proposed a secure channel free PEKS(SCF-PEKS)scheme by giving the server a public/private key pair so that only the designated server could execute the test algorithm.Rhee et al.in[17]improved the trapdoor security of[3]and then constructed a new SCF-PEKS scheme called dPEKS under the new security model.Nevertheless,Byun et al.[6] claimed that both PEKS and SCF-PEKS schemes were vulnerable to(offline)KGA and a variety of improved PEKS and SCF-PEKS schemes[18–20]were proposed to overcome the series security threats in the years including [17].Unfortunately,it turns out that none of them can really resist the offline KGA[21].What’s worse is that Yau et al.[22]pointed out that these existing PEKS schemes suffered from another generic attack called online KGA or inside KGA in 2013.
In order to defend against both online KGA and offline KGA,Huang et al.[7] introduced a new primitive of PAEKS and proposed the first PAEKS scheme in 2017.The essence of PAEKS is to insert the data owner’s public/private key pair into PEKS so that it can authenticate the keyword while encrypting it.Meanwhile,they defined the security as TP and CI for trapdoor and ciphertext,respectively.After that,Noroozi et al.[23] pointed out some weaknesses of the previous security in terms of multi-user settings.In 2020,Qin et al.[8] found that the CI &TP security in [7] does not protect the information whether two different files extract identical keywords or the same file contains how many identical keywords so they improved the security model as MCI,and they proposed a PAEKS scheme satisfying MCI instead of MTP.In 2021,Pan et al.claimed that their new scheme in[9]achieved both MCI and MTP secure until Cheng et al.[24]presented an effective attack method on MTP.In addition to the security efforts,contributions to the functionality of PEKS/PAEKS have also been made.Fuhr et al.[25]and Hofheinz et al.[26]inserted the ciphertext decryptable function on PEKS schemes in different types of models.Zhang et al.[13]observed that in practical application,a data owner also needed to retrieve encrypted files containing specified keywords,then proposed a cryptographic system Public-key Encryption with Bidirectional Keyword Search (PEBKS) and constructed a concrete scheme.
All of the above schemes,including PEKS,PAEKS and PEBKS are identity-based cryptosystem with key escrow and certificate management issues.Peng et al.[5]constructed the first PEKS under CL-PKC named CLPEKS.In 2018,Ma et al.[4]proposed an improved CLPEKS scheme and it was improved again in the literature[27],which was been pointed out cannot achieve both MCI and MTP secure and was subsequently improved by Yang et al.[28].But,the cryptanalysis in[29]demonstrates that these CLPEKS frameworks also suffer from the security vulnerability caused by the keyword guessing attack and in order to remedy these security weakness and provide resistance against both inside and outside keyword guessing attacks,they propose a new CLEKS scheme by embedding the owner’s private key into the calculation of keyword ciphertexts,which actually is CL-PAEKS.Later,combining[4],He et al.[11]proposed a CL-PAEKS scheme,and Shiraly et al.[30]constructed a pairing-free CL-PAEKS.However,their security and functionality still need to be improved and promoted.
2 Preliminaries
2.1 Notations
The symbols and notations used in this paper are presented in the Table 1.

Table 1:The symbols and notations
2.2 Bilinear Pairing
Bilinear pairing[31]is an important tool in the construction of many pairing based cryptographic schemes,including our CL-BSE scheme,and we usually construct it using the Weil pairing and the Tate pairing[31–33].
Definition 2.1(Bilinear Pairing).Let G1be an additive cyclic group of large prime orderqand G2a multiplicative cyclic group of the same order.Abilinear pairing:G1×G1→G2is a mapping which satisfies the following properties:
Bilinearity:For anyP,Q∈G1and anya,;
Non-Degeneracy:There exists aP∈G1such that,(wheredenotes the identity in G2).Observe that since G1and G2are groups of prime order,so for any generatorP∈G1,this statement implies that∈G2is a generator of G2;
Computability:For anyP,Q∈G1,there is an efficient algorithm to compute.
2.3 Hardness Assumption
where the probability is taken over the random choices ofP∈G1,a,b,c∈and the random coins tossed byB.
3 The Framework
There are three principal works in this section.First,we illustrate the system model of our protocol in this paper based on[13],and then formalise the definition of our CL-BSE scheme.Finally,we define the security model based on[8,9].
3.1 System Model
As shown in Fig.1,the system model of our protocol includes the following five parties: cloud email server (CS),smart contract-based key generation center (SC-KGC),blockchain (BC),data owner(DO)and data receiver(DR).They are interacting as follows:
•SC-KGC:Deployed on the blockchain,the smart contract key generation center is a combination of a smart contract and a conventional key generation center.It is responsible for producing and storing the public parameters on the blockchain,generating and distributing partial private keys and the master key to the corresponding parties.
•Blockchain:To avoid the system public parameters being tampered with,blockchain stores and then transmits them to all clients.The blockchain is also responsible for verifying the validity of the ciphertext,and then transferring the verified ciphertext to the cloud server.
•Cloud Email Server:The cloud email server plays an “honest but curious”role in the system model,i.e.,it stores the real data,retrieves keyword sets by rules and returns the corresponding results correctly.Meanwhile,it may launch keyword guessing attacks on a set of received search tokens.Furthermore,it also performs the test algorithm and then sends the search results to the data receiver.
•Data Owner:The data owner is a client who wants to store the encrypted data files with keyword indexes in the email server while sending it to the data receiver through the cloud email server,so that he/she can retrieve it by generating a trapdoor using his/her own private key.
•Data Receiver:The data receiver is one who receives emails from the cloud email server by sending a trapdoor for the keywords he/she interested in using his/her own private key.
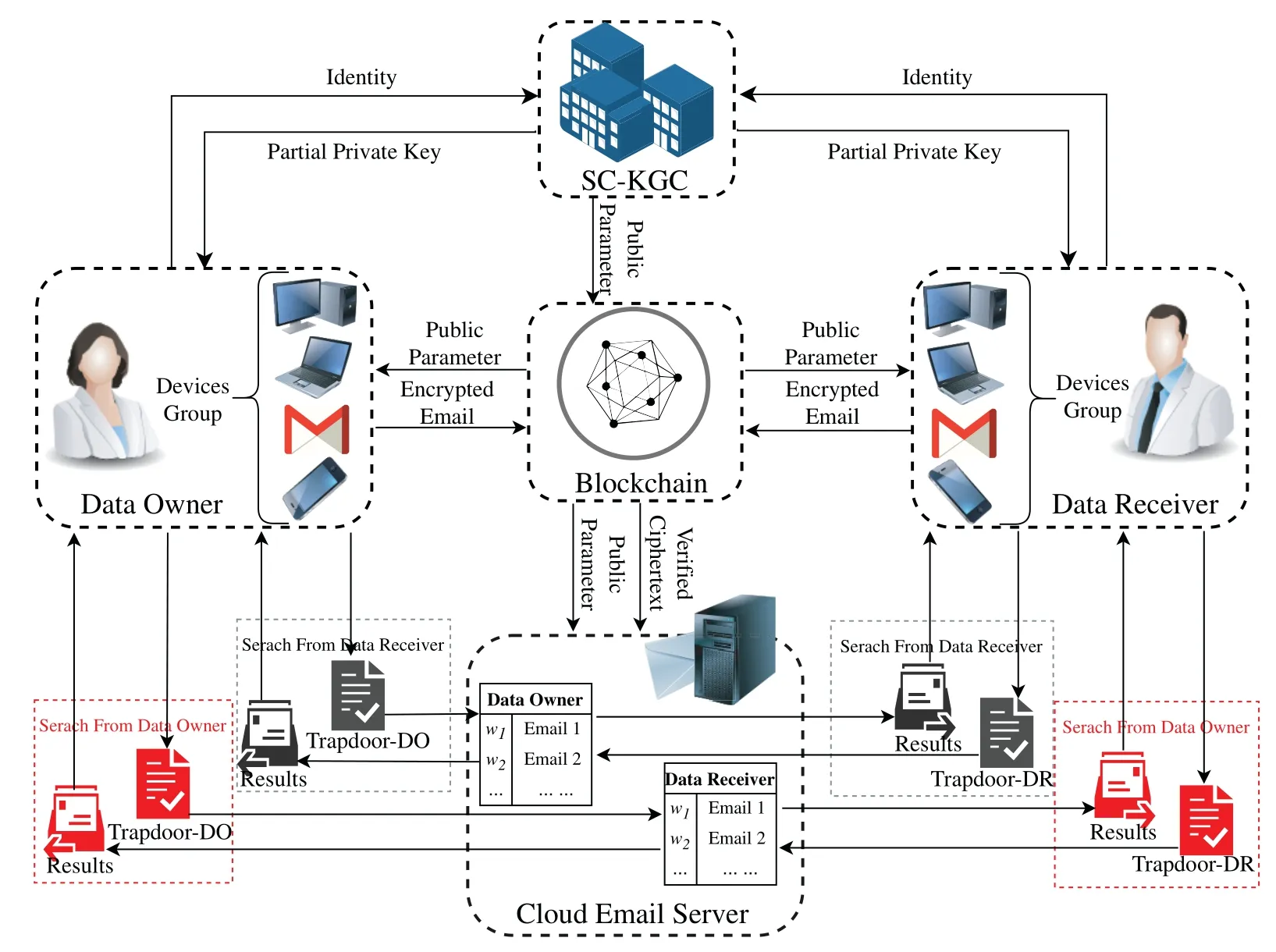
Figure 1:System model
3.2 The Definition of CL-BSE
We have formalized the architecture of our certificateless bidirectional authenticated searchable encryption(CL-BSE)scheme for the cloud email system.
Definition 3.1.The CL-BSE scheme consists essentially of nine PPT algorithms:Setup,Extract-PPK,Set-secret-value,Set-private-key,Set-public-key,CL-BSE,Trapdoor-DR,Trapdoor-DO and Test.They are described below:
• Setup(1k):This algorithm is executed by SC-KGC.Given a security parameter 1k,the algorithm generates the global public parametersParamsand the master keyPmas.
• Extract-PPK (Params): This algorithm is also performed by SC-KGC.It takes as input the global public parametersParams,the master keyPmasand the client identityIDU(U∈{CS,DO,DR}),generates and outputs each client’s partial private keyPPKU.
• Set-secret-value(Params,IDU):This algorithm is run by each client.InputParamsand the client identityIDU(U∈{CS,DO,DR}),it generates the secret valueSVUfor each participant.
• Set-private-key (Params,SVU,PPKU): Each client runs this algorithm on its own.EnteringParams,secret valueSVUand partial private keyPPKU,it outputs the private keySKUfor each client.
• Set-public-key(Params,SVU):This algorithm is executed by each client.It takes as inputParamsand the secret valueSVU,and outputs the public keyPKUfor itself.
• CL-BSE (PKDR,PKCS,SKDO,w): This is the keyword ciphertext generation algorithm and is performed by the data owner.It takes as inputPKDR,PKCS,SKDOand keywordwwith respect to the encrypted files,outputs a ciphertextCw.
• Trapdoor-DR (PKDO,PKCS,SKDR,w′): This algorithm generates trapdoor for data receiver.When searching the encrypted files containing the keywordw′from the cloud email server,it takes as inputPKDO,PKCS,SKDRand the keywordw′,and outputsTDR.
• Trapdoor-DO(PKDR,PKCS,SKDO,w′):This algorithm generates trapdoor for data owner.When the client wants to retrieve the encrypted files containing the keywordw′from the cloud email server,it takes as inputPKDR,PKCS,SKDOand the keywordw′,outputsTDO.
• Test (Cw,SKCS,Tw′=TDO(TDR)): The test algorithm is executed by the cloud email server.It takesCwandTw′as input and returns“1”ifw=w′and“0”otherwise.
Correctness.The correctness of our CL-BSE scheme is defined as follows.For any legally registered clientsIDU(U∈{DO,DR,CS})with public/private key pairs(PKU,SKU).LetCw←CL-BSE(PKDR,PKCS,SKDO,w)be the ciphertext ofw,TDO←Trapdoor-DO(PKDR,PKCS,SKDO,w′)andTDR←Trapdoor-DR(PKDO,PKCS,SKDR,w′)be the trapdoors ofw′generated byDOandDR,respectively.Correctness implies
3.3 Security Model
As with other certificateless cryptosystems [5,10,28,34,35],the CL-BSE scheme considers two types of adversary with different privileges: Type-I adversaryA1and Type-II adversaryA2.Specifically,
•Type-I adversaryA1.It plays the part of the malicious user who is available to perform queries including extract partial private key,request public key,extract secret value and replace public key,but does not have access to the master private keyPmas.
•Type-II adversaryA2.It models an honest-but-curious SC-KGC that has access to the master private keyPmas,but not allowed to replace public key query.
Now,the above queries are listed as follows,which are actually interactions between an adversaryA1(A2)and a challengerC.
–Extract-PPK query.WhenA1(A2)queries partial private key for identityIDi,Cexecutes Extract-PPK algorithm and returns partial private keyPPKi.
–Extract-secret-value query.WhenA1(A2)queries secret value for identityIDi,Cexecutes Setsecret-value algorithm and returns a secret valueSVi.
–Request-public-key query.WhenA1(A2)queries public key for identityIDi,Cexecutes Setpublic-key algorithm and returns public keyPKi.
–Replace-public-key query.A1is permitted to askCto replace the publicPKiwith a new onefor any userIDi.
–Ciphertext query.WhenA1(A2)queries the ciphertext of the keywordw,the challengerCreturns the matching ciphertextCw.
–Data receiver trapdoor query.WhenA1(A2)queries the data receiver trapdoor of keywordw′,Creturns the matching trapdoorTDR=.
–Data owner trapdoor query.WhenA1(A2)queries the data owner trapdoor of keywordw′,Creturns the matching trapdoorTDO=.
In order to capture chosen multi-keyword attacks and multi-keyword guessing attacks,the security model of our CL-BSE scheme are defined as MCI[8]and MTP[9],which are the enhancement of CIsecure and TP-secure[7],respectively.Their formal definitions are described by the following games,which are interactions between an challengerCand an adversaryA1orA2.
Game 1:The MCI Security against AdversaryA1.
•Setup.Given security parameter 1k,Cgenerates public parameterParamsand system master keyPmasby running Setup algorithm.It then responds only toA1Paramsand keeps master keyPmassecret.
•Phase 1.A1can adaptively perform a series of polynomial times queries,includingExtract-PPKquery,Extract-secret-valuequery,Request-public-keyquery,Replace-public-keyquery,Ciphertextquery,Data receiver trapdoorquery andData owner trapdoorquery.
•Challenge.AfterA1finishes the queries inPhase 1,it selects two challenge keyword sets={w0,1,w0,2,...,w0,n},={w1,1,w1,2...,w1,n} which are not queried inPhase 1and sends them toC.After that,it first chooses a random bitb∈{0,1},then computes the searchable ciphertextwith respect to.Finally,it returnsas a challenge ciphertext.
•Phase 2.As inPhase 1,A1can continue to make series queries for polynomial times and the restriction here is that cannot make ciphertext query and two trapdoor queries on.
•Guess.Finally,A1outputs its guessb′∈{0,1}onb,and wins this game ifb′=b.
The following probability equation definesA1’s advantage in the game,
Game 2:The MCI Security against AdversaryA2.
•Setup.Given security parameter 1k,Cruns Setup algorithm generates public parameterParamsand system master keyPmas,then sends bothParamsandPmastoA2.
•Phase 1.As inGame 1,A2can makeExtract-PPKquery,Extract-secret-valuequery,Requestpublic-keyquery,Ciphertextquery,Data receiver trapdoorquery andData owner trapdoorquery,but not available forReplace-public-keyquery.
•Challenge.WhenA2completed thePhase 1,it selectsas challenge keywords sets like the steps inGame 1,and sends them toC.ThenCchooses a random bitb∈{0,1}and generates the ciphertextwith respect to.Finally,it returnstoA2as a challenge ciphertext.
•Phase 2.This phase is the same asGame 1,A2is not allowed to make ciphertext query and two trapdoor queries on.
•Guess.Finally,A2outputs its guessb′∈{0,1}onb,and wins ifb′=b.
The advantage ofA2inGame 2is defined by the following probability equation:
Definition 3.2(MCI security).The CL-BSE scheme is said MCI security if for any PPT adversaryA,its advantagesagainst the challengerCinGame 1andGame 2are negligible.
Game 3:The MTP Security against AdversaryA1.
•Setup.The setup algorithm is the same asGame 1,Calso only sends the public parameterParamstoA1eventually.
•Phase 1.Same as processPhase 1inGame 1.
•Challenge.WhenA1has finished thePhase 1,do the same as that inGame 1to obtain two challenge keywords setsand send them toC.After that,Cchooses a random bitb∈{0,1}first,then computes the trapdoorwith respect to.Finally,it returnstoA1as a challenge trapdoor.
•Phase 2.Same as processPhase 2inGame 1.
•Guess.Finally,A2outputs its guessb′∈{0,1}onb,and wins this game ifb′=b.
The advantage ofA1inGame 3is defined by
Game 4:The MTP Security against AdversaryA2.
•Setup.The setup algorithm is the same asGame 2,the challengerCsends both the public parameterParamsand the master keyPmastoA2eventually.
•Phase 1.Same as processPhase 1inGame 2.
•Challenge.AfterA2has finished thePhase 1,do the same as that inGame 3to obtain two challenge keyword setsand send them toC.ThenCchooses a random bitb∈{0,1}and generates the trapdoorwith respect to.Finally,it returnstoA2as a challenge trapdoor.
•Phase 2.Same as processPhase 2inGame 2.
•Guess.Finally,A2outputs its guessb′∈{0,1}onb,and it wins this game ifb′=b.
The advantage ofA2inGame 4is defined by
Definition 3.3(MTP security).The CL-BSE scheme is said MTP security for both data receiver trapdoor and data owner trapdoor,if for any PPT adversaryA,its advantagesandagainst the challengerCinGame 3andGame 4are negligible.
4 The Proposed CL-BSE Scheme
In this section,we give a concrete construction as the formal definition of the CL-BSE scheme in Section 3.2 with a designated server,it consists of nine PPT algorithms in five phases: System initialization,Key generation,Keyword encryption,Trapdoor generation and Test.
Phase A.System Initialization.
• Setup(1k):Given the security parameter 1k,SC-KGC performs the following steps:
(1) Select a cyclic additive group G1,a cyclic multiplicative group G2with a large prime orderq,(q >2k)and three generatorsP1,P2andQ∈G1,generate a bilinear pair:G1×G1→G2;
(2) Pick a random numbers←,put it as the system master key and store it secretly,then computePpub=sP1;
(3) Define six different cryptographic hash functionsHi(1≤i≤6)as:H1: {0,1}∗→G1,H2:{0,1}∗×G1→,H3:{0,1}∗×G1×G1×G1→,H4:G1→{0,1}len,wherelenis the fixed length output,H5: G2→,H6: {0,1}logw+len→,and logwdenotes the length ofw;
(4) Broadcast the public parametersparams=on the blockchain.
Phase B.Key Generation.
• Extract-PPK(Params):SC-KGC takes as input the public parametersParams,the master keyPmasand the identityIDU(U∈{CS,DO,DR}),then generates partial private keys for all clients as follows:
(1) ForCS,SC-KGC selectsrCS←randomly,computesRCS=rCSP2,αCS=H2(IDCS,RCS)anddCS=rCS+αCSs(mod ∼q),and outputsPPKCS=(RCS,dCS)as its partial private key;
(2) ForU∈{DO,DR},SC-KGC computes their partial private key asPPKU=DU,whereDU=sQUandQU=H1(IDU).
• Set-secret-value(Params,IDU):The clientU∈{DO,DR}selectsxU,yU←randomly and setsSVU=(xU,yU).CSselects a single random numberxCS←and setsSVCS=xCS.
• Set-private-key (Params,SVU,PPKU): The clientU∈{DO,DR} andCSset their own private keys asSKU=(xU,yU,DU)andSKCS=(xCS,dCS),respectively.
• Set-public-key(Params,SVU):The clientU∈{DO,DR}computesPU=xUP1,YU=yUQ,and assigns its public keys asPKU=(PU,YU),whileCSassigns its public key asPKCS=(PCS,RCS),wherePCS=xCSP2.
Phase C.Keywords Encryption.
• CL-BSE(PKDR,PKCS,SKDO,w):WhenDOwants to encrypt the keywordwextracted from the encrypted emails,he/she enters the relevant parametersparams,SKDO,IDDR,PKDR,IDCS,PKCSand performs the following steps:
(1) ComputeαCS=H2(IDCS,RCS),βCS=H3(IDCS,Ppub,PCS,RCS);
(2) Computek1=H4(yDOYDR),k2=;
(3) Selectr←randomly,then compute
(4) ComputeV=DDO+(r·k2+xDO)RCS;
(5) Upload the ciphertextCw=(C1,C2,C3,V)on the blockchain.
Upon receivingCw=(C1,C2,C3,V)from the data owner,the blockchain verifies the owner’s legitimacy by the equation
If and only if the owner is a legal member of the system,the blockchain then stores the verified ciphertexts to the cloud server,which can effectively save storage space.
Phase D.Trapdoor Generation.
BothDRandDOcan generate their own trapdoor in the following ways:
• Trapdoor-DR (PKDO,PKCS,SKDR,w′): Input parametersParams,SKDR,PKDOandPKCS,whenDRsearches for the files containing the keywordw′,it performs the following operations:
(1) RecallαCS,βCS,andk1=H4(yDRYDO),k2=;
(2) Select a random numbertDR←and compute
(3) OutputTDR=(T1,T2).
• Trapdoor-DO (PKDR,PKCS,SKDO,w′).Different from other CL-PAEKS models,the bidirectional keyword search functionality in this paper is achieved by introducingDO’s trapdoor generation algorithm.In fact,similar toDR’s trapdoor generation process above,whenDOretrieves the data fromCS,it does not need to generate any additional variables,but simply uses its own private keySKDOandPKDR,PKCSto generate the trapdoorTDO=(T1,T2).That is,
Phase E.Test Process.
• Test(Cw,SKCS,=TDO/TDR):TakeCw,SKCS,=TDOorTDRas input,CSverifies whether
holds.Output“1”if it holds and“0”otherwise.
Actually,from the verification equation it can be seen that sincexCSanddCSare private keys secretly held by the cloud email server,then only the server holding the private key can verify the equation above,i.e.,our scheme is a bidirectional searchable encryption scheme with secure channel free for designated server verification.
Correctness.
The verification process described above demonstrates the correctness of the data owner’s trapdoor and ciphertext test,the verification with respect to the data receiver’s trapdoor is similar and we omit it.
5 Security Analysis
Based on the formal definition of security models in Section 3.3 and the CBDH hardness assumption in Section 2.3,we give the security proof of our scheme in this section.
Theorem 5.1(MCI security).In the random oracle model,our CL-BSE scheme achieves semantically MCI security against outside chosen multi-keyword attacks under the CBDH hardness assumption.
The proof of Theorem 5.1 can be achieved by the following two lemmas.
Lemma 5.1.In the random oracle model,for any PPT adversaryA1,there is an algorithmBthat can break the CBDH assumption with advantage
ifA1wins Game 1 with advantageε.
•Phase 1.A1preforms a series of queries with polynomially many times adaptively,they are
•Phase 2.As inPhase 1,A1can make a series of queries for polynomial times and it can not make ciphertext query and two trapdoor queries on any keyword in.Denote this event asE6.
Now,supposeBcan break the CBDH assumption with advantageε′,A1can make at most,qCandqTtimes queries toH1-query,Extract-PPK query,Request-public-key query,Ciphertext query and Trapdoor query,respectively,then
we have Pr[¬E6]≥2ε.Combing with(24),we get Eq.(16)and the lemma is proved.
Lemma 5.2.In the random oracle model,for any PPT adversaryA2,there is an algorithmBthat can break the CBDH assumption with advantage
ifA2wins Game 2 with advantageε.
Proof.Similar with Lemma 5.1,given an instance of the CBDH assumption(P1,aP1,bP1,cP1)∈,Bcalculates the valueby takingA2as a subroutine as follows:
•Setup.BgeneratesParams={G1,G2,,q,P1,P2=αP1,Q,Ppub,Hi(1≤i≤6)} andPmas=s∈,setsPDO=aP1,PDR=bP1,PKCS=(PCS,RCS)andSKCS=(xCS,dCS),and choosesIDI(1≤I≤)randomly as the challenge identity.Finally,it responds both(Params,PDO,PDR,PKCS,SKCS)andPmas=stoA2.
•Phase 1.A2preforms a series of queries with polynomially many times adaptively,they are
–Hash queries.A2can queryHi(1≤i≤6)random oracles.Bresponds them as same as Lemma 5.1.
–Request-public-key query.Bmaintains a list={〈IDi,xi,yi,Pi,Yi〉} to respondA2for the public key ofIDi.The interaction is the same asPhase 1in Lemma 5.1.
–Extract-private-key query.When the identityIDiis queried byA2,Bfirst checks whetherIDi=IDI.If not,it performs as follows: ifIDialready exists onin the corresponding tuples〈IDi,λi,Qi〉and〈IDi,xi,yi,Pi,Yi〉,thenBresponds toA2asSKi=(xi,yi,sQi),otherwise performsH1queryandRequest-public-key querywithIDiand retrieves the correspondingSKi=(xi,yi,sQi).IfIDi=IDI,it aborts and denotes this event asE1.
•Phase 2.This phase is same asGame 2,A2is not allowed to make ciphertext query and two trapdoor queries on.Denote this event asE5.
Now,supposeBbreaks the CBDH assumption with advantageε′,A2can make at most,qCandqTtimes queries toH1-query,Request-public-key query,Ciphertext query and Trapdoor query,respectively,thus,
we have Pr[¬E5]≥2ε,so combing with(35),we get Eq.(27)and the lemma is proved.
Theorem 5.2MTP security.In the random oracle model,our CL-BSE scheme achieves semantically MTP security against inside multi-keywords guessing attacks under the CBDH hardness assumption.
The proof of Theorem 5.2 can be achieved by the following two lemmas:
Lemma 5.3.In the random oracle model,for any PPT adversaryA1,there is an algorithmBcan break the CBDH assumption with advantage
ifA1wins Game 3 with advantageε.
Proof.The interaction process in the proof is basically the same as Lemma 5.1 except theChallengephase and theGuessphase.They are
The analysis process of the advantagesε′thatBcomputes the above problem is also same as Lemma 5.1,that is Eq.(38)holds and the lemma is proved.
Lemma 5.4.In the random oracle model,for any PPT adversaryA2,there is an algorithmBcan break the CBDH assumption with advantage
ifA2wins Game 4 with advantageε.
Proof.The interaction process in the proof is basically the same as Lemma 5.2 except theChallengephase and theGuessphase.They are
The analysis process of the advantagesε′thatBcomputes the above problem is also same as Lemma 5.2,that is Eq.(40)holds and the lemma is proved.
6 Performance Analysis
In this section,we analyze the performance of our scheme by comparing it with some existing schemes in[4,5,28–30,36,37].
First,we give some basic operations used in the scheme and the executing times of a single operation in Table 2.These times of operations are averaged over 1000 runs on a personal computer(Lenovo with Windows 10 operating system,Intel (R) Core (TM) i7 -7700 CPU @ 3.60 GHz and 8 GB RAM memory)using the Pairing-Based Cryptography(PBC)library[38]in Ubuntu10.

Table 2:Some operations and their overhead time(ms)
Figs.2–5 and Table 3 describe the computation overhead of different algorithms in each scheme.Specifically,the computational overhead in the ciphertext generation(Fig.3)of our scheme is slightly higher than[30,36].In trapdoor generation process(Fig.4),the computational overhead of the scheme is higher than [4,5,30] since the enhanced trapdoor privacy and authentication functionality.In test process (Fig.5),its computational overhead is slightly higher than in [29,30] because our scheme is server-designated,that is,the public/private key pairs of the server are involved in the operation.However,in terms of total time,the time overhead of our new scheme is only slightly higher than[30].It has some advantages when DO (or DU) retrieves emails and is more in line with practical application scenarios.
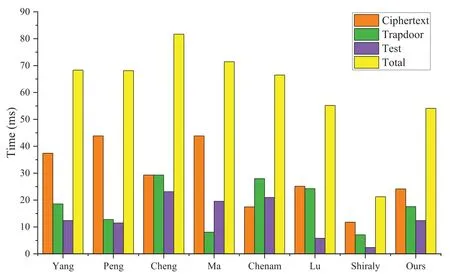
Figure 2:Computation overhead in each phase

Table 3:The computational overhead of the schemes(ms)
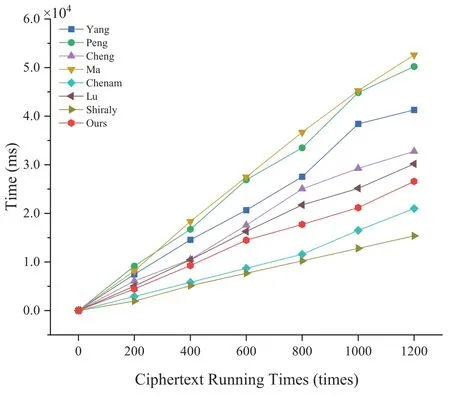
Figure 3:Running time of encryption

Figure 4:Running time of trapdoor
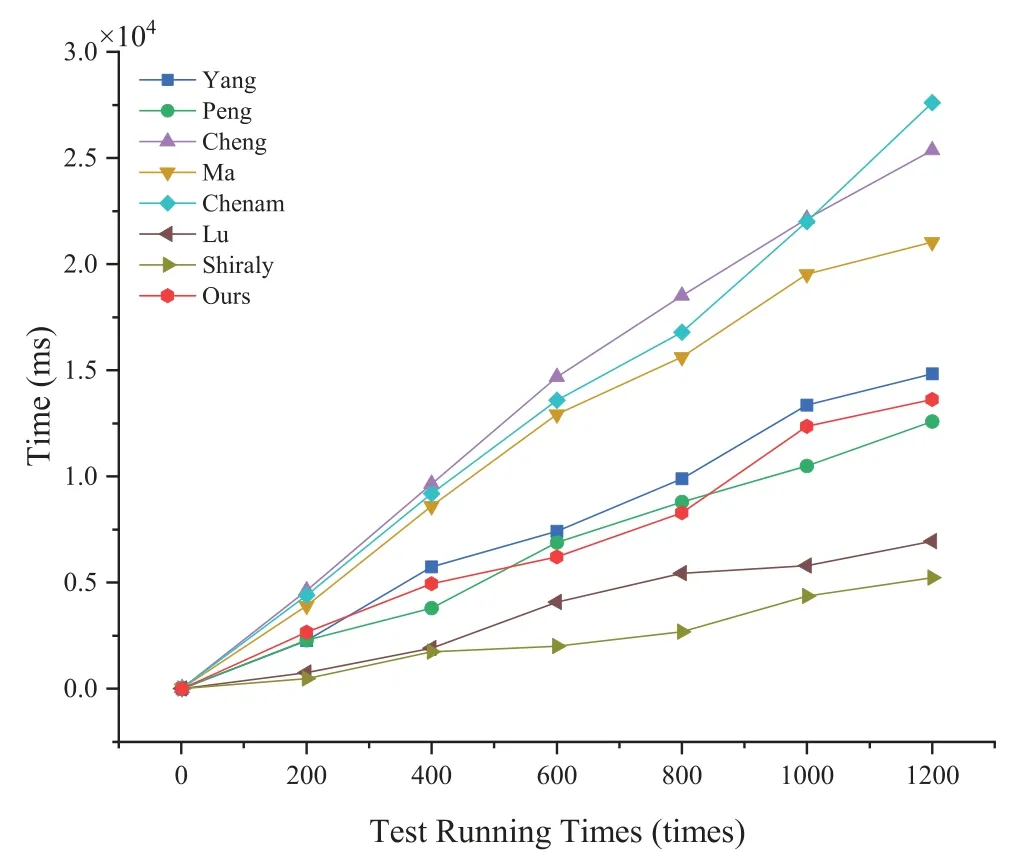
Figure 5:Running time of test
Subsequently,we make a comparison in terms of communication costs,including the size of public key |PK|,ciphertext |CT| and trapdoor |TD|,which are presented in Table 4.In the table,the notations |G1|,|G2| and |Zq| denote the bit length size for each element in G1,G2and Zq,respectively.It is clearly see that the size of ciphertext of our scheme is the same as Yang et al.’s scheme[28]and is smaller than Cheng et al.’s scheme[37],a sightly larger than other schemes;same as Yang et al.’s scheme[28],the size of trapdoor of our scheme is smaller than other schemes except Ma et al.’s scheme[4].

Table 4:The communication overhead of the schemes(bits)
Finally,we present some additional performance comparisons in the Table 5.In the table,SCF denotes designated server test,AUT denotes authenticated function,BSE denotes bidirectional searchable encryption and ASSUM denotes the difficulty assumption of the scheme security depends on.Finally,we find that our scheme is a certificateless authenticated bidirectional searchable encryption scheme with a designated server test that achieves both MCI and MTP security under the CBDH hardness assumption.

Table 5:Other performance comparison
7 Conclusion
Based on the certificateless public key authenticated encryption with keyword search (CLPAEKS) cryptosystem and the bidirectional searchable functionality,this paper proposed a new cryptographic approach named blockchain-based certificateless authenticated bidirectional searchable encryption (CL-BSE).To some extent,it can be regarded as avoiding the key escrow and certificate management problem in the PEBKS scheme,and can also be considered as appending distinctive features which allow a data owner to retrieve the keyword ciphertext from server in the CL-PAEKS cryptosystem.Taking the cloud email system as the actual application scenario,we build a concrete construction of the CL-BSE scheme.The security analysis of the scheme indicates that it can achieve both MCI-secure and MTP-secure against IKGA under the CBDH hardness assumption.
Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement:This work was supported by the National Natural Science Foundation of China(Nos.62172337,62241207)and Key Project of Gansu Natural Science Foundation(No.23JRRA685).
Author Contributions:The authors confirm contribution to the paper as follows:study conception and design:Y.Sun,X.Du;data collection:Y.Sun;analysis and interpretation of results:Y.Sun,X.Du,X.Yang;draft manuscript preparation:Y.Sun,S.Niu.All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials:The authors confirm that the data supporting the findings of this study are available within the article.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Study on the Transmission Dynamics of the Omicron Variant of COVID-19 Using Nonlinear Mathematical Models
- Novel Investigation of Stochastic Fractional Differential Equations Measles Model via the White Noise and Global Derivative Operator Depending on Mittag-Leffler Kernel
- Saddlepoint Approximation Method in Reliability Analysis:A Review
- A Review of the Tuned Mass Damper Inerter(TMDI)in Energy Harvesting and Vibration Control:Designs,Analysis and Applications
- Recent Advances on Deep Learning for Sign Language Recognition
- A Survey on Blockchain-Based Federated Learning:Categorization,Application and Analysis
