A Review of the Tuned Mass Damper Inerter(TMDI)in Energy Harvesting and Vibration Control:Designs,Analysis and Applications
2024-03-23XiaofangKangQiwenHuangZongqinWuJianjunTangXueqinJiangandShanchengLei
Xiaofang Kang ,Qiwen Huang ,Zongqin Wu ,Jianjun Tang ,Xueqin Jiang and Shancheng Lei
1School of Civil Engineering,Anhui Jianzhu University,Hefei,230601,China
2Key Laboratory of Intelligent Underground Detection Technology,Anhui Jianzhu University,Hefei,230601,China
3Chengnan College,Changsha University of Science and Technology,Changsha,410015,China
ABSTRACT Tuned mass damper inerter (TMDI) is a device that couples traditional tuned mass dampers (TMD) with an inertial device.The inertial device produces resistance proportional to the relative acceleration at its two ends through its “inertial” constant.Due to its unique mechanical properties,TMDI has received widespread attention and application in the past twenty years.As different configurations are required in different practical situations,TMDI is still active in the research on vibration control and energy harvesting in structures.This paper provides a comprehensive review of the research status of TMDI.This work first examines the generation and important vibration control characteristics of TMDI.Then,the energy harvesting performance of electromagnetic tuned mass damper inerter(EM-TMDI)is discussed.This work emphasizes the formation of a passive dynamic vibration absorber by coupling traditional TMD with inertial devices.This paper also summarizes the design and implementation of optimal vibration control and energy harvesting for TMDI.Furthermore,this paper details the applications of TMDI in the fields of bridges and building engineering.Finally,this paper summarizes the necessity of research on tuned mass-damper-inertia,the challenges faced currently,and future research directions,such as control of parameters in electromagnetic energy harvesting TMDI systems and low-cost TMDI.
KEYWORDS TMDI;EM-TMDI;energy harvesting;vibration control;inertial device
1 Introduction
Vibration control has received considerable attention in the field of engineering.The commonly used methods for vibration reduction in engineering are passive vibration reduction and isolation[1].Vibration control systems are generally classified into three types:a single vibration control system,a dual vibration control system combining two types of vibration control mechanisms,and a mixed vibration control system combining three or more vibration control systems.These systems are further classified into passive,active,or semi-active according to the provision of external energy for driving.Due to limitations in the vibration control of linear harmonic dampers,research is needed to improve the design of linear tuned mass dampers with a non-linear multi-degree-of-freedom TMDI system and energy dissipation[2].The energy collection of TMDI uses Faraday’s electromagnetic induction law to collect energy by adding electromagnetic damping.When there is relative velocity between the inertia and the electromagnetic damping,the motor will generate electricity[3–6].Currently,improvements to the tuned mass damper are divided into two categories:the selection of inertia and parallel connection.Compared to TMD,TMDI’s excellent mechanical properties allow it to play an important role in building seismic mitigation and robustness(efficiency in controlling deviations of design parameters from optimal values) [5,7,8].Although TMD has been successfully applied to suppress vibration in numerous engineering applications,the optimally designed TMDI is more effective in minimizing the response of undamped single-degree-of-freedom systems and is also a comparatively new concept[9–12].Therefore,research on TMDI has always been a very active field.
TMDI is a type of passive dynamic vibration damper that has recently been suggested for protecting buildings against seismic damage.It combines the classical TMD with an inerter,which produces resistance proportional to the relative acceleration at its two ends through its “inertial”constant.In a reasonable topology configuration,the inerter resists relative acceleration at the end and achieves mass amplification and higher modal damping than TMD[13,14].Inspired by the optimized design of TMD,Giaralis et al.[15] used a non-stationary stochastic process model to optimize the design of TMDI.Marian et al.[16] reviewed the TMD optimization design from minimizing undamped single degree of freedom (SDOF) to damping linear multi-degree of freedom (MDOF)under random base excitation in the classical TMD configuration and derived and proved the damping main structural motion control equation of TMDI under the extension of TMD.Jahangiri et al.[17] used TMDI in 2019 to ease the response of beam-type floating wind turbine (FWT) towers.Typically,electromagnetic dampers are used instead of the damping elements installed on TMDI to collect energy,namely EM-TMDI.In traditional vibration dampers such as TMD,energy-dissipating dampers are usually replaced by electromagnetic dampers(EM).The electromagnetic damper converts some of the damping energy into electrical energy,which can then provide energy source for the vibration monitoring and control system,so it can be extended to add electromagnetic damping devices to TMDI[18–21].In addition,Wang[18]proposed a geometric method to solve the challenging problem of optimizing the design of simultaneously suppressing vibration and collecting energy,while Liu et al.[21] optimized the vibration reduction and energy collection performance based on the H2 criterion.Petrini et al.[4] proposed a new optimal TMDI design formula that minimizes peak floor acceleration,providing further optimization design for energy collection TMDI configuration.Gonzalez-Buelga et al.[20] discussed the structural vibration control effect and energy collection efficiency from the perspective of nonlinear dynamics and the consideration of electromagnetic dampers and energy harvest controling (EHC) nonlinearities.This paper focuses on the design and optimization of TMDI from the perspective of nonlinear dynamics and energy conversion efficiency,which can promote the development of vibration control and energy collection in building engineering.Fig.1 is overview of TMDI’s Development and Previous Comments.
This paper is structured as follows.Section 2 begins by reviewing the development of TMDI and then introduces the basic features and principles of TMDI.In order to conduct extensive research on the TMDI,Section 3 reviews and updates the progress of vibration control and energy collection research in different fields of TMDI,analyzing and revealing the advantages of inertial components compared to mass components,and summarizing the recent research progress on electromagnetic tuned mass damper-inerter(EM-TMDI)at home and abroad.The last subsection provides a detailed review of the components of the electromagnetic tuned mass damper-inerter from the perspective of network analogies,synthesis,vibration control field,and energy collection,and discusses optimization and control methods for this device.Section 4 introduces and discusses the significance of research on electromagnetic tuned mass damper-inerter,the current challenges it faces,and the development prospects in application fields.

Figure 1:Overview of TMDI’s development and previous comments[1,3,7,9,16,18,19,21–26]
2 The Basic Theory of TMDI
2.1 The Structure of TMDI
Kawamata first introduced a liquid mass pump in 1973 that leverages fluid inertia to reduce seismic responses in structures.This is viewed as the origin of the inertial component.Inerters were first named by Smith in 2002,which are two-terminal devices that can significantly amplify physical mass by converting translational motion to rotational motion.It was not until Saito et al.used inertial elements in 2002 to enhance mass and damping of viscous damping devices that the mass amplification effect of inertial elements was recognized.Since then,the combination of inertial devices and traditional passive vibration control devices has received more and more attention.
Ikago[1]proposed a method of combining an inertial mass in 2012 with a viscous mass damper to create a tuned viscous mass damper (TVMD),which has shown better control efficiency than traditional viscous mass dampers(VMDs)and viscous dampers(VDs).Based on this,in 2013 Garrido replaced the conventional viscous damper(VD)with a tuned viscous mass damper(TVMD)in a tuned mass damper(TMD)to create a rotating inertia dual tuned mass damper(RIDTMD)[10,12].Marian et al.[16]developed a tuned mass damper inertial(TMDI)device in 2014 by parallel connecting an inertial mass with the damper and spring components of a TMD.Ruiz et al.[26,27] introduced the concept of an inertiabased dynamic vibration absorber (IDVA) in 2015,which replaced the damper element in a TMD with different configurations of an inertial mass,damper,and spring connected in series or parallel.Cao et al.[24]divided a TMDI into two serially connected TMDIs in 2019 to create a tuned serially connected TMDI system (TTMDIs).This was followed by Luo et al.in 2016,Cao et al.in 2022 for inertia-based passive control devices for foundation isolation,and Giaralis et al.in 2017,and Petrini et al.in 2020 for seismic and windinduced vibration control in high-rise buildings[28].Creatively,Brzeski et al.[29] created the tuned inertial damper (TID) in 2014 by replacing the mass element in the TMD with an inertial element.TMDI is derived from TMD,which was first proposed by Frahm for reducing the multi-degree-of-freedom(SDOF)response of a primary system with a tuned linear spring to harmonic forces within a narrow frequency[30–34].
The concept of an ideal inertial device was first proposed by Smith in 2002,and in 2004 Papageorgiou and Smith experimentally demonstrated that by incorporating a rack and pinion or ball screw mechanism,the translational energy of the structure could be converted into rotational energy stored in a relatively light rotating disc[12].Experiments by Wang et al.in 2011 and Swift et al.[17]in 2013 verified the implementation of hydraulic inertial devices with inertia values b almost independent of the mass of the physical device.The ideal inertial device can be understood as an inertial amplifying device since it acts as a“weightless”mass b when“grounded”at either of its terminals.Prompted by this consideration,tuned mass dampers-inertial systems-have been proposed which enhance the vibration control capabilities of classical tuned mass dampers.Therefore,Marian et al.[32]have demonstrated in 2013 and 2014 that utilizing the inertial amplification property can significantly improve the vibration control ability of a device under the same additional mass(thus weight)conditions(see also Fig.2)[15].
2.2 Basic Characteristics of TMDI
In 2013 and 2014,Marian et al.[13,32,35]proposed a generalization of the classical Tuned Mass Damper(TMD),which includes an“inertial”device called the Tuned Mass Damper with an Inertia device (TMDI).The TMDI introduces inertia into the conventional vibration absorber,leading to the development of various inertia-based dampers.The study of TMDI plays an important role in engineering vibration control,particularly in high-rise buildings or bridges located in areas susceptible to strong winds or earthquakes.The TMDI is an extension of the classical linear TMD,which benefits from the mass amplification effect of the inertia device,or the so-called “inertial amplification”to enhance the vibration suppression capability of the TMD [32–36].Zhang et al.[37] investigated the structural control of high-rise buildings under wind and earthquake loads and verified that under a multi-modal control mechanism concerning TMDI,it is mainly determined by the contribution of two aspects of TMDI: the damping effect associated with inertia,auxiliary mass,and damping coefficient and the negative stiffness effect associated with auxiliary mass.In the vibration reduction of tall buildings with wind excitations,the performance of the TMDI is heavily influenced by the floor to which the inerter is connected.Therefore,the vibration reduction performance of the building is calculated as a function of this parameter.It is important for designers to carefully consider the installation location of the inerter as it can significantly impact the overall effectiveness of the TMDI system.Optimal TMDI performance is achieved when the inerter end connected to the ground floor experiences zero absolute acceleration.However,connecting the inerter to a floor located beneath the pendulum mass(see Fig.3)means that TMDI can only surpass TMD if said inerter is connected to a floor at around one-third of the building’s height(see Fig.3)[38].In the most realistic scenario,TMDI exhibits significantly poorer performance compared to the classical TMD when the inerter is linked to the mass located close to the ground[38,39].

Figure 2:The tuned mass-damper-inerter(TMDI)system for multi-storey frame buildings
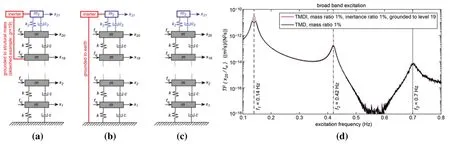
Figure 3:(a)Tuned mass damper(TMD),grounded to an arbitrary structural mass(illustrated with mass ground 19),(b)TMDI grounded directly to ground,(c)shear frame structural model with TMD,(d)transfer function of excitation force at 20th level of structural displacement
The study investigates two TMDI topologies [40].The traditional topology involves connecting the inerter in parallel with the spring and viscous damper.The nonlinear electromagnetic resonant shunt tuned mass damper-inerters(NERS-TMDI)has two different topologies.One topology involves connecting the spring,inertial damper,and viscous damper in series to increase the inertia force of the TMDI.The other topology connects these components in parallel to the stiffness of the TMDI’s mass-spring oscillator and aims to produce an additional degree of freedom.The first topology aims to increase the inertia force of TMDI,while the second aims to produce an additional degree of freedom.Results show that the TMDI with the spring,inerter,and viscous damper in series results in an increased degree of freedom of the damper while avoiding significant friction in the inerter.This benefit is realized through the series connection of the spring,inerter,and viscous damper.The use of different TMDs and inerters in base-isolated buildings results in completely different dynamic performance of the structure.Therefore,de Domenico et al.[25]proposed six different strategies for a systematic comparative study,with each strategy characterized by a specific combination of massspring-damper elements arranged in series or parallel to alleviate the displacement of base-isolated structures.The specific schematic is shown in Fig.4[41]:
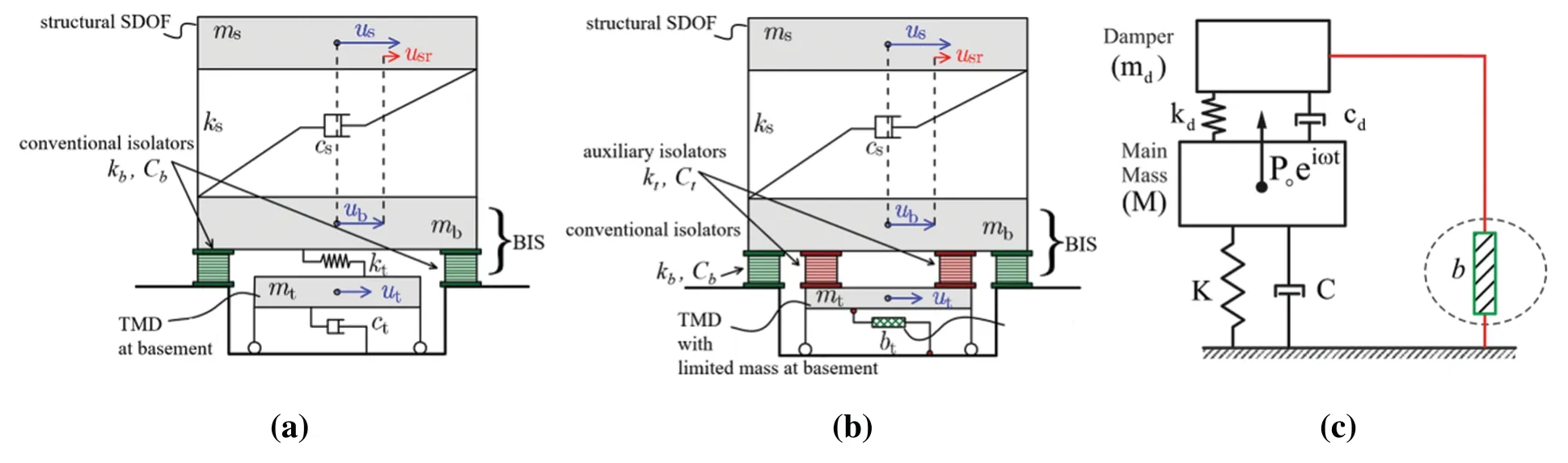
Figure 4:(a) Structural control strategy for base isolation with BIS+non-traditional TMD.(b)BIS+TMDI structural control strategy for basement seismic isolation.(c)Main concept of classical TMDI.BIS:base-isolation system
3 Design of TMDI
In recent years,the Electromagnetic Resonant Tuned Mass Damper with Inerter(E-TMDI)has received a significant amount of attention due to its ability to provide damping as well as harvest energy.This design has already been successfully applied in linear structures,but it is not yet mature in nonlinear structures.In the following,we will review the linear or nonlinear relationship and the series-parallel connection of the Electromagnetic Resonant Tuned Mass Damper with Inerter.
3.1 Vibration Control
With reference to previous indepth studies on vibration isolators,we have a preliminary understanding of the development of TMDI in vibration control [42].As shown in Fig.5 [43],Classic TMD coupled with an inerter in different TMDI topologies are proposed to suppress excessive windinduced vibrations that cause discomfort to residents in high-rise buildings[43].At the same time,it has been proposed to use two different structures for the Nonlinear Electromagnetic Resonant Series-Tuned Mass Damper with Inerter(NERS-TMDI)[44,45].Results show that NERS-TMDI is superior to existing Nonlinear Tuned Mass Dampers (NTMD) and Electromagnetic Resonant Series-Tuned Mass Damper with Inerter (ERS-TMDI) in terms of vibration control.It has been found that the first configuration of NERS-TMDI consistently performs better than the second configuration in reducing vibration and harvesting energy.The vibration behavior of ERS-TMDI system is derived when subjected to wind-induced excitation on the primary structure(see Fig.5)[5].Simultaneous,the performance of the ERS-TMDI system in vibration reduction and energy harvesting is numerically analyzed.At a high inertial ratio,research has shown that the vibration reduction performance of the primary structure deformation and relative deformation of ERS-TMDI is better.ERS-TMDI reduces the resonance peak by 35% compared to the classic TMD,and by 18% compared to ERSTMDs,significantly improving the vibration reduction effect.Finally,Luo et al.[5,22,46]introduced the combination of ERS-TMDI and single-degree-of-freedom systems,and the results showed that ERS-TMDI is superior to classic TMD,ERS-TMDs,and series-connected double-mass TMD systems in terms of structural damage protection.

Figure 5:Block mass linear models for n-storey frame buildings equipped with TMDI under wind excitation: (a) “-1”topology;(b) “-2”topology;and (c) “-3”topology.Schematic of the optimal frequency responses under different inertance ratio:(d)the deformation of the primary structure and(e)the relative deformation of the ERS-TMDI
Based on the differences between internets devices,the following Table 1 shows the available vibration control devices and their characteristics.

Table 1:Table vibration control methods and characteristics and differences between inerter in TMDI series
Since Liu et al.[53] derived the motion differential equation of the Tuned Frequency Mass Damper (TFMD) under harmonic excitation.The frequency domain displacement response of the transmission conductor acting on TMDI was analyzed using the Fourier transform.A collision-based optimization(CBO)algorithm based on heuristic algorithm was used to optimize the response of the transmission elevated-TMDI structure.Based on the CBO optimization,the transmission line TMDI system’s parameters were optimized to minimize its displacement.Through his research,he has shown that by optimizing TMDI parameters using CBO,the displacement response of the transmission line can be effectively controlled,leading to a significant improvement in vibration control efficiency.Salvi et al.introduced a new structure that simultaneously suppresses vibration and collects energy in a harmonic excitation structure based on a damped SDOF dynamic system (see Fig.6) [51].The stiffness and damping characteristics of TMD can be adjusted using a simple design formula to achieve enhanced vibration suppression (based on the peak displacement of the SDOF primary structure)and energy harvesting (based on the relative velocity at the EM terminal).This can be done at a similar resonance frequency with a fixed mass attached to TMD,as illustrated in Fig.6.Based on this situation,there exists a balance between vibration control and energy harvesting.Therefore,energy harvesting-enabled tuned mass-damper-inerter (EH-TMDI) is inspiring for future multi-objective optimization design processes.For the SDOF primary structure,the TMDI includes an inertial device connecting the additional mass of the classical TMD to the ground,as shown in Fig.6h.The mass of the classical TMD is connected to a skyhook configuration on the ground as shown in Fig.6b where β is the inertia ratio and μ is the mass ratio[51].

Figure 6:(Continued)
Due to the excellent mechanical performance of TMDI,TMDI has become an exciting candidate device in the field of passive vibration control of space-constrained offshore wind turbines.Fitzgerald et al.[54]have shown that TMDIs offer significant damping potential for floating offshore wind turbine (FOWT) towers.For the same damper mass,this new type of damper performs significantly better than a conventional TMD,and the TMDIs can significantly improve the reliability of FOWT towers in adverse weather conditions with wind and wave dislocation.The application of a passive TMDI in the vibration control of a mast-style FOWT tower was studied,and the optimal tuning parameters of the simplified fixed-base tower under white noise excitation were derived [47].The optimal TMDI design parameters were derived as a function of TMD mass and inerter constant b to minimize the relative displacement variance of the undamped SDOF structure subjected to white noise excitation[55].The findings indicate that,with a fixed TMD mass,the optimized TMDI setup is superior to the traditional TMD configuration in mitigating the displacement variance of an undamped SDOF structure when it undergoes white noise excitation.In particular,the hybrid control of the structure based on TMDI and the base-isolation subsystem under seismic excitation was studied(see Fig.7),and TMDI was optimized by implementing a simplified method based on minimizing the variance of the base isolation subsystem’s displacement (see Fig.7) [56].To increase the safety and availability of a beam structure while controlling its vibration,it has been suggested to use Lagrange’s equation in conjunction with a smart monitoring sensor for electrical grids.This approach would aid in the calculation of the response of the beam structure to seismic acceleration excitation and the corresponding displacement values,and the displacement response formula for the beam structure under kinetic force are derived[56].
where the displacement of the TMDI with respect to the base is denoted asxd(t).Letmd,b,cdandkdbe the mass,inertia,damping and stiffness of the TMDI,respectively.

Figure 7:(a)Base-isolated MDOF shear frame;(b)hybrid controlled MDOF shear frame with TMDI.Frequency response function in terms of base displacement for the hybrid controlled 20-story baseisolated structure with TLCD (black dotted line),with TMD (green dash-dotted line),with TMDI(blue solid line) and base-isolated structure (red dashed line) subjected to the 44 FEMA P-695-FF records;(c)for ζb=10%;(d)for ζb=15
The effect of the position of the TMDI in controlling wind-induced vibration of a flexible structure is investigated as shown in Fig.8,and the equations of motion for a TMDI structure system considering the inertial position are developed below [22,23,57,58].Meanwhile,based on the mass amplification effect,and control robustness conditions,the effect of inertial position on the control effectiveness,optimization of design parameters,and high-mode damping effect of TMDI is discussed[57].
whereH1andH2are the position vectors of the damping and inertial elements;andXare the acceleration,velocity,and displacement response vectors of the primary structure;M,CandKare the mass matrix,damping matrix and stiffness matrix of the primary structure.

Figure 8:Displacement response of the girder equipped with the conventional TMD or TMDI in(a)and(b).Some functions of Displacement response of the girder equipped with the conventional TMD or TMDI with error in(c)and(d)
Based on the adverse effects of crosswind vortex-induced resonance on high-rise chimneys,high-rise chimneys can be reduced to generalised SDOF structures.Based on the simulated filtered wind load spectra,analytical solutions were derived for the wind-induced vibration response of the structure with the TMDI installed.Subsequently,a parameterized analysis of the optimized design parameters of TMDI is conducted.From the basic motion equations,an analytical expression for the efficiency of TMDI wind-induced vibration response control for the generalized SDOF high-rise chimney structure is derived based on the filtered representation method.Through parameter analysis,empirical formulas for TMDI’s optimal parameters,optimal control ratio,and effective TMD mass ratio are obtained[59–61].
In the vibration control of high-rise buildings,TMDI can be used to control the structure of highrise buildings under wind and earthquake loads through the inherent multi-mode control effectiveness of TMDI.The analysis and research of TMDI’s multi-mode control effects suggest that the damping effect of the weighted difference of mode coordinates between two ends of TMDI is the main reason for the multi-mode control effectiveness of TMDI.Finally,the change trend of the equivalent damping ratio of TMDI-controlled structures under any mode is analyzed through the established model,and the design parameters that have the greatest impact on the multi-mode control effectiveness of TMDI are determined.In addition,when inertial dampers are used to reduce the wind-induced response of high-rise buildings,Studies have shown that optimally designed TMDIs or TIDs are better at suppressing wind-induced vibrations than TMDs,especially in terms of acceleration response,when assigned low or zero additional mass.Based on the concept of structural dynamics,the motion equations of the MDOF structure controlled by TMDI can be expressed in a matrix-vector[13]:
whereM,C,andKare the mass matrix,viscous damping matrix,and stiffness matrix of the primary structure,respectively.denote the corresponding velocity and acceleration response vectors.p(t)denotes the excitation vector acting on each degree of freedom at a moment.
The generalized SDOF system is only suitable for the design of TMDS and inter-floor TMDIs adjusted to the basic vibration mode.For TMD-Nonconventional (TMDNC) and TMDI tuned to higher modes or with a multi-level topology structure,a generalized MDOF model(see Fig.9a)can be used for more reliable vibration control performance evaluation and parameterized design.Fig.9b lists the performance influencing factors of TMDI.
In order to combine the optimization of TMDI tuning with the design of the main structure to improve performance under dynamic loads,the influence of the elastic and mass characteristics of the main structure on the performance of TMDI motion control is investigated,an innovative parameter study can be conducted.This relates to various tapered beam-like cantilever main structures which produce continuously varying bending stiffnesses and mass distributions[13,62–65].
3.2 Energy Harvesting
By combining an inertial damper with Tuned Mass-Damper,an inertial-based TMD was obtained,and the closed-form displacement equations and power equations of generic tuned massdamper-inerter (GTMDI) were derived [52].The working mechanism of GTMDI was revealed and elucidated,and it was confirmed that GTMDI has dual benefits,namely reduced input energy and enhanced dissipation power effect.Fig.10 is a schematic diagram of the coupling between the mechanical and motor network systems in the TMDI system.
Studies have found that adding electromagnetic motors to TMDIs with different damping characteristics can increase the available energy of wind-induced high-rise buildings[4].In TMDI topologies where inertial units cover more floors,the acceleration of the floors can be simultaneously reduced while increasing the available energy.Theoretical studies have been conducted on the performance of non-linear shape memory alloy (SMA) springs in inertial devices for controlling wind-induced vibrations in high-rise buildings[6].The potential for energy harvesting using this temporary passive control device was also investigated.

Figure 10:Schematic diagram of mechanical and motor network system coupling in TMDI system
From the perspective of frequency domain analysis,compared to traditional TMDs,classical TMDs only tune the mechanical damper,while ERS-TMDI can improve vibration control and energy harvesting performance by tuning the resonance of mechanical dampers,inertial units,and electromagnetic resonators [5].Therefore,ERS-TMDI can efficiently harvest energy and improve energy harvesting efficiency (see Fig.11).Fig.11a shows a typical generated fluctuating wind time history with a duration of 100 s and a time interval of 1 s.In Fig.11b,the wind time history produced is compared to the Davenport spectrum by inverse fast fourier transform(IFFT)for power spectral density.It is clear from Fig.11 that both classical TMD and ERS-TMDI have displacement damping effect at the same time and their relative reduction rates are 9.71%and 11.49%.In this case,the peak displacement of the primary structure of ERS-TMDI is reduced by about 9.78%,while the relative reduction rate in terms of acceleration is 6.95%[5].
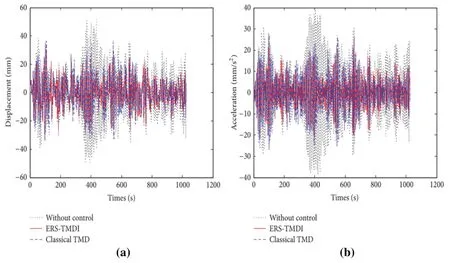
Figure 11:Time-history responses of(a)displacements and(b)accelerations of the primary structure:comparison between classical TMD and ERS-TMDI
Luo et al.[5] introduced the standard performance of ERS-TMDI by comparing it to classical TMD,ERS-TMDs,and Series Dual Mass TMDs (SDM-TMDs),in order to achieve minimum structural damage and energy harvesting under stochastic wind excitation.As shown in Fig.12b,Petrini et al.[50] studied the potential of coupling TMDs with inertial devices in different TMDI topologies to dissipate the vibration due to crosswind vortex forces in high-rise buildings while generating electric energy.When a renewable electromagnetic motor(EM)is connected to the TMDI,the damping characteristics of TMDI will be allowed to change,and part of the kinetic energy dissipation will be converted into electrical energy.The results (see Fig.12a) show that the energy available for collection can be increased by increasing the damping of the TMDI beyond the optimum value for vibration suppression,or by sacrificing greater bottom plate acceleration at the expense of reducing the inertial characteristics.

Figure 12:Sensitivity of the DV optimum to changes in wind speed at u=0.5%in(a)Connection of the EH-TMDI system in presence of an EM in(b)
Since the optimal stiffness and damping characteristics do not significantly change with the reference wind intensity used in the design and evaluation of high-rise buildings for occupant comfort and accessibility,the potential for TMDI to simultaneously perform energy harvesting and vibration suppression has been quantified by coupling TMDI with regenerative electromagnetic motors,allowing for changes in optimal TMDI damping and inertia.Therefore,in wind-induced high-rise buildings,with regard to the power generation control of sensors and actuators for health monitoring and climate control in modern structures,this can be increased by considering the occupancy situation or relaxing the availability limit state thresholds for floor acceleration to meet the comfort of the occupants.
The considered TMDI configuration is suitable for controlling the dominant vibration mode of a vertical cantilever structure[66].Based on this,an analytical model of a cantilevered flexural structure with an electromagnetic pulse as an ideal damper for TMDI is established.The main structure is considered as a generalized single-degree-of-freedom structure with mass and stiffness characteristics depending on the first vibrational mode.The analysis results show that under stationary white noise excitation,the further distance between the inertia mass and the top of the main structure,the better.
A large body of research has shown that ERS-TMDI has gained broad attention in the field of vibration mitigation and energy harvesting (see Fig.13).Although this design is well established in linear structures,it has not been widely applied in nonlinear structures[44].The significance of this work lies in the use of only a single device to achieve vibration suppression and energy harvesting of non-linear vibrating structures.The experimental results show that the proposed NERS-TMDI structure performs better than the existing non-linear tuned mass dampers(NTMD)and ERS-TMDI in terms of vibration control (see Fig.13).The results also show that the first configuration of the NERS-TMDI always outperforms the second configuration of the NERS-TMDI in terms of vibration control and energy harvesting.However,the stability and bifurcation analysis of the NERS-TMDI remains to be investigated and future work will involve the development of suitable optimization schemes to improve the existing design options for the NERS-TMDI[48,49].

Figure 13:Schematic representation of the primary mass connection to the NERS-TMDI for(a) configuration-1 and for (b) configuration-2.Energy collected in NERS-TMDI configuration-1 against the inerter magnitude and the impulse magnitude: (c) three-dimensional graph and(d)contour plot.The parameters for the primary system are ms=1 kg,ks=1 N/m,ksn=1 N/m3 and cs=0.002 Ns/m
The electromagnetic tuned mass-inerter damper (EM-TMID),proposed by Luo et al.[67],achieves the dual functions of vibration suppression and energy harvesting.A new feature of this damper is that it replaces the viscous damping of the traditional TMD with an inertial electromagnetic transducer.Based on the Alembert principle,a dynamic model of the EM-TMID and a single-degreeof-freedom structure under earthquake excitation was established.Using the H2 norm method with the minimum root-mean-square damage value of the primary structure as the objective,the EM-TMID was optimized by considering both frequency domain and time domain numerical simulations,and the dual functions of vibration suppression and energy harvesting were analyzed.The results show that EM-TMID outperforms classical TMD,EM-TMD and TMDI in reducing the peak and area of the frequency response of the primary structure displacement in the frequency domain;while EM-TMID outperforms classical TMD in reducing the peak and root mean square values of the displacement and acceleration in the time domain.The mechanical model of the EM-TMID-single-degree-of-freedom structure coupling system can be established based on the D’Alembert principle as follows:
wherekv,kfare the electromagnetic sensor constants,ideallykv=kf;R is the resistance,R=Ri+Re;kTis the stiffness of the TMD;mTis the mass of the TMD;bis the inertia mass;xTis the displacement of the TMD;xsis the displacement of the main structure;andLis the electric current.
The traditional TMD is connected to the ground via an inertial device.The inertial electromagnetic transducer and its related circuitry replace the viscous damping of the classical TMD.The transducer is assumed to be an ideal transducer that is parallel to a resistor,an inductor,and a capacitor(RLC)circuit made up of resistance,inductance,and capacitance.Two types of RLC circuit structures were studied:one is in series and the other is in parallel.The equations of motion for the system are given as follows[3]:
wherekvis the transducer voltage constant.kfis the force constant of the transducer.
Fig.14a is the representations of structures.The objective of ERS-TMDI is to simultaneously suppress unnecessary vibration and collect energy from vibrating structures (see Fig.14b).The Matlab optimization toolbox was used to numerically verify the optimal expression obtained (see Fig.14c).The results showed good consistency between the two.These optimal parameters,namely the electromagnetic-mechanical coupling coefficient,were found to be dependent on the mass ratio and inertia ratio.Through parameterized studies,the effects of the mass ratio and inertia ratio on the optimized design parameters were examined.The results showed that an increase in the mass ratio and inertia ratio can improve the electromagnetic-mechanical coupling coefficient and damping ratio,and it was also found that the parallel RLC structure(see Fig.14b)is superior to the series RLC structure in energy harvesting and has similar performance in vibration suppression[3,67].
In conclusion,it can be seen that all studies on TMDI in the context of energy harvesting clearly demonstrate that the proposed inertial device is feasible and useful in controlling wind-induced vibration of buildings and converting dissipating energy into electrical energy.

Figure 14:Representations of structures in (a).(b) shows the schematic structure of the main unit with ERS-TMDI absorber,divided into series and parallel circuits.Three-dimensional representation of performance index (PI) with respect to electromagnetic mechanical coupling coefficient μk and electrical damping ratio εe under μ=0.02,δ=0.1,ft=1.018,and fe=0.981 in(c)
3.3 Optimization and Design
Bian et al.[68] studied design,optimization,and evaluation techniques for TMDI used on circular cross-sectional structural components.Zero-mean white noise random processes were used as external excitation loads.Two design objectives were to minimize the variance of the primary structure’s displacement and to maximize the energy dissipation index(EDI)as a method of selecting the optimal design parameters.Lara-Valencia et al.[69]discussed the optimization design of TMDI using exhaustive search and demonstrated that linear combination optimization design schemes are valuable and easy-to-implement tools.It was suggested that as research and practical applications of TMDI devices continue to develop,nonlinear analysis should be the focus of future developments in this field.Masnata et al.[70]proposed a new type of TMDI,which incorporated a recently developed Non-Traditional Tuned Mass Damper(referred to as new TMD)in combination with a base-isolation(BI) system to control the displacement of a base-isolated structure under earthquake action (see Fig.15).The new TMD consisted of a secondary mass system connected to the BI system’s baseplate via a spring and connected to the ground via a damper,as well as an inertial device parallel to the damper,as shown in the figure below.Ye et al.[71]used simplified 3DOF and MDOF structural models to evaluate the effectiveness of a double-isolation system with optimal supplementary disturbance sources by using artificial and actual seismic records for time-lapse analysis.The results show that the maximum absolute floor acceleration of the dual isolation system (DIS)-inerter-MDOF-1 model is significantly lower than that of the base-isolated structure of multi-degree-of-freedom(BIS-MDOF)-MDOF model,but slightly higher than that of the original double-isolated system.

Figure 15:Base isolated structures: (a) MDOF base isolated shear-type frame;(b) MDOF baseisolated TMDI-controlled shear-type frame;(c) MDOF base-isolated New TMDI-controlled sheartype frame;(d)Sketch of a single-storey building containing a tuned mass damper(TMDI)with SDOF base isolation
This device is connected to the baseplate of the isolated structure via a spring and a damper in the traditional form of TMD.Some studies have shown that it can effectively reduce the displacement of the base-isolation sub-system and the primary structure[24,25].This novel design includes a TMDI with the damping element directly connected to the ground.The results show that under the same mass ratio,compared to the classic TMDI,the new TMDI can better reduce the displacement of its substrate isolation subsystem even further[26–28].
Pietrosanti et al.[65] presented an optimization technique for designing TMDI for MDOF structures.By analyzing the influence of the mass ratio and comparing its performance with that of TMD with the same mass,it was found that using an inerter is particularly suitable when using a small amount of auxiliary mass.The optimization design of TMDI was investigated by di Matteo,who proposed a numerical method to directly optimize the TMDI under white noise excitation.This was done to control the acceleration response of a base-isolated structure.A.Giaralis established a design framework for earthquake-excited TMDI-assembly-layer buildings,considering mass amplification effects,using inertia as a design parameter,and considering the stiffness and damping characteristics of TMDI.By ensuring that the contribution of all structural modes to the design objective function evaluation is explicitly taken into account,optimal design is achieved across the entire frequency range [70,72,73].It was found that compared with the same mass TMD,when the TMD mass and TMDI topology structure are smaller (where the inerter connects the TMD mass to the following two layers),including the inerter achieves enhanced performance improvement,and TMDI has quite robust properties,with limited influence of excitation characteristics on actual optimization design[74–76].
Djerouni et al.[77] developed a mathematical model for TMDI in building seismic mitigation using MATLAB Simulink,which demonstrated the robustness,performance,and effectiveness of TMDI.de Domenico et al.[78] found the optimal parameters for TMDI based on probability framework and investigated different optimization algorithms (see Fig.15d).The effectiveness of the optimal TMDI parameters was evaluated through time history analysis of multi-story isolated structure under multiple earthquake excitations.Three distinct methods for optimizing TMDI were developed using white noise as the fundamental excitation.The efficiency of designing and assessing TMDI systems based on earthquake excitation was also explored[1].The results showed that TMDI could effectively reduce the dynamic response of the system,and the use of inertial systems could achieve lightweight of the system,with better performance and robustness than classical systems.Two kinds of nonlinear constitutive behaviors were considered,and a dynamic layout scheme was proposed in which TMDI was installed below the isolation layer of the foundation isolation structure to improve the seismic capacity and reduce the displacement demand of the isolation structure[79].Patsialis et al.[12]established a reduced order model(ROM)on the basis of the original finite element model.However,Kaveh et al.[41]computed the optimal parameters for the free vibration of TMDI with single and double inertias arranged at various positions in the optimization design of both SDOF and MDOF models(refer to Fig.16).These parameters include the natural frequency and damping ratio.The results showed that the tuned dampers with rational configurations had better performance than the classical TMDs with the same weight(mass).

Figure 16:Single degree of freedom(SDOF)primary structure with TMDI coupling
Firstly,a case study was conducted to apply the inertia dampers to adjacent high-rise buildings.Secondly,a multi-objective evolutionary algorithm,i.e.,non-dominated sorting genetic algorithm,was used to solve the quality-constrained optimization problem of multi-tuned mass damper inerter(MTMDI)parameter[9,80].Finally,a comparison was conducted among MTMD,single TMDI,and MTMDI systems that consist of TMDI and TID while considering practical design considerations that are related to using realistic and feasible constraints for maximum mass ratio.de Domenico proposed a TMDI-enhanced foundation isolation system mounted on an isolation floor[78,25].The effectiveness of the optimal TMDI parameters was evaluated through time history analysis of multistory isolated structure under multiple earthquake excitations.By applying D’Alembert’s principle,the motion control equation of a three-dimensional system can be easily expressed in matrix form[78]:
where g(t)is the horizontal ground acceleration to which the combined system is subjected.
Pietrosanti et al.[81]presented an optimization design method for TMDI based on multi-degreeof-freedom structures.The study examined MDOF structures with ground-connected or unconnected TMDIs and proposed a method for a generalized two-degree-of-freedom model suitable for optimizing control system design.Under the basic acceleration with only the horizontal translational component of motion considered at each level,the motion equations for such a structure can be expressed as follows[81]:
whereM,L,andKare the mass,damping,and stiffness matrices,respectively,uis the horizontal displacement vector with respect to the ground,uTis the relative displacement of the massmTwith respect to the ground,anduj,ukare the relative displacements of thejandKdegrees of freedom with respect to the ground,respectively.τis the unit vector,fBis the interfering force acting on k-dof,andfTis the viscoelastic force acting on j-dof,and finallyBkandBjare the assigned vectors.
A comparison between traditional passive TMD and TMDI was made,and the building was modeled mathematically with MATLAB Simulink [1].The simulation results demonstrated the effectiveness,robustness,and performance of the method.In addition,a new structure called Tuned Mass-Damper Inertial Resonator(TMDIR)was proposed to suppress ground motion,such as base or excitation force.Liu et al.[82]investigated the vibration control and optimization design problems of the Tuned Mass-Damper Inertial Transmission Line(TMDITL)and they developed the differential motion equation for TMDI transmission line under harmonic excitation and utilized frequency domain analysis to obtain a closed-form solution for the displacement response spectrum of the transmission line.The design parameters of TMDI were optimized using fixed point theory and the researchers discussed the vibration control performance of TMDI based on this optimization.
A dynamic layout scheme was proposed in which TMDI was installed below the isolation layer of the foundation isolation structure to improve the seismic capacity and reduce the displacement demand of the isolation structure[79,83].Matteo et al.[74,84]studied the response of the foundation isolation structure controlled by TMDI under stochastic horizontal base acceleration.Firstly,a direct numerical method was proposed to optimize the device under white noise excitation,and a simplified analytical solution for TMDI parameter optimization design of foundation isolation structure was further proposed.Under this method optimization,the response of the foundation isolation structure under strong earthquake excitation can be effectively reduced.Bian et al.[85] proposed a hybrid vibration control method BI-TMDI for the vibration suppression of substation systems.A theoretical optimization model of the switches mounted on frame (SMF)-BI-TMDI system based on a threedegree-of-freedom analogy was developed,which can be used to explicitly consider the interactions between the switch,base isolation frame and TMDI.The results of the time course analysis of the SMF-BI-TMDI system under the action of a strong seismic ground motion ensemble validate the effectiveness of the BI-TMDI vibration control method as a promising vibration control method that can be used to improve the seismic response of the substation and its components.
The article introduced a calculation method for structural damage under stochastic ground acceleration excitation and compared it with the ERS-TMDs,TMDI,and TMD,as shown in Fig.17 of the article referenced by citation [86].The article mentioned that closed-form solutions were obtained,which included the optimal mechanical tuning ratio,optimal electrical damping ratio,optimal electrical tuning ratio,and optimal electro-magnetic-mechanical coupling coefficient.Fig.17d in the article illustrated the optimal performance indicators for earthquake control.
Petrini et al.[4,87] proposed a new scheme for the optimization design problem of TMDI to determine the damping and stiffness characteristics of TMDI.This approach can minimize the key floor acceleration for building occupants in cross-wind direction using the previously designed TMDI inertia characteristics and topology structure(see Fig.18a).Through extensive inertia characteristics and three different topology structures,optimized TMDIs were obtained(see Fig.18b).

Figure 18:(a) A wind-driven case of a typical rack-and-pinion flywheel inerting device with a“–p”TMDI topology and n gears was used to study a block mass surrogate planar frame model of the building.(b) Peak top floor acceleration achieved with optimally designed TMDIs in different topologies and inertial properties:Secondary mass ratio μ and inertance ratio β
Three distinct optimization techniques were introduced for TMDI,utilizing a zero-mean white noise random process as the primary stimulus.A MTMDI system (consisting of multiple TMDIs)was used as an unconventional seismic protection strategy to connect two adjacent high-rise buildings[1].Using NSGA-II for displacement-,inter-story drift-,and acceleration-oriented optimization,four optimal parameters for each TMDI in the MTMDI system,namely,mass ratio,inertia ratio,frequency ratio,and damping ratio were obtained[88].Two inertia-based isolation systems(see Fig.19),namely,the inertial damper (ID)-based isolation system,in which an isolation system based on a parallel connection of an ID and a viscous damper,as well as a series connection of an inertial damper,a spring damper,were put forward.The former is referred to as a TID-based isolation system[89].Based on the optimal damping ratio and inertia ratio,both ID-based and TID-based isolation systems can reduce relative displacement,absolute acceleration,and base displacement.The results showed that ID-based and TID-based isolations have great prospects in the application of base isolation.A seismic hazard model was developed by Patsialis et al.[12]using a representative set of acceleration time course models to investigate the implementation of TMD and TID as limit cases for TMDI.The results show that both TID and TMDI achieve almost identical performance throughout the front end,for both linear and non-linear structures.When the inerter vibration absorber(IVA)is placed at a lower floor level,improved vibration control efficiency is achieved for both linear and non-linear structures,and better vibration suppression is achieved by allowing the IVA to span two floors.A novel design formula for a TMDI system was proposed in order to address the discomfort experienced by residents in tall and slim high-rise buildings that are susceptible to vortex shedding effects.Furthermore,the potential for converting wind-induced energy into usable electricity for these buildings was explored using this optimal TMDI design[19,90,91].
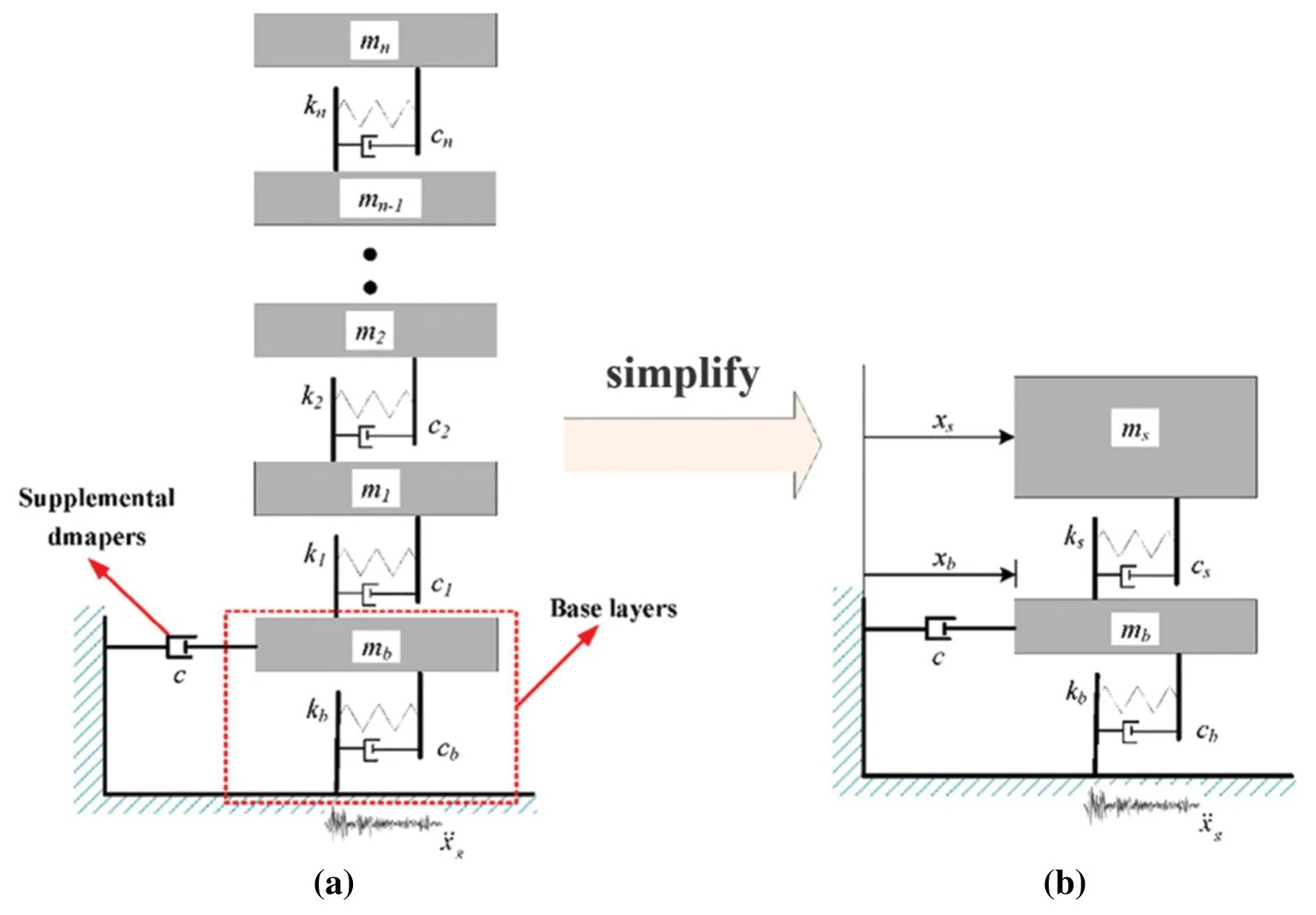
Figure 19:The simplified model of the superstructure: (a) a MDOF building with a base isolation system;(b)the simplified SDOF structure with a traditional base isolation system
The majority of the research on TMDI systems has centered around optimizing tuning methods and connection arrangements to enhance the motion control efficacy of specific primary structures.Domenico and colleagues also investigated the impact that the elastic and mass properties of the primary structure have on the motion control performance of TMDI systems (see Fig.20).The innovative parameter study conducted by Domenico and his team involved a vast array of conical beam-like cantilever primary structures,enabling the exploration of the combination of optimal TMDI tuning with primary structure design to enhance dynamic load performance.This represents a significant step forward in the field of TMDI systems research.
The advantages and disadvantages of the existing optimization methods are summarized and the following Table 2 shows the optimization methods for TMDI.

Table 2:Advantages and disadvantages of TMDI optimization methods
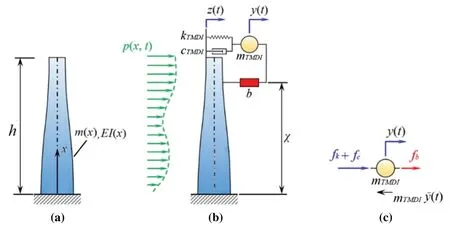
Figure 20:(a)Continuous flexural cantilevered uncontrolled(primary)structure,(b)TMDI-controlled structure,and(c)external loads acting on the TMDI mass[23]
4 Application of TMDI in Energy Collection and Vibration Control
4.1 Vibration Control and Energy Collection of High-Rise Buildings in Wind and Earthquake Conditions
According to Zhu’s analysis,the transfer functions of displacement and acceleration responses suggest that TMDI is more efficient than TMD in reducing wind-induced responses of coupled highrise buildings.This is true even when the mass of TMDI is one-third smaller than that of TMD.Application of TMDI to wind vibration control in coupled high-rise buildings.This would be a good solution to the wind vibration control problem in coupled high-rise buildings.In the following discussion and research,we will focus on the relevant hot issues of TMDI in the field of high-rise buildings.
4.1.1 Vibration Optimization of TMDI under Known Risks in High-Rise Buildings
Due to the additional inertial mass provided by the inclusion of an inertial device,TMDI is more effective than TMD in reducing the vibration of high-rise buildings caused by earthquakes.Petrini et al.[4]mentioned that by spanning more floors with the inertial device,TMDI is more robust to perturbations in structural properties than TMDs.
Ruiz et al.[11] considered the system’s lifecycle cost,the probability of exceeding it during the construction lifecycle,and performance criteria with respect to the inertial size and the actual constraint of the structural connection.In these aspects,the optimal configuration of TMDI can achieve a reduction in both the lifecycle and building maintenance costs,at the expense of an increase in the inertial force.For a high-rise building,the initial equipment cost is primarily related to the mass of TMDI,while the other two criteria correspond to the maintenance cost and the design of the inertial force corresponding to the inertial device.In the description of risk and quantitative design indicators,Ruiz adopts a probabilistic seismic wind risk quantification framework and design variables(see Fig.21a).
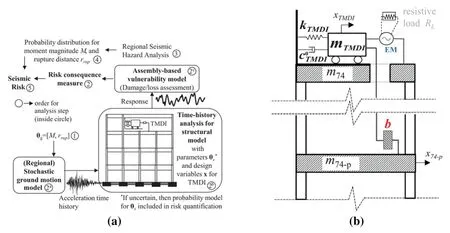
Figure 21:(a) Proposed energy harvesting enabled TMDI for energy generation in wind-excited tall buildings.(b)Overview of risk quantification and assessment approach
Furthermore,under the same inertial coefficient and additional mass ratio,installing the inertial device at lower floors has played a significant role in all performance criteria examined,as the inertial device operates more efficiently[33,94].Li et al.[95]mentioned in the paper the strong characteristics of TMDI with respect to the main structural features and reference wind speed,which can be increased by adding inertial mass blocks or by increasing the inertial connection secondary mass to span more floors of the high-rise building.Qiao et al.[13]proposed a concept based on the structural dynamics,representing the matrix-vector form of the motion equations of multi-degree-of-freedom structures controlled by TMDI[13]:
whereM,C,andKare the mass matrix,viscous damping matrix,and stiffness matrix of the primary structure,respectively.Vectorx(t)is the relative displacement of each degree of freedom of the main structure at any time t.represent velocity and acceleration response vectors.
Two representative excitations are wind load and seismic input[13]:
wherep(t)denotes the excitation vector acting on each degree of freedom at moment t.whereJis the influence vector.ugis the horizontal acceleration of the seismic ground motion at moment t.
The control forces generated at both ends of the TMDI system acting on the degrees of freedom attached to its upper and lower ends can be calculated as[13]:
wherexa,xi,andyare the displacements of the ground-relatedathDOF,ithDOF,and auxiliary mass,respectively.
4.1.2 Energy Collection Optimization of TMDI for High Rise Buildings under Wind Excitation and Earthquake Response
Previous research has shown that TMDI can effectively control vibrations in a range of different structures under various dynamic excitations from external environments.The main structure can be connected to the TMD mass by replacing the viscous dampers with electromagnetic motors (EMs)along with energy harvesting or storage circuits[18–21].By utilizing this method,instead of dissipating as heat in the dampers,a portion of the kinetic energy from the main structure is transformed into electric power that can be utilized.The resulting energy can be stored in batteries for future use.
Adding electromagnetic generators to TMDI with different damping characteristics can increase the available energy in wind-excited high-rise buildings.Qiao et al.[13,92] showed in their research on the H2 and H∞norm estimates of the displacement frequency response of structures controlled by conventional TMD (TMDC),non-conventional (high mass ratio) TMD (TMDNC),inter-story TMDI,and multi-layer topology TMDI that the generalized SDOF system is only applicable to the design of TMDC and inter-story TMDI tuned to the fundamental vibration mode.For TMDNC and TMDI tuned to higher modes or with multi-layer topology structures,it is recommended to use a generalized MDOF model(see Fig.7a)to obtain more reliable vibration control performance evaluation and parameterized design.
Petrini et al.[4]mentioned in their research that TMDI topology with inertial units spanning more floors can simultaneously reduce floor acceleration and increase available energy.Petrini extended the TMDI configuration,which initially harvested energy from harmonic-based excitations in SDOF structures,to include wind-induced vibrations in tall buildings.In this regard,this paper proposes a new optimal TMDI design formula that minimizes the peak acceleration on the top floor.The formula quantifies the optimal performance of high-rise buildings in terms of connectivity and TMDI properties (i.e.,attachment mass and inertia) as a function of the comfort of residents,through numerical solutions.It further provides a new EH-TMDI configuration optimized design under the performance standards mentioned above and demonstrates the increase in available energy by considering TMDI configurations with inertial units spanning more than one floor and allowing for changes in damping and inertial properties.Fig.21b shows energy harvesting with TMDIs with different inertia and electromagnetic damping properties:
In the process of energy harvesting,the electromagnetic component can function as a damping device,dissipating a portion of the building’s vibrational energy while simultaneously converting another portion into electrical energy,and the damping coefficient in TMDI can be changed through the characteristics of the electromagnetic circuit to achieve passive-adaptive mode changes.However,balancing the relationship between vibration control and motor energy harvesting by changing the damping characteristics needs to be combined with actual situations.The more floors the inertial device spans,the more beneficial it is for vibration control to improve the comfort of residents while harvesting energy in wind-excited high-rise buildings.Djerouni et al.[96]used genetic algorithms to optimize the TMDIs for each earthquake motion and studied the dependence of optimal parameters for control schemes on seismic motion characteristics.Due to the lower damping ratio of the control device,TMDIs perform better in controlling responses to near-fault ground.Therefore,to maintain the control device’s displacement within a practical and acceptable range,it is favorable to minimize the damping ratio.Caicedo et al.[97] presented a method for adjusting TMD and TMDI located on the upper floors of high-rise buildings under seismic excitation.The calculation of design parameters used a new metaheuristic method based on a differential evolution approach [62] and a timedomain elastic time-history analysis,where the analysis of three strategic parameters involves using objective functions such as minimizing peak displacement,minimizing Root-Mean-Square (RMS)displacement response,and minimizing peak bottom acceleration of horizontal displacement.Finally,the results suggest that displacement has an obvious amplification trend as the inertial value increases.
4.2 Vibration Control and Optimization Design of TMDI in Long Span Bridges
Research on vibration control of bridges under the condition of non-ideal vortex-induced vibration based on inertial conditions is quite limited in actual large-span bridge engineering.Since Jin et al.first proposed using Inerter-based dynamic vibration absorbers (IDVAs) to reduce bridge vibration under harmonic excitation in 2016,Dai et al.[98]mentioned that under the same mass ratio,IDVA is more efficient than traditional TMD.Xu et al.later proposed using TMDI to suppress vortexinduced vibration of bridges in 2019 (see Fig.22b).Since the inertial body of TMDI has an inertia force,which is equal to adding a virtual mass on the basis of the vibration mass block of the original TMD,TMDI has an excellent effect on the seismic control of bridges.
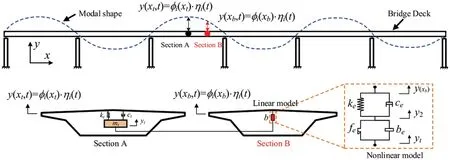
Figure 22:Schematic diagram of the bridge-TMDI system
In recent years,the research conducted by Dai et al.in 2019 focused on the effect of inertial span on TMDI control efficiency,while Xu et al.compared different IDVA layouts and their effects on vortex-induced vibration(VIV)control in large-span bridges in 2020.Dai et al.utilized the Maxwell element to replace the damping element in TMDI in 2021 for VIV control in bridges.However,these are only theoretical studies based on TMDI.In this article,we will summarize the implementation and optimization of vibration control using TMDI in large-span bridges[99].The schematic diagram of the TMDI system in bridge construction is shown in Fig.22 below[95].
4.2.1 Vibration Control Design of TMDI in Bridges
After the large-span bridge is put into use,the actual environment such as wind,earthquakes,and passing vehicles and pedestrians will seriously affect the fatigue life and performance of the bridge structure.Due to the continuous increase in span,the bridge structure is becoming more and more complex and flexible,and is therefore frequently affected by wind.Non-ideal VIV can significantly impact both the fatigue life and performance of large-span bridge structures,resulting in damage to crucial components and even leading to collapse.Therefore,it is crucial to take measures to suppress VIV in large-span bridges [99].The TMDI system can significantly reduce the VIV response of the bridge deck.Compared with the traditional TMD system,the TMDI system has significantly reduced static tension caused by gravity in the spring and oscillation amplitude of the mass block.These features make the proposed TMDI system an attractive alternative for VIV control of large-span bridges.Fig.23a shows the structure of TMDI under SDOF[100].
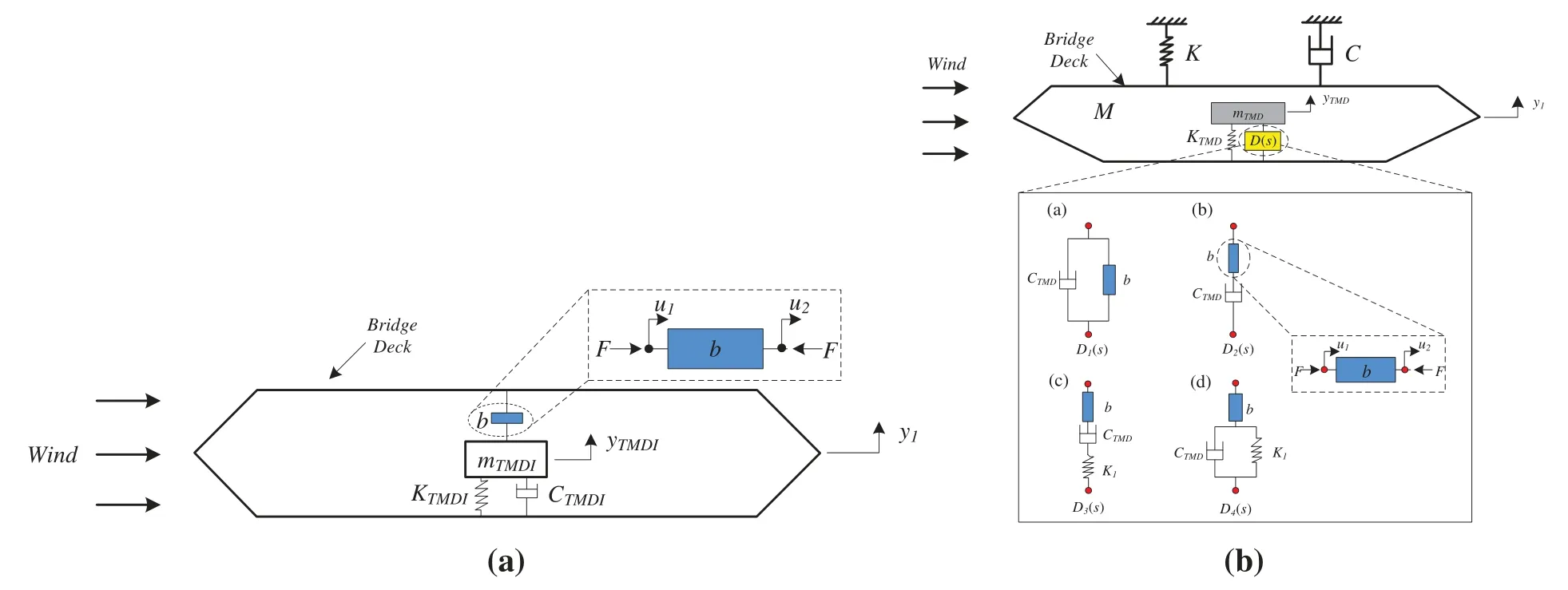
Figure 23:(a) Single-degree-of-freedom primary structure incorporating with a TMDI system.(b)Schematic diagram of the bridge–IBD system.IBD,inerter-based damper[7]
In fact,different combinations of inertial dampers,springs,and dampers can produce varying results.Among so many combinations,there are almost no applications of IBD to control windinduced vibration in engineering structures.Giaralis and Petrini first attempted to apply IBD to wind-induced vibration control of civil structures.Xu et al.[7] studied the effectiveness of different combinations of IBD on VIV control of large-span bridges and proved that IBD or TMDI plays a good role in reducing earthquake-induced vibrations and controlling other vibrations of civil structures.Fig.23b shows the schematic diagram of the bridging-IBD system.
Excessive out-of-phase vibration between adjacent components can also cause damage to the bridge.Song et al.[93]proposed using a TID system to reduce the impact and instability damage that may occur in adjacent bridge structures under strong earthquake action.By using optimization design with fixed points,it was found that compared with the classic TMD system,the proposed TMDI system has better dynamic response reduction performance and the inertial element can significant improve the isolation performance.Palacios-Quiñonero et al.[101] studied the modal characteristics and dynamic response of a two-degree-of-freedom system,while Basili et al.[102] proposed using TMDI system for seismic protection of adjacent buildings.Palacios-Quiñonero et al.[103]implemented the MTMDI system to link two high-rise buildings and assessed its control efficacy based on both displacement and acceleration measurements.Basili et al.[8–10] integrated soilstructure interaction (SSI) effects into the examination of neighboring buildings connected with spring-dashpot-inerter elements (SDIE) in parallel formation and optimized design parameters to achieve a pre-established displacement target.Palacios-Quiñonero et al.[101] employed a tuned liquid column damper(TLCD)to lessen the seismic response of neighboring tall buildings.Palacios-Quiñonero et al.[103] investigated the seismic response of two adjacent towers that were equipped with visco-inertia mass dampers(VIMDs).These studies show that although the application of inertial agents in adjacent structure vibration control is relatively less than that of controlling the vibration of a single engineering structure,Song’s et al.[93]research has shown that the relative response between adjacent structures in different structural systems will have a great impact on the seismic performance of the TMDI control system.
4.2.2 Optimization Design of TMDI in Bridge Applications
TMDI,as a common vibration control method,has been widely used in practical engineering.However,there are still technical challenges in the optimal design process of TMDI.Because the vibration problem of bridges has an important impact on the structural performance and safety,tuned mass damper installation has been widely used in bridge structures as an effective bridge vibration control technique.However,in practical applications,various factors,such as external environmental loading,multimodal vibration,etc.,need to be considered in order to select the optimal TMDI design solution to control the bridge vibration [104,105].For example,due to the flexibility of large-span bridges,it is challenging to limit the stroke of the TMD.However,TMDI has the characteristic of negative stiffness,which can effectively solve the main problem of mass dampers in flexible bridges[106–108].
The advantage of TMDI in vibration control mainly comes from the“mass amplification effect”generated by the inertial body.This inertia can exert a certain damping effect,thereby optimizing vibration suppression for different modes by comparing the frequency response function and the same as dynamic transfer function of the main structure.Feng et al.[109] showed that the use of IBDs including TMDI is a promising method for controlling the chattering vibration of large-span bridges,and based on this,eight different IBDs including TMDI were proposed and optimized by comparative study of simply supported beams.In bridge seismic mitigation,TMDI has different vibration amplitudes not only longitudinally but also transversely.According to this theory,a threedegree-of-freedom model of a tuned mass damper can be established to optimize the parameters of TMDI in bridge application.In addition,standardized simplified procedures[110–112]for the design and evaluation of bridge comfort can be carried out based on the HiVoSS guideline[113].
In bridge applications,TMDI is a common method of vibration control,and its design optimization can further improve the structural performance and safety of bridges.The following are some comments[114–116]:
1.The structural characteristics of the bridge have an important influence on the optimal design of TMDI.For example,factors such as stiffness,natural frequency and mass distribution will determine the parameter configuration of the TMDI.Higher stiffness may require larger tuned mass dampers and the selection of appropriate vibration modes for control around the natural frequency.It is also necessary to consider the geometry and material properties of the bridge to ensure that the design of the TMDI matches the actual conditions of the bridge.
2.The structural properties of the bridge have an important influence on the optimal design of the TMDI.For example,factors such as stiffness,natural frequency and mass distribution will determine the parameter configuration of the TMDI.Higher stiffness may require larger tuned mass dampers and the selection of appropriate vibration modes for control around the natural frequency.It is also necessary to consider the geometry and material properties of the bridge to ensure that the design of the TMDI matches the actual conditions of the bridge.
3.Bridges are subject to various external environmental loadings in actual use,such as wind loads and traffic loads.These loadings will cause bridge vibration and may interfere with the control effect of TMDI.Therefore,in the optimized design of TMDI,it is necessary to comprehensively consider these external environmental loadings and determine the corresponding vibration control strategy.This can include adjusting the TMDI parameters according to different working conditions or adopting adaptive control strategies to ensure that the TMDI system can effectively control bridge vibration.
4.In order to realize the best control effect of TMDI,the bridge vibration can be monitored in real time using a real-time monitoring system.With the data obtained from real-time monitoring,the parameters of TMDI can be adjusted in real time to adapt to different vibration conditions and environmental changes.This real-time control strategy can improve the adaptivity and control accuracy of the TMDI system for better control of bridge vibration.
5.The optimal design of TMDI can involve several objective functions,such as minimizing structural vibration,minimizing coupling forces,and maximizing system reliability.The combined consideration of these objectives can be achieved by a multi-objective optimization algorithm.Such an algorithm can provide a series of optimal trade-offs for decision makers to select the most suitable design solution for practical applications.
In summary,the optimal design of TMDI in bridge applications requires comprehensive consideration of bridge characteristics,multimodal vibration control,external environmental loading,and other factors,combined with real-time monitoring and control,as well as integrated multi-objective optimization methods to achieve the best vibration control results.This will help to improve the structural performance and safety of bridges.
5 Conclusions
TMDI has drawn much attention due to its ability to achieve vibration control and energy harvesting under certain conditions.The introduction of TMDI can effectively passively suppress the vibration of the system,but it may also make the dynamic response of the system more complex under external loads.Therefore,finding the optimal optimization scheme that enables the system to maintain good vibration control while maximizing energy harvesting is important.This paper reviews the development of TMDI in terms of design,implementation,development status,optimization strategies,and applications in a wide range of engineering fields since 2002.The main focus is on the implementation of vibration control by TMDI,the impact of energy harvesting,and improvements to overcome the shortcomings of engineering vibration control.From this review,it can be seen that research on TMDI is constantly increasing in both quantity and depth.Future work prospects include the following aspects:
(1) Previous studies have shown that a reasonable approach to structural performance analysis is to evaluate the structural performance based on reliability,in order to the general safety or fitness of the structure.However,the existing performance evaluation of the structure-TMDI system is often based on the structural response indicators under deterministic inputs or the mean or variance of the structural response under white noise random excitation.This stochastic simulation method requires a huge amount of computational work to obtain reliable results that meet requirements,so it is crucial to find a reliability-based structural vibration control theory.
(2)Currently,most of the research on the optimal design of a TMDI focuses on optimizing the TMDI tuning method and connection arrangement to improve the motion control efficiency of certain given primary structures.To examine the vibration control effectiveness of TMDI,the fixed point theory may provide a means to optimize its design parameters.Based on the optimal design of TMDI in MDOF structures,the best parameters,including mass ratio,inertia ratio,frequency ratio,and damping ratio can be determined.
(3)Passive TMDI can reduce the cost of vibration control,especially by reducing the mass of the TMDI inertial device while maintaining satisfactory vibration reduction.
(4) The efficiency of TMDI in energy harvesting is often too low.Therefore,it is necessary to ensure efficient energy harvesting while maintaining the comfort of high-rise buildings or controlling the vibration amplitude within a reasonable range.For example,some semi-active or active control designs can be introduced into TMDI to realize real-time variation of TMDI parameters with the vibration environment to achieve optimal vibration reduction while achieving efficient energy harvesting.
(5)The development of motor,intelligent material,and metamaterial technologies has improved and upgraded classical inertial devices.This has led to the design of many controllable inertial devices that have been put into practical use.During this design process,the control methods of inertial devices have also been summarized and evaluated.
(6)There are some fundamental issues and challenges that need to be further researched at present.In the future,a more universal TMDI device and design approach could be developed and utilized across various fields.However,before this can be achieved,more advanced and simplified control theories need to be introduced so that TMDI can be widely applied in practice.
In conclusion,this paper reviewed the research progress of resonant mass-damper-inerter in design schemes,linear and nonlinear optimization,energy harvesting,and engineering practical applications,and looked forward to future research directions.We hope that this review can provide ideas and inspiration for the research and application of TMDI in new technologies.
Acknowledgement:This paper’s logical organisation and content quality have been enhanced,so the authors thank anonymous reviewers and journal editors for assistance.
Funding Statement:This research was funded by the Anhui Provincial Natural Science Foundation(Grant No.2008085QE245),the Natural Science Research Project of Higher Education Institutions in Anhui Province (Grant No.2022AH040045),the Project of Science and Technology Plan of Department of Housing and Urban-Rural Development of Anhui Province(Grant No.2021-YF22),the National College Student Innovation and Entrepreneurship Training Program Project(Grant No.202210878005).
Author Contributions:Conceptualization,X.K.;Data curation,Q.H.;Formal analysis,Q.H.;Investigation,X.K.,Q.H.and X.J.;Methodology,X.K.,Q.H.and Z.W.;Supervision,X.K.,S.L.and Q.H.;Validation,X.K.;Writing–original draft,X.K.and Q.H.;Writing–review–editing,Q.H.and J.T.All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials:No new data were created or analyzed in this study.Data sharing is not applicable to this article.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
杂志排行
Computer Modeling In Engineering&Sciences的其它文章
- A Study on the Transmission Dynamics of the Omicron Variant of COVID-19 Using Nonlinear Mathematical Models
- Novel Investigation of Stochastic Fractional Differential Equations Measles Model via the White Noise and Global Derivative Operator Depending on Mittag-Leffler Kernel
- Saddlepoint Approximation Method in Reliability Analysis:A Review
- Recent Advances on Deep Learning for Sign Language Recognition
- A Survey on Blockchain-Based Federated Learning:Categorization,Application and Analysis
- Full-Scale Isogeometric Topology Optimization of Cellular Structures Based on Kirchhoff–Love Shells
