基于脉冲间隔分布矩阵的抗抖性改进算法

刘国满，王守国，王俊岭，孔令磊，吕鹏

（1.北京理工大学 信息与电子学院, 北京 100081；2.空军装备部驻北京地区第一军事代表室, 北京 100854；3.中国科学院 空天信息创新研究院, 北京 100094）

雷达信号分选是电子侦察中关键的一环，它的主要任务是将截获的脉冲密度流进行分类，使得属于同一部雷达的信号脉冲被分在同一类中[1].传统雷达信号分选主要分为两个步骤：预分选和主分选.通常将利用脉冲重复间隔（PRI）的分选叫做主分选，而利用其他特征参数的分选叫做预分选[2-4].

主分选的目的是分选出信号的PRI 值，得到辐射源的脉间调制信息.直方图法是进行主分选最常用的方法，包括累积差值直方图法（CDIF）、序列差值直方图法（SDIF）和PRI 变换法[5-7].PRI 变换法的主要思想在于将PRI 转换为相位信息，利用相位抵消来抑制谐波，保留真实的PRI 值，该算法具有较好的谐波抑制效果，但对脉冲丢失和PRI 抖动很敏感，且当脉冲数量增多时，计算量急剧增大[8].2000 年，KENICHI 等[9]针对PRI 变换法抗抖性差、相位误差累积的问题，提出了一种基于可变起始点和交叠PRI 箱的改进算法.然而，由于PRI 变换法相位抵消，抑制了参差信号的帧周期，无法对参差信号进行测量[10-12].2021 年，王俊岭等[13]基于脉冲间隔分布矩阵（PIDM）对PRI 变换法进行了改进，避免了参差信号帧周期过度抑制的问题.但是该算法抗抖性差，无法对抖动信号进行测量.除此之外，利用深度学习的方式进行信号分选也成为了研究热点，然而其技术尚不成熟，难以用于工程实现[14].

PIDM 算法抗抖性差，而改进PRI 变换法具有良好的抗抖性.因此，本文借鉴改进PRI 变换法交叠PRI 箱的思想对PIDM 算法进行了改进，并对门限的计算方式做了修改，使其具有了一定的抗抖性（5%～10%）.最后，对交叠PRI 箱所引起的过门限值增多的现象进行了聚类分析，以簇均值（子序列提取）或最小值（主周期提取）作为真实PRI 值.

1 改进PRI 变换法及PIDM 算法

1.1 改进PRI 变换法原理和缺陷

PRI 变换公式为

其中，τ为时延，τ=tn-tm且τ＞0.

传统的PRI 变换法存在抗抖动性差、相位误差累积等问题，为此有交叠的PRI 箱和可变时间起点两种常用改进方式.

交叠PRI 箱是指：假设ε是PRI 的抖动上限，bk和τk分别为第k个PRI 箱的箱长和中心，b为固定箱长，则

虽然改进PRI 变换法相对于传统PRI 变换法具有了一定的抗抖性，但两种方法都存在由于相位抵消而引起的帧周期过度抑制问题，无法对参差信号进行有效的分选.

1.2 PIDM 算法的原理和缺陷

PIDM 是一个K×N的矩阵，其中第(k,n)个元素为

式 中：N为 脉 冲 数；n为 脉 冲 号；k为PRI 箱 号.则 第(k,n)个元素所代表的意义为与第n个脉冲的时间差的绝对值等于τk的脉冲的个数.

如图1（a）所示，对于重频固定信号，其PRI 的箱号为170，若忽略起始与终止的边界位置，其PIDM矩阵会在重频固定周期值及其子谐波对应的行幅度值为2（白线处），而在其他行幅度为0（黑色区域）.

对谐波而言，其存在于高阶直方图中.理想情况下，在低阶直方图中，当元素(k,n)值为2 时，通过对第n个脉冲添加抑制标记，使其不参与高阶直方图的运算，可以有效地抑制谐波.如图1（b）即为抑制子谐波情况下的PIDM 矩阵，只在主周期处幅度为2，其余区域幅度为0.

非理想情况下，干扰信号会使脉冲在小于真实PRI 处幅度值达到2（例如存在许多干扰脉冲与信号脉冲的时间差值为二分之一真实PRI 时，二分之一真实PRI 处幅度值将会达到2），从而使得真实PRI处被误判成了子谐波而被抑制.为此采用抑制子谐波的矩阵M和不抑制子谐波的矩阵Mt同时计算.由于信号脉冲仅与前后两个脉冲时间差值为真实PRI 值，所以在低阶直方图中，Mt矩阵元素幅度最大为2，若大于2 则必然存在干扰脉冲（例如当干扰脉冲与信号脉冲时间差值小于箱长），此时取消该脉冲抑制标记，使其能参与高阶直方图的运算.计算M矩阵中每一行幅度值大于等于2 的元素个数，进行过门限检测，过门限的行所对应的PRI 值即为真实PRI 值.

对于参差信号，按以上方式得到的为主周期，要提取子序列的PRI 值需要进一步处理.将上述过门限的行称为主周期行，将Mt矩阵中主周期行中幅度值大于等于2 的元素提取出来重新生成M矩阵.最后，计算新的M矩阵每一行中幅度大于等于1 的元素的个数，进行过门限检测，将过门限的行称为子序列行，子序列行所对应的PRI 值即为子序列的PRI值.图2 为参差信号的PIDM 矩阵图，子序列箱号为200、250、300，其中幅度为1 代表着子序列及子序列的谐波，幅度为2 代表着主周期.

图2 重频参差信号PIDM 矩阵图Fig.2 Matrix diagram of repeated frequency uneven signal PIDM

PIDM 算法克服了PRI 变换法参差信号帧周期过度抑制的问题，但抗抖动性差.

2 改进PIDM 算法

2.1 算法原理

传统的PIDM 算法解决了PRI 变换法无法分选参差信号的问题，但抗抖性差，而改进PRI 变换法具有良好的抗抖性.为此，本文借鉴PRI 变换法交叠PRI 箱的思想对PIDM 算法进行了改进.当图1（a）信号存在抖动时（5%），PRI 值会偏移到附近的PRI 箱中，导致PIDM 矩阵中幅度为2 的元素变成了两个幅度为1 的元素，所以在对某个元素进行幅度判断时，应将该元素同脉冲下，相邻PRI 箱的幅度之和作为幅度值.而对于求和的PRI 箱的范围，可以以改进PRI 变换法交叠PRI 箱的上下限为准.

2.2 算法流程

改进PIDM 算法分为3 步：生成PIDM 矩阵、主周期行提取、子序列行提取.

2.2.1 PIDM 矩阵生成

此步骤最终得到两个矩阵Mt（不进行子谐波抑制的PIDM 矩阵）和M（进行子谐波抑制的PIDM 矩阵）.具体流程如下：

（1） 初始化每个箱的中心和上下限；

（2） 计算Δt=tn-tm；

（3） 若Δt小于最小PRI 值或大于最大PRI 值，则跳到（2）；

（4） 计算Δt所处的PRI 箱箱号k=ceil((Δt-Pmin)/b)；

（5） 计算Mt；

（6） 计算PRI 箱交叠范围[kmin，kmax]，若kmin小于1 则等于1，若kmax大于PRI 箱数则等于PRI 箱数；

（7） 分别计算Mt矩阵脉冲n和m交叠范围内元素幅度和，若大于2，抑制标记清0；

（8） 若脉冲m和脉冲n抑制标记皆为0，则

（9） 分别计算M矩阵脉冲n和m交叠范围内元素的和，若和等于2，抑制标记置1；

（10） 跳到（2），直至直方图计算完成.

2.2.2 主周期行提取

主周期行为M矩阵中幅度为2 的元素的数量超过门限的PRI 箱，主周期行对应的PRI 值为主周期值.具体流程如下：

（1） 初始i=1，若i大于PRI 箱数，则跳到（5）；

（2） 计算第i个PRI 箱的交叠范围[kmin，kmax]，若kmin小于1 则等于1，若kmax大于PRI 箱数则等于PRI箱数；

（3） 初始j=1, 若j大于脉冲数，则i加1，跳到（1）；

（4） 计算M矩阵第j个脉冲在交叠范围内元素幅度之和s，若和大于等于2，则主周期行数组main-Num 第i个元素加s，j加1，跳到（3）；

（5） 计算门限，并进行过门限检测；

（6） 将过门限的值进行排序、聚类，并选择每一类的最小值为该类PRI 值，此步骤得到的结果为信号的主周期值.

2.2.3 子序列行提取

将Mt矩阵主周期行中幅度值大于等于2 的元素所对应的脉冲提取并重新生成M矩阵（每个主周期行分别提取），子序列行为中新的M矩阵幅度等于1的元素数量超过门限的PRI 箱，子序列行对应的PRI 值为参差信号的子序列值.具体流程如下：

（1） 将Mt矩阵中主周期行交叠范围内幅度和大于等于2 的元素所对应的脉冲提取；

（2） 利用（1）提取出的脉冲计算M矩阵；

（3） 计算新的M矩阵中每个PRI 箱交叠范围内幅度和大于等于1 的元素个数；

（4） 计算子序列门限，将（3）的结果进行过门限检测；

（5） 将（4）的结果进行聚类并计算每一类的平均值，将平均值作为该类PRI 值；

（6） 将（5）得到的子序列值与主周期值进行计算，得到信号的调制类型和PRI 值.

2.3 门限选择

PIDM 算法门限遵循3 个原则：观察时间原则、抑制谐波原则、消除噪声原则.

NELSON 等[7]中主周期行门限选取公式如下：

式中：第一项为噪声门限；第二项为时间门限，第三项为谐波门限；α、β、γ 为可调系数，ST为时间长度，τk和bk分别为第k个PRI 箱的中心和箱长，p为脉冲密度，Ck代表Mt矩阵中第k个PRI 箱中幅度值大于等于2 的元素个数.本文对噪声门限和公式进行了更正且bk采用交叠箱长，谐波门限Ck以脉冲在交叠范围内元素幅度之和来进行比较且加一个常数.新的门限如下：

根据仿真测试，α、β、 γ、c分别为3，0.1，0.85，10.子序列行门限如下：

式 中： α′、 γ′为 可 调 系 数；Ck′代 表Mt矩 阵 中 第k个PRI 箱中幅度值大于等于1 的元素的个数；E(X)为噪声均值；D(X)为噪声方差.E(X)与D(X)公式如下：

经仿真测试，α'为3，γ'为0.9.

2.4 聚类分析

由于交叠PRI 箱和元素幅度计算方式的影响，过门限的PRI 值实际上是连续的一段，为此需要对过门限的值进行聚类，并以每一类的均值或者最小值作为该类的PRI 值.通过数据分析，过门限的PRI值存在由小到大排列的顺序，且同一类的PRI 值连续，为此可将误差在5 个PRI 箱以内的数据归为一类.以求算均值为例，具体流程如下：

（1） 将第一个过门限的PRI 值作为第一类的均值并令i=2;

（2） 若i大于过门限的PRI 数则退出；

（3） 若第i个PRI 值的箱号与第i-1 个PRI 值的箱号差值在5 以内，更新该聚类均值，第i类PRI 数加1，否则将第i个PRI 值作为新聚类的均值；

（4）i加1，跳到（2）.

3 仿真测试

本文对改进PRI 变换法、PIDM 算法和改进PIDM算法进行了对比，以验证改进PIDM 算法的优点.以下仿真参数均为PRI，单位为μs.

3.1 带抖动的重频固定信号

图3 为经过1 000 次蒙特卡洛仿真得到的结果，横轴为3 个信号的真实值，纵轴为误差值.由于PIDM算法在信号存在抖动量时，无输出的PRI 值，即结果集为空，所以无法画出其曲线.通过对比可知，PIDM算法完全无法测量带抖动的信号；改进PIDM 算法在抖动量5%时效果仍较好，抖动量10%时偏差较大；改进PRI 变换法在抖动量10%时仍能精准测量.

图3 重频固定信号结果比对图Fig.3 Comparison diagram of repetitive fixed signal results

3.2 参差信号

通过图4 可知，改进PRI 变换法完全无法测量参差信号（无子序列PRI 输出），PIDM 算法与改进PIDM算法对参差信号的测量都具有良好的效果.

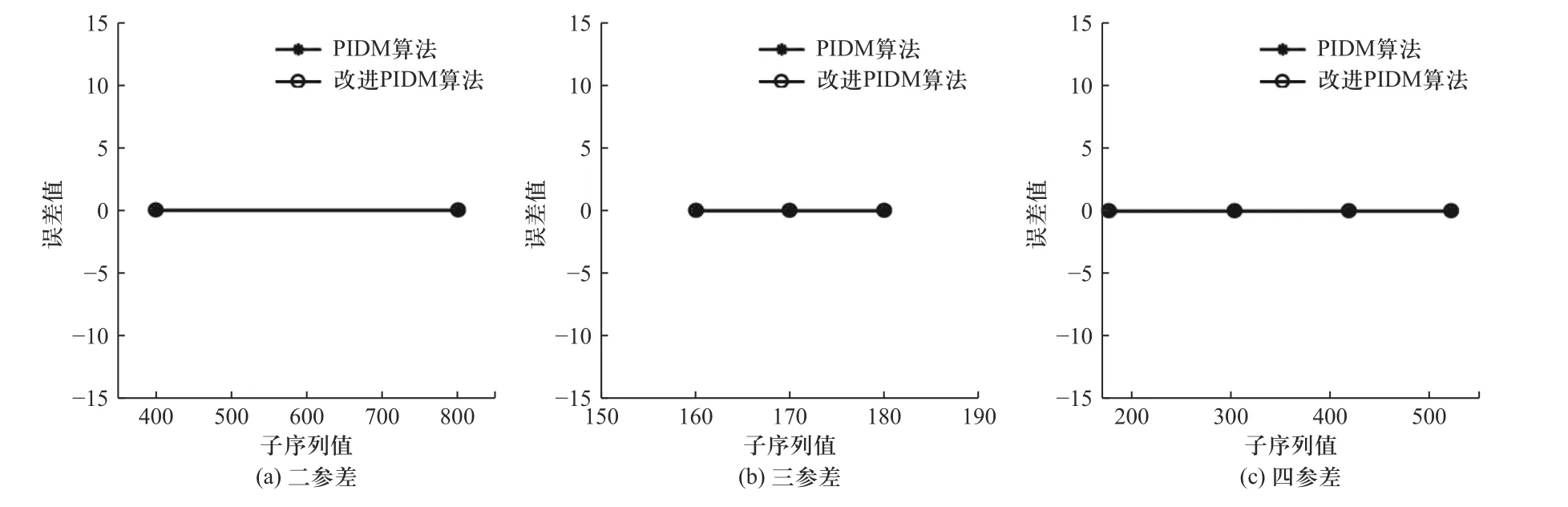
图4 重频参差信号结果比对图Fig.4 Comparison diagram of repetition staggered signal results

3.3 多种信号组合脉冲

表1 场景1 中3 参差信号子序列为200、220、370，3 个固定信号PRI 为300、460、610；场景2 中3 参差信号子序列为700、730、760，4 参差信号子序列为200、220、370、290；场景3 中3 参差信号子序列分别为200、220、370 和300、600、460，抖动量3%.由表1可知，改进PIDM 算法对多种信号的组合脉冲仍具有良好的分选效果.

表1 多种信号组合脉冲结果对比表Tab.1 Comparison table of pulse results of multiple signals combination

3.4 算法分选成功率

图5 是在不同场景下，本文算法参照文献[13]参数设置方式，使用随机信号参数，进行1 000 次蒙特卡洛仿真得到的不同信号的分选成功率.参数随机范围为10 μs～10 ms，参差子序列数3～4 个，以分选结果包含信号的PRI 及子序列值为分选成功.由于原始PIDM 算法在信号存在任何抖动时都无PRI输出，故其曲线无法绘出.

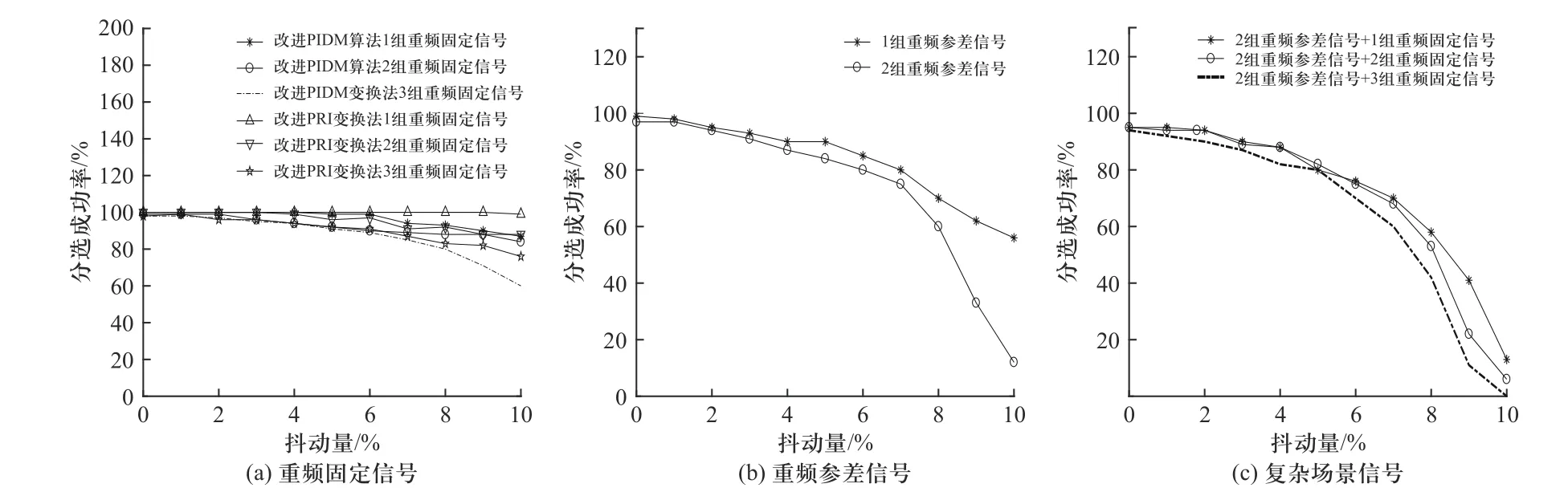
图5 改进PIDM 算法分选成功率图Fig.5 Sorting success rate of improved PIDM algorithm

由图5 可知，相较于PIDM 算法完全无法分选抖动信号，改进PIDM 算法在抖动量5%时，即便对2组重频参差加3 组重频固定的组合脉冲仍具有80%以上的分选成功率；在抖动量10%时，对有两组重频固定信号的脉冲分选率仍在90%以上；并且对抖动信号的分选成功率与文献[9]中改进PRI 变换法接近.

4 结 论

本文针对PIDM 算法抗抖性差的问题提出了改进算法：引入交叠PRI 箱的思想，修改了PIDM 矩阵幅度的计算方式，并对门限的公式做了改进、对过门限的结果进行了聚类分析.通过与改进PRI 变换法和PIDM 算法的仿真对比，验证本文算法在保留了对参差信号分选能力的基础上，具有了一定的抗抖性（5%～10%）.最后，本文参照文献参数设置的方式，通过蒙特卡洛仿真得到本文算法在抖动量10%时对两组重频固定信号分选成功率在90%以上；在抖动量5%时，对2 组参差信号和3 组重频固定信号的复杂场景分选成功率在80%以上.