基于果蝇优化算法的加速度计温控系统研究
2024-03-23刘宸歌黄丽斌
刘宸歌,黄丽斌
(东南大学仪器科学与工程学院,江苏 南京 210096)
0 引 言
硅微谐振式加速度计是一种潜在高精度的微机电系统(MEMS)加速度计,能将被测加速度信号转换为谐振器谐振频率变化并直接输出数字信号,降低信号检测与处理的难度,具有灵敏度高、分辨率高、动态范围宽、抗干扰能力强等优势,可广泛应用于导航制导、飞行器控制、重力测量等重要领域[1~3]。
对于现有的谐振式加速度计而言,温度变化会影响支撑梁弹性刚度、表头残余应力和噪声等,进而影响谐振器谐振频率[4~6]。目前PID 加速度计温控系统实验中,温控装置各模块放置不合理,温度信息不准确,进而影响温控系统的控制精度,最终导致加速度计输出不稳定[7]。本文首先搭建加速度计温控系统,通过对加热片进行热分析和加速度计的温度场仿真,验证加热片放置的有效性以及温控系统控制加速度计温度的可行性。在此基础上,设计了一种基于果蝇优化算法(fruit fly optimization algorithm,FOA)和积分分离的改进模糊PID控制算法,解决加速度计受温度变化影响导致的输出不稳定问题,控制内部环境达到设定目标温度并保持稳定,以此提升加速度计的温度性能。最后,通过实验对加速度计温控系统进行验证。
1 系统整体设计方案
本文系统由加速度计与温度控制回路组成,整体方案如图1 所示,系统采用以STM32F1CPU 为核心的温度控制回路。图中STM32 作为主控制器,通过输出脉冲宽度调制(pulse width modulation,PWM)波驱动程控电源输出不同的电压,调节加热片输出功率,控制封装件内部温度。温度传感器1检测加速度计封装壳体内部空气温度,实现精确测温;温度传感器2检测加热片温度,防止过热,保护器件。设计改进的模糊PID 算法,动态调整输入至程控电源的PWM波驱动占空比,从而实现封装件内部温度的精确控制。温度传感器采用TMP117,具有0.007 8 ℃分辨率。加热片采用聚酰亚胺(polyimide,PI)柔性薄膜式电加热片,具有电传导效率高、电阻稳定性强等优势。
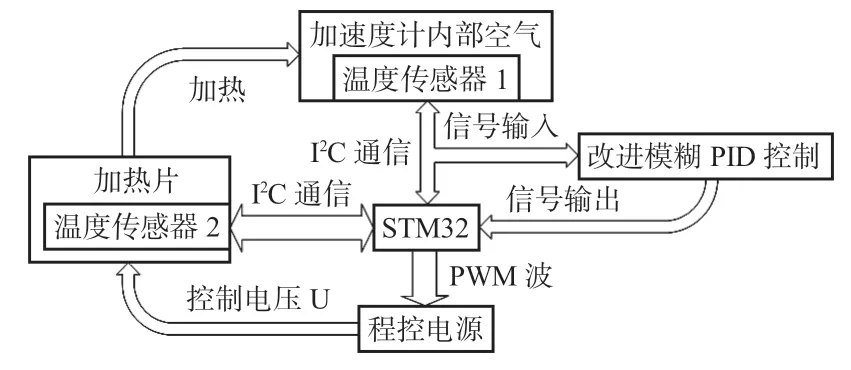
图1 温控系统整体方案设计
为使温度以最快的速度达到稳定状态,本文设计了分段式加热,针对不同的温度区间采取不同的加热方式,假设目标温度为T,内部空气温度(加速度计周围环境温度)为T1,加热片附近温度为T2。当T1与T的差值大于5 ℃时,以9 V恒压加热,使温度迅速接近预设温控点;当T1与T的差值小于5 ℃时,开始采用改进模糊PID控制加热,使温度稳定提升至目标温度附近;当T2大于60 ℃时,停止加热,器件保护。
2 加速度计整体封装模型与热分析
温控系统中加热片和温度传感器的放置位置对温度控制的精度有较大的影响[8]。温度传感器放置在封装壳体内,检测内部空气温度。加热片放置在封装壳体四周。对加速度计封装进行建模并对加热片进行热分析,通过Ansys仿真软件进行温度场仿真得到模型的温度分布,进而验证加热片放置位置的有效性。
加速度计整体封装如图2 所示。图2(a)为封装外壳模型,四周分别放置了4 个加热片。图2(b)为内部结构,表头通过引脚与印刷电路板(PCB)相连。PCB 温升不大,与表头无直接接触,可忽略其温度影响。

图2 加速度计整体封装模型
加热片热传递一维等效图如图3 所示,内部布满电阻丝,l,a分别为加热片的边长和厚度。
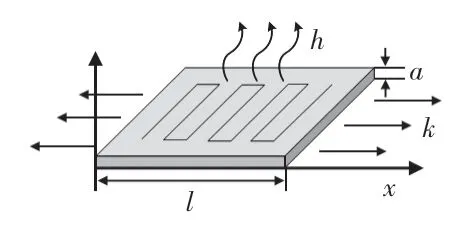
图3 加热片一维等效图
为了保证加热片在工作过程中的加热均匀性,分析其稳态下的热传递过程,根据经典热传导理论,加热片稳态下在x方向有式(1)成立[9]
式中T为加热片温度分布,h为热对流系数,k为热传导系数,x方向上的边界条件如式(2)所示
式中Rt,c为加热片四周的等效传导热阻,在不考虑热对流的影响下,有h=0,热功率密度q(x)=PE/al2。代入式(2)可解得一维分布如式(3)所示
式中f=0.5为热阻平衡系数,PE为电压加热产生的热功率,R0为加热片热阻。由式(3)可得温度分布差最大为R0PE/8,其中R0PE≪8。因此在对加速度计温度场仿真中加可看作均匀的恒温热源。
由于模型为对称结构,因此进行在热分析过程中可将三维的加速度计封装模型简化成二维模型,并利用Ansys软件对其进行有限元分析,简化后如图4(a)所示。

图4 加速度计二维模型与温度分布
利用Ansys仿真软件,可求解分析二维模型的温度场。仿真模型中对流换热系数为100 W/(m2·K)。整个外壳材料为可伐合金,处于25 ℃的外部环境中。加热片温度恒定为40.4 ℃,加热片分布在表壳四周,外壳上部与下部均无加热片放置,主要传热方式为热对流和热传导[10]。温度场仿真结果如图4(b)所示,外壳上部与下部温度为39.4 ℃,外部环境温度25 ℃,加热片温度为40.4 ℃,内部空气温度为39.9 ℃,与表头温差最大为0.1 ℃,在加速度计温控系统理想控制范围内,说明了放置加热片的有效性以及加速度计整体封装结构的可行性。
3 改进的模糊PID算法
3.1 模糊PID控制原理
PID控制为线性控制,将输入与输出进行比较,确定PID控制器的参数,对其差值进行一系列的PID 运算处理以达到理想的控制效果[11,12]。本文将采用增量式PID 控制,如式(4)所示
式中 Δu(k),e(k)分别为第k次运算的输出增量和误差值;KP,KI,KD分别为比例系数、积分系数和微分系数。
模糊PID 控制将模糊控制与增量PID 控制结合,利用模糊控制智能调节PID 算法的各部分增量。相比于传统PID控制,模糊PID具有鲁棒性强,响应速度快等优点[13]。由经验确定PID 参数KP,KI,KD的初始值,通过检测误差e(k)和ec(k)的值,并根据基于以往模糊经验理论和模糊控制原理来对PID 参数进行实时修正[14],其中,e(k)=r(k)-c(k),ec(k)=e(k)-e(k-1)。r(k)和c(k)分别为模糊PID控制的输入和输出。
3.2 改进的模糊PID控制整体流程
改进的模糊PID 控制是利用FOA 和积分分离优化对模糊PID 进行改进,如图5 所示。模糊PID 控制是将温度传感器检测到的温度值作为输入与输出进行比较,将得到的误差e和ec代入模糊控制器进行处理。利用FOA 优化模糊PID控制的初始参数。采用积分分离处理控制过程中误差过大的问题。
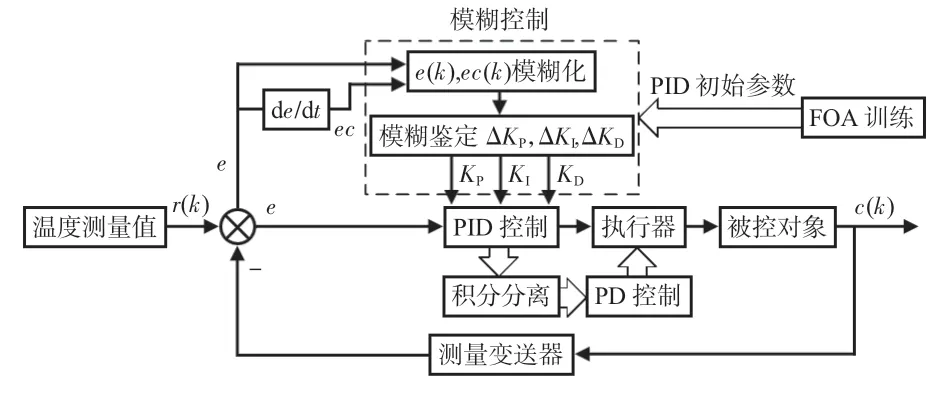
图5 改进模糊PID控制流程
3.3 改进模糊PID原理
3.3.1 积分分离优化模糊PID控制
由于温控系统外部环境较为复杂,控制过程中积分误差可能迅速变大,超出执行器允许的最大值,从而引起超调过大以及振荡[15]。本文设定在误差大于1 ℃时开始进行积分分离,将PID控制中的积分项去除,提高控制精度,控制方式如式(5)所示
式中γ为积分分离系数,取值如式(6)所示,ε=1 为误差允许阈值。式(6)如下
3.3.2 FOA优化模糊PID控制
为提高模糊PID 控制系统整体性能,其控制参数可以通过智能优化算法自动寻优。FOA 是一种群体智能算法,在复杂非线性优化问题求解方面有很大优势。能够快速搜索全局最优解,在保证系统控制精度的同时具有很强的实时性[16]。本文利用FOA 优化模糊PID 控制初始参数KP,KI,KD,提高了算法预测的速度和准确度。
优化步骤如下:
1)初始化FOA参数,确定最大迭代次数gmax,种群规模为s,令迭代次数g=0,果蝇根据实际控制要求,选择优化参数的范围。设置果蝇种群初始位置(Xaxis,Yaxis),选取其中的实数进行编码Xaxis=(x1,1,…,x1,p,…,xk,1,…,xk,p),Yaxis=(y1,1,…,y1,p,…,yk,1,…,yk,p),其中,Xk,Yk为第k个种群的横坐标,k=1,2,…,s;p为所需优化参数数目。为防止陷入局部最优,选取ρg为迭代步长,以自适应的方式不断调整寻优机制,如式(7)所示
2)给出果蝇Fi的随机方向和随机距离,rand()随机生成(0~1)之间的数
3)计算果蝇Fi与初始位置的距离Di和道浓度因子Si,如式(9)所示
4)将果蝇个体解码,代入适应度函数进行味道浓度判定,运行系统模型,得到性能指标,如式(10)所示
5)将步骤(4)得到的性能指标作为果蝇个体的适应值,判断是否满足停止条件,如满足,则结束优化得到最佳的PID参数,否则转至步骤(6)。
6)令g=g+1,由式(9)得到Si。比较Si和当前最佳浓度值Sbest,更新果蝇群的最佳味道和位置Xbest和Ybest。开始迭代循环,若g≤gmax,则回到步骤(2),否则,跳出循环,记录当前最佳位置和浓度。
为获取较为满意的优化过程,采用误差绝对值时间积分性能指标作为适应度评价函数Jbest。为防止控制输入过大,在加入控制输入的评分项。为避免超调,采用罚函数对超调量进行优先处理如式(11)所示
式中α,β,γ,ρ为各项加权值,且γ≫max(α,β,ρ);e(t)为系统输出误差;u(t)为PID控制器输入量;tp为到达稳态时间;σ(t)为超调量,eσ(t)=σ(t)-σ(t-1)。
计算FOA 训练模型的最佳适应度,令s=100,gmax=500,p=3,选择KP,KI,KD三个参数的范围,分别为[0 10],[0 1],[60,120]。得到迭代次数与适应度的关系,如图6所示,最佳指标函数值12.41,进而得到初始值KP=5.712,KI=0.387,KD=89。
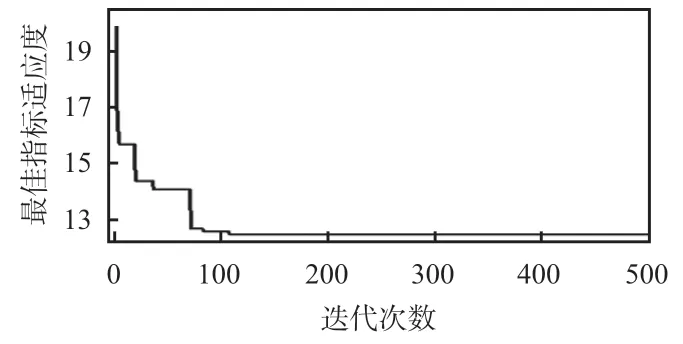
图6 FOA训练模型的迭代次数与适应度关系
4 实验结果
在标准大气压下,外界环境在常温(20~28 ℃)温度范围内波动,利用FOA改进后得到的初始值代入改进的模糊PID控制系统中,并利用控制系统将加速度计从常温20 ℃加热到40 ℃并保持恒定。在温度接近40 ℃时启动加速度计,记录改进前后温度随时间变化的数据,对比说明改进前后PID控制的稳态误差与控制精度的差异。
将初始值代入改进的模糊PID 控制中,得到改进模糊PID控制算法加速度计温度和时间的关系。图7(a)展示了PID、模糊PID和改进模糊PID算法中加速度计温度和时间的关系。选取了合适的参数后,相比于普通PID系统,模糊PID控制超调量减少了7 ℃,收敛时间缩短了80 s;改进的模糊PID控制超调量减少了9.8 ℃,收敛时间缩短了100 s。图7(b)展示了恒定40℃时模糊PID与改进模糊PID 控制对比关系。模糊PID 控制在恒定40 ℃时稳态误差为0.2 ℃,改进模糊PID 控制在恒定40 ℃时稳态误差减小到了0.1 ℃。与PID、模糊PID相比,改进模糊PID 算法的温度控制精度得到显著提高。
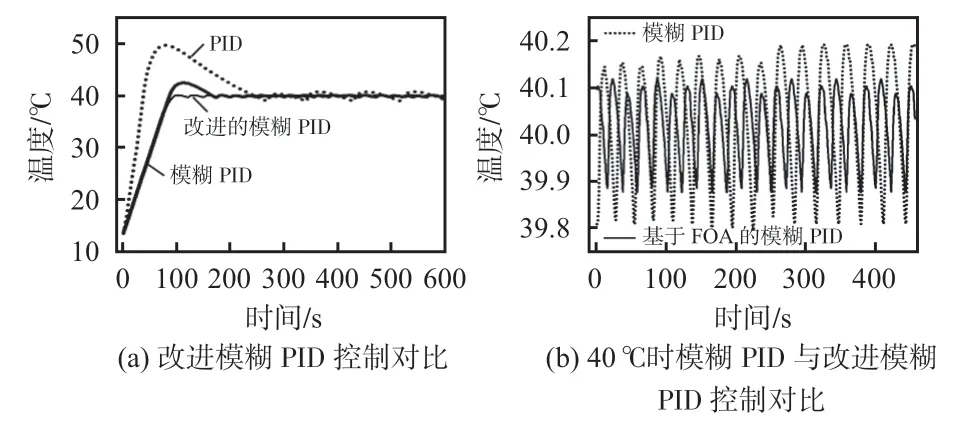
图7 改进模糊PID控制温度曲线
图8 展示了在常温(20~28 ℃)温度波动范围内与温控系统恒定40 ℃下加速度计的频差输出曲线。40 ℃下稳定时间为800 s,常温下稳定时间为2 500 s。通过频差输出曲线,计算出2种环境温度下加速度计启动20 min 后的零偏稳定性值。

图8 在常温和40 ℃环境下加速度计频差输出曲线
根据图8的数据,计算得到常温(20 ~28 ℃)温度波动环境下,启动20 min 后加速度计零偏稳定性为14.31 μgn,在40 ℃温控环境下零偏稳定性为4.09 μgn。
以上实验结果表明,通过合理的加热片布置,改进的模糊PID控制相比于普通的PID 控制有很大的改善,能够保证加速度计在温度波动很小的恒温环境下迅速启动,减小收敛时间,降低稳态误差,温度控制达到了很好的效果。
5 结 论
本文在对加热片进行热分析的基础上,结合Ansys 软件对加速度计整体封装模型进行温度场仿真,验证了温控系统加热片放置的有效性。利用FOA 和积分分离对模糊PID控制进行改进,加强了温度控制的准确性和稳定性。搭建加速度计温控系统的实验装置,验证了在常温下,与传统的PID控制相比,改进的模糊PID 控制算法能够更加准确地控温,温控系统收敛时间减少到60 s,超调量减少了9.8 ℃,稳态误差减少到0.1 ℃。与无温控相比,有温控的加速度计启动20 min 后的零偏稳定性值减少了71.4 %。实验结果验证了整体温控方案的有效性。
