柔性管异形表面结构对其涡激振动影响的数值研究
2024-03-22陈正寿杜炳鑫谢应孝
王 帅,陈正寿,杜炳鑫,谢应孝
(浙江海洋大学船舶与海运学院,浙江舟山 316022)
0 引 言
在海上石油深水作业系统中,隔水立管是浮式生产系统中由海底向船舶输送液体的基本装置。由于海洋立管长径比较大,同时须承受波浪、洋流等复杂海洋环境动载荷作用,通常沿管体会产生较显著的结构振动响应,由VIV 导致的疲劳破坏成为影响结构物使用寿命最重要的因素[1]。在VIV 发生过程中,当尾流区旋涡泄放频率接近结构固有振动频率时,会出现锁定共振现象,加速结构疲劳破坏。而立管一旦毁坏,将会产生严重的海洋污染和生态灾害,造成巨大的经济损失。因此,对VIV 抑制的研究具有重要的工程实际意义。
近年来,各国学者对柔性管的VIV 抑制开展了大量研究,主要抑制机理是通过对旋涡泄放进行控制,即控制边界层的分离。Choih[2]等把VIV 抑制方式划分为主动抑制和被动抑制两大类。Artana 等[3]试验了主动施加电磁力对VIV的抑制作用,Lee等[4]通过研究发现,主动施加旋转振荡圆柱体可以破坏尾涡生成,继而起到抑制VIV 的作用。由于主动抑制方式需要提供外部能源、结构复杂、成本高,在复杂的海洋环境中应用比较困难,而相比主动抑制方式,被动抑制方式则更加经济适用,一些被动抑制方式如螺旋列板[5]、整流罩[6]和控制杆等[7]被广泛应用。然而,被动抑制方式同样也具有一些不可避免的缺陷,如螺旋列板会显著增加阻力,整流罩的制造成本很高,其控制的有效性在很大程度上取决于流动方向,而且它们还容易受到海洋生物和极端环境的破坏。理论上讲,一个有效的VIV 抑制方式不仅可以消除涡流脱落,还应有助于降低流体力。因此,有必要进行进一步的研究尝试,以开发更加行之有效的VIV抑制装置。
Khalilpasha和Albermani[8]提出了通过纹理化管体表面抑制VIV的方法,由于纹理管(图1(c))在其纵向及横向上都具有局部小面,与具有等效性能的光滑管(图1(a))相比,纹理管可以显著增加屈曲传递能力,管体在承受轴向载荷时还能够提高能量吸收能力并改善破碎性能;Nikoo等[9]通过数值模拟工作研究发现纹理管消除了常规光滑管中出现的上部分支,并且锁振区间缩短,振动幅值显著减小,尤其是当管体在较大的速度工况下振动时,其振动抑制效果更加显著;刘小华等[10]对安装翼板扰流器的海底管线绕流进行了二维数值模拟,通过改变间隙比和翼板高度,探讨不同布置形式的翼板扰流器对海底管线绕流水动力特性的影响,研究结果表明,翼板高度为0.10D(D为管体外径)的Δ60°型翼型管(图1(b))的振动抑制效果最佳。

图1 不同类型管道示意图Fig.1 Example of different types of pipes
上述两类异形管无任何附加装置即可有效控制VIV,虽然它们可能具有广泛应用的潜力,但目前尚缺乏深入的系统研究。其中纹理化表面结构代表了一种新的壳结构设计理念,该结构已经被应用于水下自动机器人的设计制造,另外该结构的工业应用还包括各种管体设施(图2),用于轴向承压[11]和流动减阻。为进一步研讨表面纹理与扰流翼板结构对柔性管VIV 响应的影响,本文运用CFD 方法对细长纹理管、翼型管和具有等效性能的光滑管进行数值模拟综合研究,将数值计算结果做对比分析,以检验其VIV抑制的有效性。

图2 纹理化表面结构示例Fig.2 Example of textured surface structure
1 数值方法
采用双向流-固界面耦合计算方法,通过多物理场求解器STAR-CCM+[12]分别求解流体域和固体域的控制方程,双向FSI通过在流场域和结构域之间映射和交换数据来实现,计算流程如图3所示。首先在一个时间步长内,通过流场求解器计算得到管体上的流体力,并映射到管体结构单元上。然后通过固体位移模块计算管体运动变形,并作为流体网格运动条件反馈到映射界面。采用任意拉格朗日-欧拉(ALE)方案和径向基函数(RBF)插值方法,分别处理管体模型边界的移动和内部网格节点的移动。下一时间步则从求解更新后的计算域网格上开始计算,这个交互式过程将迭代重复进行。
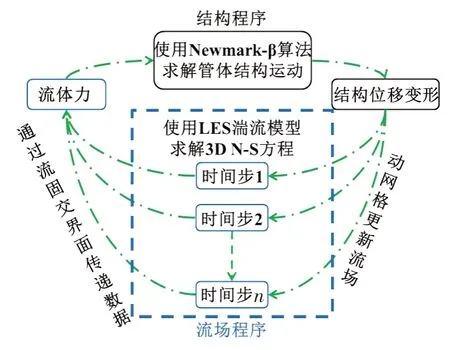
图3 双向流固耦合计算流程Fig.3 Procedure of two-way fluid-structure interaction
1.1 流场控制方程
数值计算模型是通过求解非稳态三维不可压缩的Navier-Stokes方程,结合大涡模拟(LES)与动态Smagorinsky SGS 模型来建立的。对于三维不可压缩粘性流体运动,由温度变化引起的能量转换可以忽略不计,仅需满足连续性方程和动量方程。
连续性方程的微分形式为
动量方程的微分形式为
式中,ui是流体速度分量,p代表压力,ρ为流体密度,μ为流体动力粘度系数,ν为流体运动粘度系数,xi和xj是流体单元的位置向量(i,j∈[]1,2,3),uˉ、pˉ分别表示速度和压力的时间平均值,τij为粘性应力张量。
1.2 结构动力学控制方程
将柔性立管简化为两端简支的Euler-Bernoulli梁模型[13],可以表示为
式中,EI表示结构弯曲刚度,T为立管顶张力,m为结构质量,c为结构阻尼,Fi为立管所受的水动力载荷分量。通过有限元法将式(3)离散化,采用Newmark-β方法进行求解。
式中,M、C和K分别是质量矩阵、阻尼矩阵和刚度矩阵,x(t)、ẋ(t)和ẍ(t)分别代表节点的位移矢量、速度和加速度,F(t)是流体域的流体载荷矢量。
2 数值模型
2.1 物理模型设定
为使该数值计算模型的设定具有可靠性并验证该数值计算方法的可行性,选取文献[14]中开展的细长立管试验模型作为本文数值模型的参考。同时,为使三类立管的数值计算结果具有可对比性,在建立数值计算模型时,将所需研究的三类管模型均在原试验光滑硬聚氯乙烯(UPVC)管的基础上外加一层橡胶层(具有极低结构弯曲刚度,杨氏模量设置为UPVC 管的万分之一左右),设置为内、外两层,三类管结构设计如图4所示。其中三类管的UPVC内管结构参数保持一致,这样三类管体结构的弯曲刚度相差不大;而对于橡胶层,由于三类管的结构差异性,在控制其基础尺寸一致的前提下,通过调整三类管橡胶层外管的密度参数值,使其总质量保持一致,模型具体参数设置详见表1。基于上述设定,三种类型管具有近似等同的尺寸参数、结构总质量与结构弯曲刚度。由此,能够在不影响内管性能的前提下,通过将橡胶层外管表面纹理化与横截面变形的方式,来探讨柔性管表面纹理与扰流翼板结构特性对其VIV响应的影响。
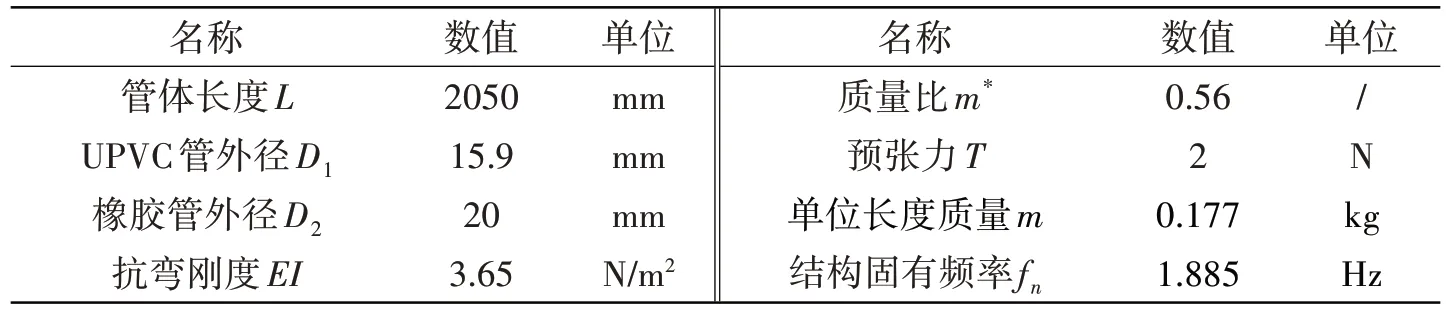
表1 数值模型的材料参数Tab.1 Material parameters of numerical model
2.2 计算域及边界条件
在计算域中模拟流体运动,如图5 所示,计算域的顺流向(IL)与横流向(CF)长度设置为45D×30D。管体中心在IL 方向(X轴)距离入口和出口边界分别为15D和30D,在CF 方向(Y轴)距离前后边界均为15D。计算域的边界条件设置如下:流体域的左侧入口边界设置为均匀速度入口,右侧出口边界设置为压力出口,参考压力设置为零,对称平面分配给前后边界,滑移壁面条件分配给顶部和底部边界,在管壁施加普通壁面边界条件,切向速度指定方式固定,剪应力指定为无滑移,即在该表面上流体速度与管体运动速度相同。
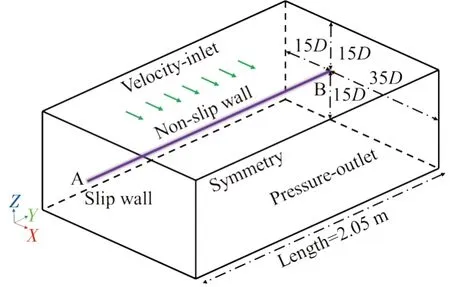
图5 VIV计算模型示意图Fig.5 Schematic of VIV calculation model
2.3 计算域网格拓扑划分
数值计算模型的三维视图如图6(a)所示。在计算域中对流体域网格拓扑结构采用多面体网格技术,该网格结构技术具有与六面体网格相同的计算精度,而与四面体网格相比则具有更好的网格收敛性与较小的网格依赖性。另外,在网格创建过程中采取了局部加密的策略,在靠近管体周围的计算区域生成精细的网格,而在远离该区域时则使用较为粗糙的网格。图6(b)所示为计算域X-Z平面上固体域与流体域近壁面边界层的网格拓扑图,而图6((c)、(d)、(e))则分别为三类管的结构有限元模型。其中,光滑管和翼型管整体是在沿管跨方向上按固定层间距拉伸的六面体定向网格,而纹理管由于橡胶层外管的结构特殊性,被划分为楔形四面体网格。另外,为了满足LES湍流模型对近壁面网格密度的计算要求,需要在与管壁相邻的流体区域生成非常精细的网格。通常保持y+≤1,以确保数值模型能够求解边界层并反映流动分离模式。y+的定义如下[15]:
式中,Δx为第一层的网格高度。
3 验证研究
3.1 时间步长与网格依赖性验证
数值计算中时间步长的选取与网格拓扑密度的确定,在数值结果的准确性方面起着重要的作用。为选取合适的相关计算参数,在本节中,选取刚性圆柱体做圆柱绕流计算,圆柱体直径D=0.02 m,长度L=πD,计算工况设定雷诺数Re=4000,考虑四种不同密度的网格尺寸和三种时间步长,对应6 种计算工况,相应编号列于表2 中。网格密度的控制参数包括圆周向节点数NC以及无因次参数ΔC/NC(ΔC为圆柱的周向长度),无量纲时间步长Δt*=Δt⋅V/D(Δt为实际计算时间步长,V代表流速)。拖曳力均值系数CD_mean、拖曳力均方根值CD_RMS、涡激升力均方根值CL_RMS和旋涡泄放频率fv等数值计算结果均列于表2 中,作为评判时间步长与网格依赖性的标准参数。结果表明:Case-3、Case-5 与Case-6 的fv、CD_mean、CD_RMS与CL_RMS的相对误差均在3%以内,由于节约计算资源的需要,本文只选取Case-3(NC=120,Δt*=0.01)的计算参数标准用于该研究的数值模拟工作。
3.2 流固耦合数值计算模型验证
为验证该数值计算方法的有效性,本文首先采用LES湍流模型对Re=200的固定圆柱绕流进行数值模拟,数值模型设定为:圆柱外径D=0.02 m,长径比L/D=8,表3 给出了数值计算结果与其它文献计算及试验结果的对比。可以看到数据对比较为一致,说明本文所采用的数值方法具有一定的准确性。
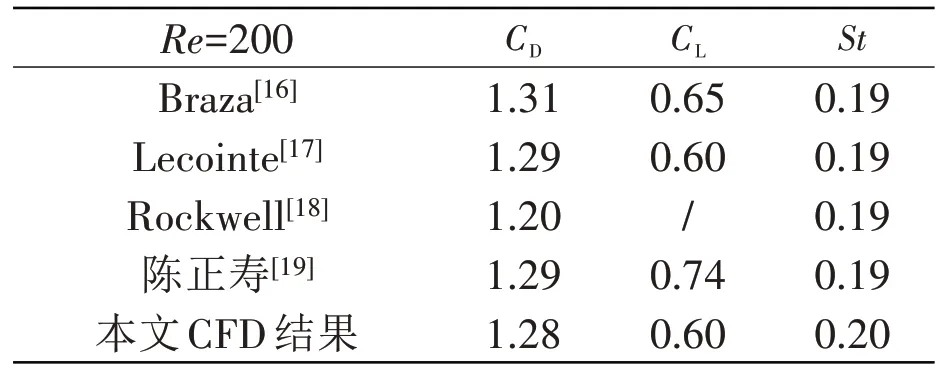
表3 圆柱绕流数据对比Tab.3 Data comparison of flow around cylinder
为进一步验证该数值模拟计算方法的准确性,本文参照文献[14]涡激振动试验研究中的细长柔性UPVC管模型,根据其相关试验参数重新建立数值计算模型,进行柔性振动管的数值计算,并将数值预报结果与文献[14]的相关试验结果进行对照分析,对比结果如图7 所示。可以看到,在不同速度工况下,数值模拟计算所得到的管体fv和均方根振动幅值RMSA/D,与原试验数据相比均具有较好的一致性,再次说明本文所采用的数值方法具有良好的可靠性,能够得到较准确的数值预报结果,可用于前期的数值模拟研究工作。

图7 柔性振动管试验和数值预报结果对比Fig.7 Comparison of flexible vibrating pipe test results with numerical prediction results
4 数值结果分析
4.1 振动响应特性分析
管体表面结构的改变,会显著影响其VIV 的响应特性。为了对比分析管体表面纹理化与扰流翼板的结构特性变化对其VIV 的影响,本文将翼型管、纹理管与光滑管的VIV 响应进行综合研究。三类管的均方根振幅RMSA/D如图8所示,图中y/L表示无因次化的管跨位置,约化速度Vr=V/fnD。
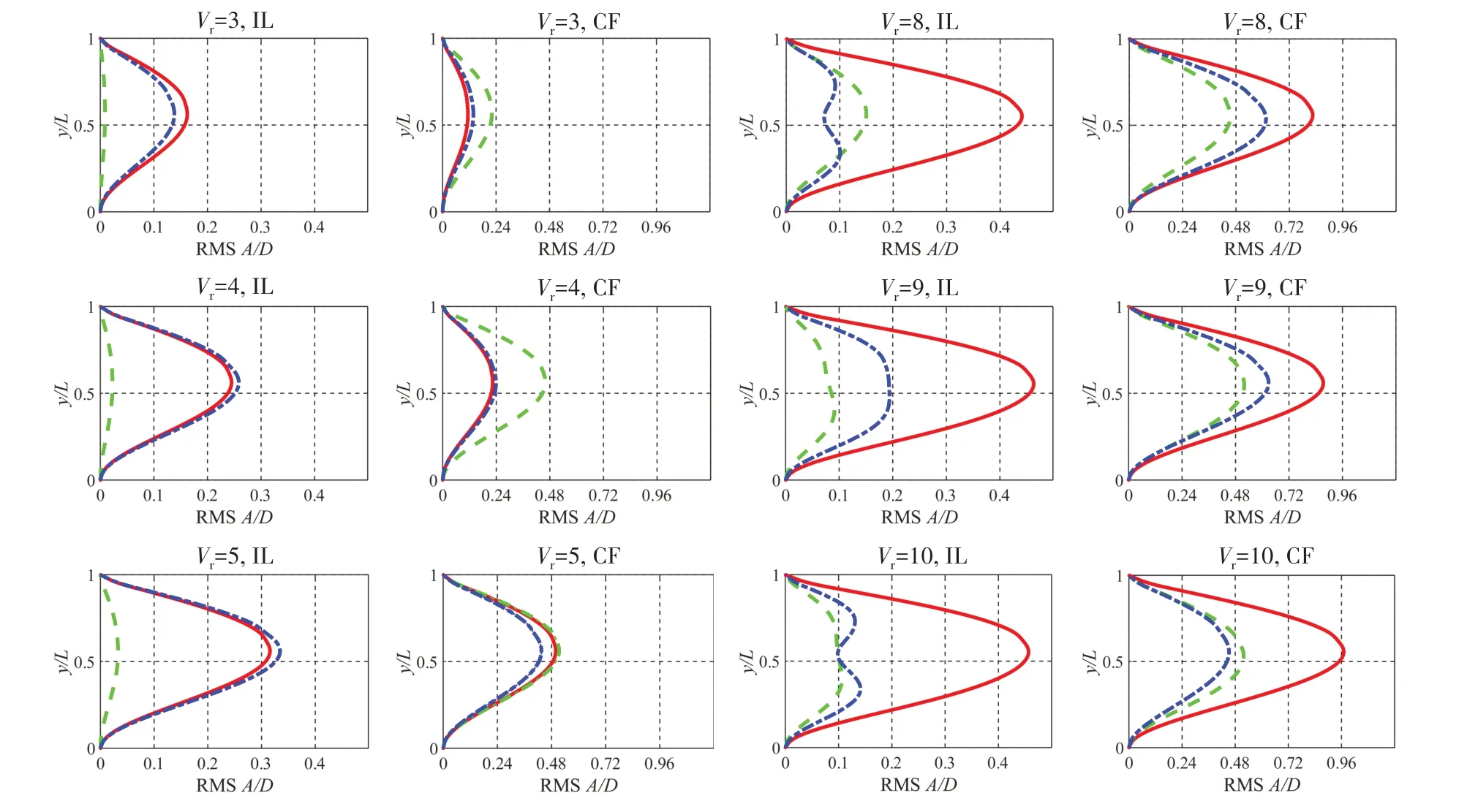
图8 三类管沿管跨的RMS A/DFig.8 RMS A/D of three types of pipes along the pipe span
首先在IL(顺流)方向上,可以看出,翼型管具有较显著的振动抑制效果,尤其是在三类管沿管体为同阶次振型的工况下,其RMS A/D值均远低于其它两类管。而在Vr=7、8两种速度工况下,沿各类型管体的主振型并不一致,通过对比发现,翼型管的振动抑制效果仍然较好,RMSA/D值在两种速度下较光滑管分别减少60%和66%。另外,纹理管在整个Vr范围内也具有较好的振动抑制效果,尤其是在Vr较大的工况下,振动抑制效果更加显著。其中在Vr≥7 的工况,纹理管出现了1、2 阶振动模态共存的情况,其RMSA/D值相较光滑管可达到减少80%的程度。在CF(横流)方向上,当Vr≤4时,翼型管和纹理管几乎没有发挥明显的VIV 抑制作用;但在Vr≥6 的工况下,两种异形管相比于光滑管,均具有更小的RMSA/D值,VIV抑制效果显著,其中翼型管的振动抑制效果又略微优于纹理管。
另外可以看到,在Vr<5 的工况下,因光滑管与纹理管还没有发生明显的涡激共振,两类管在IL 方向的RMSA/D值均大于其CF 方向的对应值;而在Vr≥5的工况,两类管在CF 方向的RMSA/D值则大于其IL 方向的对应值,柔性管体的涡激共振现象愈发明显。这是由于在柔性管的振动过程中,其IL 方向的振动响应频率一般是CF 方向的两倍,随着Vr增加,管体在IL 方向的振动响应频率能够更早地接近结构固有频率,首先进入锁振状态,从而产生相对较大的振动响应。随着Vr的进一步提升,柔性管在IL方向的振动响应则容易脱离锁振区间,而其CF方向的振动响应开始进入锁振区间,继而在CF方向产生较大的振动响应。区别于其它两类管,翼型管较早地在很低的Vr范围内就已经进入高频振动状态(由下文频谱分析可知),且在整个Vr范围内,其CF 方向的RMSA/D值一直远大于其IL 方向的对应值。
进一步由RMSA/D图可见,在Vr≤6 的工况下,三类管在IL 和CF 方向上的振动响应均表现为一阶振动模态占绝对主导。随着Vr增加,纹理管在IL 方向上开始出现一阶和二阶振动模态共同参与下的双模态振动响应。通过对比不同Vr工况下管体的振动位移在时间-空间上的分布,可分析流速对管体展向波形的影响。图9所示为纹理管在Vr=5、7、12三种速度工况下管体IL方向的位移-时程空间分布云图,其中横坐标为无因次化时间,纵坐标为沿管体轴向各监测点的无因次化位置,深色区域表示该瞬时振动位置偏离初始位置较大。由图可见,在Vr=5 时,管体振动过程比较稳定,展向波形呈非常规则的一阶驻波振动模态,相对应的结构振动响应频率f=3.35 Hz;当Vr=7时,可以看到纹理管的时-空分布云图展向波形存在一阶、二阶两种振动模态共存的现象,其中一阶驻波仅短暂存在,而二阶驻波则占主导地位;在Vr=12 时,纹理管时-空分布云图展向波形呈现出非常规则的二阶振动模态,因为长径比限制,立管IL方向的VIV由驻波主导。

图9 纹理管在IL方向的无因次振动位移时-空分布云图Fig.9 Spatio-temporal cloud of non-dimensional vibration displacement of textured pipe in IL direction
从上文对三类管RMS A/D图的分析发现,因一阶和一、二阶模态混合型振动在各速度工况下出现的概率较高,柔性管中间部位较容易出现大幅振动响应。在此选取柔性管中上部、y=1.1 m 位置处的振动轨迹来表征管体的运动状态。三类管在不同Vr工况下的振动轨迹如图10所示。
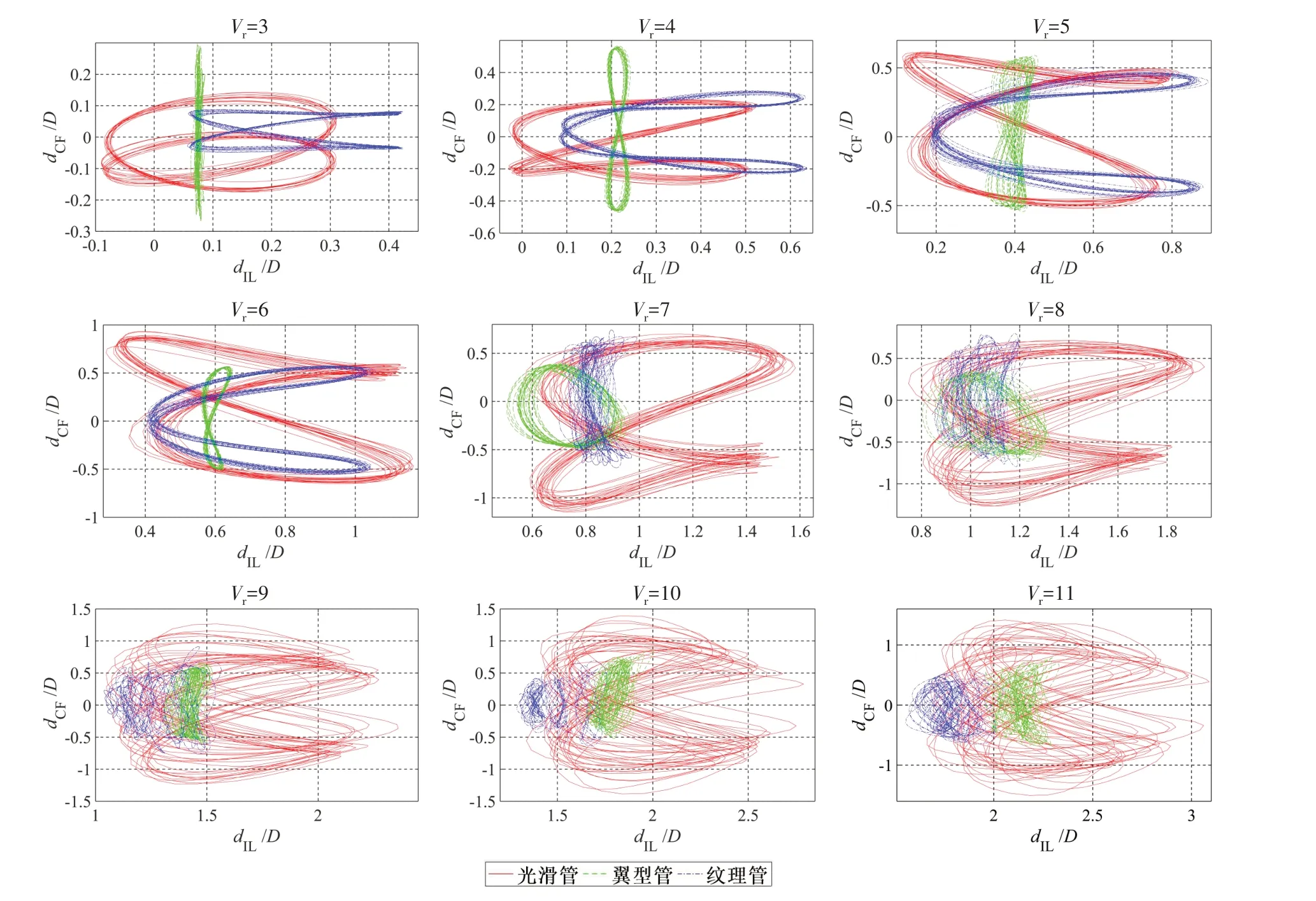
图10 三类管振动轨迹图Fig.10 Vibration trajectories of three types of pipes
可以看出,当Vr=3 时,翼型管在IL 方向的无因次化位移dIL/D相对较小,而其CF 方向的无因次化位移dCF/D明显大于其它两类管,且振动轨迹呈“1”字线条形;光滑管和纹理管在该Vr工况下的运动轨迹则表现为扭曲的“8”字形。在Vr=4、5、6 的工况下,翼型管的振动轨迹转变为明显的“8”字形。这表明管体在升、阻力的共同作用下,其IL和CF方向的振动耦合关系具有很强的非线性耦合特征,且VIV过程表现出典型的“双重共振”现象,即管体在IL和CF方向同时发生VIV。另外,在该Vr范围内,纹理管的振动轨迹则呈现出“C”字形与“8”字形相结合的形式,即在CF 的最大位移处,IL 方向上出现流向拉伸的趋势,并在CF方向上具有很强的对称性,振动平衡点基本不变;而光滑管的振动轨迹多为上下扭曲的“8”字形,且不具有对称性。当Vr=7、8 时,光滑管的VIV 过程在两个方向上均保持了很强的非线性耦合特征,其“8”字形振动轨迹仍然非常明显。而两种异形管的VIV 抑制作用在该Vr范围内显著增强。其中纹理管在CF 方向的最大位移处的流向拉伸趋势消失,其dIL/D值大幅减小,翼型管的振动轨迹由“8”字形变成“O”形,并且两种异形管的振动轨迹范围较光滑管均明显缩小。
在更高的Vr工况下,由于两种异形管一、二阶振动模态混合的现象发生较早,其振动轨迹均变得较为紊乱,且在IL和CF方向的振幅普遍较小,振动抑制效果更加显著。对于光滑管,因其一阶振动模态占主导,二阶振动模态隐约可见,其“8”字形振动轨迹仍清晰可辩,但每个周期的振动平衡点在不断发生变化。总之,随着Vr增加,三类管均呈现出高频率多模态共同振动特性,其在IL和CF方向的振动响应相互作用加剧,管体的涡激共振状态减弱,而相比于光滑管,两种异形管的振动幅值明显得到抑制。
图11 所示为三类管y=1.1 m 位置处的RMSA/D值随Vr提升的变化曲线。其中,如图11(a)所示在IL 方向上,翼型管在整个Vr范围内的RMSA/D值均远小于光滑管,与光滑管相比,其RMSA/D值缩减了60%~93%不等。而纹理管在Vr≤5时,其RMSA/D值与光滑管大小相当;当Vr=5时,其RMSA/D达到峰值,之后随着Vr增加而快速下降,在Vr=7时降至最小,之后呈波动逐渐上升趋势,但其RMSA/D值仍小于光滑管的对应值,振动抑制效果显著。另外,由图11(b)可见在CF方向上,在Vr<5的工况下,纹理管和光滑管的RMSA/D值基本一致,而翼型管的RMS A/D 值相对较大。随着Vr的增加,光滑管的RMSA/D值呈逐步增大的趋势,且明显大于两类异形管对应的RMSA/D值。在Vr>5的区域,两种异形管均表现出明显的VIV 抑制作用,其RMSA/D值随着Vr增加呈上下波动状态,其中翼型管的振动抑制效果要略优于纹理管。

图11 不同管的最大振幅响应Fig.11 Maximum amplitude responses of different pipes
综上所述,翼型管和纹理管均可以有效抑制管体的VIV 现象,尤其是在较大的Vr工况下,两种异形管的VIV 抑制效果更加突出,可同时显著减小管体在IL 和CF 方向上的振动响应,起到减弱管体疲劳破坏损伤的作用。
4.2 同步锁振现象
翼型管和纹理管的异形表面结构特征,会影响其尾流泄涡发放的稳定性,从而致使泄涡周期发生不同程度的变化。图12所示为三类管在不同Vr工况下CF方向的振动响应频谱图。可以看出,在Vr=2 的工况下,三类管在CF 方向的主振模态的对应频率fm基本一致。而在Vr=4 的工况,翼型管的fm值相较于其它两类管出现骤增,达到2.197 Hz,远大于光滑管和纹理管的对应值,同时也高于其fn值,这表明其振动响应较其它两类管首先进入锁振区间,并产生较大的RMSA/D值。

图12 三类管的振动响应频谱图Fig.12 Vibration response spectrum of three pipes
另外,在Vr≤6的工况下,光滑管和纹理管在CF方向的fm值均保持较好的一致性,但频谱峰值存在一定差异。在Vr≥7 的工况,纹理管和翼型管相对于光滑管则均具有较高的振动响应频率,它们的RMS A/D 值随Vr的提升也逐渐趋于稳定,同时亦远低于同一Vr工况下低频率振动的光滑管的对应值。对于纹理管,当Vr=8时,在其CF方向上出现多个振动能量较大的显著次振动频率,表现为明显的多频振动特征,振动能量开始变得较为分散,但显著次振动频率所具有的振动能量与主振动频率相比仍具有差异性。在Vr=9 的工况下,纹理管在CF 方向的多阶振动模态中,存在三个振动能量相当的主振动频率,并至少存在两个振动能量相对较小的次显著振动频率。而在更高的Vr工况下,这种多频共存的振动模态逐渐消失,振动能量再次变得集中。
在传统定义的锁定区域内,管体结构尾流区旋涡泄放频率不遵循固定圆柱绕流的斯特劳哈尔(St)规律,而是自我调节到结构的自然振动频率,即fv≈fn,从而引起系统发生涡激共振。图13(a)所示为三类管的无因次化泄涡频率f*=fvfn,可用来说明三类管的锁定共振状态,图中斜线为斯特劳哈尔频率(fSt,按St=0.20计算得到),而fv可以通过对升力时间历程曲线做快速傅里叶变换(FFT),将时域数据转换为频域数据后取主导频率得到。
由图可知,三类管的f*随Vr增加均呈上升趋势,且大致分为三个阶段。具体表现为先是在低Vr工况内,f*随Vr增加而平稳上升,之后进入锁振区间,上升幅度减缓,fv开始明显脱离fSt,并不同程度接近fn,而后振动响应脱离锁振区间,fv≈fSt。其中光滑管大致在Vr=6时,f*=0.98,在Vr=7时,fv与fn基本一致,其振动响应进入锁振区间,直至Vr=12时,fSt仍远大于fv,振动响应未脱离锁振状态,锁振区间较大。而纹理管的锁振开始点较早于光滑管,在Vr=6时,f*=0.96,fv明显脱离fSt并接近于fn,而当Vr=7时,f*骤升为1.5,fv回归fSt且与其保持一致,其振动响应脱离锁振状态,锁振区间较短。翼型管的锁振开始点则是在Vr=3时,明显早于光滑管和纹理管,并大致在Vr略小于5时,fv≈fSt,其振动响应脱离锁振区间。
应当注意的是,在锁振区间三类管的f*均稍大于1,这是一种“非经典”行为,是由于本文管体模型(空心管)的低质量比特性造成的。当管体处于来流中,管体开始往复振动,由于振动会产生附加质量,柔性管体的振动响应在锁振区间的f*随着来流速度的上升逐渐增大,尤其是低质量比柔性管模型,其增值更加明显,这种现象在很多试验分析中[20-22]均有出现,而在高质量比试验[23]的分析中,这种现象则并不显著。
三类管的St(由fv无因次化处理所得)变化曲线如图13(b)所示。可以看到,翼型管和纹理管的异形表面结构特征均增大了其St,高St表明流动中的振动占主导地位,而相对于纹理管,翼型管在整个Vr范围内则具有更大的St。总体来说,三类管的fv随着Vr增加均呈增大趋势。且与光滑管相比,纹理管和翼型管的fv得到了提升,其St也有所增大,同时表明异形管旋涡泄放周期减小。另外,翼型管特有的结构属性使其在整个Vr范围内一直以更高的频率振动,相应地也具有较小的RMSA/D值。相对于翼型管,纹理管具有小fv的同时,也能够有效降低管体的振动幅度。由于fv决定了单位时间内的应力循环次数,应力循环次数继而又影响到结构的疲劳性能。考虑到管体结构破坏受到振动幅值与振动频率两方面的作用,因此纹理管相较于翼型管具有更好的综合抑振效果。
4.3 流体力系数分析
如前文所述,一个有效的VIV抑制方式理应减小管体所受的流体力。图14所示为三类管的CD_mean值与CL_RMS值变化曲线,由图可见,三类管的流体力系数随着Vr增加而变化的趋势不尽相同。从图14(a)可以看到,相比于光滑管,两种异形管的CD_mean值均有显著减小。其中,在Vr<4的工况,翼型管具有相对较小的CD_mean值,且由上文可知在该Vr范围内,其IL 方向的RMSA/D值也远小于光滑管和纹理管的对应值。而在Vr>4 的工况下,纹理管的CD_mean值相对较小,同时随着Vr增加,其CD_mean值在Vr=6 时达到峰值,之后逐渐下降且趋于稳定在1.5左右,远小于其它两类管的对应值。
另外,由于周期性涡激升力的产生是造成管体结构发生VIV 的主要原因,因此可以通过减小管体所受的涡激升力,达到抑制其发生VIV 的目的。从图14(b)三类管的CL_RMS曲线图中可以看到,在大部分Vr工况下,两种异形管相比于光滑管均具有更小的CL_RMS值。同时可以观察到,三类管的CL_RMS值随着Vr增加均表现为先上升、后下降,最后趋于稳定的趋势。
总体来说,在大部分Vr工况下,两类异形管相比于光滑管均具有更小的流体力系数,其中纹理管具有相对较小的CD_mean值,而翼型管则具有相对较小的CL_RMS值。这是由于纹理管的局部小面与翼型管的截面凸起特性,能够导致流动分离点呈现局部随机性,并打乱沿轴向脱落的旋涡间的相关性,扰乱随时间变化的尾流压力场和剪切应力分布,继而减小管体的流体力系数,乃至降低其疲劳损伤和结构失稳的可能性。
4.4 尾流涡街模式
尾流区泄涡随柔性管的振动呈周期性发放,当VIV 响应增强时,一个周期内会有更多的旋涡泄放;相反,较弱的VIV 响应,则会有较少的旋涡泄放。图15 所示为三类管体管中截面展向的瞬时涡量云图,可见,异形管的异形表面结构对其旋涡泄放模式有显著的影响。图中分别捕捉到对应于不同Vr工况的“SS”、“2S”、“2P”、“2T”、“P+S”以及“T+S”型的旋涡泄放模式。

图15 三类管体管中截面展向的瞬时涡量云图Fig.15 Instantaneous vorticity contour plot at different cross-sections along three types of pipes
在Vr较低的工况下,三类管的泄涡模式一般为规则的“SS”或“2S”涡型。其中,翼型管更多的为平行“SS”涡型,且在同一Vr工况下,相比于其它两类管,其截面展向上有更多的旋涡泄放,这同时也说明翼型管的泄涡频率高于其它两类管。随着Vr增加,三类管在CF 方向的振幅不断增大,振动响应进入锁振区间,泄涡模式均相继切换为“2P”型。这其中,在“2P”型旋涡泄放模式中的双旋涡,在向尾流区下游发展的过程中,能量较弱的涡会逐渐消散,“2P”型泄涡模式又逐渐形成“P+S”型泄涡模式。随着Vr进一步增加,在光滑管的涡量云图中可捕捉到“2T”型旋涡泄放模式,即每个周期形成两组涡,每组涡包含三个旋涡,其中两个旋涡处于相同的方向,而另一个则相反。在高Vr工况下,翼型管和纹理管的泄涡模式中则再次捕捉到“2S”涡型,且其尾流涡街宽度在CF方向变窄,泄涡状态也较光滑管稳定,这是由于异形管的异形表面结构特性引起近壁面动量增加,导致流动分离的延迟所致。尾迹宽度被广泛用于表征钝体尾流的自然特征,可以定量描述尾流结构的拓扑结构,它们的改变会对管体压力分布产生显著的影响,导致流体动力特性发生变化,异形管在高Vr工况下尾迹宽度的减小,意味着其VIV抑制机制在该速度工况下发挥了明显作用。
再者,观察三类管中截面近壁面的瞬时涡量云图可以看出,在较低Vr工况下,光滑管和纹理管的近壁面剪切层围绕管体弯曲,直至管体由于周期性振动的原因而产生反向运动,旋涡才会沿管体向后脱落。而翼型管的旋涡较早地在管体翼板边缘以较小的角度脱落,形成更窄的尾流区域。随着Vr的增加,管体的振动响应加剧,尾涡脱落受管体大幅度振动影响,边界层分离点前移,纹理管和翼型管的分离涡沿管体的IL方向稳定脱落,这使得两类异形管的上下剪切层之间相互作用减弱,旋涡泄放所产生的涡激升力也同步降低,这也是两种异形管受力和振幅较小的成因之一。
5 结 论
本文运用CFD 方法,通过求解RANS 方程结合LES 湍流模型,建立了一个3D 数值计算模型,并用其研究了光滑管、翼型管和纹理管的振动幅值、响应频率、锁振区间、流体力系数与流场特性,计算结果表明:
(1)柔性管的表面纹理化和扰流翼板等表面结构特性均可以有效抑制管体的VIV响应,尤其是在约化速度相对较大时,能显著减小管体的振动响应幅值,起到减弱管体疲劳破坏对管体的损伤作用。
(2)翼型管和纹理管较光滑管的锁振区间均有大幅减小,但同时其旋涡脱离周期减小,斯特劳哈尔数相应增大,其中翼型管具有更高的频率比,而纹理管仅在较高的速度工况下,其频率比才明显高于光滑管。另外研究发现,管体在锁定振动过程中其无量纲频率比并不完全等于1,频率比的这种“非经典”现象,是因管体模型的低质量比所致。
(3)与光滑管相比,两种异形管均有效降低了其拖曳力均值系数和涡激升力均方根值的大小,也降低了结构疲劳失稳的可能性,并且其特有的异形表面结构特性还改变了管体的旋涡分离点,从而对其尾流涡街模式的形成产生一定的影响。
