艉轴大跨距轴系校中计算
2024-03-22谷志明杨蓬勃
谷志明,付 宇,李 珍,杨蓬勃
(广州船舶及海洋工程设计研究院,广州 510250)
0 引 言
近年来,业界主流论文较多围绕大型、超大型船舶轴系校中[1-4]展开研究,对中、小型船舶轴系校中研究较少,原因有三:一是中、小型船舶的轴系刚度较小,船体刚度较大,不易变形,同时艉部轴承长度较小,一般直线校中即可满足要求,中国船级社规范[5]允许螺旋桨轴直径小于250 mm的主推进轴系可不提交轴系校中计算书;二是在中、小型船舶的轴系校中计算中,艉部轴承被视为单点刚性支承[6-7],降低了轴系校中计算的复杂性和难度,计算结果也基本符合中小型船舶轴系的真实情况;三是中小型船舶一般附加值较低,而且种类繁多,研究价值随之降低。
轴系校中计算经常使用的方法主要有:三弯矩法、传递矩阵法和有限元法[6],这三种方法的理论基础均是经典力学方法,在本质上没有区别,但在具体实施过程中存在一定差异。魏海军等[8]利用传递矩阵法分析了艉轴多支承、油膜刚度。周瑞平等[9]通过对传统三弯矩方程在考虑外加力偶、轴段线性均布载荷以及轴段剪力变形影响等三方面的理论研究,提高了三弯矩校中的准确性。随着计算机的高速发展,有限元法计算速度和精度得到巨大的提升,另外随着商用有限元软件的升级迭代,有限元法的轴系校中变得越来越容易,而且也便于考虑船舶运行过程中的各种因素,如螺旋桨水动力、船体变形等[4,10]。
设艉管后轴承长度为Lb,L为支点距该轴承后端面的距离,大量文献均假定(或计算得出)艉管后轴承支承点在艉管后轴承的后半部分,比如在CB/Z 338-2005《船舶推进轴系校中》中,对白合金轴承,L=(1/7~1/3)Lb;铁梨木轴承,L=(1/4~1/3)Lb;橡胶轴承,L=(1/3~1/2)Lb。中国船级社的余华军[11]使用多点弹性支撑算出L=0.355Lb;大连海事大学的魏海军[8]研究了多点刚性支撑,结果表明采用刚性的模型去描述弹性的对象是不合理的,单点刚性支撑则选L=0.228Lb;张敏等[1]采用多点弹性支撑,将艉轴承沿长度方向分成N个分轴承,并假设每个分轴承刚度相等,为原轴承的1/N,算出L=0.43Lb;杨红军等[3]使用Hertz弹性接触模型描述轴承和轴的接触力学特性,但其首先假定L=0.25Lb。
本文选用有限元法,将轴系结构简化为Timoshenko 梁单元,建立有限元模型,考虑船舶轴系实际安装间隙,使用单向受压的非线性弹簧代替常规的弹簧单元,并基于赫兹接触理论计算轴段的载荷-刚度曲线,使用多点非线性弹性支撑模型对艉轴大跨距轴系进行校中计算。根据实船轴系布置情况,得到轴承支承点位于轴承前半部分的结果,并对艉管后轴承使用多种不同支撑模型进行校中计算对比。研究结果对工程设计和计算具有参考意义。
1 有限元模型建立
轴系结构通常可以简化为梁结构,本文选用Timoshenko梁单元,以广州船舶及海洋工程设计研究院设计的62 m 沿海客船轴系校中计算为例,参照CB/Z 338-2005,将轴系看作放置在刚性铰支上的连续梁,其长度自螺旋桨轴末端面开始,至齿轮箱大齿轮轴端面止,梁上作用着均布载荷、集中载荷(包括螺旋桨和齿轮箱大齿轮重量)等,边界条件为自由端,建立有限元计算模型,见图1。

图1 轴系校中计算模型Fig.1 Model of shaft alignment calculation
本船使用3 台K50-M 高速柴油机推进,采用三机三桨设计,单机额定功率为1342 kW,额定转速为1900 r/min,齿轮箱减速比为4.08:1,螺旋桨转速为466 r/min,其中左、右舷轴系全长为10.037 m,由艉轴、中间轴和齿轮箱的大齿轮轴组成,共有4 个轴承。其中,艉管后轴承参数如表1所示。艉管轴承采用油润滑,艉管后轴承支点位置取L=1/5Lb,艉管前轴承支点位置取轴承长度的中点。将有限元静态计算结果与CB/Z 338-2005 中改进的三弯矩法进行对比,轴系挠度曲线见图2,轴承负荷见表2,可见二者结果基本一致,证明本文有限元模型有效。

表1 艉管后轴承参数Tab.1 Stern tube rear bearing parameters

表2 轴承负荷(单位:kN)Tab.2 Bearing load
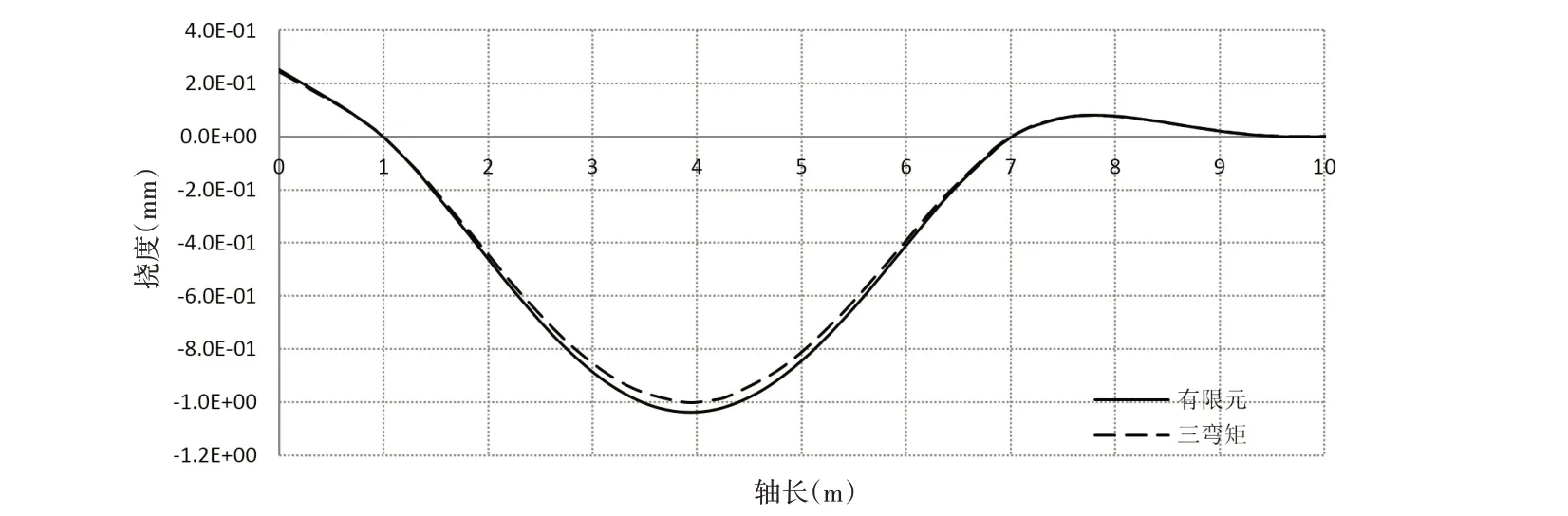
图2 轴系挠度曲线Fig.2 Shafting deflection curve
由表2 可知,齿轮箱后轴承支反力为负,说明齿轮箱后轴承脱空,这是规范所不允许的。而在艉管后轴承支点处,螺旋桨轴与艉管后轴承的相对倾角约为-3.35×10-4rad,虽然没有超过3.5×10-4rad,但其倾角为负值,观察图2 可发现在艉管后轴承支点处,艉轴为上翘状态,而不是下垂状态。显然,如果艉轴为上翘状态,此时艉管后轴承支承点位置应位于艉管后轴承的前半部分才是合理的(图3),即L>1/2Lb,远远超出CB/Z 338-2005的建议取值。
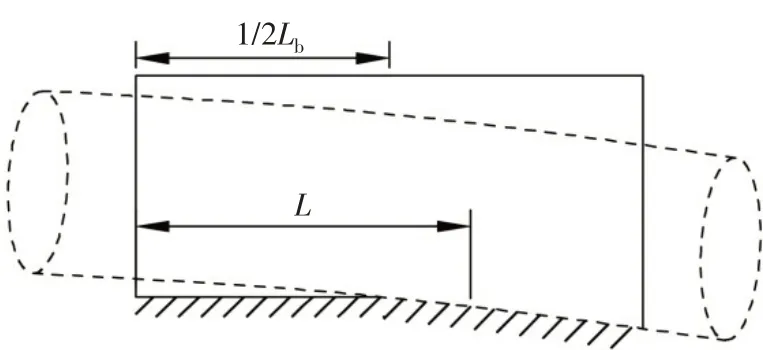
图3 艉轴上翘状态Fig.3 Propeller shaft upturned stat
2 艉轴后轴承等效支撑位置的计算
2.1 多点弹性支撑模型的建立
在船舶轴系校中计算中,考虑螺旋桨的悬臂作用,白合金艉管后轴承的支点位置一般取:L=(1/7~1/3)Lb,但是这种等效处理计算结果不能完整地反映轴承长度方向上各点的负荷分布情况,显然也不适用于图3 所示艉轴为上翘时的状态。为了提高轴系校中的准确性和有效性,将轴承沿长度方向分为n个轴承单元,如图3所示,其等效支点距离轴承后端面的距离为
式中:Fn为第n个分轴承处的负荷,Xn为第n个分轴承支点距轴承后端面的距离。
2.2 轴承安装间隙的处理
在轴系安装工艺中,根据轴径大小不同,一般要求轴承与轴之间有0.4~1.6 mm 的安装间隙[12],而在不少文献中轴承的支反力出现了负值[1-2],但轴的挠度值并没有超过轴承的安装间隙,说明此处轴承虽然脱空,但并没有触及轴承上沿,所以轴承支反力应为0,而不是负值。
本文使用多点弹性支撑模型对艉管后轴承等效支撑位置进行计算,并做如下改进:在轴承的下沿和上沿分别设置对地的单向受压弹簧,当轴段脱空且挠度值小于轴承安装间隙(0.5 mm)时,弹簧保持自由,轴承支反力为0,整个模型如图4所示。

图4 多点弹性支撑模型Fig.4 Model of multipoint elastic support
2.3 基于赫兹接触理论的轴承非线性刚度计算
法国船级社[13]对附加“ESA”弹性校中符号的船舶,提出在静态条件下可用赫兹接触理论计算轴承支反力。本文依据赫兹接触理论,结合有关刚度计算方法,直接计算出轴承单元的载荷-刚度曲线,并应用于后续的校中计算。
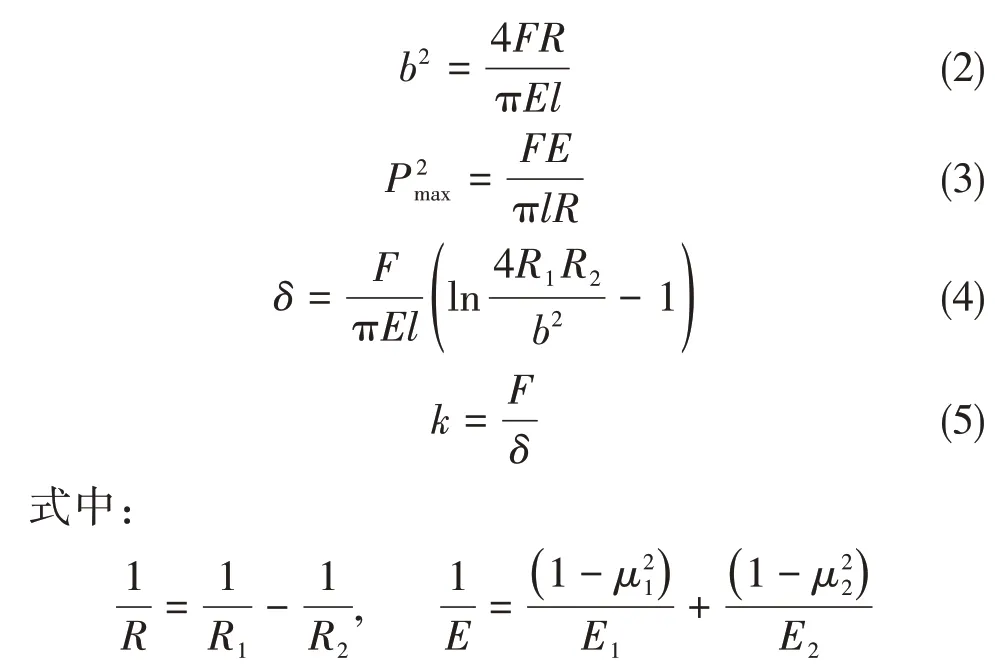
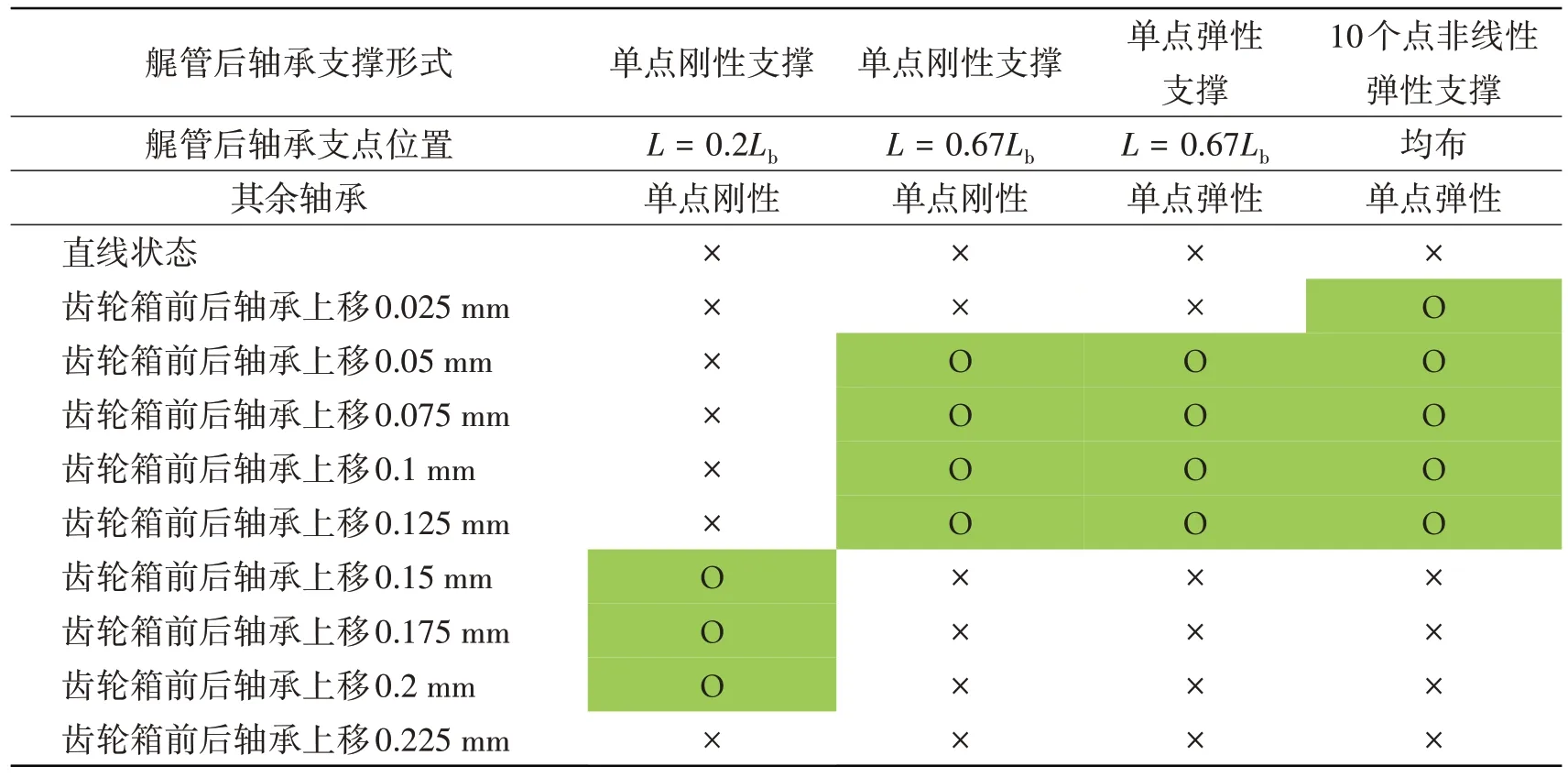
如图5 所示,两长度为l的平行圆柱内接,R1 图5 两平行圆柱内接Fig.5 Two parallel cylinders inscribed 图6 轴承单元的载荷-刚度曲线Fig.6 Load-stiffness curve of bearing unit 将上述刚度曲线应用到有限元模型,求得各轴承单元支反力和接触刚度,结果如图7和图8所示。其中,编号为③、④、⑤、⑥、⑦、⑧的轴承单元没有支反力,说明轴和轴承单元没有接触。将各刚度相加,得到艉管后轴承总接触刚度为3.8E+09 N/m,与文献[2,16]基本一致,同理可求得艉管前轴承总接触刚度约为2E+09 N/m。 本船齿轮箱大齿轮轴承为圆柱滚子轴承,同样使用赫兹接触理论结合式(5)可以计算出该圆柱滚子轴承的径向刚度[17]约为2E+09 N/m。将图7中各轴承单元负荷代入式(1),算得L=0.67Lb,即艉管后轴承等效支承点位置距该轴承后端面距离约为2/3轴承长度,符合本文第1章中有关支承点位置应位于艉管后轴承前半部分的判断。 为了检验单元体个数选取是否对等效支点的取值有影响,表3 列出了2 个、5 个、10 个、20 个单元的计算结果对比。结果显示,单元体个数选取5个以上即可获得较高的精度。 表3 不同单元体个数的支点位置Tab.3 Position of different elements 使用本文第1章的有限元模型,结合第2章的内容,分别对表4的几种情况进行静态校中计算,这里只对冷态进行验证,并对齿轮箱前、后轴承偏移相同的值进行求解。其中,艉管前轴承及齿轮箱前、后轴承均为单点支撑,支撑位置取轴承中点。单点弹性支撑时,艉管后轴承刚度取3.8E+09 N/m,艉管前轴承刚度取2E+09 N/m,齿轮箱轴承刚度取2E+09 N/m。10个点非线性弹性支撑刚度按图6选取。 表4 不同艉管后轴承支撑形式的校中结果Tab.4 Alignment results of different stern tube rear bearing support forms 表中“О”代表通过,“×”代表不通过,评判通过与否的标准[5]如下: (1)在静态下,所有轴承为正负荷,即不出现轴承脱空现象; (2)轴承负荷不小于相邻两跨距间所有重量总和的20%; (3)齿轮箱大齿轮前、后轴承负荷之差不超过两轴承之间轴段与大齿轮重量之和的20%。 从表4 中可以看出:①L=0.67Lb的解域和L=0.2Lb的解域没有重合区域,在L=0.2Lb时校中通过的轴承偏移取值,用在L=0.67Lb时则无法通过;②后面三种情况的解域则基本重合,说明在轴承支点选取正确的情况下,单点刚性支撑、单点弹性支撑、多点非线性弹性支撑三种模型的计算结果相差不大;③L=0.67Lb的解域大于L=0.2Lb的解域,能容纳较大的安装误差。 轴系静态校中计算中,艉管后轴承的等效支点位置取决于其前、后轴系的负荷分布。大型、超大型船舶一般采用大功率、低转速柴油机作为推进主机,并配以大直径轴系及超大、超重螺旋桨传递主机扭矩和螺旋桨推力,这时螺旋桨端的负荷大于前端,取L=(1/7~1/3)Lb是合理的。而中、小型船舶吃水较浅,螺旋桨直径小、转速快,导致螺旋桨端较轻,此时如果艉管前后轴承间距取得稍大,艉管后轴承等效支点距该轴承后端面的距离就将超出CB/Z 338-2005建议的(1/7~1/3)Lb。 实际上,轴承支点位置与轴的转速、螺旋桨设计、轴系具体布置、轴承润滑方式、所取轴承刚度都有关系,在静态和运转状态下也不相同。就本算例来说,艉轴前、后轴承之间轴的长径比为31,在其他条件不变的情况下,艉轴跨距缩短1.5 m,则艉管后轴承支点位于L=Lb/3,此时,艉轴前、后轴承之间轴的长径比为24。 本文基于有限元法,将轴系结构简化为Timoshenko 梁单元,建立了有限元模型,并使用不同支撑点位置和多种支撑模型对艉轴大跨距轴系进行了校中计算。同时,考虑船舶轴系实际安装间隙,使用单向受压的非线性弹簧代替常规的弹簧单元,并基于赫兹接触理论计算轴段的载荷-刚度曲线。通过对比分析,得到以下结论: (1)将艉管后轴承沿长度方向分成N个轴承单元后,每个分轴承单元刚度并不相等,而是与轴承载荷以及实际接触情况有关,单元体建议选取5个以上; (2)在轴承支点选取正确的情况下,单点刚性支承、单点弹性支承和多点非线性弹性支承三者的各轴承总负荷计算结果相差不大,但是多点非线性弹性支承模型不仅可以给出轴承各处负荷分布,并且同时解决了轴承支点位置选取问题; (3)对于艉轴大跨距的轴系(比如本算例中艉轴前后轴承之间轴的长径比大于24时),CB/Z 338-2005 中对艉管后轴承支点位置的取值已不适合,按其取值可能会导致轴系合理校中结果不合理。此时如找到合适的轴承支点位置,则其刚性支撑模型的校中计算结果也仍然符合轴系的真实情况。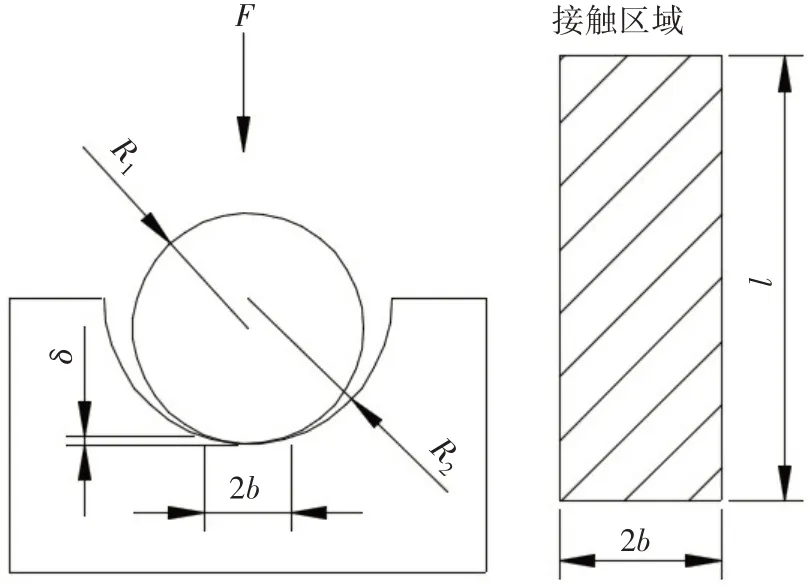

2.4 多点弹性支撑模型轴承单元负荷、刚度和等效支点位置计算

3 艉轴大跨距轴系校中
4 结 论
