声学黑洞加筋板结构的声振特性分析

2024-03-22温华兵黄惠文史自强郭俊华

船舶力学 2024年3期

温华兵，黄惠文，史自强，郭俊华

（江苏科技大学能源与动力学院，江苏镇江 212100）

0 引言

当前船舶进行声学结构设计的主要目的是降低船舶舱室内的噪声和振动水平。船舶内部的机械振动源工作时产生振动并传递到船舶平台结构，引起平台结构振动并向周围舱室辐射噪声，因此动力设备支撑平台结构是动力设备振动波传递的主要途径。由于机械噪声具有显著的低频强线谱特征，易引起船舶结构的低频弯曲振动并产生强的辐射噪声。因此，降低以船舶支撑平台结构为主的结构噪声传递，开展船舶支撑平台结构声学设计，是船舶低噪声设计的关键并具有重要意义。

声学黑洞（Acoustic Black Hole，ABH）通过对均匀的梁结构与板结构进行幂律剪裁而实现能量的聚集效应，使弯曲波的群速度与相速度进入ABH 后逐渐减小并变为零，以至于能量被困到尖端而不发生反射，使能量聚集在ABH的几何中心[1-2]，但在实际制造时ABH的一维截面存在截断厚度，形成非完美ABH[3-5]。

近年来，有大量的学者从不同角度研究ABH 结构的声辐射问题及其在不同领域的应用[6-9]。Conlon等[10]提出通过计算模态损耗因子量化阻尼对ABH 板声辐射以及振动损耗的贡献；Li等[11]揭示ABH板声辐射效率降低的物理机理以及ABH 板有效声辐射区域在不同频率下与跨音速边界的关系；Tang等[12]设计新型ABH结构与等刚度等质量的普通板在无阻尼的情况下进行对比，结果显示辐射声功率、振动水平显著下降，验证了ABH 效应在低频时也能被触发；对此，王小东等[13-15]对ABH 进行了应用研究，通过搭建ABH 与板或腔室的耦合系统模拟飞机舱内噪音，分析耦合系统的物理降噪机理，验证耦合系统中嵌入ABH 可以在不破坏原有结构功能时具有降噪能力；文献[16-19]为研究平板与管道结构的振动能量分布特性，从能量流的角度为控制结构振动提供参考；黄薇等[20]通过使用振动功率流的方法研究ABH 的能量聚集效应，通过有限元计算出的功率流传递路径图可以直观地显示振动弯曲波聚集在ABH的几何中心。

虽然上述研究成果都说明ABH 具有的能量聚集效应在控制结构振动和减少声辐射方面具有优越性，但大部分文献都没有考虑ABH 在加筋板结构中的应用及对整体结构减振降噪性能的影响。本文将ABH结构引入到加筋结构中，船舶加筋板(Stiffened Plate,SP)与ABH的组合结构既可提高ABH的承载能力又可实现普通SP 的轻量化设计，从而设计出声学黑洞加筋板(Acoustic Black Hole Stiffened Plate,ABH+SP)。基于ABH+SP、SP 的有限元计算结果，分析得到ABH 与加强筋对声辐射效应及振动能量传递特性的影响，揭示ABH 与加强筋这两种结构的耦合减振机理，验证ABH 具有能量聚集效应而使ABH+SP的降噪效果明显。

1 结构设计及声振原理

1.1 结构设计方案

ABH+SP 结构如图1 所示，在ABH 的几何中心敷设阻尼层（Damping Layer，DL），上层薄板由变厚度区域与均匀厚度区域组成，ABH 的截面厚度与其半径之间的表达式为h（x）=εxm+h0，由于现有的工艺无法实现完美ABH，因此结构存在着截断厚度h0。其中，薄板的长2a=1000 mm，宽b=500 mm，厚度h=4.7 mm；加强筋的高c=100 mm；ABH 的半径rABH=150 mm，幂律m=2，平滑度常数ε=0.2；DL 的厚度为0.3 mm，半径r0=75 mm。为验证ABH+SP的减振降噪特性，设置SP为参考结构，两种结构除构型不一，材料参数、几何参数均保持一致。

图1 两种结构的示意图Fig.1 Diagram of two structures

1.2 声辐射特性

以辐射声功率、均方速度以及声辐射效率作为结构的声辐射特性评价参数。

（1）辐射声功率级

式中：W为板结构辐射到半无限大空间中的声功率，W0为基准声功率10-12W。

（2）声辐射效率

式中：ρ和c分别是声介质的密度和声速，S是结构参与声辐射的有效面积，|v|为均方振速，其表达式为

1.3 振动能量分布及传递特性

（1）动能密度比

将动能密度比Γ定义为在ABH 区域的表面动能密度EABH与整个结构的表面动能密度Ep之比，表达式如下：

（2）功率流

结构声强借鉴了声学中声强的概念，可用于表示二维平板结构上某点能量的大小和方向，将弹性力学的相关理论融入到结构声强的理论中，得到用结构内部应力参数表达的结构声强：

式中：Nx、Ny分别为板上单位宽度的面内轴力；Nxy=Nyx为面内剪力；Qx、Qy分别为板上单位宽度上的横向剪力；Mx=My为板上单位宽度的弯矩；Mxy=Myx为扭矩；u̇*、v̇*、ẇ*分别为x、y、z方向上速度的复数共轭；θ̇*x、θ̇*y分别为绕x、y方向的转速的复数共轭。

1.4 声学黑洞的相关频率

探究ABH对结构声振特性的影响，引入ABH截止频率[21-22]、临界频率[10]的相关概念。ABH区域出现的第一阶局部模态称为截止频率f0，本文中f0为500.53 Hz；临界频率fc的表达式如式（6）所示，说明ABH的弯曲波波长与ABH半径大小紧密相关。

式中：E为弹性模量，ρ为密度，ν为泊松比，h为薄板厚度，rABH为ABH 的半径。计算得到ABH+SP 的fc为1005.6 Hz。

2 数值仿真模型

2.1 声辐射的有限元模型

本文使用COMSOL有限元仿真软件对ABH+SP进行声振特性计算，模型采用软件中的声-固耦合板块，在ABH+SP结构上方设置半径为750 mm的半球空气域，声学介质设置为空气（空气密度1.21 kg/m3，声速343 m/s），为保证计算的准确性，每个波长内至少有8个单元，有限元模型如图2（a）所示。板结构设为四边固支，单位简谐力激励位于左上角处点（50 mm，315 mm），具体材料参数如表1所示。

表1 声学黑洞加筋板的材料参数Tab.1 Material parameters of acoustic black hole stiffened plate

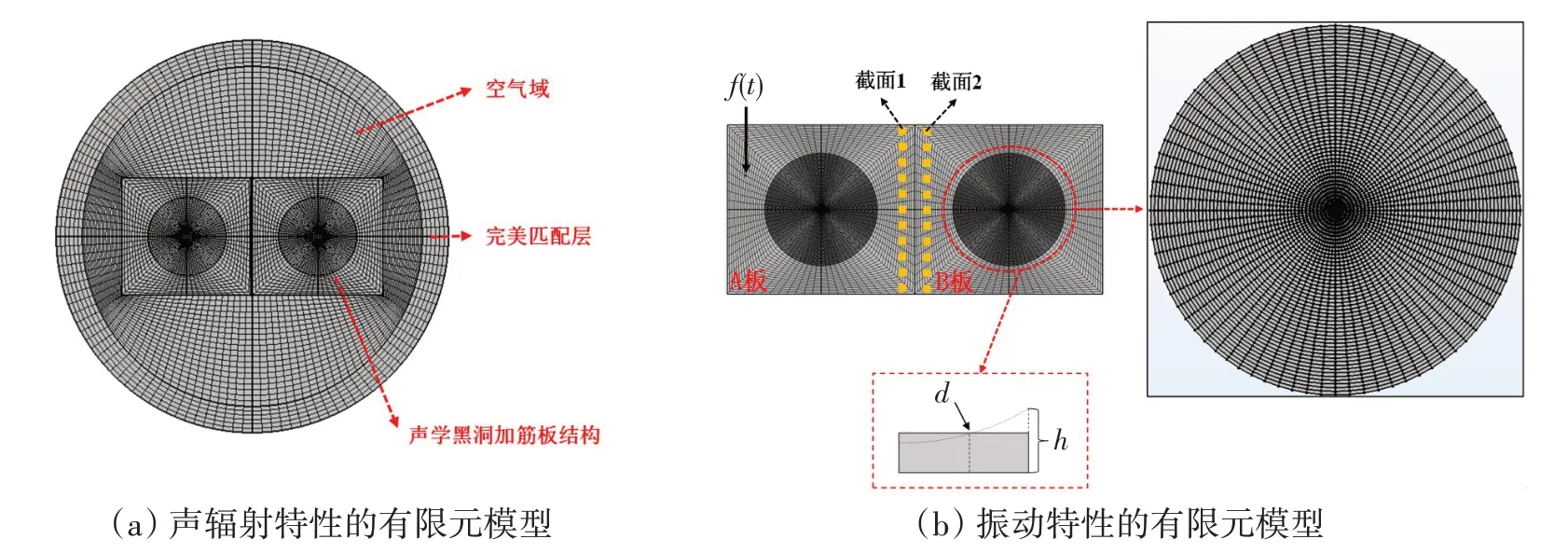
图2 声学黑洞加筋板的有限元模型Fig.2 Finite element model of acoustic black hole stiffened plate

2.2 振动特性的有限元模型

使用COMSOL 仿真软件的结构力学壳板模块对ABH+SP 进行振动特性计算，参数、边界条件均与声辐射计算保持一致。为了提取振动功率流幅值，对ABH 区域采用离散建模的方法，对ABH 中连续变化的截面进行离散化处理，离散为50份，厚度取左右边界的中点厚度值d。为了对比ABH+SP 的振动特性，将SP的有限元模型中与ABH 相对应的区域也离散成50份，其厚度均一致，有限元模型如图2（b）所示。

3 声学黑洞加筋板的减振降噪性能分析

3.1 降噪性能分析

如图3 所示，在低于f0频段内，ABH+SP 的辐射声功率级略大于SP，因为在板筋结构中内嵌ABH会导致结构的刚度下降，以致ABH+SP 在低频时降噪性能不佳。在f0～fc频段，ABH+SP 的辐射声功率级相较于SP 有较大下降，辐射声功率级的曲线呈现8～20 dB的降幅。在高于fc频段时，ABH+SP的峰值幅度开始系统性地整体降低，曲线峰值变得更为平滑。由于ABH 结构构造的特殊性使波速降低，波长变长，使本来向远场辐射的声波被抑制在ABH结构内部，导致大量的振动能汇集在ABH内，局部敷设的阻尼层再将汇聚的能量转化为热能。

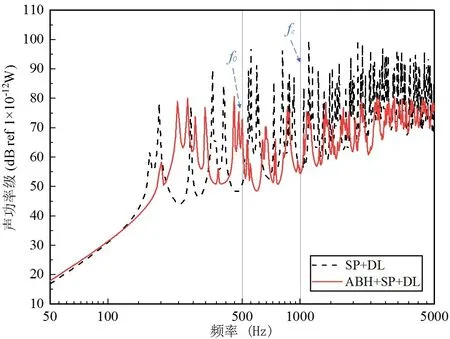
图3 结构的声辐射特性响应Fig.3 Acoustic radiation characteristic response of structure

采用均方速度、模态损耗因子、声辐射效率揭示ABH 实现降噪的物理机理。均方速度代表结构的振动水平，结构表面速度越大则声功率越大。由图4（a）可知，ABH+SP 的均方速度在绝大部分频段内低于SP，在高于fc频段时，ABH+SP的均方速度峰值减少且幅值显著下降。

图4 加筋板结构的振动响应特性Fig.4 Vibration response characteristics of stiffened plate structure

上述现象可通过图4（b）分析验证，在低于f0频段内，ABH+SP的模态损耗因子低于0.003，当高于f0频段时模态损耗因子开始显著增加，与SP 的模态损耗因子形成鲜明的对比。通过观察ABH+SP 在f0时的振型图，可以得知此时开始显现ABH 效应，AB 板的几何中心区域均存在着较高的振幅，敷设的局部DL开始发挥作用，使ABH+SP+DL 系统达到高效损耗的效果；在4789.9 Hz 时，ABH+SP 的模态损耗因子达到最高值0.019，观察其振型图可知，结构A 板、B 板的ABH 区域出现较为密集的局部共振，ABH 区域吸收大部分的动能再通过DL耗散。

声辐射效率代表结构与声场耦合的强弱，在等效面积下的均方速度与以活塞模式辐射的声功率比值[23]。本节采用声辐射效率来分析ABH 对声辐射特性的影响，分析图5 可得ABH+SP 的辐射效率在低于f0频段内高于SP，即使在振动水平较低的情况下仍与声场出现强耦合作用；在高于f0频段，声辐射效率开始降低，因为ABH+SP结构的ABH区域内出现高水平振动，减弱了整体板结构与声场耦合作用，使得声辐射效率降低。

图5 加筋板结构系统的声辐射效率Fig.5 Acoustic radiation efficiency of stiffened plate structural system

3.2 声学黑洞影响振动能量分布

图6 为ABH+SP 的AB 板区域的动能密度比曲线，在低于f0频段内呈现上升状态，随后其动能密度比曲线维持在5 dB 左右。根据公式（4）对动能密度比的定义，说明在高于f0频段时ABH发挥的集聚作用使AB板区域均保持着较高的动能密度比。由于SP结构无法对能量进行聚集，其振动能相对均匀分布在AB 板上，因此其动能密度比处于较低水平，曲线值远远低于ABH+SP。

图6 声学黑洞的能量聚集特性Fig.6 Energy aggregation performance of acoustic black hole

已知ABH+SP的B板的能量是经过加强筋阻振效应后传递的能量，但B板的动能密度比与A板的动能密度比数值大小相差无几，说明加强筋虽对部分能量的传递起到了能量阻挡作用，这并不会影响B板内嵌入的ABH在宽频下所具有的聚能作用。

为了更直观揭示两种结构振动能量分布特性，在低频选取500 Hz、高频选取4790 Hz这两个频率的动能密度云图与功率流流线图相结合进行分析，如图7所示。显然，在500 Hz时达到ABH的f0，ABH+SP的功率流流线指向ABH区域，说明能量开始流入ABH；SP的功率流的能量流线较为均匀分布在结构面板上，没有出现能量聚集效应。在4790 Hz时，ABH+SP的能量流线在ABH区域内形成许多小漩涡，流线漩涡代表所在区域有着高密度的能量，说明ABH区域内聚集着大量的能量，其动能密度最高达到0.12 J/m3；SP的高动能密度区域相对均匀分布在结构表面上，功率流流线所形成的旋涡区域与动能密度高的区域相对应。两种结构的振动能分布验证了ABH的能量聚集特性。

图7 加筋板结构的振动能量分布特性对比Fig.7 Comparison of vibrational energy distribution characteristics for stiffened plate structure

3.3 加强筋对振动传递特性的影响

如图2（b）所示，取加强筋左侧（A 板）截线的法向截面为截面1，加强筋右侧（B 板）截线的法向截面为截面2，两截面距离加强筋均为1 mm。通过对比截面1 与截面2 的功率流幅值曲线（如图8 所示），探讨加强筋对ABH+SP 的A 板、B 板振动传递特性的影响，参考功率流幅值取1×10-12W/m2。

图8 加强筋对振动传递响应的影响Fig.8 Effect of stiffener on vibration transmission response

在低于2000 Hz 频段时，截面1 与截面2 的功率流幅值相近，降幅不明显；在高于2000 Hz 频段时，截面2 的功率流幅值比截面1 下降了1～3 dB。虽然两个截面与加强筋的距离相近，截面2 的功率流幅值对比截面1 不会出现大幅下降，但是加强筋的存在仍阻挡了部分能量从A 板传递到B 板，验证了加强筋对能量传递具有阻振效应，也说明加强筋的存在可以使声学黑洞加筋板结构在中高频段具有较好的减振效果。