一次性条件下top-k高平均效用序列模式挖掘算法
2024-03-21杨克帅武优西刘靖宇
杨克帅,武优西*,耿 萌,刘靖宇,李 艳
(1.河北工业大学 人工智能与数据科学学院,天津 300401;2.河北工业大学 经济管理学院,天津 300401)
0 引言
序列模式挖掘(Sequential Pattern Mining,SPM)作为数据挖掘领域中重要课题,旨在从序列数据库[1]发现支持度(在序列数据库中出现次数)满足用户最小支持度阈值的子序列,被广泛应用于多种实际场景,如DNA 序列检测[2]、用户购买行为分析[3]和网页点击流挖掘[4-5]等。
传统频繁序列模式挖掘只考虑模式是否在序列中出现,而忽略了它在序列的出现次数。为解决此问题,重复挖掘方法[6-12]应运而生,该方法通过模式匹配技术计算模式在一条序列的出现次数。例如:假定有两个消费者,他们的购买次序分别形成了两条消费序列S1={(1,ab)(2,a)(3,abc)}和S2={(1,bd)(2,ab)(3,acd)(4,abc)(5,ac)(6,ac)(7,ab)(8,ad)(9,cd)}。以S1为例,它表示消费者1,第1 次购买了a 和b 两样商品;第2 次仅购买了a 商品;第3 次购买了a、b 和c 共三样商品。易知模式(ab)(c)在S1和S2中均有出现。由于传统的序列模式挖掘方法不甄别模式在序列中的重复性,因此模式(ab)(c)在S1和S2中的支持度为2。而可重复序列模式挖掘则甄别模式在序列中的重复性,易知模式(ab)(c)在S2中的出现了3 次,出现位置为因此在可重复序列模式挖掘中,模式(ab)(c)在S1和S2中的支持度分别为1 和3,总支持度为4。由此可见,消费者2 比消费者1 在模式(ab)(c)上具有更大的兴趣。因此,可重复序列模式挖掘与传统序列模式挖掘方法显著不同。
此外,与一次性条件[12]不同,文献[12]在单项序列上进行挖掘,即序列是由若干单项构成的,此研究的对应S1序列是{abaabc};而本文在通用性更强的项集序列上进行研究,问题更通用、更复杂。
更重要的,目前大部分重复挖掘算法都是基于模式的出现频率判断模式的重要程度,忽略了项本身的重要程度。实际上,生活中的序列通常包含大量的辅助信息,例如销售序列中商品的购买数与利润。如果忽略项目的价值将会导致一些出现频繁但用户不感兴趣的模式被发现。如商场商品中,面包的销量高于钻石,但钻石带给商家的利润远高于面包,因此,只依据出现频率判断模式的重要程度并不合理。为解决此问题,研究者们提出高效用序列模式挖掘,为序列中的项赋予权重[13-16](又称效用)用来表示各项的重要程度。除此之外,由于模式的效用由模式中各项效用累加得出,随着模式长度的增加而增加,导致较长的模式更容易成为高效用序列模式。为此,高平均效用序列模式挖掘[17]被提出,综合考虑模式的出现频率、各项的效用和模式长度,用于发现更符合用户需求的模式。如Wu 等[18]提出的HAOP-Miner(self-adaptive High-Average utility One-off sequential Pattern Miner)算法主要解决一次性条件下自适应高平均效用序列模式挖掘问题。HAOP-Miner 使用了用于计算模式支持度的Rf 算法,该算法采用逆序填充队列减少冗余节点。虽然该算法可以用于高平均效用序列模式挖掘,但它的挖掘对象为单项序列数据库,无法处理项集序列数据问题,并且它在先验知识不足的情况下很难给出恰当的平均效用阈值。
上述高平均效用序列模式挖掘需要用户提供最小平均效用阈值,然而在缺乏先验知识的前提下,很难选择合适的阈值。为此,top-k挖掘方法可在先验性不足的情况下得到用户所需数量的模式[19-21]。如Le 等[22]提出了top-k挖掘方式,用户只需提前给出想要挖掘的模式数,通过采用阈值攀升的方式挖掘用户最关注的k个模式;然而该算法仅根据支持度判断模式重要性存在不足。Zhang 等[20]提出了TKUS 算法,该算法采用投影和局部搜索机制,并采用了序列效用攀升、提前终止和消除冗余模式的策略,大幅减小了搜索空间;但该算法基于定量数据库挖掘top-k高效用模式,未考虑模式长度等因素,并只考虑了模式是否在序列中出现,没有计算在一条序列中的重复出现次数,导致一些重要的模式被忽略。综上所述,本文提出TOUP(Top-kOne-off high average Utility sequential Pattern mining)算法高效地挖掘一次性条件下用户最感兴趣的前k个高平均效用模式,可以根据阈值攀升的方式动态改变候选集和结果集,以达到最终挖掘出用户最关注的k个高平均效用模式的目标。
本文的主要工作如下:1)在支持度计算方面,提出基于各项出现位置与项重复关系数组的CSP(Calculation Support of Pattern)算法,以降低时间空间复杂度;2)在候选模式生成方面,提出基于最大平均效用上界的剪枝策略,以减少候选模式数;3)在多个真实数据集和合成数据集上验证了TOUP算法的有效性。
1 相关工作
SPM 自被提出以来,广泛应用于诸多领域[23-26],面对不同的挖掘需求,多种形式的SPM 被提出,如闭合模式挖掘[3]、最大模式挖掘[25]和负序列模式挖掘[26]等。传统SPM 只考虑序列中是否存在该模式,而不考虑它在序列中重复出现,但模式在少数序列中多次出现的信息同样重要。为解决此问题,文献[6-8,11]根据模式在序列中的重复使用情况,研究了无约束、无重叠和一次性条件下重复序列模式挖掘问题。
然而,仅考虑模式的出现频率无法满足现实需求,例如用户购买行为分析中,有些商品尽管销量很高,但带给商家的利润较低;而有些商品虽然销量很低,但所带来的利润很高。因此,需要采用效用[27-28]进行计算,高平均效用序列模式挖掘[29]通过综合考虑模式的支持度、效用和长度,挖掘数据集中平均效用值不小于最小平均效用阈值的模式。Segura-Delgado 等[17]提出了一种进化算法,用于从受平均效用和可解释性影响很好的纵向人类基因表达数据中挖掘生物相关的高平均效用序列规则;然而,模式的平均效用并不满足反单调性,给候选模式生成与剪枝问题带来很大的困难,为此,学者们提出了多种满足反单调性的上界,利用反单调性对候选模式进行剪枝,以提高算法效率。Kim 等[30]提出了最大平均效用上界和最大剩余平均效用上界,由此提出了基于列表的新数据结构,并由该数据结构提出了两个剪枝策略。然而,上述挖掘方法没有考虑模式在序列中的重复性问题,为此,Wu 等[18]在单项序列上研究了可重复高平均效用序列模式挖掘问题,在支持度计算方面通过逆序填充算法高效地获得模式在各条序列中的出现次数,在候选模式生成方面提出了支持度下界概念,并在此基础上使用模式连接策略减少候选模式数。
上述研究均在用户提供最小效用阈值的情况下进行挖掘,然而在没有足够的先验知识前提下,无法设计合理的阈值,将会导致过多或过少的模式被发现。鉴于此问题,top-k挖掘方式被提出,用于挖掘用户最感兴趣的k个模式。Le等[22]提出了top-k挖掘方式,用户只需提前给出想要挖掘模式数,通过采用阈值攀升的方式扫描候选集和结果集,使得最终只挖掘出用户最关注的k个模式。但该算法仅能在不确定数据库中挖掘频繁序列模式,无法解决项集序列数据库中挖掘高平均效用模式问题,且忽略了模式在序列中的重复出现。
综上所述,本文提出一次性条件下top-k高平均效用序列模式挖掘算法,与先前研究相比存在如下差异:
1)挖掘模式类型不同。与频繁序列模式挖掘不同,在考虑模式出现频率的基础上综合考虑各项效用与模式长度,挖掘用户更感兴趣的高平均效用模式。
2)支持度计算方式不同。与传统的只考虑模式是否出现的判别方式不同,使用模式匹配技术计算模式在序列中的具体出现次数,更好地表达用户的兴趣程度。
3)候选模式剪枝策略不同。提出满足反单调性的平均效用上界,在此基础上构建高效的候选模式生成策略与剪枝策略。
4)结果集选择方式不同。与预先设定最小阈值方式不同,采用top-k挖掘方法,在先验性不足的情况下,挖掘用户最感兴趣的k个高平均效用模式。
2 问题定义
序列数据库D由k条序列组成,记作D={S1,S2,…,Sk}。序列由n个项集组成,每个项集包含若干有序项,记作S=s1s2…sn,si⊆Σ(1 ≤i≤n),Σ表示数据库D的项目集[31]。如表1 所示,序列数据库D由2 条序列组成,项目集Σ={a,b,c,d},其中序列S1中第一个项集S1=(1,ab)。

表1 序列数据库DTab.1 Sequence database D
定义1模式[8]。大小为m的模式记作P=p1*p2*…*pm(或简写为P=p1p2…pm),其中*表示传统通配符,意味着任意数量的项集都可以在这里出现。模式P的长度为模式中所有项的数量,记作len(P)。给定模式P=(ab)(a)(c),模式长度len(P)=4。
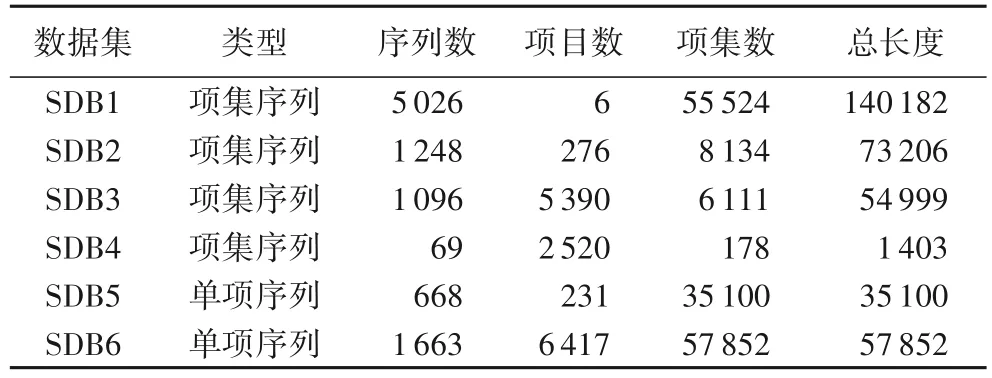
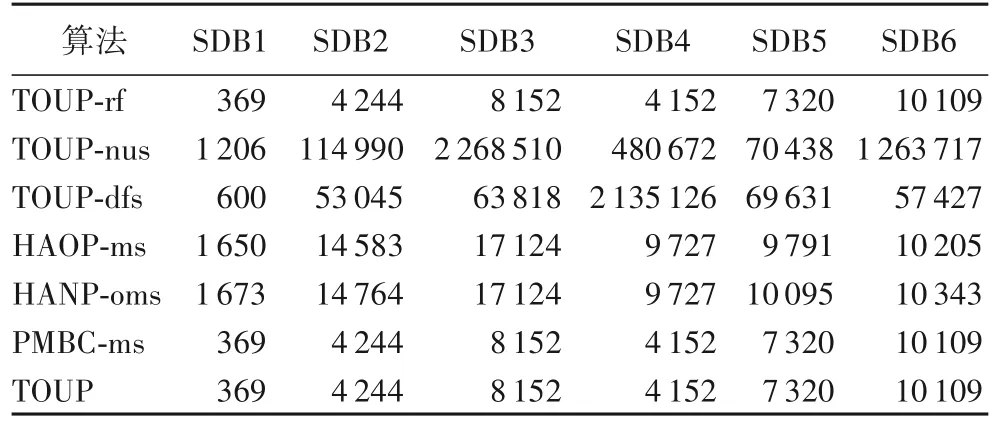
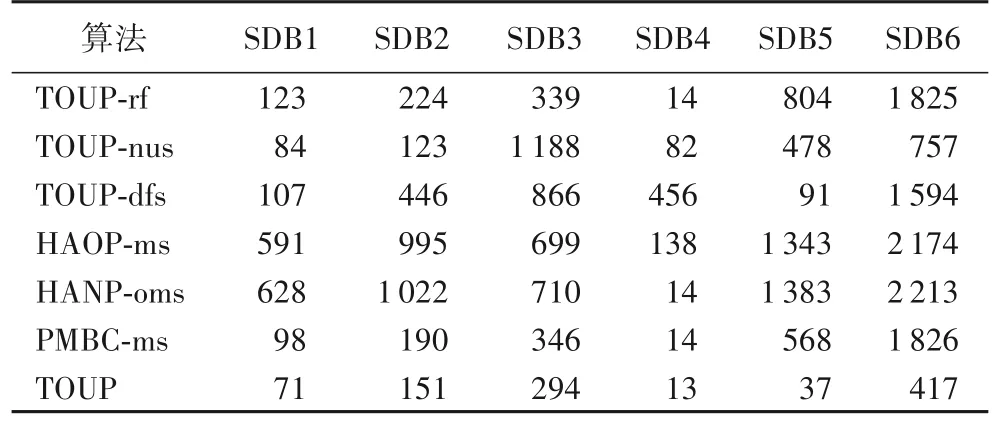
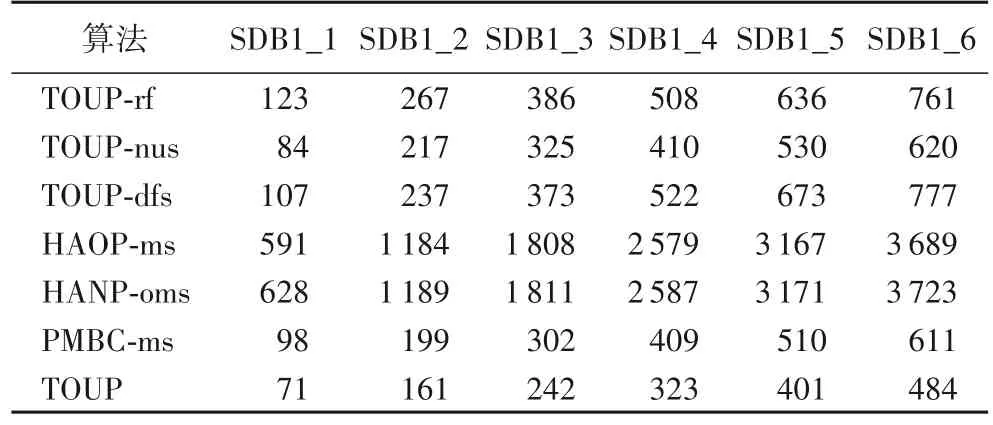
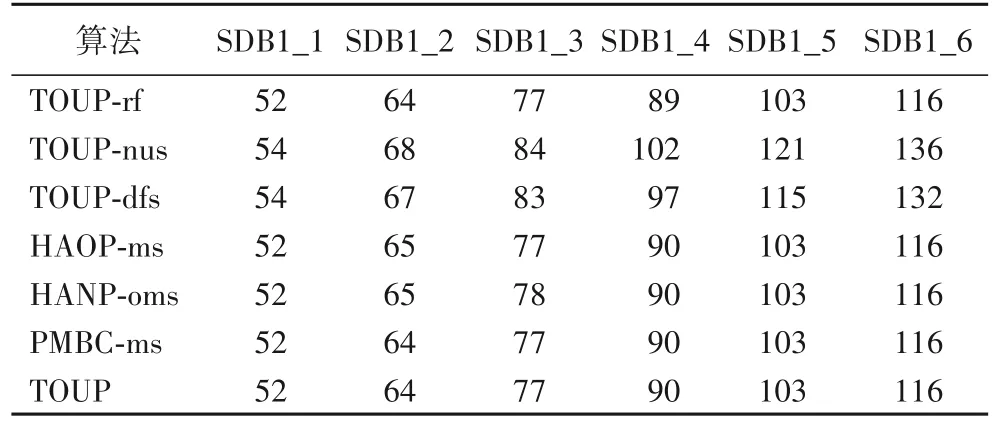
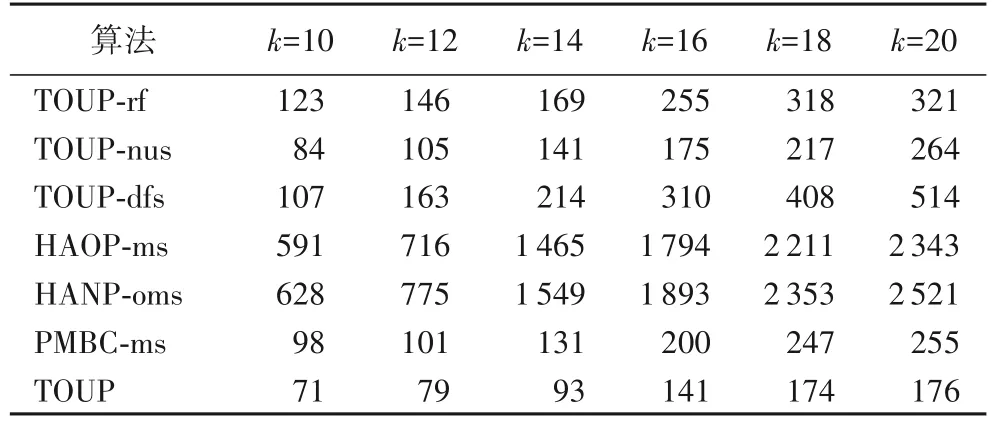
定义2出现和一次性出现。给定m个整数L=当且仅当1 ≤l1 定义3支持度。模式P在序列S中一次性出现数为P在S中的支持度,记作sup(P,S)。模式P在包含k条序列的序列数据库D中的支持度记作 例1 给定如表1 所示序列数据库D和模式P=(ab)(a)(c)。因 为p1=(ab) ⊆s1=(ab),p2=(a) ⊆s2=(a) 和p3=(c) ⊆s3=(abc),所以模式P在序列S1的一个出现,为同样P在S1中有很多出现,如和虽然两个出现中同时使用了位置3 但是在第一个出现中p3使用了s3中的项“c”,第二个出现中p1使用了s3中的项“a”和项“b”,并没有重复使用序列中相同的项。因此满足一次性条件,模式P在S1中有两个一次性出现。同理可求得P在S2中有两个一次性出现。所以P在序列数据库D中的支持度为 定义4效用与平均效用。 在带有效用的序列数据库中项目i的效用值记作u(i),模式P的效用为模式中所有项的效用之和与模式支持度的乘积,记为: 模式在序列数库中的平均效用为模式在数据库中的效用与模式长度的比值,记为: 其中:pk为模式P中的项集,ij为项集pk中的项。 例2 给定序列数据库D中各项的效用如表2 所示,项“a”和“b”的效用分别为10 和5。在例1 中,模式P的长度len(P)=4 和支持度sup(P,D)=4,所 以U(P,D)==4 ×((10+5)+8+10)=132,AU(P,D)=U(P,D)/len(P)=132/4=33。 表2 效用表Tab.2 Utility table 定义5top-k高平均效用模式。序列数据库中平均效用值最高的k个模式被称为top-k高平均效用模式。 问题陈述 预先给定序列数据库D,效用表T和用户定义的参数k,TOUP 的目标是找出top-k高平均效用模式。 为了挖掘top-k高平均效用模式,本文提出TOUP 算法,该算法包括平均效用计算和候选模式生成两部分。3.1 节介绍了模式平均效用计算的方法,首先统计模式P中各项在序列中的位置信息,然后直接通过项的出现位置和模式P中各项的重复关系计算出模式支持度,避免了对序列数据库的重复扫描,提高了计算效率。3.2 节介绍了候选模式生成策略,鉴于模式的平均效用不满足反单调性的情况,提出了最大平均效用上界,并基于Apriori-like 性质提出剪枝策略,有效减少了候选模式数。3.3 节中提出TOUP 算法,在挖掘过程中动态更新结果集与阈值,高效地发现用户最感兴趣的k个高平均效用模式。 根据式(2)可知,模式的平均效用计算的关键问题是支持度的计算。传统的支持度计算方法不考虑模式的重复出现次数,例如Srivastava 等[16]使用列表结构记录数据库中的模式发生情况和效用,但是列表结构只记录模式是否发生,很难处理重复挖掘问题。OWSP-Miner(self-adaptive One-off Weak-gap Strong Pattern mining)算 法[12]和HAOP-Miner 算法[18]虽然可以处理重复挖掘问题,但两者都是基于单项序列数据库的挖掘算法,无法直接计算项集序列模式的支持度。为了解决面向项集序列数据的重复挖掘问题,高效计算模式支持度,本节提出基于各项出现位置与项重复关系数组的CSP 算法快速计算模式支持度。CSP 算法通过以下4 个步骤实现每条序列中的支持度计算。 步骤1 创建m层节点,其中m是模式P的大小。第j层是位置数组Aj,存储了pj的位置信息。若pj只有一项,Aj存储该项的出现位置;否则Aj存储该项集内所有项的位置交集。 例3 给定模式P=(ab)*(a)*(c),通过遍历序列数据库可知,项“a”“b”和“c”在序列S1中的位置信息分别为:[1,2,3,4,5],[1,3,4]和[3,6]。由p1包含项“a”和项“b”,位置交集为[1,3,4],所以A1=[1,3,4]。同理,位置数组A2和A3分别为[1,2,3,4,5]和[3,6]。 步骤2 为了处理一次性条件,初始化模式中项重复关系数组R。 定义6项重复关系数组。大小为m的模式P的项重复关系数组中包含m个集合,第j个集合存储了模式P中与pj拥有相同项的项集所在位置。 例4 给定模式P=(ab)(a)(c),可知p1=(ab),p2=(a),则p1和p2拥有相同项,所以模式P的项重复关系数组R中第1个项集中存储了p2的位置号2,第2 个项集中存储了p1的位置号1,由于没有其他重复使用项,所以模式P的项重复关系数组R(P)=[[2][1][]]。 步骤3 在寻找一次性出现时,需根据项重复关系数组R判断该位置是否被使用。寻找第j层一次性出现位置时,判断该位置是否存在于R[j]。数组A1中查找未被使用的项作为当前节点e。然后重复以下操作:在下一层节点中查找未被使用的子节点c,使得c>e,直到寻找到第m层未被使用的子节点,至此该路径记作:L。 例5 根据数组R可知,第一层的第一个元素为1,由于该元素是第一层第一个元素,所以该元素一定满足一次性。寻找第二个项集的一次性出现位置,首先判断第二层第一个元素1,由于元素1 不大于第一层节点1,且根据数组R[2]=[1],第一层中的一次性出现位置为[1],即第二层第一个元素1 不满足一次性,删去第二层元素1。判断第二层第二个元素2,首先2>1,其次判断位置一次性,由于R[2]=[1],判断第一层中的一次性出现位置为[1],可知位置2 不在其中,所以位置2 满足一次性条件,所以节点1 在第二层的子节点为节点2。同理可知节点3 是节点2 在第三层的子节点。步骤3 结束,得到出现 步骤4 返回第一层继续重复步骤3,直到没有新的出现生成。 例6 继续扫描第一层中的元素,第二个元素是3,由数组R(P)=[[2][1][]]可知,p1和p2拥有重复元素“a”,在第一个出现中p2只使用了位置2,所以第一层第二个元素3 满足一次性条件。由步骤3 的第二层和第三层的一次性出现位置分别为4 和6。由于没有其他出现生成,步骤4 结束。CSP 算法的伪代码如下: 算法1 CSP 算法。 定理1CSP 算法的时间复杂度和空间复杂度分别为:O(nml)和O(ml),其中n、m和l分别代表数据库大小、序列大小和模式大小。 证明 CSP 算法在计算支持度时,首先扫描数据库中的各条序列,然后扫描序列以获得各项集的位置数组,根据位置数组计算模式的一次性条件出现频率。因此,CSP 算法的时间复杂度为O(nml)。CSP 算法主要内存消耗为模式的位置数组,最坏情况下,位置数组可当作一个m×l的多维数组,因此,CSP 算法的空间复杂度为O(ml)。 本节介绍了生成候选模式的模式扩展方法,为了减少候选模式数,提高算法的挖掘效率,提出满足反单调性的最大平均效用上界,并基于该上界提出剪枝策略对候选模式剪枝。 由于项集序列模式由若干项集构成,项集中包含一个或多个有序的项,因此,在生成项集序列候选模式时本文采用项集扩展(I-extension)和序列扩展(S-extension)的方法[32]。 项集扩展 在模式的最后一个项集内有序扩展新项。 序列扩展 在模式末尾添加一个新项集。 例7 给定模式P=(ab)*(a)*(c),项目集Σ={a,b,c,d}。根据项集扩展,模式P只能生成模式(ab)*a*(cd),这是因为项集中都是有序的项;根据序列扩展模式P可以生成模式(ab)*a*c*a、(ab)*a*c*b、(ab)*a*c*c 和(ab)*a*c*d。 虽然项集扩展和序列扩展不会丢失有效的候选模式,但是,模式的平均效用并不满足反单调性,如例8 所述。 例8 在例1 中已计算出模式P=(ab)*(a)*(c)在序列数据库中的支持度为4,即sup(P,D)=4。模式P'=(ab)*(c)是P的子模式,根据CSP 算法可得sup(P',D)=4。根据式(2),可知AU(P,D)=132/4=33 和AU(P',D)=92/3=30.7。尽管模式P'是模式P的子模式,但AU(P',D) 例8 说明了模式的平均效用不满足反单调性,无法直接使用Apriori 性质对候选模式剪枝,导致基于枚举树的候选模式生成方法生成指数级候选模式。因此,本文提出满足反单调性的最大平均效用上界,并基于该上界提出剪枝策略对候选模式剪枝。 定义7最大平均效用上界。 模式P在D的最大平均效用上界是它的支持度和项目集最大效用乘积,记为: 其中umax是项目集各项最大效用值。 例9 在例1 中模式P=(ab)*(a)*(c)在序列数据库D中支持度为4。根据表2 可知umax=u(a)=10,因 此maub(P,D)=4 × 10=40。 定理2最大平均效用上界模式满足反单调性。 证明 假设模式P'是模式P的子模式,L是序列S中模式P的出现。若序列S中模式P'的对应出现为L',则出现L'是L的子出现。因此,对于序列S中模式P'的每一个出现L',都可以得到对应的子出现L,表明序列S中模式P'的支持度不小于它的超模式支持度,即sup(P,S) ≤sup(P',S)。由于umax是常数,maub(P,D)=sup(P,D) ×umax不大于maub(P',D)=sup(P',D) ×umax,因此,最大平均效用上界满足反单调性。 定理3如果模式P的最大平均效用上界不大于最小平均效用阈值,即maub(P,D) ≤minau,则模式P的平均效用也不大于minau,即AU(P,D) ≤minau。 证明 因为umax是所有项的最大效用,所以P中每个项效用都不大于umax。由式(2)可知因此当maub(P,D) ≤minau时,AU(P,D) ≤minau。 剪枝策略 如果模式P的最大平均效用上界不大于minau,即maub(P,D) ≤minau,则模式P及其所有的超模式都可以被剪枝,其中minau是当前结果集中最小平均效用值。 例10 给定模式P=(ab)*(a)*(c),当前minau=50。由例9 可知maub(P,D)=4 × 10=40 本文提出TOUP 算法挖掘项集序列数据库下top-k高平均效用模式,具体步骤如下: 步骤1 根据式(2)计算每个项的平均效用,将平均效用排名前k的项存进结果集K,获得当前最小平均效用阈值minau,若项的个数不大于k,则初始化minau为零。 步骤2 根据式(3)计算各项的maub值,若maub>minau,则将该项存入队列C,并按照maub降序存储在数组I中。 步骤3 队列C中元素出队列记为模式P,基于数组I使用项集扩展和序列扩展生成模式P超模式集Q。 步骤4 从Q中取出模式P',分别根据式(2)和式(3)计算模式P'的au和maub,若maub(P',D) >minau,将模式P'储到队列C中,并当AU(P',D) >minau时,更新结果集K,minau和数组I;否则模式P'被修剪,直到Q为空。 步骤5 迭代步骤3~4,直到C为空,得到结果集K。 TOUP 算法的伪代码如下: 算法2 TOUP 算法。 输入 序列数据库D,效用表T,参数k; 定理4TOUP 算法的时间复杂度和空间复杂度分别为O(nmLt)和O(mL+t),其中n、m、L和t分别代表数据库大小、序列大小、最大模式大小和候选模式数。 证明 TOUP 算法的核心步骤为模式支持度计算,并且每个候选模式均需计算它的支持度。因此,TOUP 算法的时间复杂度为O(nmLt)。分析TOUP 算法可知,该算法主要内存消耗在于候选模式和支持度计算过程中位置数组的存储,因此,CSP 算法的空间复杂度为O(mL+t)。 为验证TOUP 算法的挖掘能力、可扩展性和不同参数对挖掘效率的影响,在真实数据集和合成数据集上对本文算法进行实验分析。 本文采用5 个真实数据集和1 个合成数据集验证TOUP算法效率,其中数据集SDB1(https://tianchi.aliyun.com/dataset/dataDetail?dataId=45)是一个婴儿产品的销售数据集;数据集SDB2(http://www.philippe-fournier-viger.com/spmf/datasets/_shop.txt)是网上购物点击流数据集;SDB3、SDB5 和SDB6 是真实数据集,SDB4 是合成数据集,来自http://www.philippe-fournier-viger.com/spmf/index.php?link=datasets.php。为了对比各算法在特殊序列数据库中的挖掘效率,SDB5 和SDB6 为单项序列数据库,其余为项集序列数据库。表3 是对所选数据集的介绍。 表3 实验数据集Tab.3 Experimental datasets 实验运行环境 操作系统为Ubuntu,处理器为Intel Xeon Silver 4210,主频为2.20 GHz,内存为64 GB,开发语言为Python,开发工具为PyCharm。 本文采用6 个对比实验验证TOUP 算法的有效性和可扩展性。其中TOUP-rf、TOUP-nus 和TOUP-dfs 共3 个对比算法用于消融实验,验证TOUP 算法各模块的有效性。并使用HAOP-ms、HANP-oms 和PMBC-ms 算法验证TOUP 算法挖掘的有效性。 TOUP-rf(TOUP-reverse fill)为了验证CSP 算法的有效性,提出TOUP-rf 算法,该算法采用文献[18]中提出的逆序填充策略计算模式支持度。 TOUP-nus(TOUP-no used itemset pruning strategy)为了验证剪枝策略的有效性,提出了TOUP-nus 算法,该算法在TOUP 算法的基础上未对长度为1 的模式进行剪枝。 TOUP-dfs(TOUP-depth first search)为了验证广度优先生成候选模式对挖掘效率的影响,提出了TOUP-dfs 算法,该算法使用深度优先生成候选模式。 HAOP-ms(HAOP-multiple itemsets)基于文献[18]中提出的HAOP-Miner 算法。 HANP-oms(HANP-one-off multiple itemsets)该算法基于文献[29]中提出的HANP-Miner(High average utility nonoverlapping sequential pattern mining)算法。 PMBC-ms(PMBC-multiple itemsets)基于文献[33]中提出 的PMBC(Pattern Mining from Biological sequences with wildcard Constraints)算法。 将上述算法用于解决一次性项集序列模式挖掘问题。 4.3.1 挖掘能力 本文在6 个数据集上,与对比算法TOUP-rf、TOUP-nus、TOUP-dfs、HAOP-ms、HANP-oms 和PMBC-ms 在生成候选模式数、运行时间和内存消耗上进行对比。其中预设k=10 和最小平均效用阈值minau=0,最小平均效用阈值在挖掘过程中攀升。表4~6 分别展示了TOUP 算法与各对比算法在候选模式数量、运行时间和内存消耗方面的对比。 表4 在6个数据集上不同算法生成候选模式数量对比Tab.4 Comparison of number of candidate patterns generated by different algorithms on six datasets 根据以上实验结果,可得出以下结论: 1)TOUP 算法中使用的支持度计算算法更加高效。TOUP-rf 算法采用逆序填充策略计算模式支持度,由表4、6可知,TOUP 算法与TOUP-rf 算法生成候选模式数量相等,两者内存消耗相似。但从表5 中可以看出,在运行时间方面TOUP 算法少于TOUP-rf 算法。如数据集SDB1 上TOUP 运行时间为71 s,而TOUP-rf 运行时间则为123 s,TOUP 运行时间效率提高了42.3%。这是因为它采用了基于各项出现位置与项重复关系数组的CSP 算法,能够快速搜索出现位置并判断是否满足一次性条件。因此,TOUP 算法优于TOUP-rf。 表5 在6个数据集上不同算法运行时间对比 单位:sTab.5 Comparison of running time among different algorithms on six datasets unit:s 表6 在6个数据集上不同算法内存消耗对比 单位:MBTab.6 Comparison of memory consumption among different algorithms on six datasets unit:MB 2)提前对1 长度模式进行剪枝可以有效提高算法挖掘效率。如表5、6 所示,TOUP 算法在运行时间和内存消耗方面均少于TOUP-nus 算法,这是因为剪枝策略能够有效减少可扩展项,在生成候选模式阶段避免一些冗余模式生成,从而降低算法的时间和空间消耗。例如在表4 中TOUP 算法和TOUP-nus 算法在SDB1 上的生成候选模式数量分别为369 和1 206,相较于TOUP-nus,TOUP 的候选模式数缩减了69.4%。因此对1 长度模式进行剪枝可以减少候选模式生成,从而有效地提高算法效率。 3)使用广度优先的方式生成候选模式可提高算法挖掘效率。与TOUP 算法不同,TOUP-dfs 算法使用深度优先遍历枚举树生成候选模式。由表4 可知,TOUP-dfs 算法生成了过多的候选模式,如在SDB3 中,TOUP 算法生成了8 152 个候选模式,而TOUP-dfs 算法却生成了63 818 个候选模式,TOUP算法的候选模式数降低了99.8%;在6 个数据集上,相较于TOUP-dfs 算法,TOUP 算法候选模式数降低了38.5%~99.8%。由于生成了较多的冗余候选模式,使得TOUP-dfs 算法有较长的运行时间,如表5 中TOUP-dfs 在SDB4 数据集上的运行时间为456 s,远高于TOUP 算法在SDB4 数据集上的运行时间13 s,所以TOUP 算法相较于TOUP-dfs 算法运行效率提高了97.1%;在6 个数据集上运行时间降低了33.6%~97.1%。造成这一现象的原因是深度遍历方式会优先生成较长的候选模式,而通常这种候选模式的平均效用值会很低。由此可见使用广度遍历生成候选模式可提高算法挖掘效率。 4)TOUP 算法相较于最新研究算法更加高效。如表5、6所示,TOUP 算法在运行时间和内存消耗方面均优于HAOP-ms、HANP-oms 和PMBC-ms 算法,因为TOUP 算法解决在项集序列数据库中挖掘一次性条件下top-k高平均效用序列模式的问题更加高效,生成了更少的候选模式。例如在表4 中TOUP 算法和HAOP-ms 算法在SDB1 上的生成候选模式数量分别为369 和1 650,所以TOUP 算法相较于HAOP-ms 算法,候选模式数缩减了77.6%;在6 个数据集上,TOUP 算法的候选模式数降低了0.9%~77.6%,运行时间降低了57.9%~97.2%。因此新提出的TOUP 算法拥有更高的挖掘效率。 综上,TOUP 算法在内存消耗、运行时间和候选模式数方面均优于其他对比算法。 4.3.2 可扩展性 为验证TOUP 算法的可扩展性,将数据集SDB1 扩展至原来的1~6 倍生成数据集SDB1_1、SDB1_2、SDB1_3、SDB1_4、SDB1_5 和SDB1_6。本节使用6 个对比算法在上述数据集上进行实验。预设k=10 和最小平均效用阈值minau=0。由于在倍数增长的数据集上各算法的候选模式数量大小不变,所以本节仅展现算法在各数据集上内存消耗和运行时间的对比。表7、8 分别展示了运行时间和内存消耗的实验结果。 表7 在SDB1_1~SDB1_6数据集上不同算法的运行时间对比 单位:sTab.7 Comparison of running time among different algorithms on SDB1_1-SDB1_6 datasets unit:s 表8 在SDB1_1~SDB1_6数据集上不同算法的内存消耗对比 单位:MBTab.8 Comparison of memory consumption among different algorithms on SDB1_1-SDB1_6 datasets unit:MB 随着数据集大小的增长,TOUP 的运行时间和内存消耗均在增加。由表7、8 可知当数据集从1 倍增加到6 倍时,运行时间增长了5.8 倍,内存消耗增长了1.2 倍。从以上数据分析,TOUP 挖掘效率和数据集大小呈正相关,且内存消耗的增长速度远低于数据集大小的增长速度。除此之外,根据表7、8 可以发现,在任意大小的数据集中,TOUP 算法的运行时间与内存消耗均低于其他对比算法。综上所述,TOUP 算法在大规模数据集具有较好的可扩展性。 4.3.3k值对实验结果的影响 为了验证在不同k值下,TOUP 算法相较于其他算法有更好的挖掘性能,使用6 个对比算法在SDB1 数据集上进行实验,将k值从10 递增到20。表9、10 分别展示了运行时间和候选模式数量对比。 表9 不同参数k的生成候选模式数对比Tab.9 Comparison of number of generated candidate patterns with different parameter k 由表9 可知,候选模式数量随着k值的增大而增大,如TOUP 算法在k=10 和k=20 时,候选模式数分别为369 和956。而更多的候选模式生成,导致更多的支持度计算次数,即更多的运行时间消耗,在表10 验证了这点:k值越大,运行时间越长。如TOUP 算法在k=10 和k=20 时,运行时间分别 为71 s 和176 s,增长了1.5 倍。而TOUP-rf、TOUP-nus、TOUP-dfs、HAOP-ms、HANP-oms 和PMBC-ms 算法在k=10 和k=20 时,运行时间分别增长了1.6 倍、2.1 倍、3.8 倍、3.0倍、3.0 倍和1.6 倍。综上所述,TOUP 算法挖掘效果更加高效。 表10 不同参数k的运行时间对比 单位:sTab.10 Comparison of running time with different parameter k unit:s 本文提出了在一次性条件下top-k高平均效用序列模式挖掘算法TOUP,该算法可以在不具备先验知识的情况下,挖掘用户最感兴趣的k个高平均效用模式。该算法主要包含平均效用计算与候选模式生成两个步骤。在平均效用计算方面,采用各项的出现位置信息与项重复关系数组实现高效的支持度计算,从而快速地计算模式的平均效用;在候选模式生成方面,采用项集扩展和序列扩展的模式扩展方式生成候选模式,并提出满足反单调性的最大平均效用上界,利用Apriori 性质剪枝冗余的候选模式,大幅减少了候选模式的生成数,提高了挖掘效率。本文实验部分通过与6 个对比算法进行对比,得出了TOUP 算法在候选模式生成、运行时间和内存消耗方面的性能均优于其他对比算法;还验证了TOUP算法具有较强的可扩展性,且它的挖掘性能受参数k值影响最小。综上所述,本文的实验结果均验证了TOUP 算法的高效性。 高平均效用序列模式挖掘的关键问题在于平均效用计算和候选模式生成,本文提出了通过位置信息和项重复关系数组的方式计算模式一次性出现与平均效用,使用基于最大平均效用的候选模式生成策略。但这样的挖掘方式太复杂,未来将研究如何减少扫描数据库次数,提高模式平均效用计算效率;研究更严格的上界与更优的剪枝策略。
3 算法描述
3.1 平均效用计算
3.2 候选模式生成
3.3 TOUP算法
4 实验与结果分析
4.1 数据集
4.2 对比算法
4.3 实验分析


5 结语
