三维桡骨成角楔形截骨术前自动规划算法

石志良，廖诗旗，甘梓博，祝少博

（1.武汉理工大学 机电工程学院，武汉 430070；2.武汉大学中南医院 骨科，武汉 430071）

0 引言

成角畸形是前臂骨畸形中一种常见的畸形类型。前臂骨折发生成角畸形时，改变了前臂固有的生理曲度，破坏了“旋前弓”和“旋后弓”，出现旋转过程中骨性阻挡或因成角畸形使骨间膜紧张，因而限制了前臂旋转活动［1］。目前，治疗成人前臂骨折的金标准是解剖复位、稳定的钢板固定和保护周围的血液供应［2］。为了达到精确治疗的目的，使用截骨矫形术可以有效矫正畸形、缓解疼痛、改善肢体功能和外观。然而，传统手动截骨矫形方法操作繁琐，矫正准确率低，因此，以自动化方式生成术前规划方案是截骨矫形手术的发展趋势。

手工交互截骨矫形分为二维手工截骨和三维（Three-Dimensional，3D）手工截骨。传统的二维（Two-Dimensional，2D）手术计划一般是利用前后视图、侧位视图的正交X 光片，由医生进行人工轴线绘制和角度测量，以确定畸形部位、截骨方式和截骨位置［3］。文献［4］中通过叠加两侧射线照片计算两个平面中最大变形面和真实畸变角度作为术前计划。这种依赖二维影像进行人工矫形的方法无法完全呈现三维解剖结构的真实情况，因此在畸形诊断上存在较大的限制。三维手工截骨矫形方法是在畸形骨与复位模板的近端或远端配准的基础上，对比畸形骨与健康骨的差异部分，根据医生临床经验选择合适位置进行截骨。文献［5-8］中提出了使用三维计算机辅助手工截骨矫形方法，这些方法通过三维重建技术使截骨矫正过程可视化，使医生能够更直观地了解规划过程，从而提升治疗效果和效率。但是，手工交互操作依赖于临床参数和规划者的经验，很难精准定位截骨位置，反复实验会浪费大量临床成本。

针对现有手动矫形方法存在的缺陷，研究人员提出利用几何计算与优化计算的方法自动生成术前规划方案。几何计算的方法通过畸形骨与对侧健康骨的远、近端配准变换矩阵解耦螺旋轴获取旋转角度，以解剖轴线的交点定义截骨位置进行截骨矫形。文献［9］中提出了一种基于几何计算的三维斜向单切旋转截骨矫形方法，目的是确定最佳截骨位置和截骨面平移量恢复旋转对齐；文献［10-11］中深入探讨了适用于不同类型长骨的三维术前自动截骨矫形规划方法，这些方法能够自动进行截骨位置和矫正角度的几何计算，同时考虑了临床上的限制因素。几何方法通常依赖于给定的几何规则和参数进行计算，对于复杂的非线性问题可能无法提供最优解，因此不能给出精确可行的术前规划方案。基于优化的方法根据临床约束和临床目标，对优化算法中的参数及目标区域进行约束，建立基于临床目标的数学模型，实现术前方案的自动生成。优化方法的优势是适用于各种问题，计算结果可以根据给定的目标函数和约束条件进行调整和改进，以找到最优解或接近最优解的解决方案。针对桡骨旋转截骨术，文献［12］中将畸形骨远端质心作为复位目标，使用单纯下降法对截骨位置与复位角度优化计算。文献［13］中采用斜向双切旋转截骨术，通过对骨长度、截面对齐等使用优化算法，将远端、中部和近端骨段与目标骨自动对齐矫正复杂的骨骼变形。这类方法提供了一种精确、简便且临床可用的术前规划方案，但均针对桡骨旋转成角混合畸形，不适用于成角畸形。针对桡骨旋转、成角楔形截骨术，文献［14-15］中提出了一种桡骨自动截骨矫形的算法框架，矫正复位取得了较好的效果；但方法需要同时将截骨切平面、骨碎片复位、固定板的位置、螺钉的方向和位置作为优化目标，导致优化方法涉及的参数较多，计算成本急剧增加。

此外，在计算机辅助三维规划手术中，健康对侧常被用作规划和评估的参考［16-17］。但是，大部分人使用惯用手更频繁，造成了上肢不对称。因此，文献［11］中提出人体双侧前臂长度差异可以通过对模型缩放进行补偿；文献［18］中提出应用线性回归模型描述桡骨和尺骨之间的双边差异，以纠正左右臂之间的长度差异；但这类用于补偿前臂长度差异的方法尚未应用于桡骨截骨矫形的自动规划问题。

在笔者的前期工作中，针对上肢畸形，提出了一种多阶段、多目标的加权优化方法，以解决截骨面、复位对齐、固定板和螺钉空间位置等多个问题［19］；对于上肢成角旋转混合畸形，利用遗传算法对上肢的复位对齐和骨接触面重叠率进行优化，实现了单刀斜切截骨矫形［20］；对于上肢成角畸形，采用拟牛顿法，通过确定截骨面和旋转角实现楔形截骨矫形［21］；拟牛顿法具有较好的收敛性，但存在计算复杂、易受初始点影响和易陷入局部极小值等问题。因此，本文采用内点算法，提出了一种解决上肢成角畸形问题的优化算法。

基于上述问题，针对桡骨成角畸形，本文提出一种桡骨楔形截骨矫形术前自动规划方法。首先，利用对侧镜像骨模型补偿差异后的模型作为矫形复位模板，通过迭代最近点（Iterative Closest Point，ICP）算法对桡骨近端和远端关节进行配准，自动计算畸形区域；其次，通过对桡骨远端关节的解剖区域进行加权配准，确定三维畸形轴的方向；随后，调整畸形骨使它与世界坐标系Y轴平行，并将畸形区域映射至XOZ平面，其中的畸形轮廓曲线采用三次样条插值法确定，从而确定复位旋转轴方位；最后，将关节解剖区域对齐作为截骨矫形的优化目标，以畸形区域为截骨平面约束、复位角的旋转范围为复位角约束，通过单目标优化算法进行迭代求解，自动生成最优的桡骨楔形截骨矫形术前规划方案。

1 楔形截骨矫形术前自动规划算法

1.1 算法流程

三维桡骨成角楔形截骨术前自动规划算法的总流程如图1 所示，具体步骤如下：

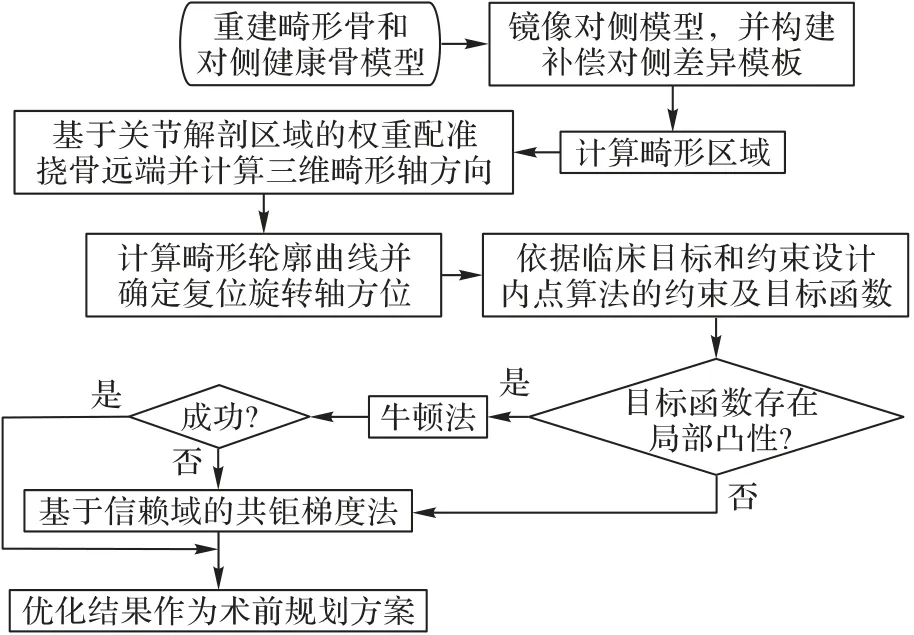
图1 算法流程Fig.1 Algorithm flow

1）将CT 数据进行三维重建，生成畸形和对侧健康桡、尺骨模型；

2）矢状面作为对称面，将对侧健康的骨模型进行镜像，随后将镜像得到的健康模型用作畸形骨矫形复位的模板；

3）采用迭代最近点配准算法对齐两侧桡骨和尺骨，计算两侧差异量并补偿，重建新的矫形复位模板作为参考骨；

4）计算畸形桡骨的畸形区域范围；

5）采用基于关节解剖区域权重的配准方法，计算桡骨三维畸形轴方向；

6）畸形骨变换至与世界坐标系Y轴平行，根据畸形区域范围计算畸形轮廓在XOZ平面的曲线及复位旋转轴方位；

7）畸形轮廓曲线上任取一点构建复位旋转轴，将畸形区域范围和复位旋转角度范围作为控制变量约束，以桡骨远端解剖区域配准均方根误差（Root Mean Square Error，RMSE）最小为目标设计目标函数，构建单目标优化模型；

8）优化迭代计算出最优的截骨平面和复位旋转角度，自动生成桡骨楔形截骨矫形术前规划方案。

1.2 补偿双侧差异

1）通过CT 数据创建畸形和健康侧桡骨和尺骨的三维三角形表面模型。

2）将三维世界坐标系中的XOZ平面作为对称平面，获取健康模型中每一个坐标点关于XOZ平面的对称点，根据点云数据生成对侧健康前臂的镜像模型。

3）采用双侧补偿的方法［18］纠正左右臂桡尺骨之间的长度差，提高术前规划的复位精度。具体步骤如下：

a）计算桡骨和尺骨模型的质心，并确定三条相互垂直的主轴线通过这两个质心。其中具有最小转动惯量的骨轴即为重力轴，对应桡骨的主旋转轴即桡骨长轴LR，对应尺骨的主旋转轴即尺骨长轴LU，如图2 所示。

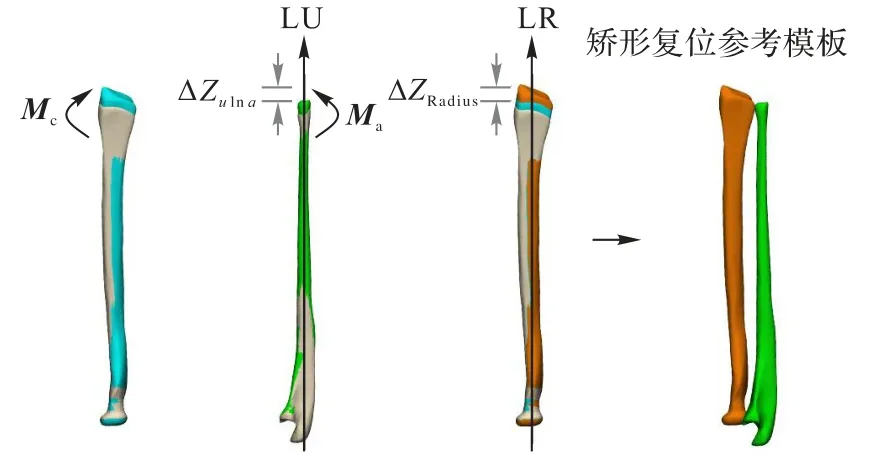
图2 补偿双侧差异Fig.2 Compensation for bilateral differences

b）桡骨近端和远端配准对齐得到矩阵Mpr和Mdr，由这两个矩阵可获得修正矩阵使桡骨远端相对于近端重新定位。同时，尺骨近端和远端配准对齐得到矩阵Mpu和Mdu，由这两个矩阵可获得补偿矩阵

c）由补偿矩阵Ma分解出平移矩阵，通过平移矩阵获取变换过程中沿XYZ三个轴的位移变换量，计算出沿重力轴的位移量ΔZUlna。

其中：C=0.98 是比例常数；ΔZRadius是沿桡骨轴所需的补偿半径；ΔZUlna是沿骨轴的位移量。

1.3 畸形区域

在优化过程中计算截骨位置时，采用一种畸形区域的自动计算方法［13］能够明确畸形骨偏离参考骨的具体位置，缩小搜索空间，同时减少计算量和时间成本。

1）利用ICP 算法对畸形及参考骨进行近、远端配准，计算两端的配准点集；

2）沿畸形骨模型的骨长轴将配准后的畸形骨模型和参考骨模型的点集以合适步长进行空间离散处理；

3）每一个步长内包含畸形骨模型和参考骨模型的点集，计算并搜寻畸形骨模型点集中每一点与参考骨模型点集中欧氏距离最小的点，通过计算每一个包围盒中的两个点集间的RMSE，衡量在此位置畸形骨与对侧镜像骨的偏离程度；

其中：PSD表示盒内畸形骨模型点集；PSN表示盒内参考骨模型点集；|PSD|表示集合PSD的基数。自动计算出的畸形函数图像如图3 所示。

图3 骨畸形函数Fig.3 Bone deformity function

4）根据外科医生建议，以偏离RMSE 最小值15%为畸形区域，计算畸形骨的畸形区域如图4 中所示。

图4 骨畸形区域Fig.4 Area of bone deformity

1.4 三维畸形轴

1.4.1 基于权重的关节局部区域配准

在临床上，桡骨远端由于与腕关节及尺骨远端关节相连，它的关节面的对齐比长骨区域的对齐更重要。因此，采用基于权重的关节解剖区域配准方法［13］对畸形骨与参考骨远端的标记区域进行精准复位对齐，以减小粗略对齐产生的误差。

1）在远端关节解剖区域选取7 个解剖点，并对7 个解剖点确定的解剖区域设置不同权重，权重取值范围为［0，1］，具体分配情况见表1。

表1 解剖点序号对应解剖位置名称及权重值Tab.1 Anatomic point serial number and corresponding anatomic position name and weight value

2）采用KDtree 算法［22］在7 个解剖点邻域内搜索50 个点。ICP 配准的评价指标［23］：待配准点集与参考点集之间经过矩阵变换后，点集数据之间满足某种度量准则下的最优匹配，即平均距离差值最小。因此，提出一种基于区域权重的点云配准误差评价指标如下：其中：K表示桡骨远端解剖区域的总数；N=50 为最邻近点对个数；wi表示各个解剖区域的权重值；R表示从畸形骨解剖点集变换至参考骨解剖点集的旋转矩阵；pij表示畸形骨解剖区域i中的第j个最近点，qij表示参考骨镜像模型解剖区域i中的第j个最近点。

1.4.2 三维畸形轴方向

1）畸形骨和参考骨远端通过关节整体区域配准，获得变换矩阵Md；畸形骨和参考骨近端通过基于权重的关节局部区域配准，获得变换矩阵Mp，由两个变换矩阵产生校正矩阵

2）Mc矩阵包括平移和旋转矩阵，从其中提取出不包含平移的矩阵R。

3）由矩阵R分解出3D 畸形轴的方向向量k［9］，如图5 所示，计算方法如下：

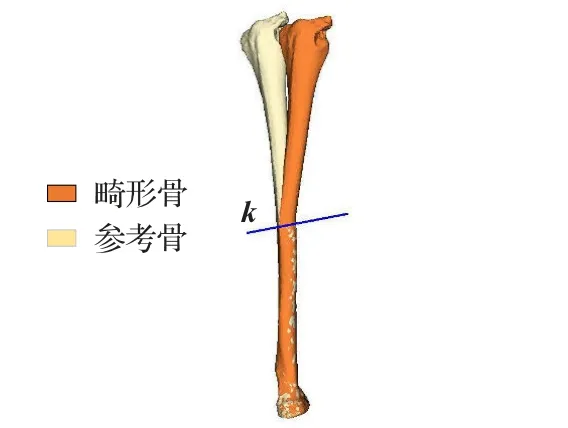
图5 3D畸形轴Fig.5 3D axis of malformation

1.5 畸形轮廓曲线和复位旋转轴方位

1.5.1 旋转轴方向向量

确定畸形轴的方向，构建同向的单位向量并进行变换，具体步骤如下：

1）以世界坐标系原点为起点，构建与三维畸形轴方向相同的单位向量V，并将单位向量V变换至与世界坐标系Y轴平行，即V=(0，1，0)；

2）计算方向向量V变换到与世界坐标系Y轴平行的变换矩阵MY；

3）对畸形骨及参考骨作MY变换，使其与Y轴平行，将畸形骨的畸形区域轮廓投影到XOZ平面，通过三次样条插值求解畸形轮廓曲线函数表达式。

1.5.2 畸形轮廓曲线

通过投影到XOZ面的畸形区域轮廓范围计算截骨平面的最近位置zmin和最远位置zmax。对畸形区域分段三次样条插值，其中两个端点为z0=zmin，zn=zmax，选取合适步长将区间[zmin，zmax]分成n个区间，畸形轮廓线在X轴上的极值点xmin、xmax作为旋转点的备选点，一侧控制开放楔形截骨，一侧控制闭合楔形截骨。计算过程如下：

在每一个小区间(zi-1，zi)(i=1，2，…，n)内，S(z)分别为三次多项式函数：

将数据节点和指定的首尾端点条件代入矩阵方程求解可得样条曲线系数ai、bi、ci、di，即可计算出曲线方程S1(z)，曲线方程S2(z)。畸形轮廓曲线图如图6 所示。

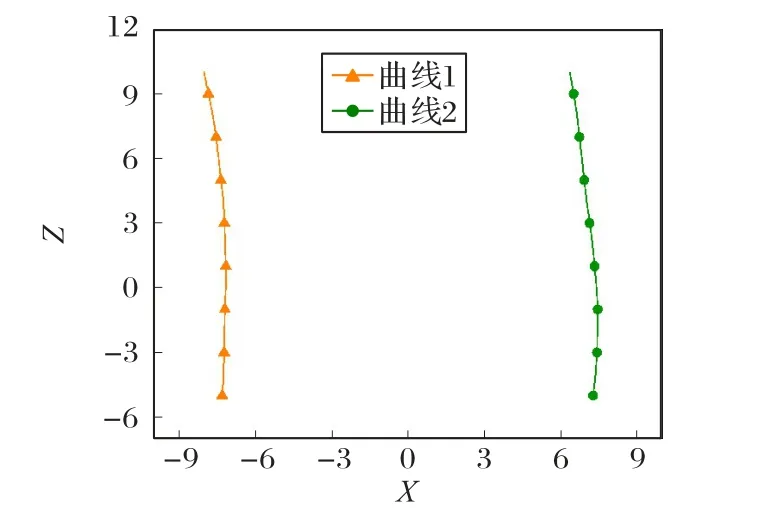
图6 畸形轮廓曲线Fig.6 Deformity contour curve

1.5.3 复位旋转轴方位

以畸形轮廓曲线上任意一点(S(z)，0，z)作为复位旋转轴位置，以旋转轴方向V=(0，1，0)作为复位旋转轴方向，确定复位旋转轴方位，其中S(z) ∈[zmin，zmax]。

1.6 优化方法

采用内点算法将惩罚函数定义在可行域内，并从可行域内某一初始点出发，在可行域内进行迭代。该算法的优势在于通过构造惩罚函数，将原有不等式约束优化问题转化为一个在定义域内的无约束非线性规划优化问题，结合牛顿法和基于信赖域法的共轭梯度方法进行求解。手动选取截骨位置及复位角计算繁琐，且找到最优方案较为复杂，自动计算的截骨位置不佳无法确定截骨方式，因此通过内点算法进行最优解计算。以桡骨远端解剖区域配准RMSE 最小为复位目标，畸形区域作为初始点的可行区域，轮廓曲线上任一点作为旋转轴位置参数，桡骨远端关节绕复位旋转轴旋转的角度为复位角参数，通过建立基于截骨平面位置和复位角变化的控制变量约束设计目标函数，利用边界和约束条件控制算法的搜索空间，优化迭代计算出最优的截骨位置参数和复位角参数，达到最优的远端关节解剖区域配准精度，自动生成桡骨楔形截骨矫形术前规划。

1.6.1 变量约束

变量约束包括截骨位置约束和复位旋转轴旋转的角度约束。

截骨位置约束是指在截骨过程中截骨平面可变化的范围。截骨平面决定截骨的大小和位置以及截骨的方向，不同的截骨位置会导致复位误差不同。优化开始前，通过骨畸形自动诊断确定截骨平面大致范围，即为截骨平面位置约束。

复位旋转轴旋转的角度约束是远端骨段绕复位旋转轴旋转至与参考骨模型远端的解剖区域对齐，即为复位旋转轴旋转的角度约束。旋转的角度θ变化范围为(-45°，45°)。

1.6.2 目标函数

桡骨成角畸形截骨术的术前优化目标为桡骨远端的关节局部区域配准RMSE，用于测量配准精度，精细控制复位对齐。具体描述如下：

桡骨远端关节解剖区域的配准精度：

其中：K表示解剖特征区域总数；wi表示权重，分配比例如表1；p表示畸形骨解剖区域的点，q表示重建模板解剖区域的点；f是畸形骨标志区域所有点pj与复位模板标志区域的点qj之间的欧氏距离的加权RMSE 值；R是将畸形骨的远端骨段旋转到正确解剖位置的变换矩阵。R的具体计算如下：

其中：T1表示将复位旋转轴平移到坐标原点的平移矩阵，T2表示T1的逆变换，R(θ)表示将复位旋转轴绕世界坐标系Y轴旋转θ角度的旋转矩阵。

1.6.3 内点算法

将实际问题转化为算法求解的形式，具体步骤如下：

1）建立数学模型。式（13）为目标函数，式（14）为不等式约束集合：

2）引入松弛因子，构造对数障碍函数作为惩罚函数，生成等价于原模型的优化问题，并将不等式约束问题转化为等式约束问题。

其中：r()k(k=0，1，2，…)为惩罚因子，是递减的正数序列；r(k-1)=r(k)c，c为递减系数；si≥0(i=1，2，3，4)为松弛因子。

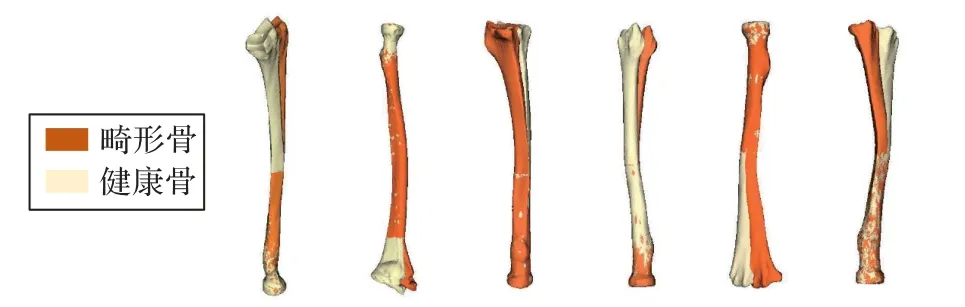
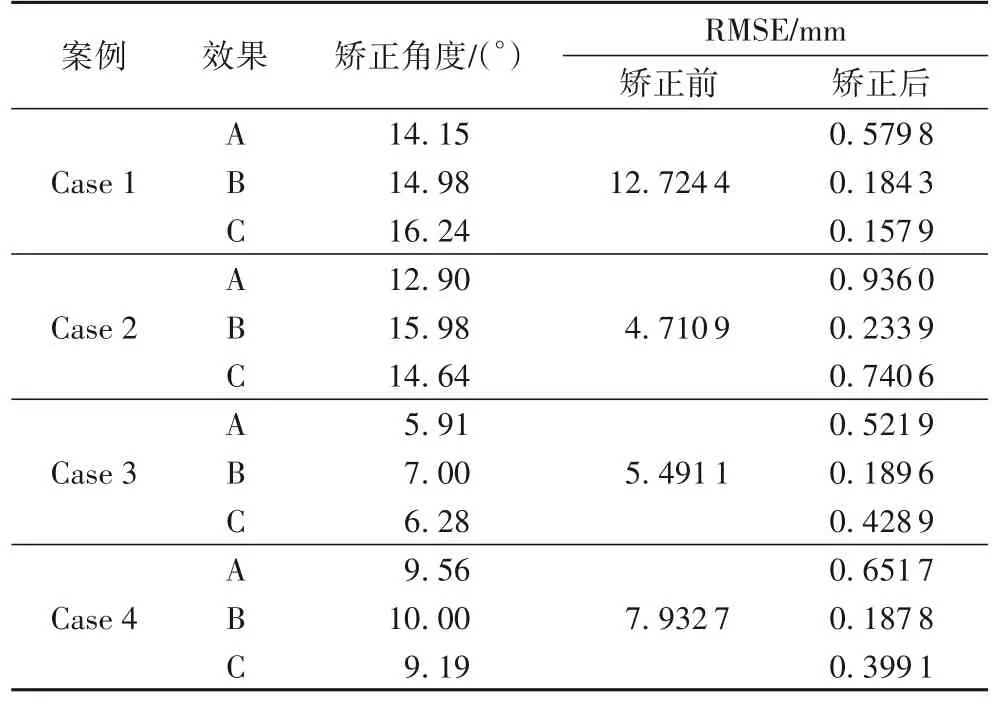
3）在定义域内任取初始点x(0)，初始惩罚因子r(0)>0，0.1

4）构造拉格朗日函数，处理等式约束。

其中：Fr(z，θ，s)是目标函数的逼近问题；λj(j=1，2，3，4)为拉格朗日乘数；H为拉格朗日函数的Hessian 矩阵。

5）利用迭代法求解库恩塔克条件（式（17）），获得最优点。

求解过程中，当拉格朗日函数的Hessian 矩阵正定时，目标函数在迭代点附近邻域内是严格凸函数，算法采用牛顿法。当Hessian 矩阵半正定时，目标函数在迭代点附近邻域内是凹函数，牛顿法失效，算法转为基于信赖域的共轭梯度法求解。逼近问题（15）在迭代附近不是局部凸时，直接采用基于信赖域的共轭梯度法。

6）若‖x∗(r(k))-x∗(r(k-1)) ‖≤ε或达到迭代次数，则终止迭代；否则令构造新的等式约束优化问题，转3）。

优化迭代后，求解结果即为术前规划的最优解，桡骨远端畸形骨段在最优截骨位置绕复位旋转轴进行旋转复位，旋转角度为优化计算的最优复位角。

2 实验与结果分析

2.1 实验数据集及环境

实验数据为6 例一侧畸形、对侧健康的患者桡骨CT，来源于武汉大学中南医院。图像层内间距0.78 mm，层间间距1.25 mm，图像强度单位为HU，对骨骼CT 进行重建处理重建后的三维模型格式为STL。

基于Windows 10 系统，采用Visual Studio 2019 开发平台，配置VTK8.2.0，PCL1.11.0 及QT5.14.0，开发出三维截骨自动规划原型系统，具有模型配准、切割及变换、骨畸形区域自动计算、桡骨成角畸形自动截骨矫形等功能。实验计算机硬件配置为Intel Core i7-9700F CPU @3.70 GHz，16 GB内存。

2.2 复位精度评估

选取6 例畸形桡骨模型，如图7 所示。算法验证组设置内点算法的初始惩罚因子大小r0=1，惩罚因子的缩小系数c=0.5，精度ε=10-4，迭代次数为200，通过系统自动计算最优的截骨位置及最优的复位角。

图7 畸形骨与对侧镜像健康骨原始模型Fig.7 Original model of deformed bone and contralateral mirror healthy bone

使用Miyake 等［6］提出的上肢畸形愈合骨折的三维截骨方法作为手动规划实验对照组。该方法对桡骨远端和远端关节整体配准对齐，计算畸形轴，医师根据经验在适当部位实施截骨术。畸形轴沿凹侧时，手动选择两个截骨平面切除楔形物，使远端骨段绕畸形轴旋转完成闭合楔形截骨术。畸形轴沿凸侧时，手动选择截骨平面，切开楔形骨完成开放楔形截骨术。

使用文献［11］中提出的楔形三维截骨方法作为自动规划实验对照组。该方法对前臂畸形骨与远、近端复位模板进行配准，解耦配准后的变换矩阵，获取畸形轴位置及矫形角度，以畸形轴位置作为截骨平面位置，将切割后的远端骨段自动绕畸形轴旋转所需角度，以实现矫正。

传统上，畸形根据比较量化，可与健康的对侧进行比较，因此，计算算法验证组和实验对照组中每一例畸形矫正后的远端关节解剖区域配准精度误差，如表2、3 所示。

表2 开放楔形关节解剖区域配准RMSETab.2 RMSE of anatomical area registration of open wedge joint

表3 闭合楔形关节解剖区域配准RMSETab.3 RMSE of anatomical area registration of closed wedge joint

图8 是6 例畸形桡骨实例矫正效果对比，Case 1～Case 4为开放楔形截骨，Case 5～Case 6 为闭合楔形截骨。其中：A表示手工规划组复位效果，B 为自动规划对照组复位效果，C为本文算法的复位效果，D 为手工规划组的截骨位置及矫正角度大小效果，E 为自动规划组的截骨位置及矫正角度大小效果，F 为本文算法的截骨位置及矫正角度大小效果。

图8 三维规划实例图Fig.8 Examples of 3D planning

由表2、3 可知，与手工规划相比，每一例畸形骨的自动规划误差均小于手工规划误差，并且自动规划的关节解剖区域配准RMSE 比手工规划降低0.093 0～0.421 9 mm，平均降低0.211 4 mm，结果表明自动规划的复位精度矫正效果均优于手动规划。与自动规划组相比，Case 1 中本文算法复位精度优于自动规划组，而Case 2～Case 6 自动规划组复位精度优于本文算法。

由图8 分析可知，Case 2～Case 6 中，自动规划组计算的旋转轴远离皮质骨边缘，矫正后的骨头无法明确定义楔形类型，部分重叠部分张开，如图8 中E2～E6，这种情况可以在术前规划时进行模拟，但在临床上不可行，因为旋转轴离皮质骨边缘过远，骨头并未完全切断，因此截骨后的远端骨段无法绕剩余骨桥进行旋转。本文算法计算的旋转轴位置均处于畸形骨皮质骨表面轮廓上，在截骨复位的过程中避免了截骨处的嵌合，因此能在满足临床要求的前提下，明确定义开放楔形和闭合楔形截骨方式，并精准复位。如图8 中F1～F4可直观看出为开式楔形截骨，F5～F6 为闭式楔形截骨。Case 1 中，自动规划组计算的复位旋转轴位置离皮质骨边缘较近，此时矫正的部分出现重叠范围较小，如E1，此时可以明确定义为开放楔形并进行矫正复位，但是它的复位精度低于本文算法。

图9 为复位旋转轴位置示意图。

图9 复位旋转轴位置示意图Fig.9 Position diagram of reset rotation axis

综上，根据实验结果可知本文算法复位精度及可行性更高。

3 结语

针对桡骨成角畸形，本文提出了一种三维楔形截骨矫形自动规划方法。选择6 例成角畸形矫形案例，与医生手动截骨矫形进行了对比分析，并通过桡骨远端关节解剖区域配准RMSE 大小验证。根据实验数据结果可知：本文算法相较于手动规划，复位精度更高；与自动规划方法相比，本文算法可明确楔形类型，且临床可行性更高。本文算法的局限在于，依赖于获取患者整个前臂双侧的CT 扫描，可能导致额外的CT 辐射暴露；依赖于骨骼解剖，忽略了术前规划中软组织缺失的影响。对于未来的研究，首先考虑健康的对侧无法参与规划的情况，预测畸形骨未受影响部分的正常形状；其次考虑术前过程中软组织的影响从而实现更复杂的模拟规划。