风力发电机组高强度螺栓的疲劳预测
2024-03-20郑启山朱少红陈长红常海青晏锡忠魏晨曦
郑启山,朱少红,陈长红,常海青,晏锡忠,魏晨曦
(1.福建国电风力发电有限公司,福建 福州 350014;2.厦门理工学院,福建 厦门 361024)
0 引言
风力发电机组塔筒各段连接处、主轴法兰与轮毂法兰之间、叶根与轮毂之间通常采用高强度螺栓进行连接,螺栓的工作状态直接影响着风电机组整体的运行安全[1]。在风力发电机组的设计寿命中,服役螺栓所承受的交变载荷次数高达109次,这些交变载荷的作用会使螺栓产生不同程度的疲劳,当螺栓疲劳损伤累积到一定程度时就会造成螺栓的失效[2]。在我国近几十年风电机组倒塌事故中,螺栓失效引发的事故占比最多[3]。因此,对螺栓疲劳损伤的评估和预测具有重要的工程意义。
目前对于风电机组高强度螺栓的疲劳寿命评估的主流方法有实验法、工程算法和有限元分析法。工程算法主要有Petersen 算法、VDI2230 算法和Schmidt-Neuper算法。Petersen 算法的关键贡献在于提出了螺栓疲劳等级S-N 曲线;VDI2230 算法局限性较高,主要用于解决结构简单的线性问题[4];Schmidt-Neuper 算法在工程上多用来处理结构强度和寿命的问题[5]。龙凯等学者均采用Schmidt-Neuper 算法模型,对风力机塔筒连接螺栓的疲劳累计损伤进行研究和分析[6]。梁原等人采用Schmidt-Neuper 算法与有限元分析法相结合的方法,分析了螺栓预紧力对疲劳累计损伤的影响规律[7]。欧阳卿采用两种S-N 曲线法估算了高强度螺栓的疲劳寿命,并在等寿命曲线的基础上,考虑了应力幅值和应力比的影响,推导出了螺栓疲劳设计公式[8]。何玉林等人对比了工程算法和有限元分析法的计算复杂度,验证了相对于有限元分析法,工程算法更为简单快捷且结果更为稳定,更适用于用来分析结构复杂的风机塔筒螺栓的疲劳[9]。
影响螺栓疲劳的因素有很多,如螺栓材料、螺栓预紧力、交变载荷等,其中轴向载荷是导致螺栓疲劳的主要因素[10]。风机塔筒连接螺栓的轴向应力循环次数通常大于104,属于高周疲劳范畴[11]。对于这种处于高周疲劳范畴的螺栓疲劳寿命的预测,通常采用德国学者Wohler 所提出的以S-N 疲劳寿命曲线和Miner 累计损伤理论为基础的名义应力法[12]。杜静等人基于有限元建模获取螺栓应力谱,再采用S-N 曲线、Miner 理论和MSC.Fatigue 软件相结合的方法,对塔筒法兰盘连接螺栓进行疲劳寿命分析[13]。鉴于有限元法获取应力谱的高复杂度,安孟德等人考虑采用超声测量的方式采集螺栓应力,获取螺栓应力谱[14]。
本文针对2.0 MW 风力发电机组的高强度螺栓,基于超声波测量原理、S-N 疲劳寿命曲线、雨流计数法和Miner 疲劳累计损伤理论,系统地总结了一套螺栓疲劳损伤分析和预测方法。具体而言,本文通过安装超声探头和温度传感器的方式采集高强度螺栓应力数据,获取螺栓的载荷谱和应力谱;然后,采用四点雨流计数法将应力谱处理为三维的疲劳应力谱,提取应力循环数据,并基于Goodman 公式修正应力谱,获取修正后的应力循环次数、应力幅值;之后,基于螺栓S-N 曲线和Miner 线性累计损伤理论构建螺栓疲劳预测模型;最后,通过螺栓疲劳损伤估算和实验结果分析,验证所设计的疲劳损伤分析方法的准确性和可行性。
1 高强度螺栓疲劳预测算法
本文的研究对象为某2.0 MW 风力发电机组所使用的高强度螺栓,包括法兰盘连接螺栓和叶根螺栓。螺栓材料为42CrMoA 钢,性能等级为10.9 级,高强度螺栓型号包括M36、M42、M48、M56、M64。本文所设计的适用于风力发电机组高强度螺栓的疲劳预测流程如图1所示。
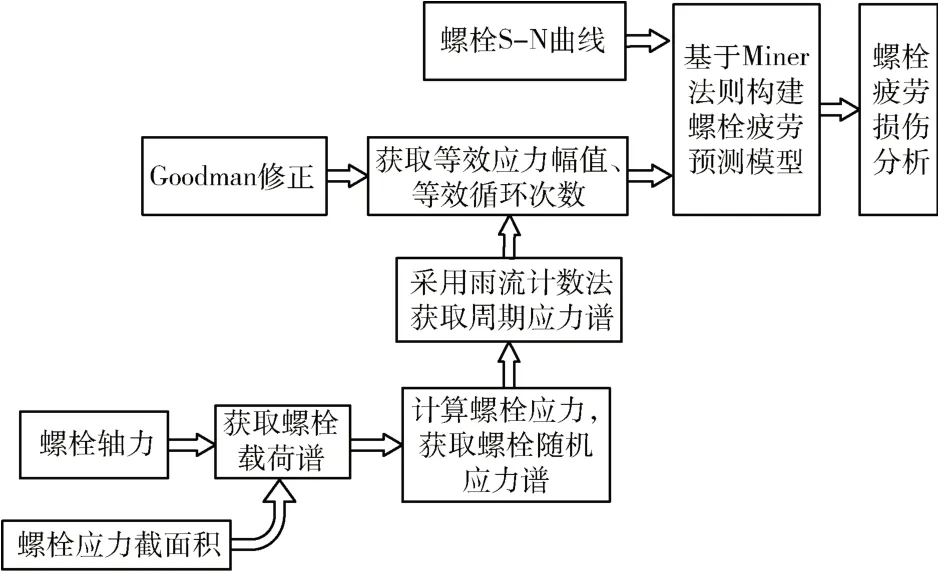
图1 螺栓疲劳预测流程示意图
本文所设计的适用于风力发电机组高强度螺栓疲劳预测的详细步骤如下:
(1)获取应力谱:通过超声探头采集螺栓数据,计算出螺栓轴力,并基于温度传感器进行温度补偿,获取螺栓载荷谱;再根据应力算法计算出螺栓应力,得到螺栓的时间-应力历程曲线,即螺栓应力谱;
(2)雨流计数法处理应力谱:首先,对应力谱进行预处理和数据压缩,剔除奇异值;然后,采用四点雨流计数法将其处理为三维的疲劳应力谱,并提取应力幅值、应力循环次数和应力循环平均值;
(3)Goodman 修正应力谱:采用Goodman 模型对处理后的应力谱进行修正,将实际工作循环应力转化为对称循环应力,获得等效应力幅值和对应循环次数;
(4)利用材料S-N 曲线,计算出螺栓各等效应力幅值对应的疲劳寿命;
(5)构建疲劳预测模型:基于Miner 线性累计损伤理论,构建螺栓疲劳预测模型,估算螺栓的累计疲劳损伤。
1.1 获取螺栓应力谱
螺栓应力谱是对螺栓进行疲劳预测和仿真实验的基础。本文采用在螺栓顶部安装超声探头和温度传感器的方式实时采集螺栓轴力,再根据螺栓应力计算公式,求出螺栓所受的轴向应力,则可获取螺栓的时间-应力历程曲线,即螺栓随机应力谱。
超声探头采集螺栓轴力的原理是基于超声纵波法和胡克定律,通过超声探头向工作状态下的测量螺栓发射超声纵波的方式采集超声纵波在测量螺栓中的传播声时,再通过测量螺栓非紧固状态下的超声纵波声时获取螺栓初始声时,即可计算出超声纵波在测量螺栓中的传播声时差。而且,考虑到超声波在介质中的传播声速受温度影响,本文还采用温度传感器采集螺栓实时温度,对采集到的声时差进行温度补偿。此外,采用符合GB/T 16825.1[15]的拉力试验机并根据GB/T 228.1[16]所规定的方法对螺栓进行拉力试验,采用超声探头采集螺栓回波声时并计算出声时差,得到轴力-声时差标定曲线,并采用最小二乘法拟合出螺栓的轴力系数。基于轴力标定系数和所采集的螺栓声时差即可计算出螺栓的轴向力,根据轴向力、应力截面积则可计算出螺栓的轴向应力。螺栓轴向应力的计算公式为:
式中,σi代表螺栓的轴向应力,单位为MPa;F代表螺栓的轴力,单位为kN;AS代表螺栓的应力截面积。螺栓的轴力可以通过对螺栓顶部安装轴力超声传感器进行轴力的采集。应力截面积AS计算公式为:
式中,d2为螺纹中径,d3=d1-;d1为螺纹小径,H为,P为螺距。
1.2 雨流计数法处理应力谱
应力幅值和循环次数是造成螺栓疲劳的主要因素,本节基于四点雨流计数法对前文所获得的螺栓随机应力谱进行处理,并提取出应力幅值、应力均值和对应的循环次数。基于四点雨流计数法的处理步骤如下:
(1)数据预处理:采用拉伊达准则剔除奇异值。首先求取测量值xi的平均值,并计算残差vi=xi-;然后求取标准差σ=螺纹原始三角高度且H=;对于数 据xi,若|vi|=|xi-| >3σ,则视为该数据为奇异值,进行剔除。
(2)数据压缩:剔除相邻等值或者呈递增/递减的无效数据点。若xi-1=xi,或xi-1
(3)提取峰谷值:对于非首端或末端的数据点,若(xi-xi-1)(xi-xi+1) <0,则认为数据xi为非峰谷值点,进行剔除。
(4)峰值拼接:提取整个应力谱数据的绝对值最大点,并对该点进行打断拼接,使得应力谱的首端和末端数据点为绝对最大值,从而保证雨流计数能够形成完整的循环。
(5)循环数提取:采用四点雨流计数法提取循环应力次数、应力幅值、应力均值。采用四点雨流计数法提取应力循环数据的算法伪代码如下:
1.3 Goodman 修正应力谱
螺栓疲劳预测需要在对称循环载荷(R=-1)下进行,然而实际螺栓工作在非对称循环条件下,因此需通过保守的 Goodman 模型将实际工作循环的应力水平等寿命地转化为对称循环下的应力水平。基于此,本文采用Goodman 模型对雨流计数法处理后的应力谱中的应力幅值、应力均值进行等效转化,获取等效应力幅值。Goodman 修正模型如下:
可转化为:
式中,Sa代表等效应力幅值;SR=-1代表对称循环下的疲劳应力幅值;Sm为平均应力值;Su为螺栓材料极限强度值。
1.4 螺栓S-N 曲线
材料的疲劳强度和疲劳寿命的关系通常采用应力-疲劳寿命曲线,即S-N 曲线来描述。S-N 曲线的幂函数形式的可表示为:
式中,Δσ代表螺栓所受到的平均载荷产生的应力,C和m分别代表螺栓的材料参数。为了更直观地观察S-N 曲线的特征,S-N 曲线通常表示为对数形式,其表达式为:
根据GL 规范[17],在双对数坐标系下,螺栓的S-N 曲线可以近似为两段相连的直线。其中,第一段斜率m取值为3,第二段m为5;拐点处应力幅值ΔσD对应的循环次 数ND取值为5 × 106;ΔσA为应力 循环次 数NA=2 ×106时对应的应力幅值。
对于直径超过M30 的螺栓而言,需要考虑螺栓直径缩减系数对S-N 曲线的影响,且螺栓的疲劳设计等级DC=71。根据S-N 曲线的表达式N·Δσm=C,可以得到应力幅值ΔσD与ΔσA的对应关系为:
根据GL 规 范[17]及Eurocode 标 准[18],ΔσA计算表 达式为:
式中,DC 代表螺栓的疲劳设计等级,取值为71;ks代表螺栓直径缩减系数;γM为螺栓疲劳安全系数,取值为1.15。螺栓直径缩减系数ks表达式为:
式中,ds代表螺栓的直径。
以M36 螺栓为例,可以计算出S-N 曲线拐点的应力幅值ΔσD=43.46 MPa。根据拐点的值即可计算出式(6)中的材料参数C。以M36 螺栓为例的S-N 曲线如图2所示。
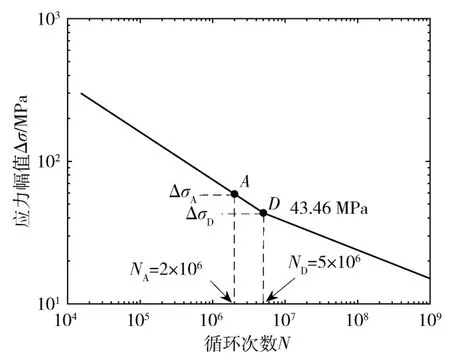
图2 螺栓的S-N 曲线
1.5 疲劳预测模型
一般情况下,S-N 曲线可直接用于恒幅载荷下的疲劳寿命预测。而对于变幅载荷谱,通常采用Miner 线性累计损伤理论进行疲劳寿命预测。然而,风力发电机组服役螺栓所受的载荷为随机载荷。对于这种随机载荷谱下的疲劳寿命预测,通常认为随机载荷谱等同于变幅载荷谱或恒幅载荷谱。本文根据Miner 线性累计损伤理论,将螺栓在随机载荷作用下的疲劳寿命视为轴向恒幅值应力作用积累的结果。根据Miner 线性累计损伤理论,可将各应力作用下所造成的螺栓疲劳损伤视为相互独立且可线性叠加的,则螺栓疲劳的判定准则可表示为:
式中,D为螺栓疲劳累计的总损伤,在设计寿命周期内应小于1;若总损伤D大于1,则判定该螺栓发生疲劳失效。ni代表各等效应力循环对应的循环次数,Ni代表SN 曲线中对应各等效应力循环的寿命。
2 实验结果与分析
本节针对某2.0 MW 风力发电机组的M36 型号的叶根螺栓进行实验,用以验证所设计方案的可行性。首先,在螺栓顶部安装超声探头以采集数据;然后,采用拉力机在其载荷范围内施加载荷;最后,基于所采集螺栓数据,根据前文所述的超声探头采集螺栓轴力原理和螺栓应力算法进行计算,即可获取螺栓载荷谱和螺栓疲劳应力谱。本文实验采集数据时长取10 min,所获得的螺栓随机载荷谱和螺栓随机应力谱如图3 和图4所示。
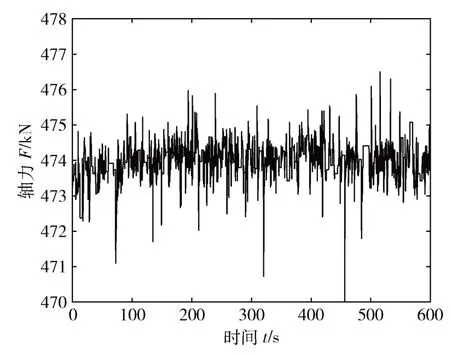
图3 螺栓的随机载荷谱
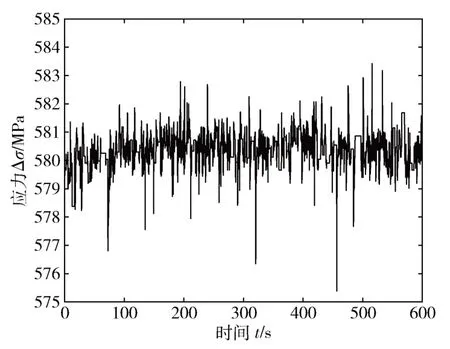
图4 螺栓的随机应力谱
螺栓疲劳应力谱在进行雨流计数法处理之前,需要经过数据预处理、压缩处理、提取峰谷值、峰值拼接的一系列处理来剔除应力谱中的奇异值,从而为雨流计数能够提取循环应力数据提供保障。根据前文所述方法,对随机应力谱奇异值数据进行剔除,可获得如图5 所示的周期应力谱。
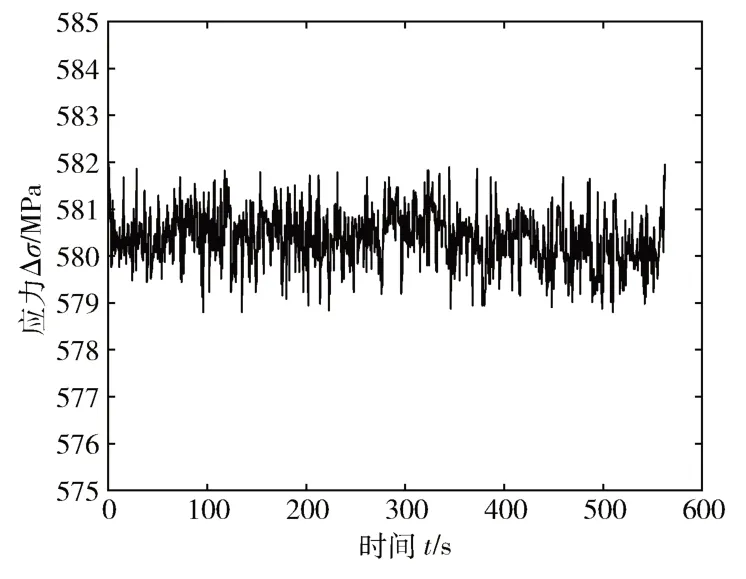
图5 螺栓的周期应力谱
采用四点雨流计数法处理剔除奇异值后的周期应力谱,则可获得螺栓疲劳应力谱的循环应力数据,包括各个子循环的应力幅值、应力均值和应力循环次数。根据算法1 所述的提取应力循环数据算法,可得如图6 所示的采用四点雨流计数处理后的疲劳应力谱。
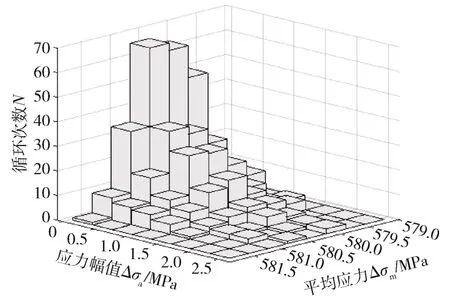
图6 雨流计数法处理后的疲劳应力谱
如图6 所示,采用雨流计数法所获取的疲劳应力谱是三维的,这些三维数据无法直接用于螺栓疲劳损伤的估算。本文采用如式(3)所示的Goodman 模型对所获取的三维应力谱数据进行修正和变换,并按照应力等级进行划分,可获得对称循环载荷下的等效应力幅值和等效应力循环次数。
根据前文的疲劳预测模型可知,由等效应力幅值和等效应力循环次数即可进行螺栓疲劳估算。首先,将等效应力幅值Δσ代入式(6)的S-N 曲线表达式中,可获得该循环应力下的疲劳寿命次数N;然后,将疲劳寿命次数N和等效应力循环次数n代入式(10)的Miner 理论表达式中,则可估算出该螺栓20 年的累计疲劳损伤为7.100 2 × 10-8,远小于螺栓疲劳极限,且疲劳寿命可达到1.408 4 × 107的循环次数。因此,可预测本文实验所采用的螺栓在20 年疲劳载荷作用下不会发生疲劳失效,满足风力发电机组高强度螺栓的寿命要求。
3 结论
本文针对2.0 MW 风力发电机组高强度连接螺栓的疲劳损伤问题,基于超声测量原理、螺栓材料S-N 曲线、雨流计数法、Goodman 修正公式、Miner 累计损伤理论,系统地总结了一套螺栓疲劳损伤分析和预测方法,该方法能够为风电行业连接螺栓疲劳分析提供可靠的理论依据,具有较高的工程应用价值。研究结果表明,所估算的螺栓螺栓疲劳损伤为7.100 2 × 10-8,明显小于疲劳极限,能够满足风力发电机组20 年的设计寿命要求。
