金属封装微系统内部高压击穿和爬电问题的点云分析方法*

王 辂，柏晗，曾燕萍，丁涛杰

（中国电子科技集团公司第五十八研究所，江苏 无锡 214000）

0 引言

微系统技术将多个半导体芯片整合到一个封装中，并通过各种封装技术将它们电气互连，以创建接近片上系统的系统，但具有更好的良率、更高的灵活性和更快的上市时间[1]。将高压隔离芯片、控制器、配置电路等模块集成为微系统形态能够明显缩小产品尺寸、提升场景适应性。然而，在有限空间下，产品封装后将引入键合线、管壳、盖板、焊柱等其他金属结构，是否会因此产生新的击穿行为行业内尚无方法能够分析确定，却是这类微系统器件在设计时必须予以考虑的可靠性因素。

分析多款产品的物理构成后发现，隔离微系统内部的击穿问题可归纳为两类：基板表面隔离前后两网络的最小间隔小于隔离强度从而发生的表面爬电现象，以及空间中隔离前后两网络因封装金属结构导致的空间击穿现象。本文基于空间几何思想对上述物理现象进行转化：将空间击穿问题等效为求解空间中两点间的直线距离，即欧氏距离；将表面爬电问题等效为求解空间中两点在表面上的最短连接距离，即测地距离。通过分析两种路径的位置及长度，判断产品封装后的电学可靠性。

使用点云模型描述物理结构是将现实物理世界转化为可计算结构的重要手段[2-3]，三维点云数据可利用算法拟合或建模软件生成，具有精度高、细节完整、建模速度快等优势。数据中带有空间坐标，有利于描述空间几何关系，广泛应用于测绘、自动驾驶、规划设计、电力、建筑、工业、考古、医疗、游戏、刑侦等众多领域[4-6]。将三维物体转化为点云模型有正向和逆向两种方法[7]，前者可将三维几何模型直接转化为点云模型，从而在设计初期对产品进行预先分析；后者可利用激光雷达、深度相机等设备获取产品的外观表面及点云数据，用于对已有产品的逆向分析[8]。实际建模时需根据目标的当前状态选择合适的方法。

针对隔离微系统中的击穿问题，本文将其物理结构转化为点云模型，并依据等效规则进行点云计算，实现对微系统内部潜在击穿风险的判断和分析。为验证总体路径的有效性，本文将同时采用正向和逆向两种手段进行建模。

1 微系统的点云建模及分析方法

1.1 微系统的点云建模

将微系统模型转化为点云模型前，首先应明确分析问题的类型：对于表面爬电行为，需考虑基板及焊盘、键合指等基板表面的金属互联结构；对于空间击穿行为，则需要进一步考虑金属外壳在内的一体化模型。

采用正向方法构建点云模型时，主要包括以下步骤：首先建立精确的微系统三维几何模型，需包含如裸芯、阻容、键合线、焊盘、引脚等全部精细结构；再依次转化为*.stl 和*.obj 网格文件；之后，利用采样程序，按行、列形式扫描三维模型，最终得到包含点云数据的*.pcd微系统模型。

采用逆向方法构建点云模型时，主要通过深度相机对微系统进行高精度扫描，之后将数据转换为点云格式，再进行计算处理。这种方法充分还原了工艺过程中的随机性，可完整展现产品的真实物理形态。

1.2 微系统内部击穿和爬电问题的点云分析方法

1.2.1 最短路径寻找方法

点云模型中，从某顶点沿图的边到达另一顶点所经过的路径中，各边权值之和最小的一条路径叫做最短路径，是图论研究中的一个经典问题。典型方法有Dijkstra 算 法[9]、Floyd 算 法[10]、Bellman-Ford 算 法[11]和SPFA算法[12]等。其中，Dijkstra 算法采用广度优先搜索策略，以起始点为中心向外拓展，依次计算出单点到图中所有点的最短距离，直至扩展到终点为止，从而得到全局最短路径树，是寻找指定两点间的最短路径时一种有效手段。对于如图1 所示的模型中，计算A-F之间的最短路径，可归纳为以下步骤：

(1)将起点A放入集合中，A点的权值为0，因为A->A=0；

(2)与起点A相连的所有点的权值设置为A->点的距离，连接不到的设置为无穷，找出其中最小权值的B放入集合中(此时A->B必定为最小距离)；

(3)将与B点相连的所有点的权值设置为B->点的距离，并且找出其中最小权值的C点放入集合中(此时C的权值必定为其最小距离)；

(4)重复步骤(3)，直至所有点加入集合，即可得到所有点与A点的最短距离。

上述流程可在微系统模型中寻找出目标位置所有可能的路径，保证计算结果的全面和准确，并可根据模型实际情况优化算法结构以提升计算效率。

1.2.2 击穿和爬电路径计算流程

本文利用PCL 库对点云数据进行处理，主要涉及点云获取、滤波、分割、配准、检索、特征提取、识别、追踪、曲面重建和可视化等操作。并针对微系统的物理形态，开发基于Dijkstra 算法的最短路径计算方法，模拟微系统内部的击穿和爬电现象，主要流程如图2 所示。

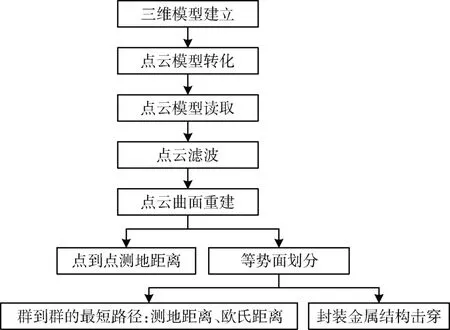
图2 击穿和爬电路径点云计算流程

(1)三维模型建立。建立详尽的、精确的微系统三维模型，对于设计中产品，可根据实际工艺参数和布局情况建模，属正向手段；对于已有产品，还可利用深度相机等设备进行扫描，完整还原当前产品的实际三维结构。

(2)点云模型转化。将三维模型转化为点云模型，采样可使用均匀采样和随机采样，前者更适用于形态规则的产品，后者对模型无要求，适应性更为广泛。包括正向方法和逆向方法，均可形成完备的点云模型，之后即可传递至计算模块进行处理和分析。

(3)点云模型读取。为便于后续的分区处理、模块识别以及图形显示，需先对pcl::PointXYZ 类型的点云进行着色。读取点云中每一个点的XYZ 坐标，并为其附上RGB 属性，从而将其转换为带有RGB 颜色属性的pcl::PointXYZRGB 类型的点云。

(4)点云滤波。为更好地执行配准、特征提取、曲面重建等操作，需首先进行点云滤波。特别对于点云数据密度不规则、模型中存在离群点(即噪声点)、数据规模量过大等情况，滤波是必要操作。本文采用VoxelGrid滤波器对点云进行下采样，在保持原数据特征的基础上平滑点云数据、滤除离群点、降低点云规模，从而提高曲面重建效率和路径计算效率。

(5)点云曲面重建。滤波后的点云仍是离散数据，无法表示物理模型的外观表面。此时，若直接进行最短路径计算，将出现两点“穿过”物体内部的现象，不符合真实情况。因此，需要对点云模型进行曲面重建。本文采用贪婪投影算法对点云进行快速三角化，先用pcl::NormalEstimation 类中的compute 函数计算所有点的法线，从而将无序点云转换为有向点云，再使用pcl::GreedyProjection Triangulation 类中的reconstruct 函 数，对有向点云进行重建，同时禁止平滑处理和孔洞修复，在不改变原有数据的前提下重构几何表面，从而明确爬电路径所在面以及表面各点之间的连接关系，保证了后续计算的真实性。

(6)点到点的测地距离计算。根据以上步骤得到的各点坐标、各点链接关系以及重建的曲面，“点到点的测地距离”就可以转化为图论研究中无向图最短距离计算的问题。本文根据微系统中的实际需求，改造Dijkstra算法：首先，将std::vector 类向量容器转换为各点及其所有邻接点的连接关系，以此作为Dijkstra 算法的输入参数；之后，定义一个等长的向量容器，用于存储与上一点最邻近点的序号；当所有点的最短距离遍历完成后，即可根据容器中的序号确定最短路径的位置以及该路径的距离值。

(7)等势面划分。在内部存在压差的微系统中，导电材料(焊盘、键合线、铜片)具有各自的电势。在计算测地距离之前，首先需要确定起点和终点分别所在的导电材料位置。为此，本文设计了一种描点划线算法，依据两等势面之间的折线计算出每段折线的线性方程，再将点云中导电材料的点坐标代入方程求解，从而划分出各个等势面。并将每个等势面定义为一个“群”，以区分各部分电势。

(8)群到群的最短路径计算，包括群之间的欧氏路径和测地路径，用以确定隔离前后两个网络间的最短路径，进而判断击穿与爬电的可靠性风险。理论上，只需要对两群中每个点进行一次最短路径计算，再筛选最小值即可确定群之间的测地距离，然而该方法的执行效率极低。因此，本文对此进行优化：首先，根据等势面标记起始群和结束群进行标记；之后，从起始群的某一点开始寻找最近邻接点，判断该点是否属于结束点群，如果不是，则寻找下一个邻接点，如果是，则标记该点为起始点的最短路径终点，退出Dijkstra 算法；循环上一步，直至找到所有最短路径终点，其中的最短路径即为两群的最短路径。

Dijkstra 算法的广度优先搜索原则保证该优化算法的有效性，即每找到一个最近邻接点，可确保不会再出现第三个点满足更短路径的情况。而剩余未找到的点，到起始点的最短路径一定大于当前路径。因此，只要确定找到的最近邻接点是属于结束点群的，则可以直接退出Dijkstra 算法。

(9)封装金属结构击穿。在引入键合线、管壳等结构后，若微系统内部连接与等势面距离过近无法满足电气间隔，将发生击穿。本本采用隔离两侧点群到盖板等结构的欧式距离进行表示，例如，键合线中的在垂直方向上的最高点坐标与盖板在垂直方向上的坐标差即为二者的最短距离。因此，该问题可以等效为寻找一组点群内在某个方向上的极值点的坐标。

2 微系统击穿与爬电的点云计算案例

2.1 基板表面爬电路径模拟

为验证该方法的有效性，根据某型微系统结构建立验证模型：在玻璃表面粘贴平行铜带，即满足理想等势，在尺度上又与真实接近，同时可模拟工艺过程中的误差和随机性，验证算法的精确程度。之后依照上述流程进行建模仿真，结果如图3 所示。

图3 基板表面爬电路径模拟

很明显，仿真与实测表现出的击穿位置是完全一致的。尽管两个等势面间的边界是“平行”的，但由于过程的随机性，存在尖端突起或非均匀位置，从而发生爬电现象。

仿真结果为，基板模拟结构一的最短距离为153.184，结构二的最短距离为217.264。值得注意的是，上述仿真结果中，距离值依赖点云模型大小，是几何模型中的相对距离，其单位为像素点(px)，并非真实实验距离，转化后得到结果如表1 所示。

表1 点云仿真结果长度转化

为明确在玻璃砖表面爬电距离与爬电电压的关系，设置等间距铜带击穿试验，并进行多次击穿，获取击穿电压，去除最高最低求平均，得到如表2 所示结果。

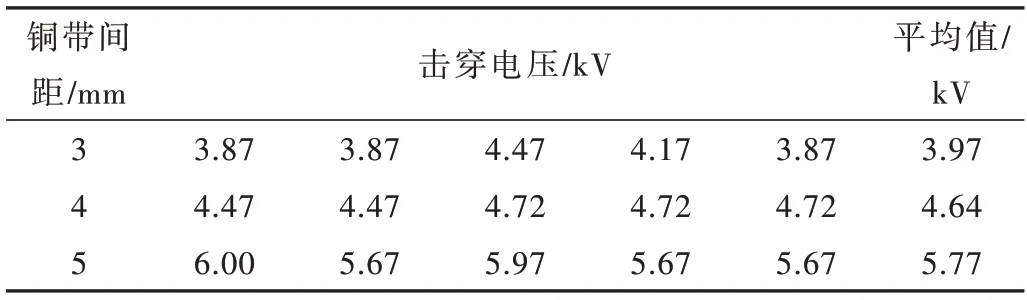
表2 玻璃砖表面爬电间距与电压测试结果

可以看出，在同一玻璃砖表面，击穿电压与距离基本成线性关系。将表1 中的结果进行等比计算，并与实际击穿电压进行对比，得到如表3 结果。

表3 玻璃砖表面爬电电压测试与计算结果

可以看出，计算结果与测试结果存在少量误差，趋势匹配良好，主要原因在于曲面重建时采用了三角面片的结构，路径计算时必须沿着三角面片的边行进，故算出的路径存在曲折前进的现象，由此引入的总体误差在可接受的范围内。该问题中的模型转化流程为二维图像→图像识别→三维建模，在一定程度上存在与原模型的偏差，若使用更精确的模型，可进一步缩小误差。该验证模型有力证明了所提出方法的有效性。

2.2 微系统基板表面爬电路径

下面以某型微系统产品为例进行分析。采用正向方法建立微系统基板的正面和背面模型如图4(a)和图4(c)所示。建模时，将基板表面金属层及焊盘底部挖空，形成“壳体”模型，这样既不影响路径计算，也可以增加目标区域的点密度，同时避免“结构内部击穿”的不合理现象。参照上述流程计算隔离两侧间的最短路径，即为潜在的爬电路径，如图4(b)和图4(d)所示。再依据上例中的流程，确定该基板材料表面爬电距离与隔离电压之间的关系后，即可判断基板表面是否存在爬电风险。

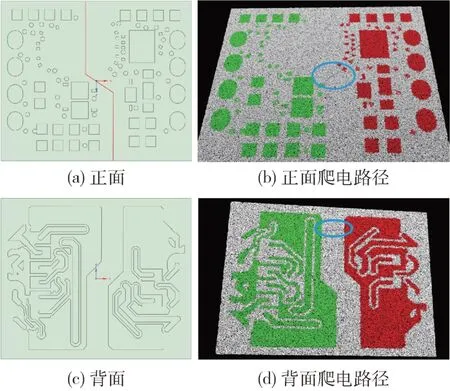
图4 微系统基板的三维模型

2.3 互联结构与金属壳体的击穿行为

以同型微系统为例分析其互联结构与金属壳体间的击穿风险。建立基板、键合线以及与之相连的芯片、焊盘、引脚等结构，如图5 所示，并用空间坐标值等效金属壳体以提高计算效率。进一步计算这两个距离和，即可判断是否存在壳体电击穿风险。

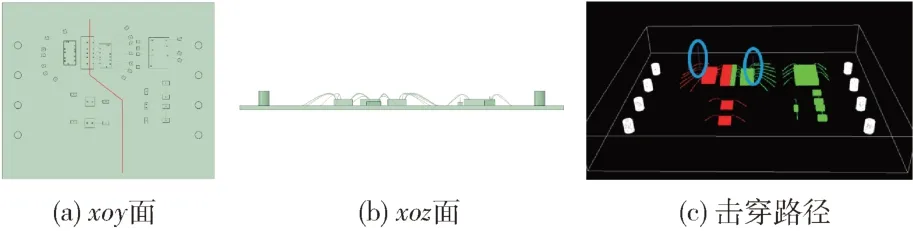
图5 微系统三维模型

图中黑线即为隔离前后端的分界线。到封装壳的距离包括焊柱到边缘的距离、键合线到顶部的距离，外壳在x和y方向上的边界为基板的边界；在z轴方向上，以基板上表面为基准，上方2.5 mm 为外壳。该模型中，键合线高度在合理的范围内浮动，以模拟工艺随机性。产品中，金属壳体与坐标轴平行，因此可用垂直壳体的坐标轴位置模拟壳体，而无需真实建立，以提高计算效率。计算结果如图5 所示，两垂直线长之和即为判断是否满足电气间隔的依据。

3 结论

本文利用点云分析手段、优化Dijkstra 算法实现对微系统内部潜在的击穿和爬电风险的分析，为行业的痛点问题提出新的解决思路。对照实验表明，仿真与实测结果间的误差为8%～12%，充分表明这种分析方法的有效性。此外，可以看出，现有处理方式是比较理想的，在真实问题中，除了各个部件的大小和位置，还要考虑键合线的高度、管壳的位置和形状、绝缘材料的异型结构等，对仿真工作带来了巨大的挑战。因此，后续将在此基础上，围绕测地距离、物理建模、算法加速、验证实验等方面继续研究，提高对复杂问题的分析能力，拓展软件实用价值。