基于像素标记法的复合材料异型构件均匀性表征

张玉燕, 李启航, 温银堂

(1. 燕山大学 电气工程学院，河北 秦皇岛 066004；2. 燕山大学 测试计量技术及仪器河北重点实验室，河北 秦皇岛 066004)

1 引 言

纤维增强陶瓷基复合材料是一种集结构承载和耐苛刻环境的轻质新型复合材料,由于具有高比模量、高比强度、低热膨胀系数、耐高温、耐腐蚀等许多优良特性,已被广泛应用于航空航天领域[1,2]。因其制作工艺多样,制作步骤复杂,在材料制备过程中,内部容易产生分层、裂纹、孔隙和密度不均等缺陷。这些制造缺陷导致结构不均匀,对纤维增强复合材料的宏观力学性能包括强度、有效弹性模量等有很大影响[3]。因此,定量表征出纤维增强型陶瓷基复合材料的均匀性,对优化制备工艺参数、增加构件寿命、提高服役可靠性等都具有非常重要的意义。

目前关于复合材料的均匀性表征研究,大多数围绕颗粒增强相在复合材料中的分散均匀性展开。Zhang L等就微观尺度评价复合材料增强相颗粒分散均匀性的方法进行了综述[4]。然而,围绕制造缺陷对复合材料进行均匀性表征的研究较少。孔隙作为陶瓷基复合材料无法避免的一种制造缺陷[5],其分布的不均匀会导致构件服役时在孔隙富集区产生较大的应力集中,极大地降低构件可靠性[6～9]。因此,围绕孔隙缺陷展开对复合材料的均匀性定量表征研究很有必要。目前已有一些学者进行了相关研究,付云伟等根据陶瓷材料的断面显微照片,从二维层面对孔隙富集的局部区域进行模型等效分析,结果表明孔隙分布均匀度对材料强度有很大影响[10]。陆铭慧等基于超声声速、声衰减,间接对陶瓷基复合材料矩体样件的密度和孔隙均匀性进行了量化表征,指出样件的密度不均匀是由孔隙不均匀引起的[11]。

但是超声检测对于不规则样件存在一定的局限性[12,13]。多数研究的试样均为规则样件,而航空航天领域复合材料制件往往结构形式复杂,且制件结构的复杂性直接影响制造缺陷的出现比例[14,15],也就使得因制造缺陷引起的材料不均匀问题更加突出。对复合材料内部的孔隙缺陷检测,工业CT是一种有效的无损检测手段[16,17]。通过CT扫描获得样件内部缺陷的图像灰度信息,利用图像处理方法能够计算出构件整体的平均孔隙率[18],但由于无法反映局部孔隙缺陷的聚集程度,不足以有效表征构件的结构均匀性。

针对上述问题,本文以连续纤维增强的陶瓷基复合材料异型构件为研究对象,基于CT扫描的断层图像序列,提出了一种空间区块划分的方法,完成了对异型构件局部和整体的均匀性定量表征,并利用三维重建方法对缺陷特征量进行三维映射,对表征结果进行直观的三维成像。

2 基于像素标记的均匀性表征原理

2.1 自适应双阈值OTSU算法

本文构件由密度较低的碳纤维增强体、密度较大的基体碳化硅以及内部缺陷三类组成,密度的不同体现为断层图片上灰度值的不同,针对此特点,本文选择双阈值OTSU算法进行孔隙分割。假设断层图像的灰度级为L,阈值T1,T2将图像分为3类:G0=(0,1,…,T1),G1=(T1+1,T1+2,…,T2),G2=(T2+1,T2+2,…,L)。假设灰度值为i的出现概率fi,图像整体的灰度均值为μ,Fk为每个类的出现的概率,k=(0,1,2)。

(1)

每类的灰度均值为:

(2)

类间方差为:

(3)

使得类间方差最大的阈值集合就是双阈值OTSU的最佳阈值集合:

(4)

图像中孔隙属于灰度均值最低的类,故以T1作为全局阈值对孔隙进行二值化分割。考虑到受样件形状和射线束硬化伪影的影响,断层图像亮度不均,单一的全局阈值难以取得较好分割效果的问题,本文使用了一种滑动窗口与双阈值OTSU结合的自适应阈值分割算法,其流程如图1所示。

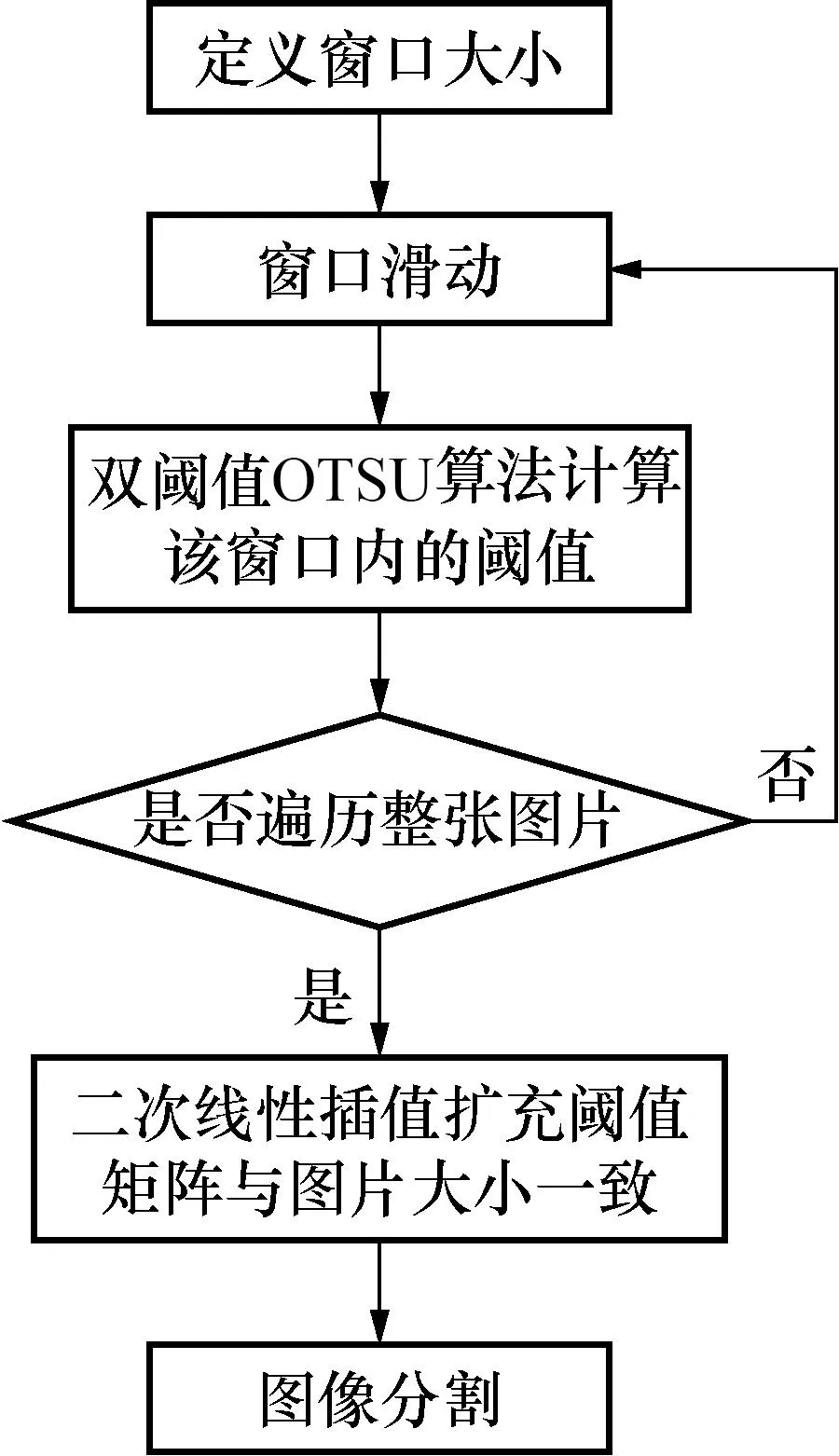
图1 自适应双阈值OTSU算法流程Fig.1 Adaptive double threshold OTSU algorithm process

2.2 区块划分

由于整体的平均孔隙率无法有效表征构件的结构均匀性,所以对样件进行区块划分,通过局部孔隙率的差异来反映均匀性。

三维体数据由若干二维断层图像重构而成,要实现三维上对构件的区块划分,就要对二维断层图像上不同区块进行标记,隶属同一区块的像素点有相同的标签值,标签值的计算公式如下:

(5)

式中:x为目标像素在分块方向上的坐标值,x∈[a,b];k为断层图像的序列值;n、m分别为二维图像上的分块个数和断层序列上的分块个数;step1为断层图像上分块的步长,以像素为单位;step2为断层序列上分块的步长,以图像的张数为单位;N为断层图像序列的总张数;ceil表示向上取整。区块划分的示意图如图2所示。

图2 区块划分示意图Fig.2 Diagram of the division of blocks

2.3 均匀性定量表征

2.3.1 分区孔隙率计算

假设材料的三维体数据是由N张CT断层图像构成,若CT扫描的分辨率为p,则重构的体数据中每个体素尺寸大小为p×p×p,经过分割和标记,可以统计出第k幅断层图像中标签值为i,且属于孔隙的体素个数为Nhki,属于材料部分的体素个数为Nmki,则标签值为i的子块中,材料总体素个数(同时包含材料与孔隙部分)为:

(6)

孔隙部分体素个数为:

(7)

体孔隙率为:

(8)

2.3.2 均匀性定量指标的建立

样件某个区域内的孔隙率越低,孔隙的分布越均匀,认为样件的结构均匀性越好。即一个区域内孔隙率的均值越低越好,孔隙率的标准差越低越好。据此,提出将孔隙率的均值与标准差的乘积作为孔隙分布均匀性的衡量指标。均匀性指标H越小,均匀性越好,反之越差。

H=μσ

(9)

式中:μ为区块孔隙率均值;σ为孔隙率标准差。

2.4 体孔隙率的三维映射

2.4.1 孔隙率归一化

为了将材料不同位置上的孔隙率值映射为图像信息(即灰度值),需要对孔隙率进行归一化。由式(8)可以得到所有区块中孔隙率最大值Pmax和最小值Pmin,根据归一化公式将不同区块的孔隙率值归一到指定灰度级区间[p,q]上:

Y=m+k(X-Pmin)

(10)

(11)

式中:k为归一化系数;X为孔隙率;Y为归一化值。

本文采用体绘制中的光线投射算法对包含孔隙率信息的二维图像序列进行三维重建[19,20]。

基本步骤是先将得到的数据根据灰度值进行分类,定义传输函数赋予每一个数据点颜色值和透明度值;接着沿与成像平面垂直的路径,按照预先设定的采样步长进行重采样,由三线性插值得到重采样点的颜色值和不透明度;最后依据合成规则对路径上的采样点进行合成,得到三维重建后的图像。

光线投射法在图像中的合成,采用由前向后的合成方式,合成递归方程为:

(12)

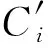
(13)

式中:C为最终的合成颜色;Ci与αi分别为采样点i沿入射光线的颜色值和不透明度。

3 实验与结果分析

3.1 样件与实验条件介绍

3.1.1 样件介绍

本文所使用试样为西北工业大学利用化学气相渗透法制备的碳纤维增强陶瓷复合材料构件,沉积温度约为1 000 ℃左右,基体为碳化硅,增强体为碳纤维编织成的二维叠层碳布,样件外形为“U”型,厚度为2.5 mm,实物如图3所示。

图3 构件俯视图及侧视图Fig.3 Top and side views of the components

3.1.2 CT扫描实验参数

这房子在旷野里，才会这么冷，青梅居的九楼，也有从旷野里吹来的风雪，青梅居会冷吗？应该不会的吧，那新建的房子，不是吹嘘有外墙保温系统吗？即使没有，新建的楼房，密封也好，怎么会任由这北风呼呼地吹进来又呼呼地吹出去？李倩倩、弟弟和妈，此刻都睡在那栋房子里，他们都不会感觉到寒冷。

本研究采用nanoVoxel-4000型开管反射式高穿透CT系统进行X射线断层扫描实验,其最高分辨率可达0.5 μm。该系统由X射线源、高精度转台、和平板探测器组成如图4所示,实验扫描参数如表1所示。

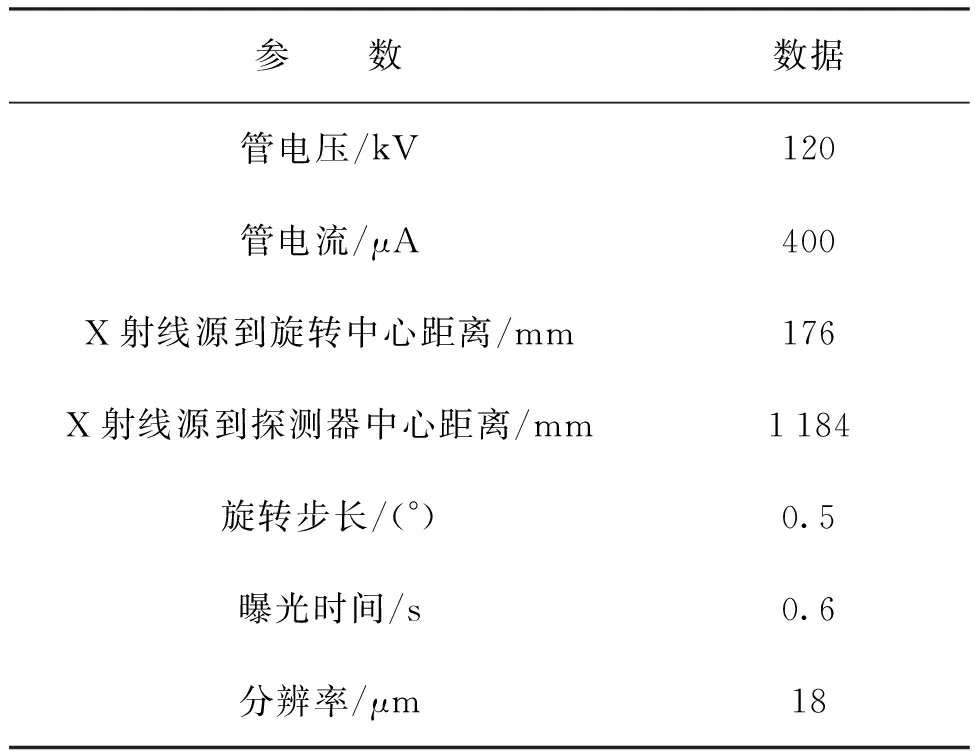
表1 锥束扫描参数Tab.1 Cone beam scanning parameters

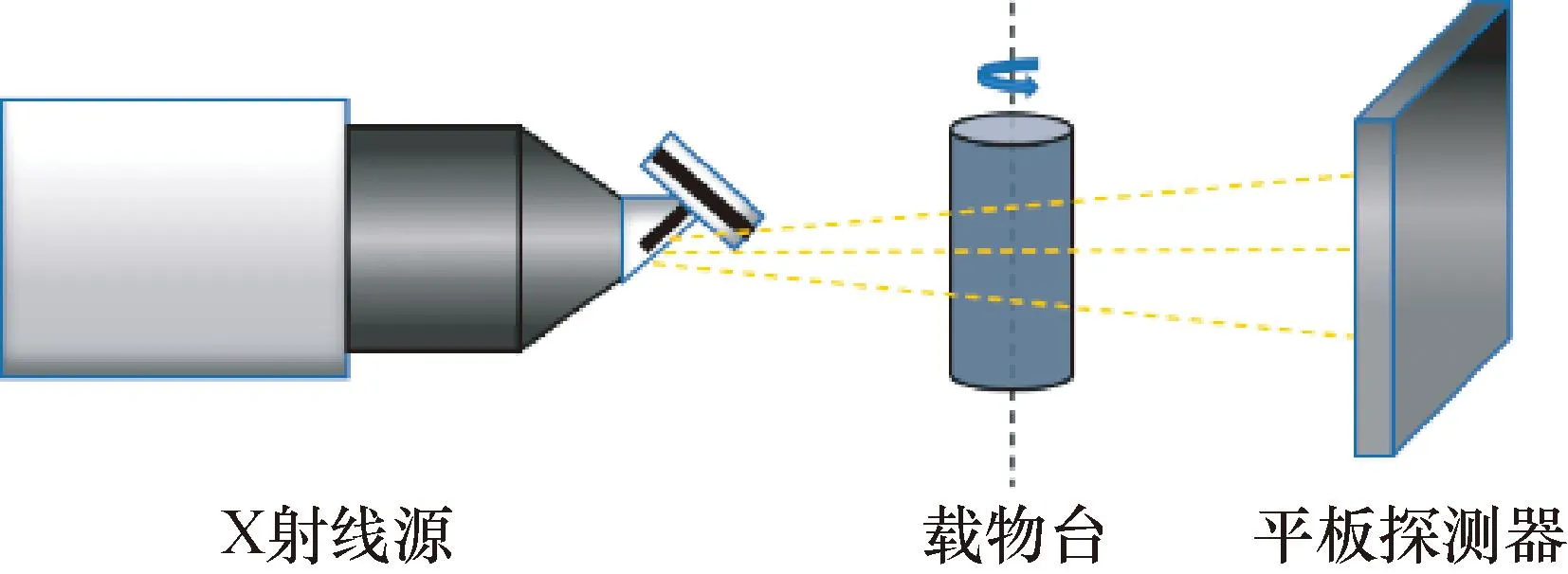
图4 CT系统的组成Fig.4 Composition of the CT system

受样件长度影响,对3个局部位置进行了断层扫描实验,分别记作1#、2#、3#(如图3),每段长度约32 mm。每个位置断层序列图像为1 795张,每张图像的尺寸为1 625×1 746像素,断层图像序列之间的间距为一个像素大小,即0.018 mm。

3.2 孔隙分割结果

断层图像在样件弯曲部位较其他位置存在明显的灰度值偏低现象。故本节以弯曲位置为例,比较了两种算法的分割效果。双阈值分割存在一定程度的欠分割现象如图5(b),自适应的双阈值OTSU算法,欠分割现象有了明显改善,如图5(c)。

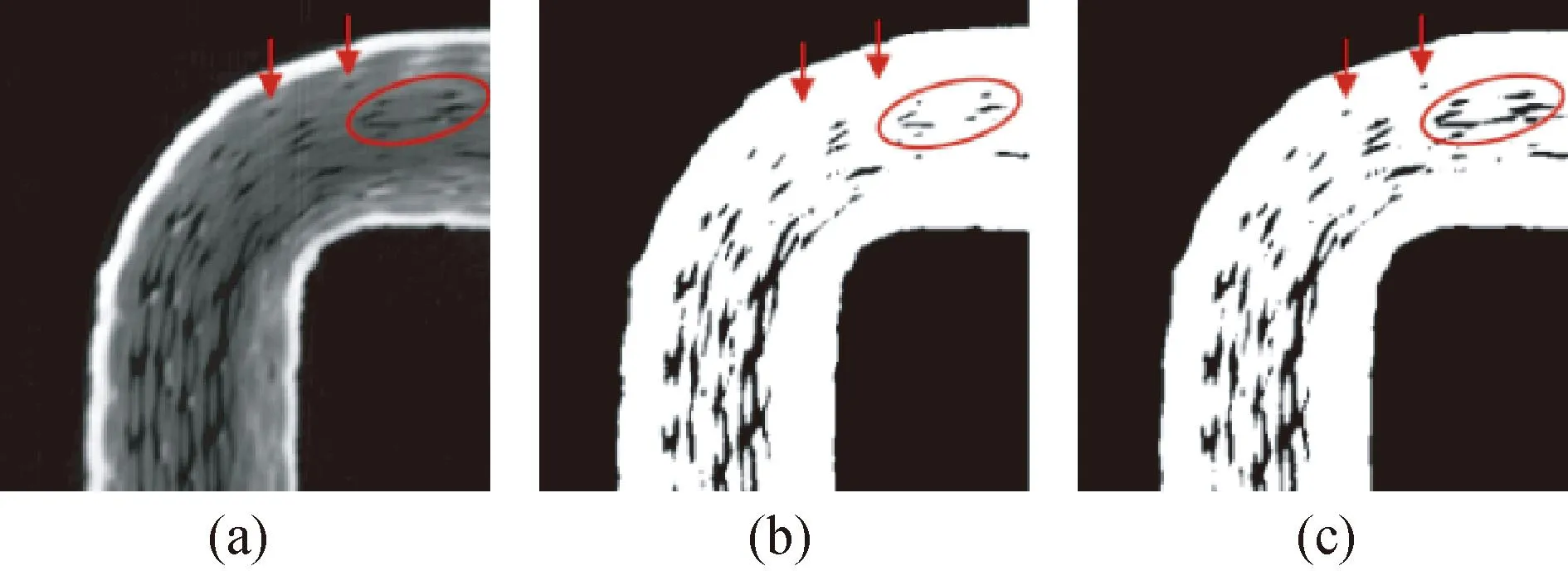
图5 孔隙分割结果对比Fig.5 Comparison of Pore Segmentation Results

由于背景与孔隙的灰度值接近,图像进行二值化时,背景与孔隙均被赋值为0。为了便于计算体孔隙率值,需要单独提取出孔隙和前景掩膜。首先对前景掩膜进行提取,基于自适应阈值得到的二值图像如图6(a),使用形态学闭运算,关闭内部孔隙得到前景掩膜如图6(b)。图6(a)与图6(b)进行异或运算完成对孔洞的提取如图6(c)。

图6 样件掩膜及孔隙提取Fig.6 Sample masking and pore extraction

3.3 区块体孔隙率统计分析

针对本文的“U”型样件,首先将样件分为①～⑤共5个区域,如第2.2节中图2,单独对每个区域进行区块划分,并依据式(8)计算不同区域每个区块的体孔隙率,区域划分的示意图如图7所示。

图7 区域划分及滑动窗口示意图Fig.7 Diagram of the zoning and sliding window

本文对1#、2#、3#进行了数量为60、90、138的区块划分并计算了体孔隙率,基于均匀性指标H对3个位置上的孔隙率进行统计分析,如表2、表3所示。

表2 138个区块的孔隙率统计分析Tab.2 Statistical analysis of porosity for 138 blocks

表3 不同区块数量下的孔隙率统计分析Tab.3 Statistical analysis of porosity at different block counts

由表2知,3个位置局部区域的孔隙分布均匀性为:区域①里3#<2#<1#,区域②里1#<3#<2#,区域③里3#<2#<1#,区域④里3#<2#<1#,区域⑤里2#<1#<3#。

由表3可知,在区块划分数量不同时,对于1#、2#、3#的均匀性判断结果一致均为2#<3#<1#,即,1#的整体均匀性最好,3#次之,2#最差。

3.4 绘制孔隙率三维云图

本文断层图像的位深为8位,灰度级范围为 0～255。将孔隙率映射为灰度值时,为必避免三维重建时与背景(灰度值为0)混淆,将所有区块的体孔隙率归一化到区间[1, 255]。整个映射过程如图8所示,图8(a)为原始图像,经过大津阈值与形态学闭运算得到样件掩膜图8(b),经区块划分得到图8(c),最后将归一化将每个区块上的体孔隙率值映射为灰度值,得到包含一系列包含孔隙率信息的灰度图像序列如图8(d)。

图8 分块孔隙率映射过程Fig.8 Fractal porosity mapping process for tomographic images

如图9对孔隙缺陷及孔隙率分布云图(区块数量为138)进行了三维重建,孔隙率三维云图与孔隙缺陷实际分布的疏密程度基本一致,区块孔隙率的最大值为15.895%,最小值为0.099%。通过颜色变化,可以对样件不同部位的均匀性做出一个较为可靠的定性判断。3个样件孔隙率在区域④两侧存在明显的梯度变化均匀性较差,而在区域②里3个样件均表现出较好的均匀性。

图9 样件孔隙缺陷及孔隙率三维分布云图Fig.9 3D distribution of sample porosity defects and porosity

4 结 论

本文针对复合材料异型构件整体孔隙率无法有效表征因局部孔隙聚集导致的结构不均匀,提出了一种基于像素标记的区块划分方法,实现异型构件各个区块体孔隙率的计算,以局部孔隙率均值与标准差之积为指标,对样件整体和局部的均匀性进行了定量表征。并利用光线投射算法对样件局部孔隙率分布进行三维可视化。结果表明:均匀性指标H的定量表征结果与可视化的定性表征结果吻合,本文方法能从宏观上准确直观的定量表征出异型构件的结构均匀性,为进一步探究孔隙三维分布均匀性对复合材料异型构件性能的影响打下了一定的基础。