分离式霍普金森压杆试验中金属材料端面摩擦效应误差分析

张柱柱,毛海涛,周圣林,焦 鹏,胡文林,吴省均,刘 军,张 旸,沈 沛,刘宇麟

(92728部队,上海 200443)

0 引 言

在分离式霍普金森压杆(split Hopkinson pressure bar, SHPB)试验中,试样与杆件端面的摩擦限制了试样在高速冲击作用下的侧向变形,即受到侧向惯性约束的影响[1-2],导致轴向抗压强度提高,从而使应力-应变曲线出现误差[3]。影响端面摩擦效应的主要因素包括端面摩擦因数、材料、试样长径比、试样形状和端面不平行度等[4-7],目前已有国内外学者通过试验和数值模拟法对端面摩擦效应的影响因素进行了研究。LU等[8]对硅橡胶、聚酯氨酯泡沫、奥克托金基聚合物黏结炸药和铝合金4种材料在润滑、干摩擦和黏接3种摩擦条件下的端面摩擦效应进行了试验研究,发现不同材料的端面摩擦效应机理不同,并且材料泊松比、端面摩擦因数、试样长径比和轴向应变是影响端面摩擦效应的主要因素。李晓琴等[9]通过试验方法研究了端面摩擦效应对混凝土材料动态增加因子(DIF)的影响,发现难以通过试验方法测得端面摩擦因数,只能做定性分析,而数值模拟方法可以对摩擦效应进行定量分析。LI等[10]通过数值模拟方法对材料动态强度变化进行了研究,认为SHPB试验中的侧向约束是导致动态抗压强度提高的原因。PING等[11]从端面摩擦因数、试样不平行度和试样直径3个方面研究了端面摩擦效应,并对端面摩擦效应进行了敏感性分析,确认灵敏度序列为端面摩擦因数、试样不平行度和试样直径。ZHONG等[12]分析了单层和多层结构圆柱和立方体试样的应力状态,认为界面摩擦对SHPB试样的应力三轴度和Lode参数有很大影响。TAKESHI等[13]在能量守恒的基础上探讨了SHPB技术的基本原理,并对径向动量守恒进行了一些修正,指出SHPB试样的径向惯性效应和端部摩擦效应相互耦合。ALVES等[14]分析了圆环在轴向压缩下的变形行为,认为圆环形状相比传统圆柱体形状更有利于消除试样端面摩擦效应的影响。王晓燕等[15]运用能量守恒法对端面摩擦效应机理进行探讨,推导出了端面摩擦效应理论分析公式。陶俊林等[16]在对SHPB惯性效应分析的基础上,增加了端面摩擦做功对试样惯性效应的影响分析,并对SHPB试样尺寸比例的设计及摩擦因数的选取进行了推导。HAO等[17]讨论了长径比和摩擦因数对不同应变速率下中尺度混凝土试样应力应变分布和破坏过程的影响,提出了消除端面摩擦约束对SHPB试验中混凝土材料动力强度增量影响的经验公式。俞晓强等[18]将Johnson-Cook本构方程的硬化项乘以1.2获得修正系数,对SHPB试验结果进行了修正。

综上可知,端面摩擦效应对SHPB试验结果存在重要影响,但其影响规律、具体量值、如何降低其影响等方面尚需进一步研究。为此,作者采用SHPB试验结合有限元模拟方法计算重构了38CrMoAl高强度钢试样的应力-应变曲线,定量分析了端面摩擦因数、子弹入射速度、试样长径比和试样形状对端面摩擦效应引入的峰值应力、应变测试误差的影响。

1 试样制备与试验方法

试验材料为38CrMoAl高强度钢,由东北特殊钢集团有限公司提供,化学成分见表1。制取尺寸为φ5 mm×2.5 mm的圆柱体试样,采用Instron型万能材料试验机、SHPB装置分别进行准静态、SHPB压缩试验,每组试验重复3次取平均值。参照GB/T 7314—2017,准静态试验应变速率分别为10-3,10-2,10-1s-1。SHPB试验应变速率分别为650,1 500,2 000,3 500,5 500 s-1,润滑条件为试样端面涂凡士林润滑剂和不涂润滑剂,试样长径比分别为0.5,0.6,1.0,2.0。

表1 38CrMoAl高强度钢的化学成分Table 1 Chemical composition of 38CrMoAl high strength steel

2 SHPB试验有限元模拟

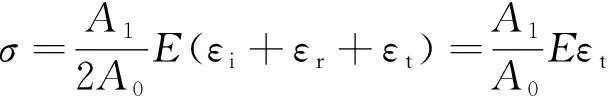
(1)

(2)

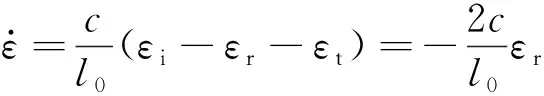
(3)

式中:εi,εr,εt分别为入射波、反射波和透射波应变;A0,l0分别为试样初始端面面积和初始长度;A1为压杆端面面积;E为材料的弹性模量;c为应力波波速。

采用具有应变速率效应的Johnson-Cook(J-C)本构方程描述试样动态力学性能,通过连乘关系描述应变、应变速率和温度T对屈服应力和失效应变的影响[19-21]。J-C方程如下:

(4)

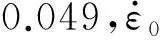
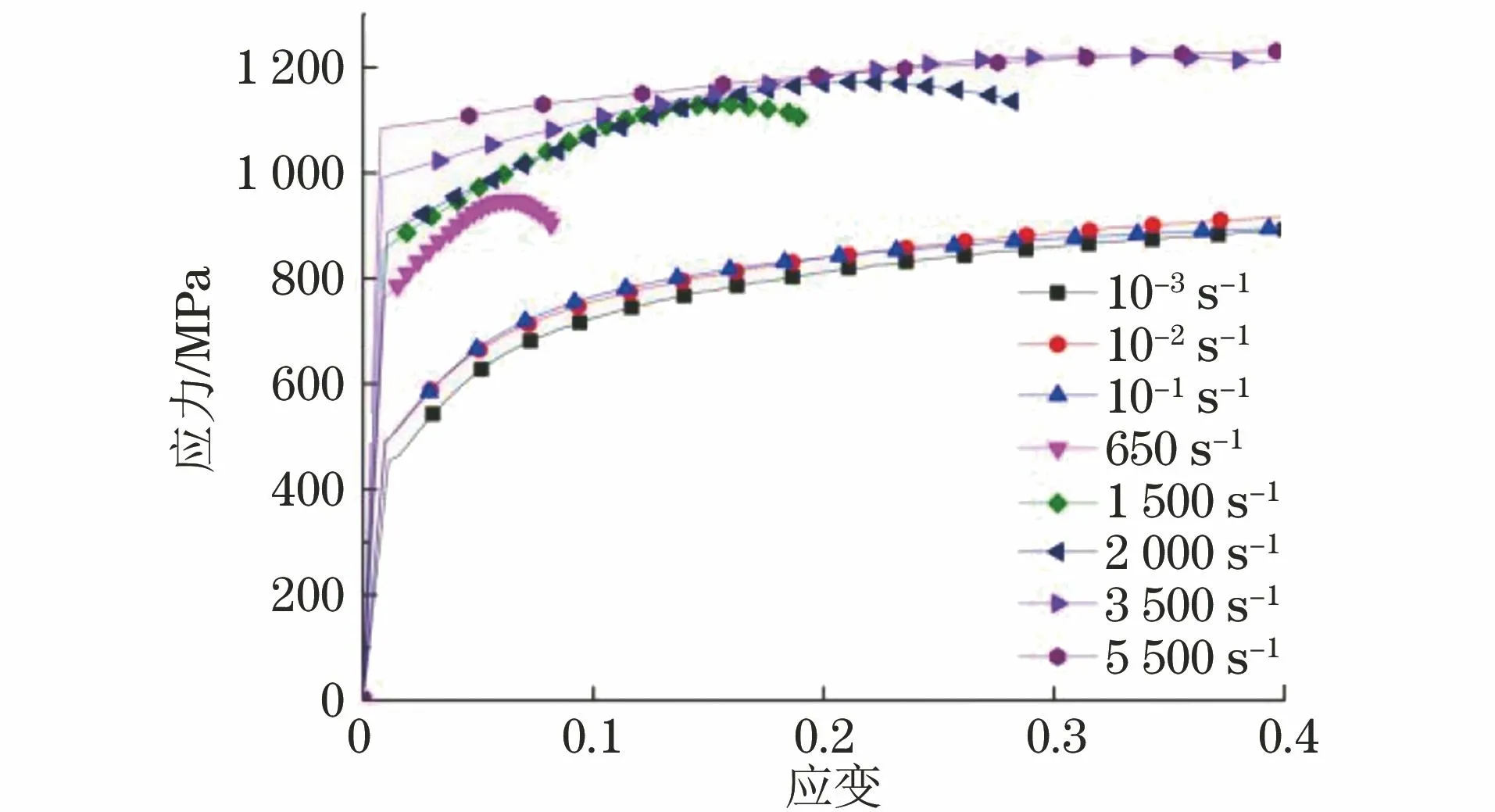
图1 不同应变速率下38CrMoAl高强度钢的应力-应变曲线Fig.1 Stress-strain curves of 38CrMoAl high strength steel under different strain rates

采用ABAQUS有限元软件建立SHPB试验有限元模型。子弹长度为200 mm,压杆(入射杆与透射杆)长度为1 250 mm,子弹与压杆直径均为15 mm。子弹和压杆的制造材料为18Ni钢,和试样的密度均为7 800 kg·m-3,弹性模量均为210 GPa,泊松比均为0.3。子弹、入射杆和透射杆采用六面体网格,网格单元尺寸为1.5 mm,网格单元数为190 332个。试样采用六面体网格,网格单元尺寸为0.2 mm,网格单元数为33 480个。端面接触采用表面与表面接触的罚函数算法。压杆与试样端面之间的摩擦效应采用库伦摩擦模型表征:

σt=μσn

(5)

式中:σt,σn分别为接触面上的切向摩擦力和法向应力;μ为摩擦因数。

通过式(1)、式(2)和式(3)对有限元模拟得到的入射和透射波形进行数据处理,可重构试样SHPB试验的应力-应变曲线。设置子弹冲击速度为30 m·s-1,端面摩擦因数为0.5,试样长径比为0.5,模拟得到SHPB试验中的应力波传播过程如图2所示,可知:t为0时,子弹由气炮装置射出撞击入射杆,在入射杆上产生入射波;t为280 μs时,入射波到达杆件与试样端面,试样开始受力变形;t为350 μs时,试样压缩变形达到最大,随后进入应力卸载阶段;t为560 μs时,应力波到达透射杆的末端,末端应力最大。

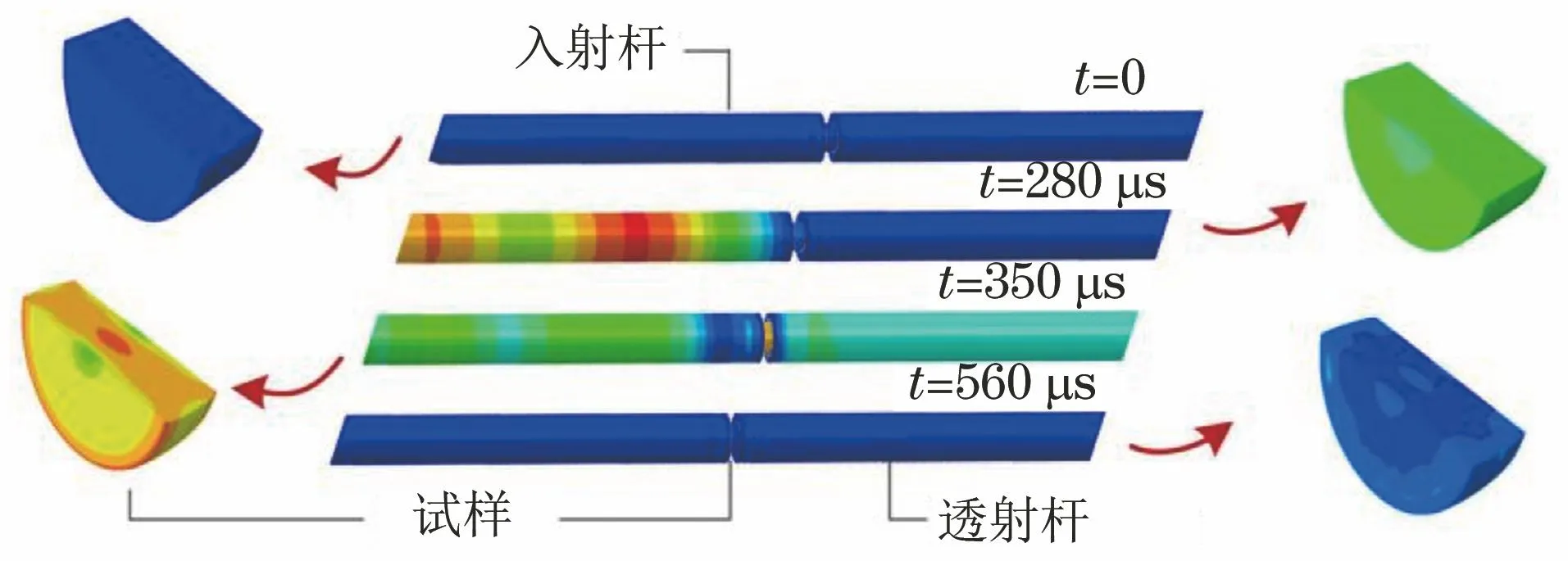
图2 模拟得到SHPB试验中的应力波传播过程Fig.2 Stress wave propagation process of SHPB test

为验证有限元模拟的准确性,取入射杆和透射杆中点作为输出,得到端面无摩擦效应时的入射波和透射波的应变时程曲线,如图3所示。采用二波法对图3进行处理,得到试样真应力-真应变曲线,并与J-C本构方程得到的曲线进行对比。由图4可见,有限元模拟结果与J-C本构方程计算结果一致,表明有限元模拟结果准确可信。

2.1 端面摩擦因数

霍普金森压杆加载时间极短,通常在微秒级,难以通过试验的方法获得端面摩擦因数,可以采用有限元模拟方法,通过调整端面摩擦因数,模拟试样尺寸,将试样尺寸与试验结果对比来确定端面摩擦因数。采用有限元模拟应变速率1 500 s-1下、长径比为2.0的试样在端面润滑与未润滑(摩擦因数0.05)条件下的SHPB压缩过程,得到压缩后试样尺寸,与试验所得试样尺寸进行对比。由图5可见:端面有润滑剂充分润滑时,试样变形后仍然是一个圆柱体,试验和模拟获得变形后试样尺寸分别为φ5.43 mm×8.52 mm,φ5.43 mm×8.51 mm;而无润滑剂时,模拟和试验获得变形后的试样均在中间有鼓形突出,鼓形突出中心的直径分别为5.45,5.51 mm。试验得到变形后试样长度为8.46 mm,两端直径为5.40 mm;模拟获得变形后试样长度为8.47 mm,两端直径为5.34 mm。润滑与未润滑模拟结果与试验结果的相对误差均小于1%,说明无润滑条件下的端面摩擦因数约为0.05。

图5 试验与模拟得到润滑与未润滑条件下冲击变形后长径比为2.0试样的尺寸Fig.5 Test (a,c) and simulation (b,d) sizes of the samples with length-diameter ratio of 2.0 after impact deformation under lubricated (a-b) and unlubricated conditions (c-d)

由图6可见:润滑与未润滑条件下尺寸为φ5 mm×10 mm的试样的应力-应变曲线保持了很好的一致性,屈服强度相对误差小于2%,说明端面摩擦效应可以忽略;尺寸分别为φ5 mm×3 mm,φ5 mm×5 mm试样的应力-应变曲线在有无润滑条件下出现了较大的偏差,屈服强度相对误差达到了10%左右,端面摩擦效应的影响不能忽略。

图6 润滑与未润滑条件下SHPB试验中应变速率为1 500 s-1下不同尺寸试样的应力-应变曲线Fig.6 Stress-strain curves of the samples with different size under 1 500 s-1 strain rate during SHPB test under lubricated and unlubricated conditions

3 结果与分析

3.1 SHPB试验有限元模拟结果

SHPB试验中,子弹入射速度、试样形状和长径比是影响摩擦效应的主要因素。设置6种端面摩擦因数μ(0,0.1,0.2,0.3,0.4,0.5)、3种子弹入射速度v(20,30,40 m·s-1)和2种试样形状(圆柱体,立方体),其中圆柱体试样直径为5 mm,长径比分别为0.25,0.50,1.00,立方体试样边长为5 mm。模拟得到在SHPB冲击过程中试样的应力-应变曲线见图7。

图7 模拟得到不同条件下SHPB试验中不同尺寸试样的应力-应变曲线Fig.7 Simulation stress-strain curves of samples with different size during SHPB test under different conditions: (a-e) cylindrical samples and (f) cube samples

3.2 端面摩擦效应引入的误差

端面摩擦效应引入的峰值应力测试误差eσ[22]、峰值应变测试误差eε计算公式如下:

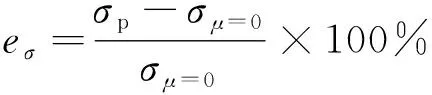
(6)

(7)

式中:σp,εp分别为数值模拟得到的试样峰值应力和峰值应变;σμ=0,εμ=0分别为端面无摩擦时试样的峰值应力和峰值应变。

将图8得到的峰值应力和峰值应变分别代入式(6)和式(7),计算得到不同条件下的测试误差。由图8可知:试样的峰值应力和峰值应变测试误差均随端面摩擦因数的增大而增大,但误差增长幅度逐渐减缓;随着子弹入射速度增加,峰值应力测试误差增大,而峰值应变测试误差减小,当端面摩擦因数较大时,控制子弹速度不能有效减小端面摩擦效应带来的试验误差;峰值应力和峰值应变测试误差均随试样长径比的增加而减小,且长径比对峰值应力测试误差的影响要小于对峰值应变的影响;当端面摩擦因数控制在0.1以内时,长径比大于0.50的圆柱体试样峰值应力和峰值应变测试误差均小于10%,摩擦效应小,这与试验结果以及文献[11,23]中的结论一致;端面摩擦因数为0.1～0.5时,长径比大于1.00的圆柱体试样的峰值应力、峰值应变测试误差均小于10%。因此,对试样端面进行一定程度的润滑,使端面摩擦因数降到0.1以下,或是选用长径比为1.0以上的试样,均可以有效降低端面摩擦效应对SHPB试验结果的影响。但是长径比太大时,试样达到应力均匀状态的时间将变长,不利于保持试样的径向加载。圆柱体试样的峰值应力、峰值应变测试误差略小于相同截面面积的立方体试样,两者相差小于2%,因此试样的两种不同形状对于端面摩擦效应引入的测试误差影响很小。

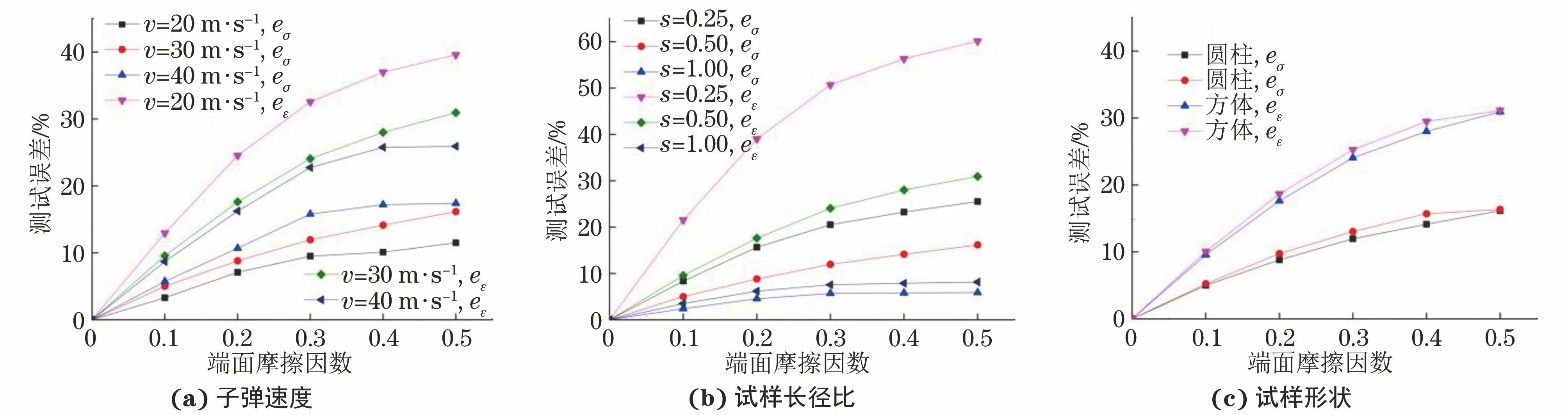
图8 不同条件下试样的峰值应力、峰值应变测试误差随端面摩擦因数的变化曲线Fig.8 Peak stress and peak strain test errors vs interface friction cofficients of samples under different conditions: (a) bullet velocity; (b) length-diameter ratio and (c) shape

4 应力波传播分析

SHPB系数端面摩擦效应加载示意如图9所示,图中:As为试样截面积;σ1为所受应力;A2为右端面积;σ2为所受应力;R为端面半径;ΔR为半径差值;Δl代表试样轴向一个趋于无穷小的段。

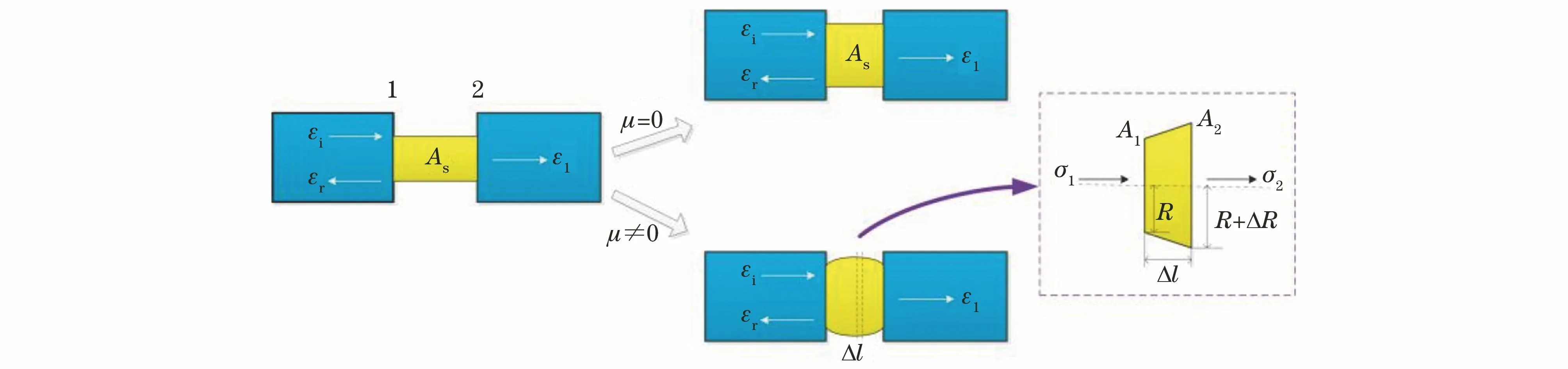
图9 SHPB系统端面摩擦效应加载示意Fig.9 Schematic diagram of friction effect loading of SHPB system

试样1,2两端面的应变分别为ε1,ε2,则两端面的位移u1,u2满足

(8)

ε1由入射脉冲和反射脉冲产生,ε2仅由透射脉冲产生,由三波脉冲产生的试样平均应变为

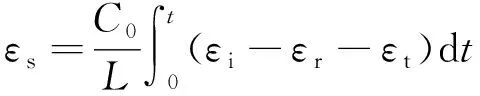
(9)

式中:L为试样长度。

端面1、2处的载荷分别为

P1(t)=EA[εi(t)+εr(t)]

(10)

P2(t)=EAεt(t)

(11)

式中:E为压杆弹性模量;A为压杆端面面积。

应力波数据处理方法基于一维应力波理论与应力均匀化假设,当端面无摩擦时,应力波从入射杆传入试样,并在试样中经过数次反射,使试样内部达到应力均匀。由于试样长度相对较短,满足应力均匀化所需的时间极短,可以认为试样满足应力均匀化假设,即满足

εi+εr=εt

(12)

将式(12)代入式(1),可得

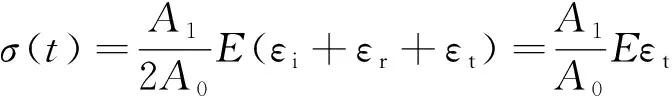
(13)

试样与压杆端面由于摩擦限制不能自由滑动,变形时试样的横截面沿轴向变化形成鼓形。对于试样轴向一个趋于无穷小的Δl段,由应力平衡条件可得

σ1·A1=σ2·A2

(14)

Δl趋于无穷小时,两端面A1和A2的半径差值ΔR也趋于无穷小,忽略高阶项可得

(15)

当端面存在摩擦时,应力波在试样中的传播受到截面面积变化的影响,试样内部应力分布不均匀,试样的横截面积不再是一个恒定的值,此时不满足应力均匀化假设,SHPB数据处理结果出现误差。

文献[24-25]从能量守恒定律出发,推导出端面摩擦的修正公式,认为摩擦效应与端面摩擦因数、试样长径比有关,公式如下:

σz=σ0+Δσf

(16)

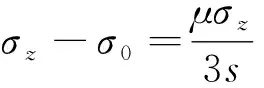
(17)

式中:σz为平均轴向应力;σ0为屈服应力;Δσf为端面摩擦引起应力增值。

由式(1)～(3)可知,当子弹入射速度一定时,不同端面摩擦因数下压杆中的入射波是不变的,而反射波和透射波决定了试样最终的应力-应变曲线。试样端面在不同摩擦因数下的反射波和透射波应变时程曲线见图10,可知随着端面摩擦因数增大,反射波应变增大,透射波应变减小。随着端面摩擦因数增大,由应力波数据处理计算得到试样应力将增大,应变将减小,与图8相吻合。

图10 不同端面摩擦因数下圆柱体试样的反射波和透射波应变时程曲线Fig.10 Strain time history curves of reflected (a) and transmitted (b) wave of cylindrical sample under different interface friction coefficients

由图11可知:试样内部应力沿轴向和径向分布均不均匀,中部和端面边缘处应力较大,这是因为在摩擦力作用下试样横向变形受到限制,使靠近端面边缘处应力增大,应力均匀性被破坏;随着长径比增大,应力集中部位占试样总长度比例减小,端面摩擦效应的影响减小,这是因为长径比较小的试样端面摩擦造成的横向变形区域占试样的比例较大。

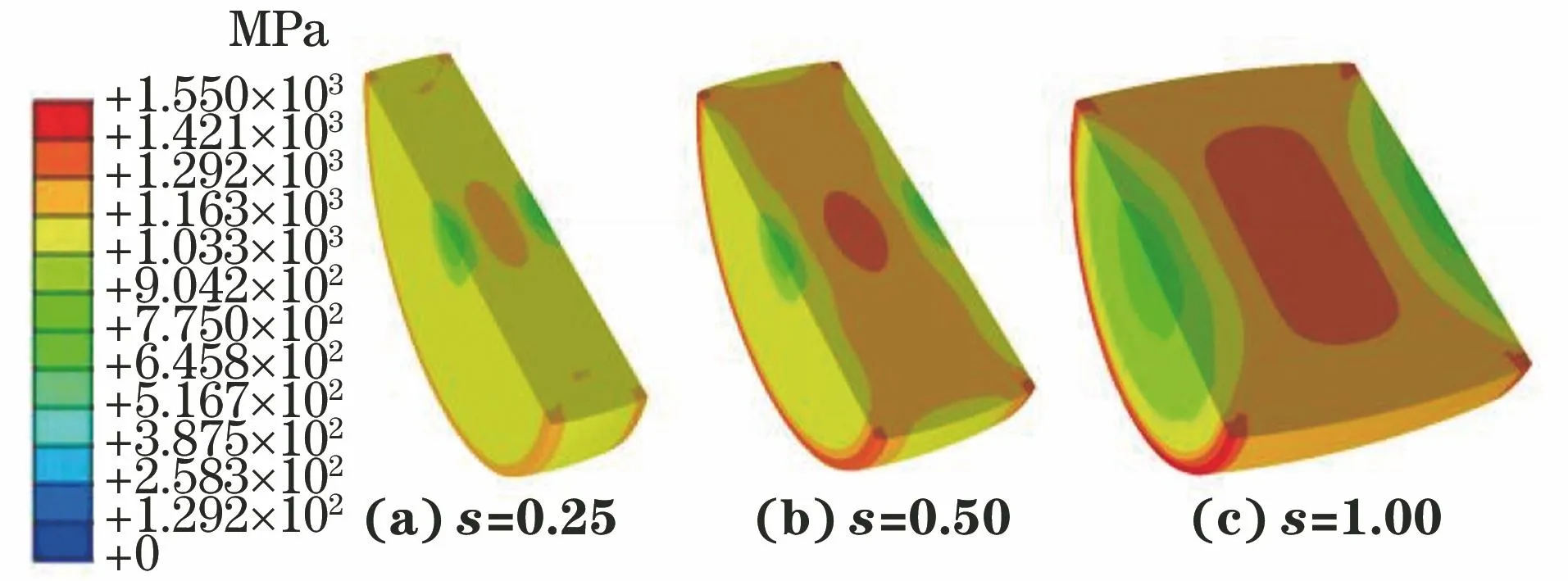
图11 冲击速度为30 m·s-1下端面摩擦因数为0.5时不同长径比圆柱体试样的变形应力云图Fig.11 Deformation stress nephogram of cylindrical samples with different length-diameter ratios under impact rate of 30 m·s-1, interface friction coefficient of 0.5

由图12可见,截面面积相同的圆柱体和立方体试样的应力分布基本一致,立方体试样的应力集中稍大于圆柱试样。这与应力-应变曲线的误差分析一致。

图12 冲击速度为30 m·s-1下端面摩擦因数为0.5时截面面积相同的圆柱体与立方体试样的变形应力云图Fig.12 Deformation stress nephogram of cylindrical (a) and cube (b) samples with the same section area under impact rate of 30 m·s-1, interface friction coefficient of 0.5

在圆柱体试样端面和侧面处取4个点,在同截面面积立方体试样上取5个点,如图13所示,各点的应变时程曲线如图14所示,可知:圆柱体试样端面边缘C点处应变最大,端面中心A点处应变最小;B点和D点处应变在试样受压阶段时相差不大,进入卸载阶段后B点应变趋近于0,A点、C和D点均保持残余应变;立方体试样端面顶点E′点处应变最大,端面中心A′点处应变最小,除E′点外,各点的应变均略大于圆柱体试样相应点的应变;圆柱体试样和立方体试样在端面边缘的应变均最大,立方体试样边缘点由于距离试样中心更远,其应变也更大。

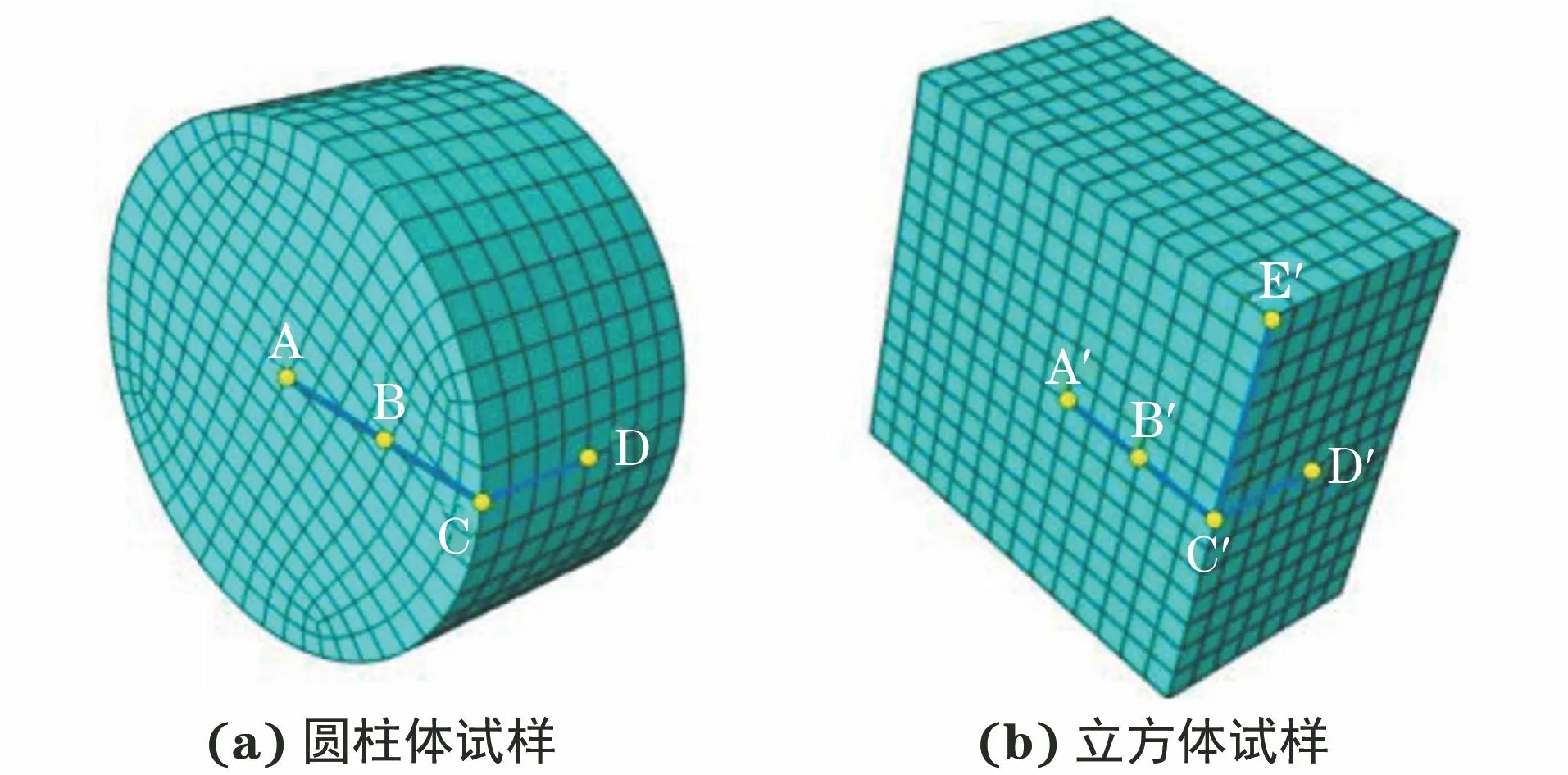
图13 圆柱体与立方体试样取点位置Fig.13 Points on cylindrical (a) and cube (b) samples

图14 圆柱体和立方体试样上各点的应变时程曲线Fig.14 Strain time history curves of points on cylindrical and cube samples

5 结 论

(1) 38CrMoAl高强度钢试样由端面摩擦效应引入的峰值应力、峰值应变测试误差随端面摩擦因数的增大而增大,但增大幅度逐渐减缓;测试误差随长径比的增加而减小,且长径比对峰值应力测试误差的影响要小于对峰值应变的影响;截面面积相同的圆柱体和立方体试样的测试误差小于2%,无显著差别;端面摩擦因数较大时,控制子弹入射速度不能有效减小端面摩擦效应带来的试验误差。将试样端面摩擦因数降到0.1以下,或是选用长径比1.00以上的试样,均可以有效降低端面摩擦效应对SHPB试验结果的影响。

(2) 模拟得到端面摩擦效应破坏了试样内部的应力均匀状态,试样中部和端面边缘处应力最大;随着试样长径比增大,端面应力集中部位占试样总长度比例减小,端面摩擦效应的影响减小,与端面摩擦效应试验结果一致。