改进GA-RBF 神经网络的水厂混凝投药预测

刘海林, 王庭有

(昆明理工大学机电工程学院, 云南 昆明650500)

净水投药作为整个净水处理生产的核心工艺之 一,在投药过程中存在复杂动态非线性,难以建立一个精确的模型来预测混凝剂投加量。 因此,实现投药量的最佳控制,保障出厂水质达标和提高经济效益,是现阶段净水工艺的重要研究方向[1-2]。 针对投药过程中的高度非线性的特点,韩梅等[3]、饶小康等[4]采用人工神经网络算法从历史投药数据进行自适应学习和训练并与自动化系统结合实现混凝投药自动化控制系统。 OLADIPUPO 等[5]、张瑶瑶等[6]结合自来水厂进水指标影响因子,通过多模型预测控制策略、混凝分析计算,构建线性回归模型和机理模型,进行投药量预测,提高了投药量的精确度,但线性回归模型和机理模型均需要满足影响因子的动态稳定,计算方式复杂冗余且对数据的要求苛刻,难以全面推广。 黄丽娟等[7]、唐德翠等[8]、徐洋等[8-9]通过BP 神经络模型结合专家经验对混凝投药进行辨识建模,然而单一标准BP 神经网络预测模型对复杂非线性动态投药自适应学习能力较差,预测效果有较大偏差,模型性能受到制约。 余峰等[10]、李赞等[11]采用遗传算法(GA)或烟花爆炸算法优化了BP 神经网络预测模型建模缺点,极大提高了BP 神经网络模型在全局范围内寻优能力以及对水质动态复杂投药的自适应学习和预测效果,但BP 易陷入局部极小值,导致存在误差,稳定性不高,使预测误差增大。 徐少川等[12]提出模糊算法优化多小脑神经网络,更精确地将浊度控制在控制范围内,进一步优化投药量,提供了良好优化思路。 庹婧艺等[13]采用改进RBF 神经网络有效规避了BP 神经网络缺陷,提高了模型的泛用能力。

通过改进GA 算法适应度,优化函数提高鲁棒性和并行计算能力,优化神经网络的权值和中心宽度向量参数的寻优效率,能更好的达到模型预期的目标值,精确预测效果和检验所建立GA-RBF 模型对水质预测数据拟合能力[14]。 本文采用改进RBF神经网络模型,通过进水水质指标与投加量的非线性规律,建立GA-RBF 神经网络净水厂投药量预测模型。 GA-RBF 算法的应用有助于减少资源浪费和提高水质处理的效率,实现更加有效的药剂使用和资源配置,减少过量投药或不足投药的现象,可以降低成本并提高生产效率。 同时,该模型可以更准确地预测水质变化趋势,帮助净水厂及时调整投药量和水质管理策略,避免因水质问题导致的损失,提高净水厂运营的稳定性和可靠性。

1 GA 优化RBF 神经网络预测模型建模

1.1 RBF 神经网络

RBF 神经网络是一种特殊的三层前馈式神经网络,包含输入层、隐含层和输出层的简单拓扑结构,具有核函数转置映射到高维度线性空间的非线性样本特征,直接用网络的权值求解线性方程组来转化输出的特性。 RBF 神经网络可全局逼近任意非线性函数,搜索功能精度更高,可以回避局部极值问题[15],具有良好的局部逼近能力的高斯核函数常作为维度激活函数,在输入层映射到隐含层的一系列径向基函数中使用,其表达式(1)如下[13]:

式中,x为网络输入向量;ri为高斯基函数中心向量;σi为高斯基函数宽度向量。

RBF 神经网络输出的表达式如式(2)[13]:

式中,f(x)为网络输出预测值等于隐含层所含各节点输出与权值的乘积之和;wi为隐含层至输出层之间的权值。

混凝沉淀所关联的影响因素很多,基于水质检测指标之间数据高度非线性的特点,通过前人分析各因素对混凝剂投加量的影响程度及现场水厂调查,最终确定8 个指标作为RBF 网络的8 个工艺输入参数维度[16],分别为原水水质指标中的水温、电导率、pH、CODMn、原水浊度和进水量Q,沉淀池加药反应出水滞后时间和滤前水浊度,建立以混凝剂投药量为RBF 网络的输出参数维度[17]的RBF 神经网络结构,见图1。

图1 RBF 神经网络结构Fig.1 Structure of RBF neural network

在RBF 神经网络中,通常选用K均值聚类法求得最佳聚类数K值,用来确定隐含层神经元高斯径向基函数的中心,进一步优化RBF 神经网络结构和对数据进行重新分类,因此,可通过聚类数K值推导隐含层最佳神经元个数。 对输入特征参数数据集x(x1,x2,x3,x4,x5,x6,x7,x8)进行数据预处理归一化转置到隐含层中,并随机选取所设定的K个固定中心点见式(3)。

高斯基函数方差μ表达见式(4)[16]。

式中,Smax为各中心点之间的最大距离;N为神经网络隐含层神经元总节点数。

其中,损失函数大小可对应聚类结果的好坏,因此,损失函数可定义为各输入特征参数数据集样本到所属的ρK簇中心点距离差的平方和,见式(5)[16]。

式中,xi为第i组数据集样本;Ki为xi数据集所属的簇;ρK为Ki簇对应的中心点。

通过调整损失函数第一次所得不同数据集样本xi对应分配到距离最近所属类别的ρKi中心点,然后重新聚合计算该类中心,再调整中心点继续减少损失函数值,反复迭代。 当满足时,即停止迭代,此时,损失函数递减到极小值且满足中心点的变化收敛条件,得到最佳聚类数K值。

1.2 GA 优化RBF 神经网络

遗传算法是以种群的形式进行交叉、选择和变异等过程,经过多代遗传进化获得适应度最优的个体作为目标值最优解的一种自然规律演化优化算法[18],在全局范围内具有较强的搜索能力。 由于RBF 神经网络可通过局部逼近进行累加从而实现全局逼近,具有较强的泛化能力,但对神经网络的参数优化有较高要求,因此,本文采用GA 优化RBF神经网络的隐含层至输出层之间的权值wi和高斯基函数中心宽度向量σi两种参数进行优化提高神经网络的效率和训练精度,从而提高对投药量变化趋势精准预测。 当种群适应度值满足进化精度要求或遗传算法达到进化迭代收敛上限次数时,即输出遗传优化之后的隐含层至输出层之间的权值wi和高斯基函数中心宽度向量σi两种参数并映射转换更新RBF 神经网络结构和参数,改进GA 算法优化流程见图2。

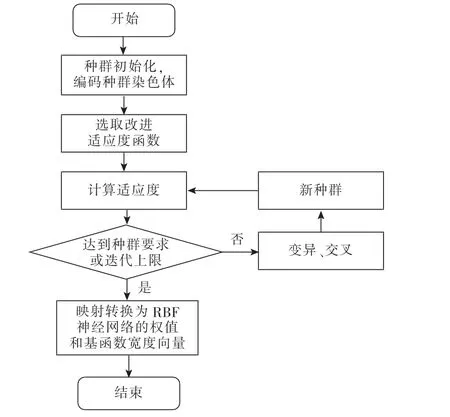
图2 改进GA 算法优化流程Fig.2 Improve GA algorithm optimization process

GA-RBF 神经网络主要优化步骤如下:

(1)染色体编码优化

本文采用gray 二进制编码方法随机将RBF 神经网络中初始高斯基函数宽度向量σi和权值wi两个优化参数染色体转换为对应的二进制混合编码并对转换后的二进制数值进行异或操作得到新的数值生成特殊gray 二进制编码,该方法简单易行且符合最小字符集编码原则[19],对于离散性变量可以直接进行编码,同时在编码转换过程中只有一位的变化,避免了普通二进制编码中的不连续性问题,在执行交叉和变异操作时可以缩减多余的解空间,提高算法的计算效率。 设初始种群规模数量为P,则编码每代新种群的染色体见式(6)。

(2)改进适应度函数

基因误差参数选取为RBF 神经网络对应的第i个遗传因子的期望输出与实际输出的差值的绝对值的平方和,即式(7)[19]。

令种群中第i个遗传因子适应度函数为常数与ei基因误差参数差值的倒数,当ei误差逐渐减小时,遗传因子适应度逐渐收敛至极小值,得到的染色体越优秀[20],通过对适应度值进行缩放,使适应种群的个体获得更大的选择概率并通过添加惩罚函数策略对适应度值进行优化避免模型存在过拟合的问题,即改进得到的适应度函数见式(8)。

(3)遗传操作优化

采用赌轮盘法对种群P进化择优,则该种群中随机选其中第i个遗传个体的概率见式(9)。

通过赌轮盘法初步选择操作后,即开始对该类父代个体进行初始自适应交叉、变异得到新一代子代个体,其中自适应交叉概率和变异概率均会随子代种群的适应度不断改变,优化变异操作引入了随机性,保持了个体的多样性以控制多样性和局部搜索的平衡,得到初始交叉概率、变异概率和子代新交叉概率、变异概率关系见式(10)～式(11)[19-20]。

式中,Pa为交叉概率;Pa1为初始交叉概率;Pa2为新交叉概率;Pb为变异概率;Pb1为初始变异概率;Pb2为新变异概率;Favg为种群平均适应度;Fmin为种群收敛最小适应度。

两个变异子代个体是在经过优化筛选的父代种群中随机选取两个父体进行交叉选择和变异择优选择得到的,将变异子代染色体与父代染色体的适应度进行比较,如果子代适应度优于父代,则将子代与父代替换编入种群P中成为新种群进行反复迭代进化,通过交叉和变异所得两个子代染色体表示为式(12)[20]。

式中,λ为(0,1)任意实数。

其中每个种群个体可以作为一个独立的计算单元在交叉和变异过程中进行并行计算优化,实现多目标并行优化,从而缩短搜索过程。 通过精英保留策略,将适应度最优的个体保留至下一代,保持种群的进化优势同时这个过程不受随机选择的限制,直接得到最优选择个体。

2 试验数据采集与仿真

2.1 试验数据采集

为了获得样本数据用于构建预测模型,本试验数据采集自四川某自来水厂不同时段水质监测站的自动监测数据,采集该自来水厂2022 年3 月至2023年3 月共1 263 组相关非线性因素影响指标参数以及相应时段调控实际混凝剂投加量数据,其中1 220组作为训练集和43 组作为测试集,见表1。

总而言之，高效课堂是新课程标准改革形势下教师的一种新的教学理念，更是判断教师授课质量的评判标准。因此，高中政治教师应为学生构建轻松、和谐的课堂学习氛围，从而构建高效的高中政治课堂。

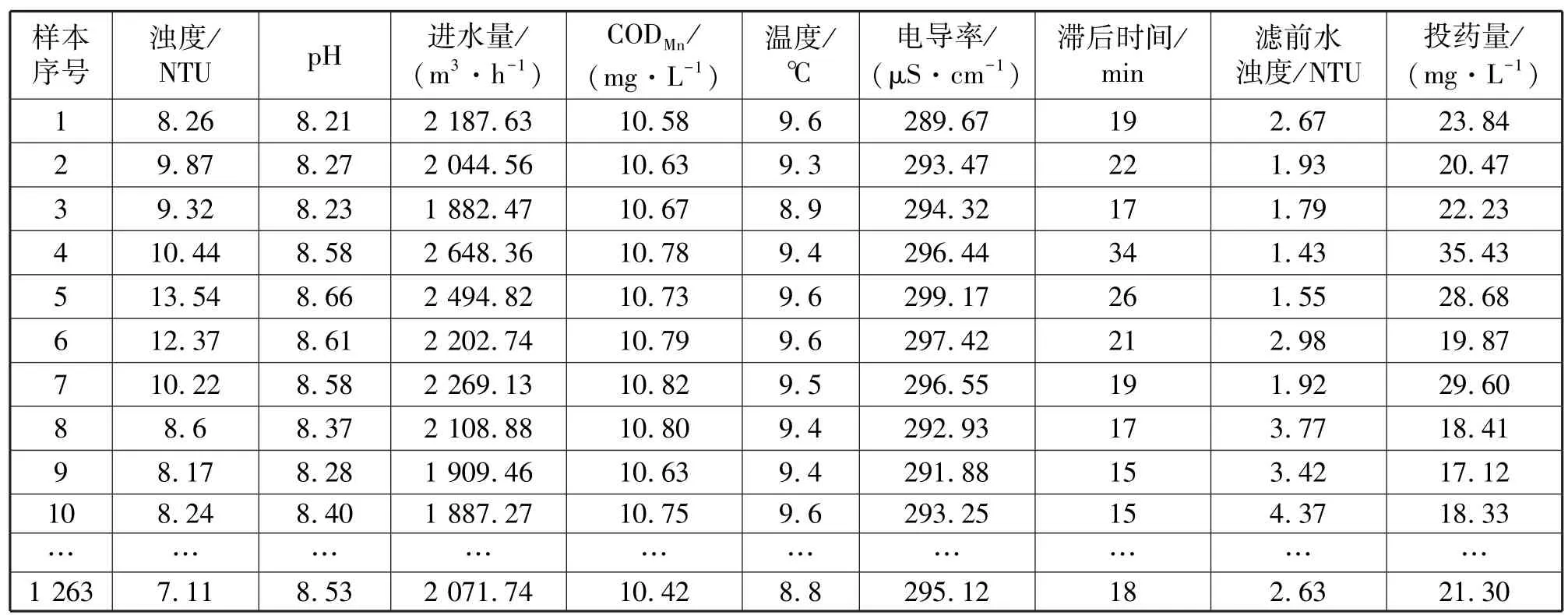
表1 试验数据样本采集Tab.1 Collection of experimental data samples

2.2 仿真分析

2.2.1 运行结果

本文仿真采用Matlab 软件进行神经网络搭建和相应遗传优化,经计算,当遗传算法中的初始种群规模P设为30,最大进化代数设为200,最佳交叉概率Pa设为0.75,变异概率Pb设为0.24 时,该自来水厂模型当神经网络中聚类数K值为9,隐含层的高斯基函数各类簇的方差最优,即隐含层结构神经元最佳个数l也为9,所得混凝剂投加量预测结果均方误差(MSE)为0.193%,进化代数43 代开始收敛,仿真计算得到测试集数据的拟合优度R2为0.984 61,平均绝对误差(MAE)约为2.184%,根均方误差(RMSE)约为4.878%,平均绝对百分比误差(MAPE)约为0.126 49%。 得到的改进GA-RBF 神经网络净水厂投药量预测模型对水厂优化预测结果见图3,混凝剂投加量预测结果优秀,该自来水厂的拟合优度R2值趋近1,模拟预测精度高。

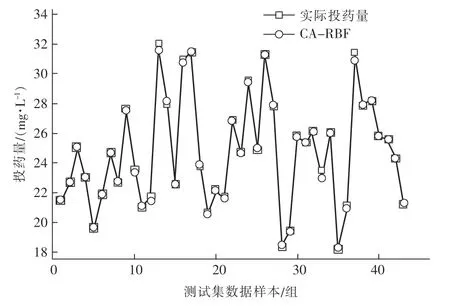
图3 改进GA-RBF 神经网络预测结果Fig.3 Improved GA-RBF neural network prediction results

2.2.2 性能分析

改进GA 优化的RBF 神经网络进化代数在43代就能完成收敛,而单一的RBF 神经网络则需要进化149 代才能完成收敛,两种模型适应度曲线对比见图4。 通过改进GA 优化的RBF 神经网络,遗传进化代数明显降低,预测模型运行速度更快。

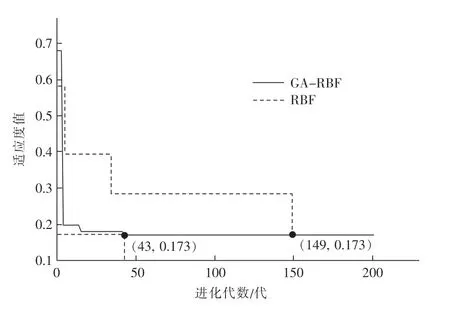
图4 改进GA-RBF 与RBF 神经网络适应度曲线对比Fig.4 Comparison of fitness curves between improved GA-RBF and RBF neural networks

由图5 可知,改进GA-BP 神经网络模型在全局学习预测效果一般,容易陷入极小值陷阱且模型的稳定性不高,单一RBF 神经网络模型所预测的结果与实际药剂投加量有较大误差,拟合能力较差,搜索的精度不高,而改进GA-RBF 神经网络模型优化明显优于前两种神经网络模型,其精度更高,稳定性强,对数据有更好地拟合能力,且通过比较PSORBF 模型预测效果可知,GA-RBF 模型在预测解空间的并行计算能力和鲁棒性比PSO 优化的模型具有更好的优势。

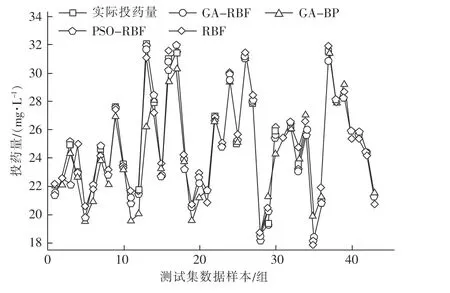
图5 不同算法预测效果对比Fig.5 Comparison of prediction effects of different algorithms

改进GA-RBF 神经网络相较于单一RBF 神经网络,混凝剂投药量预测拟合优度提高5.474%,平均绝对误差降低了4.14%, 根均方误差降低3.392%,且对比其他两种优化的神经网络具有更高的模拟精度,能有效预测自来水厂混凝剂投加量,网络模型参数对比见表2。

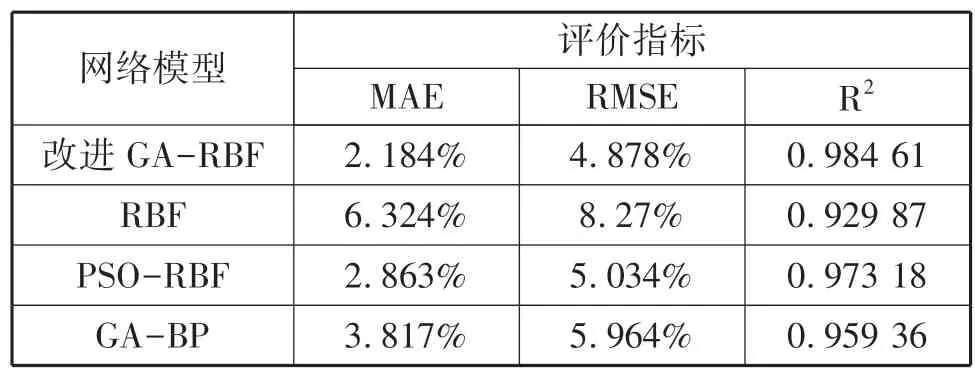
表2 网络模型参数对比Tab.2 Comparison of network model parameters

3 结论

本文将改进GA 算法与RBF 神经网络模型相结合,提出一种改进GA-RBF 神经网络优化预测模型,解决自来水厂混凝剂投加量预测控制问题,其仿真结果表明:

① 本文提出的GA 算法优化后的RBF 神经网络预测模型回避了GA 优化BP 神经网络易陷入极值陷阱的缺点,提高了稳定性和全局寻优能力,对数据有更好的拟合能力。

② 水质影响因素特征参数和投药量之间的高度非线性关系可直接由RBF 神经网络的径向基函数转换并通过网络线性输出,满足了影响因子的动态稳定,对数据没有过多的要求,减少了对复杂模型的构建和冗余计算。

③ 在水厂投药量预测模型预测效果参数对比中,GA 算法优化RBF 神经网络净水厂投药量预测模型的MAE 约为2.184%,RMSE 约为4.878%,R2为0.984 61,相较于单一RBF 神经网络预测模型迭代速度更快、预测精度更高,并且相较于PSO-RBF模型预测效果,GA-RBF 模型对解空间的鲁棒性和并行计算能力更具优势,可为水厂混凝投药预测模拟提供有效参考。