高压油管压力控制问题的微分模型与求解

徐兴波

（淮阴工学院 数理学院，江苏 淮安）

喷射系统是燃油发动机的重要部件，如何保持高压油管内的压力稳定是提高燃油效率的关键。在喷射系统中，雾化低压燃油经由凸轮控制的高压油泵压缩为高压燃油，再在压力差的作用下通过单向阀涌入高压油管，而高压油管有若干个由针阀控制的锥型喷油器来进行喷油，这一动态过程被描述为高压油管压力控制问题，即2019 年高教社杯全国大学生数学建模竞赛A 题，见图1。建模竞赛题有三个子问题，已有不少文章就该赛题进行了研究[1-2]，但该问题仍然值得进一步细化讨论。

图1 具有减压阀和两个喷油嘴时高压油管示意（源自赛题）

需要厘清三个方面的函数关系：(1) 弹性模量E(P)和压力P 之间的关系，进而精确给出燃油密度ρ(P)和压力P 的关系；(2) 针阀运动hz(t)与时间t 的关系，进而给出喷油截面积Sp(t)与时间t 的关系；(3) 凸轮极径r(θ ) 与极角 θ之间的关系，进而描述柱塞上下运动速度与时间的关系，也能导出柱塞腔的体积Vh及其变化率。对E(P)的拟合，陈兴志等(2019)[3]用指数函数，何雅宁等(2019)[4]、宋常修等(2021)[5]、王一等(2021)[6]、赵泽宇等(2020)[7]均用多项式函数。杨晓琪等(2021)[8]、毛睿昕等(2022)[9]用数值定积分计算燃油密度，侯超钧等(2021)[10]用了线性插值的方法计算E(P)。本文用二次多项式拟合E-1(P)，拟合精度好于之前结果，而且可以给出燃油密度的计算公式。何雅宁等(2019)对针阀升降程运动曲线采用高斯函数拟合，本文稍有改进。蔡志杰(2020)[11]给出了赛题评价，但连续模型忽略了补充的低压燃油。本文完善了连续模型并基于python 编程给出了合理的最优解。

在模型建立前，做如下假设：(1) 燃油在高压油管中近似为一维无粘性可压缩理想流体，对高压油管的形状不产生影响；(2) 不考虑能量损失，燃油质量守恒；(3) 喷油器将燃油喷向气缸，气缸压力不低于标准大气压。

1 函数拟合

1.1 燃油密度

数值发现，即便用关于P 的三次多项式或分段函数来拟合弹性模量E(P)，所得结果也不十分理想。根据经验公式，燃油的压力变化量与密度变化量满足，得到关于E(P)的定积分，这启发用多项式来拟合E-1(P)，并且可以得到实用公式：

其中P=100 MPa， ρ= ρ (P) =0.850mg/mm3，且。对E(P)的二次多项式拟合可以采用基于最小二乘法的思想，在基于python 的具体实现上，可以scipy 库中的optimize.leastsq 命令，拟合参数a≈ 6.492165×10-4，a≈-2.005 134×10-6，a≈1.180684×10-9，拟合值与原数据误差均值为10-20量级、方差为10-14量级，拟合效果可以从图2 中看到。另外，在几种压力值下的燃油密度是需要求出的，计算结果为 ρ (P= 0.5)≈ 0.804536，ρ(P= 150)≈0.867920，ρ (P= 160)≈0.871110。

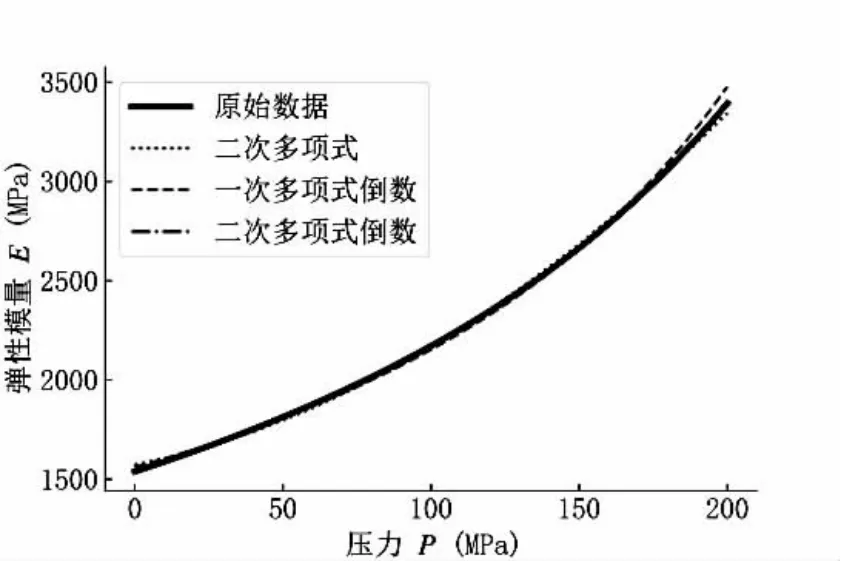
图2 弹性模量E(P)与压力P 的函数关系拟合效果

1.2 凸轮运动

可以利用附件数据绘出凸轮极径r 和极角θ 的函数图像，另外根据x=rcosθ 和y=rsinθ可以绘出凸轮的形状，可以看出凸轮的轮廓是光滑且轴对称的，同时可以计算出极径最大值rmax和最小值rmin之差为4.826 mm。利用python 命令optimize.leastsq 来对r(θ )进行6 次多项式拟合，拟合误差的均值为10-11量级而方差为10-6量级，尽管这样的拟合精度已经不错，但仍不够理想，用更高阶多项式又显得复杂。凸轮曲线类似三角函数余弦曲线，利用函数

拟合可得到更好拟合精度，拟合误差均值为10-16量级且方差为10-10量级。公式(3)既精确又简洁。凸轮曲线和拟合曲线可见图3。

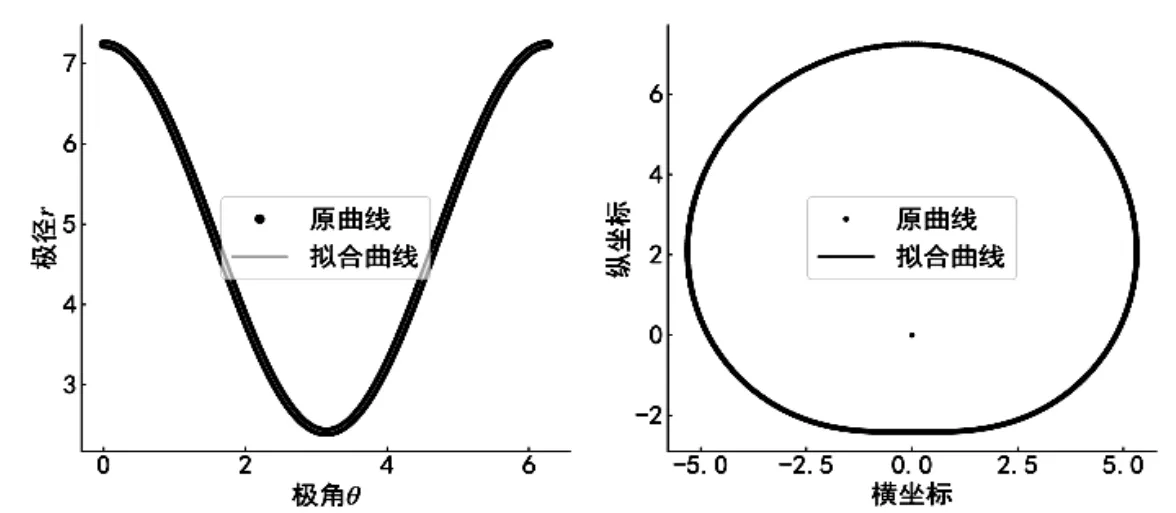
图3 凸轮曲线和拟合曲线

凸轮上边缘顶着柱塞。以凸轮中心为坐标原点，竖直向上方向为正方向，建立一维坐标系。令θ (t) =ωt且 θ (0) =0，凸轮的最长极径在初始时刻竖直向上。凸轮的转动使得竖直方向的极径周期地变化，进而影响着柱塞的周期运动。柱塞的运动幅度即上下止点的距离为4.826 mm,上止点的速度为，这也导致柱塞腔体积Vh有所变化。关于Vh的计算，将在1.4 节给出。

1.3 针阀运动

针阀运动函数Z(t,t0)可以写成分段函数，升程和降程函数虽然可以利用关于时间的多项式来拟合，但利用高斯形式函数来拟合更有效。高斯函数在概率论中是用来描述正态分布密度函数的，本文采用如下形式的函数来拟合针阀升降程运动：

其中t0≥0表示针阀开始升程运动起始时间，也是开始喷油的时刻。赛题所提供的数据对应于t0=0，利用python 命令optimize.leastsq 拟合升程阶段函数z1，得args 为(2.02894068,0.45660788,0.02822825,-0.0067 0365)；拟合降程阶段函数z2，得atgs 为(2.02932375,1.99283185,0.02823941,-0.00670779)。这两个拟合函数的误差均值、方差分别为10-10和10-5量级。当然，令c2分别为0.45 和2.0, 然后再做最小二乘拟合也是可以接受的。

在喷油时间2.45 ms 范围内的针阀运动数据绘图及其拟合曲线在图4 中可见。针阀运动函数Z(t,t0)可以按五种情形来分段定义。(1) 在开始喷油之前，有t＜t0，得Z(t,t0) ≡ 0。在喷油时间段内，有t≥t0，令= mod(t-t0,Tz)和args=(c1,c2,c3)，其中Tz=100 ms 为针阀运动周期;（2） 如果∊ [0,0.45)，Z(t,t0)=z1(,args)；（3）如果 ～t∊[0.45,2.0)，Z(t,t0) ≡2；（4） 如果∊[2.0,2.45)，Z(t,t0) =z2(,args)；（5）如果∊[2.45,100.0)，则Z(t,t0) ≡0。

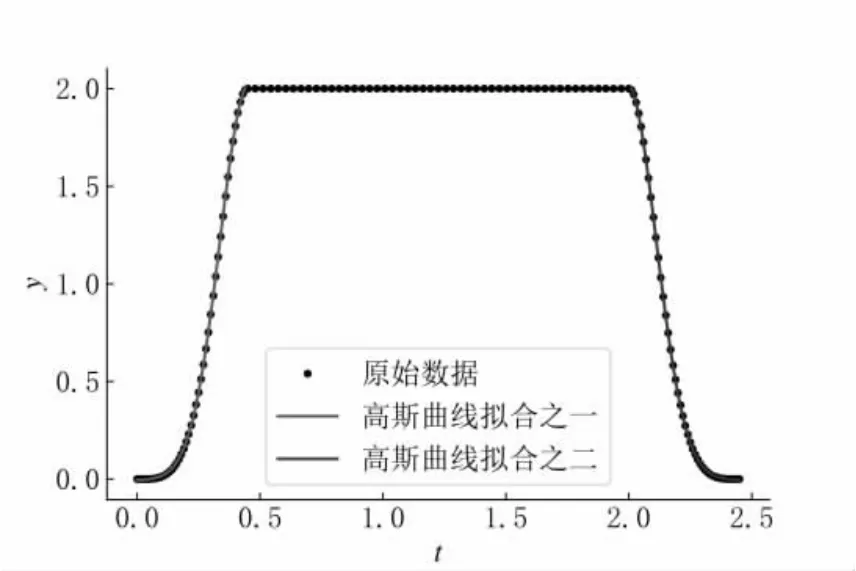
图4 针阀运动数据绘图及其拟合曲线

1.4 燃油流量

燃油注入和喷出的流量实际是单位时间(ms)内进出高压油管的燃油体积，赛题提供了经验公式，也可参考蔡志杰(2020)。从单向阀注入高压油管的高压燃油压力为Ph、密度为 ρh，而高压油管内的燃油压力为Pg、密度为 ρg。记单向阀入口处的截面积为Sa= 0.49π。那么，当单向阀开启时注入高压油管的燃油流量为

当单向阀关闭时，Qin≡0。

2 微分模型

2.1 子问题一

质量等于密度乘以体积，那么单位时间内高压油管内燃油质量的变化等于进入和喷出燃油的流量差，又由于高压油管体积恒定，便可以得到密度对应的微分方程，再根据压力与密度之间的微分方程关系，最后得到关于高压油管内燃油密度和压力的一阶常微分方程组：

初值为 ρ0= 0.850，P0=100。第一个问题是如何选取未知参数Ta和t0使得压力尽可能稳定在100 MPa。为此，需要对方程组(5)进行数值积分，得到节点数为N 的解向量，目标函数为

第二个问题是，如何控制Ta和t0，使得经过T 毫秒时间，压力尽可能稳定在150 MPa。可以使用两阶段的调整策略。首先，调整参数，对方程组(5)数值积分T 毫秒，使得

其次，使用针对第一问的方法，在目标函数(6)中令P0=150，采用数值优化方法求出参数，使得压力尽量维持在150 MPa。

2.2 子问题二

初值满足 ρ= ρ= 0.850， = =100。该方程组含有 ω和t0两个未知参数，问题是确定这两个参数使得高压油管内的压力稳定在100 MPa 左右。对方程组进行数值积分，时间为T，节点数为N，在选取目标函数时，用Pg[i] 替换式(6)中的Pi。

2.3 子问题三

3 最优解

3.1 子问题一的解

起初，本文尝试在固定t0的前提下用二分法来求Ta的最优值，接着固定Ta，再利用二分法来求t0的最优值，可求出近似值，代码执行效率虽不高，但能给出最优值的估计。后来利用边值问题打靶法的思路，在参考文献[12]中寻找优化代码，经过验证，方法奏效。关键python 代码如下：

x_cons_opt=optimize.minimize(f,[0.287,40.28],met hod='nelder-mead',

options={'maxiter':30,'xtol':0.01,'ftol':0.01,'disp': True},bounds=[bnd_ta,bnd_tj]).x

其中f 为目标函数，通过对ODE 初值问题(5)做数值积分，并计算目标函数值；接着给出两个参数的初值；所采用的优化方法是对非线性多元函数求局部极小值有效的Nelder-Mead 方法；options 中的内容很关键，它决定了程序何时停止，如果缺失options，程序运行可能不收敛，maxiter 乘以参数的个数给出了最大迭代次数，xtol 和ftol 控制精度，bounds 给出了解的搜索范围，比如T∊ [0.25,0.3]，t0∊[20,60]。数值积分采用了scipy 库函数，变步长四阶算法dopri5，选择步长为0.01，这保证了数值积分的精度。利用积分时长2000 ms，迭代运算53 次，第一小问的最优解为T= 0.28799396ms，t= 42.5590721ms，目标函数(6)对应的最优值约2.6312 MPa，图5 给出了对计算结果可靠的验证。

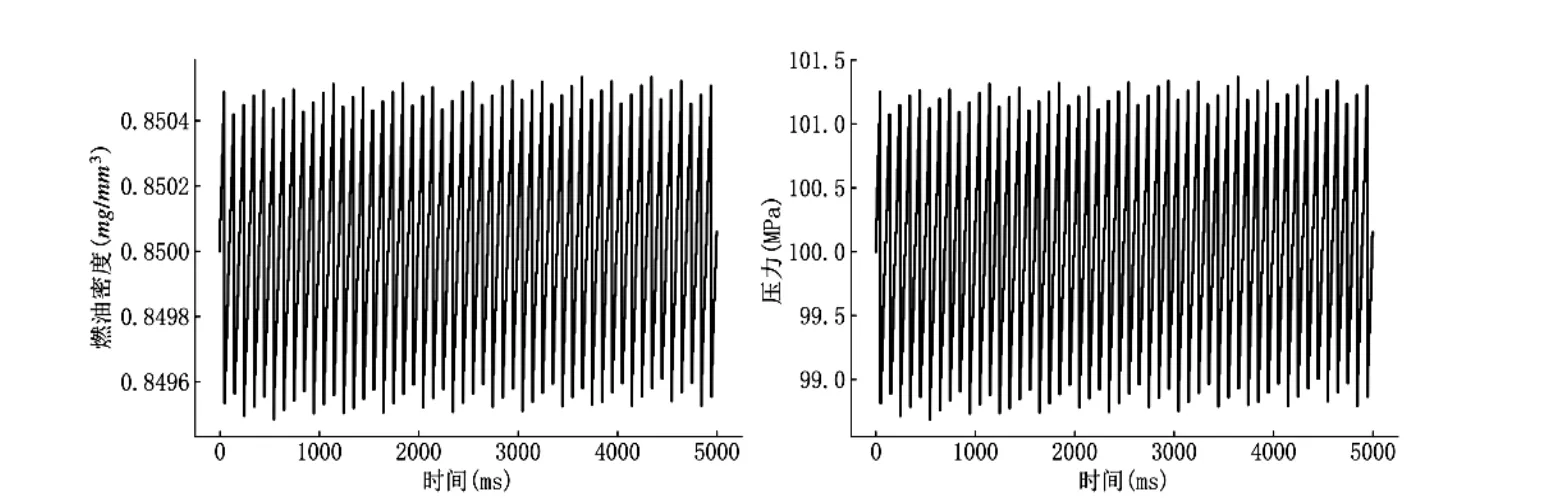
图5 初始压力为100 MPa 时选择Ta≈0.288 和t0≈42.56 使得高压油管内的压力尽量稳定在100 MPa

在计算初值的时候，也可以分析估计。在一个喷油周期内对喷油流量进行积分得44 毫升每百毫秒，进油流量15.35 毫升每毫秒，假设在100 毫秒内供喷平衡，得44 ≈ 15.35Ta×1 00/(10 +Ta)，而喷油次数为整数，可以估计出Ta∊(0.2866,0.2955)，在不考虑喷油时间延迟的情况下Ta取0.2951 较为合理，但在短期来说高压油管压力波动太大并不合乎题意。

在上述基础上，考虑压力稳定在150 MPa 的情形，式(5)的初值 (0.867920,150)。在分析方面，仍考虑100 毫秒内的供喷平衡方程44 ≈ 6.27T×1 00/(10 +T)，可以估计出在初始压力150 MPa、喷油不延时、长期工作条件情况下，单向阀最佳开启时长约0.7547 ms。在数值方面，先固定t0在40 附近，利用两步二分法，也可以得到较好的结果，但所得结果T≈0.7537 、t0≈ 39.673，对比使用优化算法所得结果Ta=0.753 84499、t0=45.7308504 还是稍逊一筹，后者为最优解。在前者作为初值、积分时长2000 ms、搜索范围为[0.7,0.8]× [30,50]时，迭代次数23 次，最优值约为3.1801，图6 可作为对最优解的验证。

图6 初始压力为150 MPa 时选择Ta≈0.754 和t0≈45.73 使得高压油管内的压力尽量稳定在150 MPa

考虑2 秒后实现将压力P 从100 增加到150，需要调整参数Ta和t0，使得式(7)的值最接近0，利用二分法可以给出较好的估计值T≈ 0.73125、t≈1004.88，目标函数值约7.2×10-3。在该参数值附近进行优化，更优的目标函数值约为1.32×10-4，最优解为Ta=0.730357993、t0=1003.04631。在2 秒后采用压力稳定在150 MPa 的参数，数值图像见图7。同理，考虑5 秒后P=150 情形，得最优解Ta=0.70251709，t0≈3.0×10-5≈0，目标函数值式(7)约5.03×10-4；考虑10 秒后P=150 情形，得最优解T≈ 0.700625，t0≈0，目标函数值式(7)约0.150。

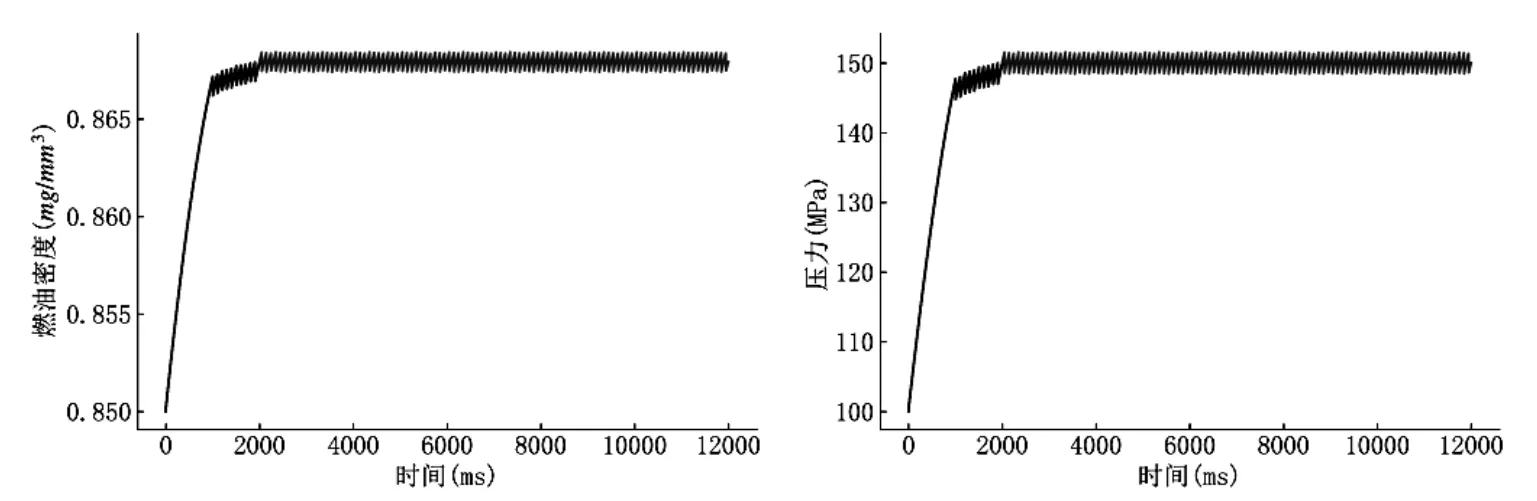
图7 两阶段控制策略使得高压油管内的压力在2 秒后尽量稳定在150 MPa

3.2 子问题二的解

问题二是个强非线性问题。可以积分求出喷油器在2.45 毫秒也就是一个喷油周期100 毫秒时间内的喷油量约38.7086，而在凸轮转动一周的时间内供油量约为67.706，供喷平衡方程近似为67.706×100ω /(2π )≈38.7086，得ω≈0.0359rad/ms，可以估计出凸轮角速度的数量级。数值计算得最优解是ω=0.0271478506、t0=109.194263，图8 给出了高压油管压力控制在(97.475,102.55)的效果。

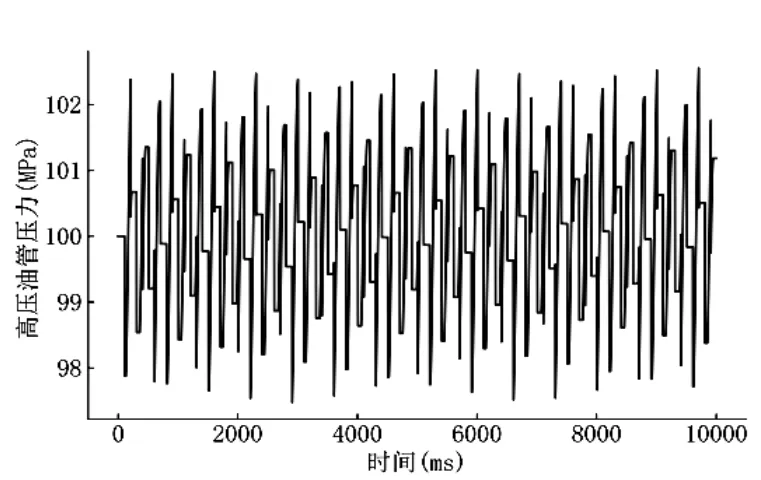
图8 通过凸轮转速和喷油时间延迟控制高压油管压力在100 MPa 附近效果

3.3 子问题三的解

假设甲乙两个喷油器喷油时间间隔t1，待优化的参数有三个，即凸轮转ω速、甲的喷射时间t0、乙的相对甲延迟喷射的时间t1。问题的难度相对子问题二增加了优化计算量。本文给出较优的解，即 ω=0.054 0722，t0=74.1114，t1=44.3691，目标函数值 (6) 的值约6.3647。高压油管内的压力波动见图9。

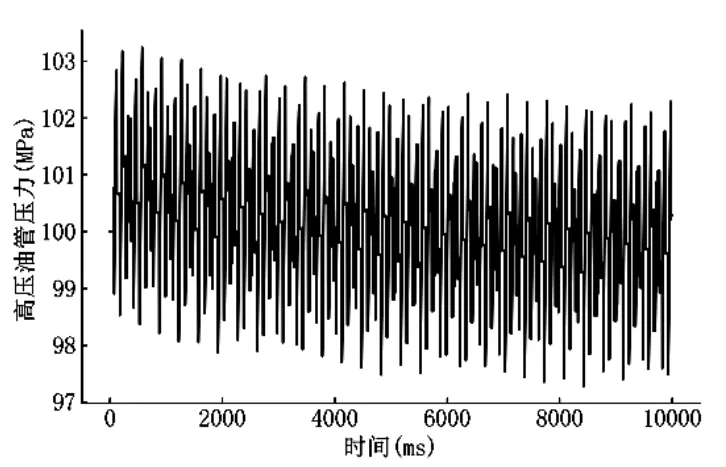
图9 双喷油嘴情况下进行参数控制使得高压油管内的压力在100 MPa 附近波动

考虑再增加一个减压单向阀。如果假设减压阀每工作t3时间便关闭时间t4，这样并不能求出最优解。

而假设减压阀在压力大于102 时打开，否则关闭，那么仍需优化3 个参数。经仿真，得到最优解5.67 ×10 ,75.1114, 45.25，目标函数值 (6) 的值约4.56，从图10 可以看出优化效果明显。

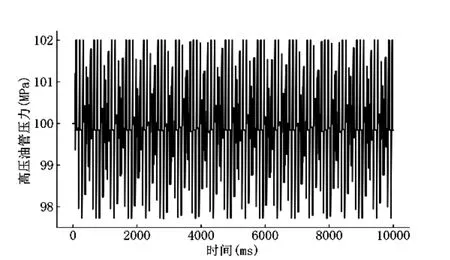
图10 有减压阀的双喷油嘴情况下高压油管压力控制效果

4 结论

本文以2019 年大学生数学建模题为问题来源，完整地给出了高压油管压力控制问题的微分方程模型，基于python 优化命令做数值计算，得到了关于燃油密度、针阀运动、凸轮曲线的精确拟合函数，最终给出了可靠的最优参数。由于喷油嘴外界的压力未知，本文采用标准大气压。所用方法和所得结论为燃油喷射系统精准控制提供有意义的参考。