基于局部方差的织物纹理周期测量方法

蔺曾上 潘如如 周 建

（江南大学，江苏无锡，214122）

纹理是一种普遍存在的视觉现象，能够直观反映物体表面同质现象的视觉特征。机织物由经纬纱按照一定规律交织而成，其织物图像表面呈现大量结构相似的局部纹理单元，即灰度变化在空间上呈现规律的重复性，具有明显周期特征。对于织物而言，对其表面纹理特征的准确描述是评价织物表面性能的基础，也是对织物纹理分类的前提。织物的周期作为其纹理特征的重要参数之一，对其周期进行研究可以为纺织领域的应用提供基础理论，如织物结构分类、缺陷检测和织物结构参数提取。

根据图像周期的不同定义，当前织物周期检测方法主要有傅里叶变换、自相关函数、灰度共生矩阵、距离匹配函数及Renyi′s 熵。傅里叶变换可以从全局的角度分析图像纹理［1-2］，将图像从空间域转化到频率域，然后在频率域进行周期检测，但该方法容易受到其他非主周期的干扰［3］。而自相关函数则是在空域中利用织物中纱线排列的规律性，计算图像纹理的相关系数来描述纹理信息［4］。与傅里叶变换相比，自相关函数的峰值会更为清晰，因此可以更容易地检测到织物的周期规律。灰度共生矩阵法则是根据织物的统计特性，提取所对应位移向量来实现周期的测量，虽然其正确率较高但计算量大［5-6］。OH G 等［7］在灰度共生矩阵的基础上，提出了距离匹配函数的周期测量方法，可以有效地改善计算效率，显著降低了计算成本。ASHA V 等［8］使用向前差分和累加DMF 进行计算，可以有效地检测到织物的纹理周期，但该方法容易受到噪声的影响。Renyi′s 熵方法是指在规定的窗口范围之内，构建一个Renyi′s 熵直方图，通过计算Renyi′s 的极小值，从而构建一个函数，计算图像的周期，但其容易受到纹理基元形状的要求，从而导致精度降低［9］。

针对上述不足，本研究提出一种新的基于局部方差的织物周期测量方法。通过对图像进行缩小，计算局部方差，得到局部方差曲线，从而实现织物图像的周期测量。与传统的自相关函数和距离匹配函数相比，该方法的准确性更高，误差更小，抗噪声干扰能力更强。

1 周期测量原理

1.1 局部方差

WOODCOCK C E 等［10］曾提出了一种可以用于探测遥感影像上地物尺度大小的方法——局部方差法（Local Variance），也被称为平均局部方差方法（Average Local Variance），是通过一个3×3 的窗口，在图像中从左至右，从上到下不断滑动，计算图像中各个窗口的标准差均值，即局部方差，最后通过观察图像中像素尺寸的变化，形成局部方差曲线图，来描述方差的变化。

采用如上所述的局部方差，本研究所提出的周期测量方法分为3 个步骤：首先，对原始图像进行图像缩小，以获取不同分辨率的图像；其次，采用一个m×n大小的移动窗口计算上述得到的每个分辨率图像的局部方差值；最后，将每个分辨率图像所对应的缩小倍数作为横坐标，并将所获取的局部方差值作为纵坐标，从而构建不同分辨率下的局部方差曲线图。

1.2 计算源图像的局部方差

为了直观描述局部方差计算过程，此处使用简单的理想周期图像作为实例，其过程如图1所示。

图1 移动窗口滑动过程

首先，在图像上创建一个1×2 的移动窗口（如图1 中红色部分），然后该窗口按着从左到右，从上到下的顺序进行滑动，直到遍历图像所有像素点，并记录下每次滑动窗口内的方差，记为S2。然后计算所有方差的平均值作为当前分辨率下的平均局部方差值，记为ALV，其公式如式（1）所示。

式中：Sp2为窗口滑动所对应的方差值；p为窗口数量，其值取决于滑动窗口尺寸和图像尺寸。

1.3 缩小图像

在得到源图像的局部方差值后，需要对源图像进行图像缩小。图像缩小的方法有很多，本研究利用简单缩小方法，即在图片中设置尺寸适当的窗口，将窗口中每个像素值的平均值作为缩小后的低分辨率图像的像素值，然后将窗口滑动，最终实现对整个图片的缩小处理。以此类推，通过设定不同窗口从而获得一系列缩小的图像。

通过对源图像缩小处理，获得一幅新的图像，并根据上述方法再次计算其局部方差值。如此反复，最终得到一系列ALV值，如图2 所示，用6 pixel×12 pixel 的织物图像作为源图像。

图2 图像缩小过程（仅在行方向上）

由图2 可以看出，图像的ALV值开始会随着图像缩小变大，但是当缩小倍数超过一定程度时，ALV值会变小，呈现出先增大后减小的趋势，当缩小倍数达到其周期值时［如图2（d）所示］，图像的ALV值为0。所以，规则图像的局部方差图会有一个谷值点，其对应的缩小倍数即为图像的周期值。

1.4 周期测量

在上一步中，会得到一系列不同缩小倍数的ALV值。之后以图像的缩小倍数为横坐标，以不同缩小倍数下得到的局部方差值为纵坐标，可以形成局部方差曲线图，该曲线图的最低点所对应的缩小倍数值即为所求周期值。所以，在求织物周期时，取最小的ALV值所对应的像素值为周期值。

但是，由于织物周期都较小，易受到其他噪声的干扰，从而导致曲线图的最低点所对应的缩小倍数往往大于其图像本身的周期值。为了减少噪声的干扰，获取图像中主要纹理基元的纹理周期，本研究依次检测每个谷值，将每个谷值所对应的缩小倍数值都视为其潜在周期值，之后计算每个谷值的ALV值与最小的ALV值之差，当其结果小于一定阈值时，则判定此谷值点所对应的像素值即为所求周期值，如式（2）所示。

式中：d为谷值点所对应的缩小倍数值；k为参数，通过对局部方差的试验发现，当参数k取0.04 时，其结果具有较好的自适应性。列方向上同理。

1.5 理想周期图像验证

为了验证上述方法的有效性，通过生成具有理想周期的三原组织（平纹、斜纹和缎纹）图像进行周期测量验证测试，理想斜纹布图像如图3所示。

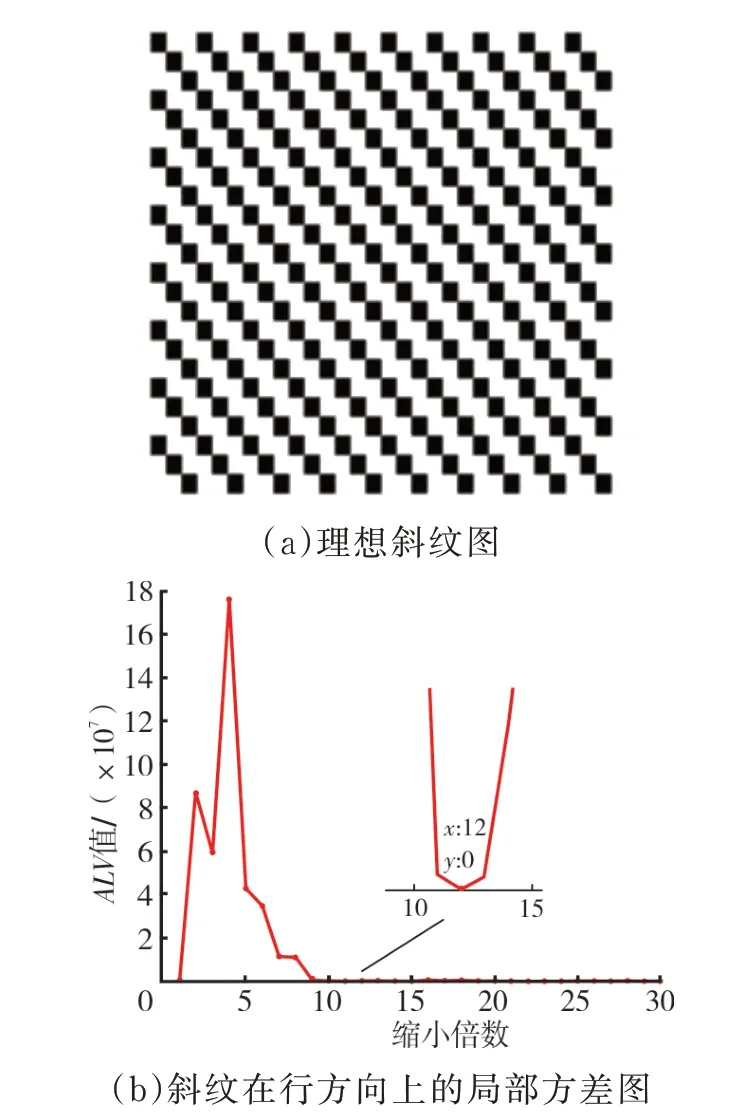
图3 理想斜纹布图像

表1 是3 种纹理图像的实际周期与局部方差计算周期的比较结果，其中，Tr表示行方向上周期，Tc表示列方向上周期。由于是理想周期纹理，实际的周期和本研究方法计算得到的周期是完全一致，表明文中上述所提方法合理可行。

表1 理想织物纹理的周期

2 试验结果与讨论

2.1 Brodatz 纹理周期提取试验

为了检验本研究方法检测纹理周期的有效性和准确性，首先对Brodatz 数据库中结构性纹理图像周期进行测试。Brodatz 纹理库是最经典的自然纹理数据库，部分纹理如图4 所示。

图4 Brodatz 纹理库

考虑到数据库中样本的纹理周期都较小，所以设置缩小倍数为2～50，从而提高测量的准确性与运行速度，实际应用时也可根据纹理周期的大概范围来进行调整。部分纹理周期测量结果如表2 所示。

表2 Brodatz 图像周期表

对比表2 可以发现，使用本研究算法计算的行方向和列方向的周期相对误差都较小。由于D6、D20、D21 和D102 这4 幅图像具有很强的规律性，因此它们的误差很小，即使图像中存在局部的形变，使用本研究算法进行研究也不会影响计算的准确性。由于D52 在行方向上存在明显的形变，因此它们的行周期误差明显高于列周期误差。而D53 则在垂直方向上表现出明显的形变，因此它们的列周期误差明显高于行周期误差。尽管D34 表现出较大的形变，导致测量误差较大，但仍然能够相对准确地测量出纹理周期，说明本研究方法具备了一定抗干扰性。通过使用Brodatz纹理库中的图像，可以发现本研究方法能够有效抵御干扰，相对误差仅为2.6%。

2.2 织物纹理周期提取试验

为了进一步探究本研究方法在织物纹理中的应用，首先对织物纹理进行分类。在本试验中，将织物纹理分为平纹、斜纹、缎纹、素色小提花和图案共5 类，选择512 pixel×512 pixel 的织物样本，并设置缩小倍数为2～30，个别织物的缩小倍数可适当扩大。其中，P1～P6 为平纹布，T1～T6 为斜纹布，S1～S6 为缎纹布，D1～D6 为素色小提花织物，Z1～Z6 为图案织物。此外，为了更好地验证本研究方法的有效性，还将其与累加DMF 方法和自相关函数法进行了对比，相关试验结果如表3 所示。

表3 织物周期提取结果对比

对表3 中试验结果分析可知，本研究方法检测织物周期更接近实际的织物周期，而累加DMF和自相关函数方法容易受到其他纹理周期的干扰，其稳定性与准确率不如本研究方法。究其原因，由于织物经纬纱线粗细不一致、在经纬方向上受力不均，并且表面毛羽与纱线的摩擦产生起毛起球现象等因素，极易造成纹理的形变，使得织物的纹理呈现出多样性，而通过本研究方法，可以从微观的角度研究纹理的周期性，有效减少由于织物图像的经纬变化而导致的周期性偏差。部分试验结果如图5 所示。

图5 试验结果（局部放大图）

2.3 抗椒盐噪声试验

为了进一步验证本研究方法的抗噪声性能，手动为图片增加了椒盐噪声，同时与累加DMF方法进行性能对比，如图6、图7 所示。

图6 试验图像

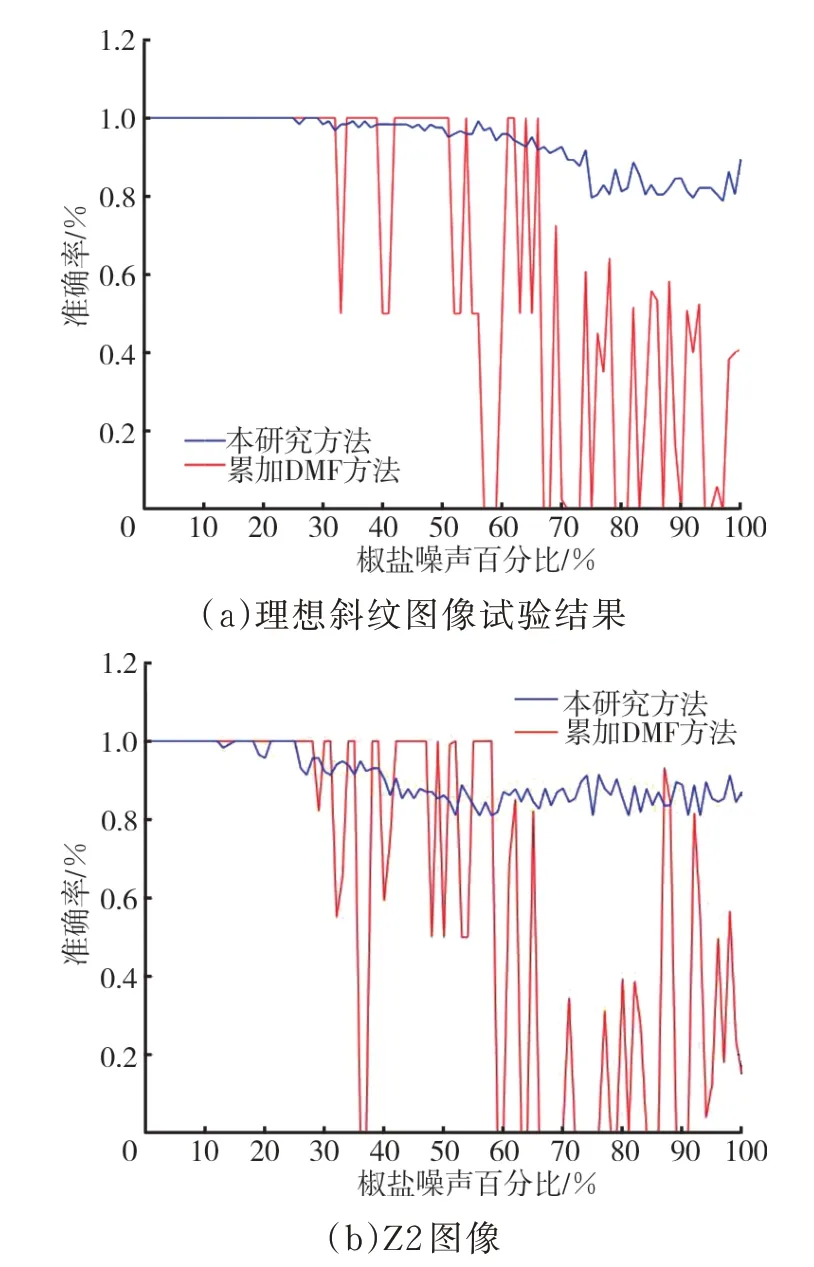
图7 抗噪声试验结果

椒盐噪声又叫冲击噪声（或者脉冲噪声）。在图像中表现为离散分布的纯白色或者黑色像素点。本研究使用纹理基元大小为60 pixel×60 pixel，540 pixel×540 pixel 的理想斜纹布与图像Z2 作为原始图像（如图6 所示），依照噪声占整个像素总数的百分比，增加椒盐噪声从1%依次到100%，共计使用200 幅图像进行验证，试验结果如图7 所示。由图7 可见，本研究方法的试验结果要优于累加DMF 方法。累加DMF 方法会随着噪声密度的增加愈发不稳定，而本研究方法的稳定性则远远好于DMF 方法，在强噪声的干扰下，依旧能保持较高的准确率（80%以上）。

3 结语

本研究通过局部方差，实现了对织物纹理的周期测量。通过计算织物图像的局部方差，可以从微观的角度研究织物纹理的周期性，实现织物周期的准确测量。试验证明，本研究提出的方法能够准确地测量织物纹理周期，其相对误差仅为2.6%，相比传统的累加DMF 方法和自相关函数法，其准确性更高，抗噪声性能更好，更适用于织物纹理周期的测量。