基于GA-BP 的多目标PEDOT∶PSS 导电非织造布性能优化

张天芸 王芃生 吴娇娇

（1.兰州理工大学，甘肃兰州，730500；2.浙江昶丰新材料有限公司，浙江丽水，323010）

导电非织造布是指在纺织非织造布中添加导电材料，使其具有一定的导电性能和机械性能，并最大限度地保留原非织造布的纺织性能［1］。其中，聚（3，4-乙撑二氧噻吩）∶聚（苯乙烯磺酸）（PEDOT∶PSS）一般采用溶液混合法或电化学合成法制备。在制备过程中，3，4-乙烯二氧噻吩（EDOT）和聚（苯乙烯磺酸）（PSS）的摩尔比例、溶剂的种类和浓度等因素均会影响PEDOT∶PSS导电聚合物的性能。

使用浸涂法制备PEDOT∶PSS 导电非织造布的过程中，综合性能优越的导电材料是确保导电非织造布具备优良导电性能和机械性能的关键［2］。为此，针对其材料配比与综合性能优化问题开展了大量研究。李蛟［3］通过掺杂、热处理以及外加电场等实现了PEDOT∶PSS 导电性能优化；陈志刚团队［4］采用甲酰胺、浓硫酸和硼氢化钠溶液，选择性去除薄膜中多余的PSS 掺杂物，有效提高了其导电性能。 这些方法在优化PEDOT∶PSS 导电性能方面取得了一定的效果，但仍存在一些局限。例如：进行掺杂处理后，PEDOT∶PSS 导电非织造布的弹性变差，脆性增大，影响了导电非织造布包括透气性在内的众多纺织性能，因此有必要针对PEDOT∶PSS 导电非织造布的性能进行优化［5］。

本研究以浸涂法制备导电非织造布为基础，重点考察了EDOT 与PSS 摩尔比例、过硫酸铵浓度、硫酸铁浓度、HCl 质量分数对导电非织造布性能的影响。并依据试验所测数据，构建制备PEDOT∶PSS 导电材料配比和导电非织造布性能之间非线性关系的BP 神经网络模型。此外，为了提高 BP 神经网络的预测精度，通过将遗传算法应用于优化神经网络的权值和阈值来构建精度更高的GA-BP 神经网络。最后，基于该模型构造适应度函数进行多目标寻优得到最佳配比，制得综合性能优良的PEDOT∶PSS 导电非织造布。

1 PEDOT∶PSS 导电非织造布的制备

1.1 碱减量处理

配置不同浓度的NaOH 水溶液，加入基布（涤/棉 65/35 非织造布，单位面积质量为134 g/m2）后充分搅拌再洗涤烘干。从图1 可以看出，未经碱减量处理的涤/棉 65/35 非织造布的纤维表面存在毛羽、杂质等微小结构，经碱减量处理后，涤/棉65/35 非织造布与NaOH 水溶液发生了水解反应，使纤维表层非晶区大分子链端酯基发生水解，并逐渐向内发展，有效去除纤维表面杂质并在纤维表面产生刻痕，提高对导电液的黏附能力。

图1 碱减量处理前后纤维微观形貌

设计了5 组不同浓度NaOH 水溶液碱减量处理梯度试验。试验条件：裁剪5 组5 cm×5 cm的涤棉非织造布，分别进行不同浓度碱减量处理，烘干后测量其质量变化并计算出失重率；随后将其浸入相同配比的PEDOT∶PSS 导电聚合物溶液中进行涂敷处理，测量质量变化并计算出附着率。

图2 碱减量处理后非织造布失重率及附着率变化图

结合图1 涤棉非织造布碱减量处理前后微观形态变化可得：当NaOH 水溶液浓度在0 mol/L～1.0 mol/L 区间，非织造布失重率和附着率的增长率较大；在1.0 mol/L～2.0 mol/L 区间，失重率和附着率基本呈现稳定状态。过高浓度碱减量处理会影响非织造布机械性能，综合考虑NaOH水溶液浓度为1.0 mol/L 时进行碱减量处理效果最佳，在保证织物形态更为完整的基础上，可以有效提高涤棉非织造布的导电聚合物附着率。

1.2 浸涂法制备PEDOT∶PSS 导电非织造布

准备20 组5 cm×5 cm 的涤棉非织造布并进行碱减量处理。分别以EDOT 与PSS 摩尔比例（ω1），过硫酸铵浓度（ω2），硫酸铁浓度（ω3）和盐酸质量分数（ω4）为变量，设置5 组梯度试验。以过硫酸铵和硫酸铁作为氧化剂及催化剂，将EDOT与PSS 在酸性环境下聚合为PEDOT∶PSS 导电材料［6］，具体反应过程如图3 所示。最后，采用涂敷工艺将所制得PEDOT∶PSS 导电材料均匀涂敷于碱减量处理后的非织造布表面，从而制备出导电性能优良的PEDOT∶PSS 导电非织造布。

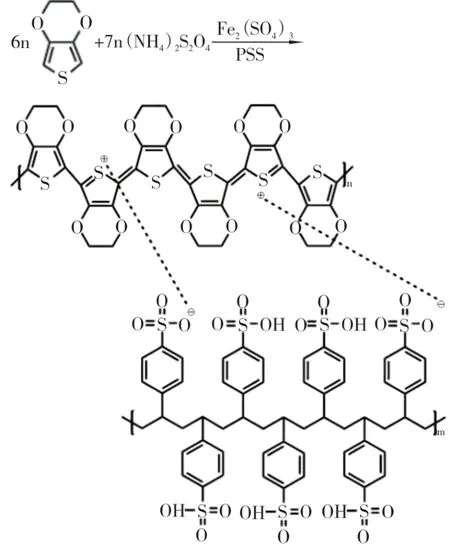
图3 PEDOT∶PSS 反应过程

1.3 导电非织造布性能表征

1.3.1导电性能表征

搭建一套由万用表、导线、夹具和4 块铜板组成的测试系统。利用电阻率和电导率计算公式，根据所测数据得到导电非织造布样品的电导率和电阻率等指标［7］。导电非织造布电阻率计算公式如下。

式中：ρ为电阻率（Ω·m）；R为电阻值（Ω）；A为电阻横截面积（m2）；L为电阻长度（m）。

由于导电非织造布电导率为电阻率的倒数，因此计算公式如下。

式中：σ为电导率（S/m）。由导电非织造布电阻率及电导率计算公式，即可得不同条件下PEDOT∶PSS 导电非织造布的导电性能。

1.3.2力学性能表征

本研究以拉伸断裂强度作为机械性能的评价指标。按照GB/T 3923.1—2013《纺织品 织物拉伸性能 第1 部分：断裂强力和断裂伸长率的测定（条样法）》中的测试方法，采用YG（B）026H-250型电子织物强力机测试PEDOT∶PSS 导电非织造布的拉伸断裂强力，并计算出织物拉伸断裂强度，所得数据如图4 所示。

图4 涤棉非织造布力学性能数据折线图

由图4 可以看出：断裂伸长率呈现先减后增的趋势，拉伸断裂强度呈现下降趋势。随NaOH水溶液浓度的增加，涤棉非织造布断裂伸长率由79%降为65%，拉伸断裂强度由8.72 MPa 降为3.90 MPa。主要原因是，在碱减量处理过程中，NaOH 水溶液使纤维的表面和内部结构受损，破坏了纤维的结晶结构，降低纤维的结晶度和有序性，从而降低了纤维的拉伸断裂强度和断裂伸长率。但随着NaOH 水溶液浓度的提高，纤维表层非晶区大分子链端酯基的水解反应加剧，有效去除了纤维表面杂质并使纤维细度和柔软度增加，导致涤棉非织造布的断裂伸长率小幅度增加。

2 BP 神经网络模型构建

2.1 样本数据处理

BP 神经网络的样本数据是构建模型的关键。表1 为PEDOT∶PSS 导电材料配比学习样本数据，表2 为归一化后的样本数据。归一化可以使样本数据具有统一的尺度，避免了各影响因素之间数值差异过大的问题。选取1.0 mol/L NaOH 水溶液碱减量处理后的涤棉非织造布为基材，并根据表1 中PEDOT∶PSS 导电聚合物配比制备导电材料，最后将导电聚合物均匀涂敷于基布上，室温风干。其中，影响导电非织造布性能的PEDOT∶PSS 导电材料配比参数有EDOT 与PSS 摩尔比例（ω1）、过硫酸铵浓度（ω2）、硫酸铁浓度（ω3）和盐酸质量分数（ω4）。随后，将1 组～10组用作神经网络训练集，11 组～20 组用作测试集，隐含层采用Sigmoid 函数，输出层采用Purelin函数。由于Sigmoid 函数值域范围是[-1，1]或[0，1]，因此为了避免产生较大误差，需要对数据进行归一化处理［9］。

表1 PEDOT∶PSS 导电材料配比学习样本数据

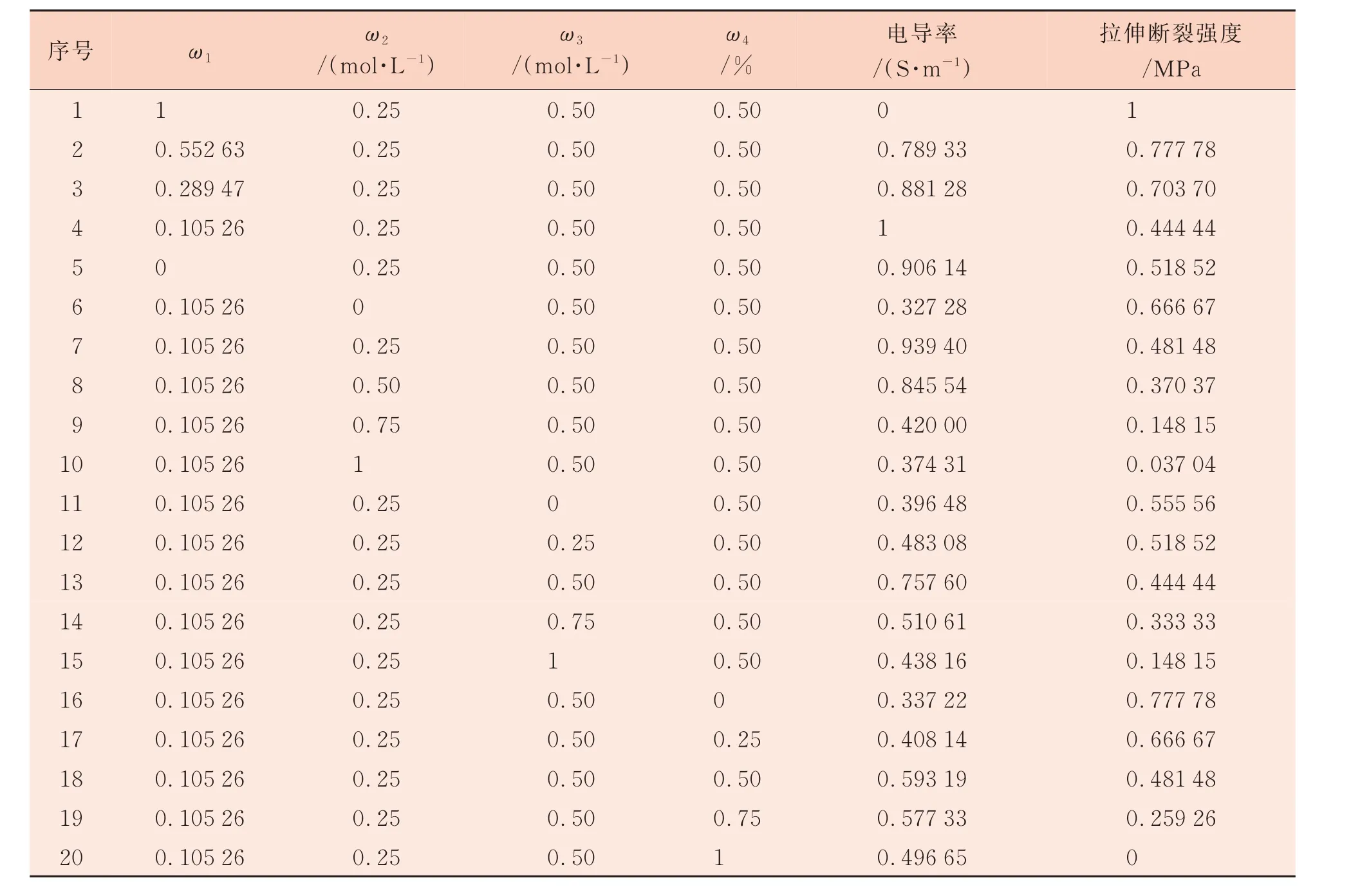
表2 归一化处理后PEDOT∶PSS 导电材料配比学习样本数据

2.2 BP 神经网络结构设计及优化

2.2.1BP 神经网络参数设计

BP 神经网络模型主要由输入层、隐含层和输出层组成。在该问题求解过程中，神经网络的输入参数为PEDOT∶PSS 导电材料配比参数ω1、ω2、ω3和ω4，输出参数为所制备导电非织造布的电导率及拉伸断裂强度，输入层神经元个数为4，输出层神经元个数为2，学习速率为0.05，训练集迭代次数设为1 000。此外，隐含层神经元数利用公式（3）估算出范围，进而选择误差最小的隐含层神经元个数［10］。

式中：n1为隐含层神经元个数；n为输入层神经元个数；m为输出层神经元个数；a为[1，10]范围内的常数。

为确保模型的准确性，对不同隐含层神经元个数的神经网络模型进行误差分析，分别训练10次后取平均误差为最后误差评价指标。

式中：MAE为样本误差值；N为样本个数；y′i和yi分别表示预测值和期望值。

所得误差分析数据如表3 所示，当隐含层神经元个数为11 时，神经网络误差最小。

表3 不同神经元数量的神经网络误差对比

2.2.2基于GA-BP 神经网络优化

遗传算法（GA）是一种模拟自然选择和遗传机制的优化算法，它通过模拟进化过程中的选择、交叉和变异等操作，基于反向传播算法来调整网络中的权重和偏置，以最小化损失函数，最终寻求最优解［11］。

GA-BP 神经网络构建流程［12］如图5 所示。

图5 GA-BP 神经网络构建流程图

由于遗传算法在迭代过程中不受外界影响，因此适应度函数的选取对收敛速度和寻找最优解起到了决定性的作用［13］。因此，样本模型适应度函数如下。

式中：F为样本模型适应度；Y1为实际输出值；Y2为期望输出值。

由于遗传算子在GA-BP 神经网络用于模拟自然界中的遗传机制［14］。因此，本研究中遗传算子采用随机遍历抽样；交叉算子采用单点交叉算子，交叉概率为0.5，种群大小为2 000，最大遗传代数为102 代。

随机选取表2 中10 组数据为训练集代入BP神经网络和GA-BP 神经网络进行训练。并选取表2 中11 组～20 组数据比较两者预测精度，结果如图6 所示。

图6 测试集预测结果对比图

经研究分析，相比于对照组实际所测电导率，GA-BP 神经网络的平均误差约为0.057 2，而BP神经网络的平均误差为0.091 5，其结果见表4。因此可以得出结论：GA-BP 神经网络的整体预测效果优于BP 神经网络，更适合用于PEDOT∶PSS 最优配比问题。

表4 BP 神经网络与GA-BP 神经网络对比

2.3 基于GA-BP 的多目标优化PEDOT∶PSS 导电材料配比

在该问题的求解中，通过GA-BP 神经网络模型进行仿真或预测，定义了神经网络结构和参数设置，其目标函数如下。

适应度函数直接影响遗传算法是否收敛，由于MATLAB 遗传算法默认求解最小值问题［15］。因此，适应度函数如下。

通过遗传算法多目标全局寻优，迭代102 次后得到最优配比组合为：EDOT 与PSS 摩尔比例0.334 5、过硫酸铵浓度0.029 7 mol/L、硫酸铁浓度0.048 7 mol/L、盐酸质量分数6.963 0%，此时PEDOT∶PSS 导电非织造布电导率为6.713 S/m，非织造布拉伸断裂强度为4.581 MPa。

3 导电非织造布电导率稳定性分析

作为一种柔性导电材料，PEDOT∶PSS 导电非织造布的电导率稳定性至关重要。PEDOT∶PSS 导电非织造布的电导率稳定性需要考虑到日常使用过程中水洗和摩擦的影响，故分别设置5组试验来探究PEDOT∶PSS 导电非织造布在摩擦和水洗过程中电导率的变化。根据GA-BP 神经网络所得最佳理论配比，将所得配比进行简化，即EDOT 与PSS 摩尔比例1∶3、过硫酸铵浓度0.03 mol/L、硫酸铁浓度0.05 mol/L、盐酸质量分数7%。在该条件下，制备出10 组PEDOT∶PSS 导电非织造布分别进行摩擦和水洗测试。

3.1 摩擦影响

PEDOT∶PSS 导电非织造布经摩擦后会对其电学性能产生影响［16］。在马丁代尔耐磨试验仪上，对制备的导电非织造布进行不同程度的摩擦，探究摩擦时间（0 min，5 min，10 min，15 min，20 min）对PEDOT∶PSS 导电非织造布的电导率影响，结果显示经过不同摩擦时间处理后织物的电导率分别为6.329 S/m，5.917 S/m，5.618 S/m，5.464 S/m，5.348 S/m。PEDOT∶PSS 导电非织造布表面含有大量的PEDOT∶PSS 导电颗粒，经5 min 摩擦后，导电非织造布表面结合力变差，造成PEDOT∶PSS 导电颗粒部分发生脱落，降低了导电非织造布导电网络的完整性，导致其电导率下降。电导率由6.329 S/m（0 min）降为5.917 S/m（5 min）。但随着摩擦时间的继续增加，导电非织造布电导率的下降幅度逐渐减缓，经20 min 摩擦后，其电导率仅降为5.348 S/m，说明制备的导电织物具有较好的耐摩擦使用性。

3.2 水洗影响

对PEDOT∶PSS 导电非织造布进行不同时间（0 min，15 min，30 min，45 min，60 min）的水洗，水洗后织物的电导率分别为6.536 S/m，5.917 S/m，5.682 S/m，5.525 S/m，5.435 S/m。PEDOT∶PSS 导电非织造布中的导电颗粒会在洗涤过程中发生轻微溶解，破坏了导电网络完整性，导致其电导率下降，电导率由6.536 S/m（0 min）降为5.917 S/m（15 min）。随洗涤时间增长，PEDOT∶PSS 导电非织造布电导率的下降幅度逐渐减缓，经60 min 洗涤后，其电导率降至5.435 S/m，表明制备的导电非织造布具有较好的耐水洗性。

4 结论

（1）基于GA-BP 的多目标全局寻优，制备导电非织造布的最佳配比组合为EDOT 与PSS 摩尔比例0.334 5、过硫酸铵浓度0.029 7 mol/L、硫酸铁浓度0.048 7 mol/L、盐酸质量分数6.963 0 %，此时PEDOT∶PSS 导电非织造布电导率为6.713 S/m，非织造布拉伸断裂强度为4.581 MPa。

（2）根据模型构建，通过试验得到导电非织造布，将该配比优化为：EDOT 与PSS 摩尔比例1∶3、过硫酸铵浓度0.03 mol/L、硫酸铁浓度0.05 mol/L、盐酸质量分数7%。在该条件下，导电非织造布经60 min 水洗后电导率由6.536 S/m降至5.435 S/m，经过20 min 摩擦后织物电导率由6.329 S/m 降至5.348 S/m 并趋于稳定，表明该导电织物具有较好的使用稳定性。