Commuting Linear Maps on a Kind of Heisenberg-Virasoro Lie Algebra

XU Yue, YANG Ningjing, GAO Shoulan

(School of Science, Huzhou University, Huzhou 313000, China)

Abstract： Using the properties of commuting linear maps, we calculate the commuting linear maps of the Heisenberg-Virasoro Lie algebra of rank two, which is helpful to determine the centroid of the Lie algebra.

Keywords： Heisenberg-Virasoro Lie algebra of rank two; commuting linear map; center

0 Introduction

The structures and representations of the Heisenberg-Virasoro Lie algebra and its generalizations have been widely studied, such as [1]～[7]. The Heisenberg-Virasoro Lie algebra of rank one is the Lie algebra of differential operators of order at most one[1], which is generalized to the case of rank two in [8]. Some structure properties of the Heisenberg-Virasoro Lie algebra of rank two have been calculated in [8], including central extensions, derivations and the automorphism group. In [9],-graded Harish-Chandra modules of the Heisenberg-Virasoro Lie algebra of rank two was classified. Now there are still many questions unknown about this Lie algebra.

Linear maps on Lie algebras are important part of the structure theory of Lie algebras, such as derivation, endomorphism and automorphism and so on. Commuting linear maps on Lie algebra is a special kind of linear maps, and it is an indispensable part of the structure theory of Lie algebras. In this paper, we mainly study the commuting linear maps on the Heisenberg-Virasoro Lie algebra of rank two.

Throughout this paper, we denote by,*,,*and theset of integers, non-zero integers, rational numbers, non-zero rational numbers and complex numbers, respectively. All the vector spaces are assumed over the complex field.

1 Preliminary

LetG={α=(α1,α2)|α1,α2∈,α≠(0,0)} and*={0,-1}.Set

η=(1,0),ε=(0,1).

Forα=(α1,α2),β=(β1,β2)∈G, denote by

Obviously, det(β,α)=0 if and only if the set{α,β} is linear dependent, and det(β,α)≠0 if and only if the set{α,β} is linear independent.

For anyα∈G, set

Z(α)={qα∈G|q∈*}.

Then, forα,β∈G, we have det(β,α)=0 if and only ifβ∈Z(α), and det(β,α)≠0 if and only ifβ∉Z(α).

Definition 1[8-9]The Heisenberg-Virasoro Lie algebra of rank two, denoted by g, has a basis

{tα,Eα,Ki|α∈G,i=1,2,3,4}

with the following brackets：

[tα,tβ]=0, [Ki,g]=0,i=1,2,3,4,

[tα,Eβ]=det(β,α)tα+β+δα+β,0(α1K1+α2K2),

[Eα,Eβ]=det(β,α)Eα+β+δα+β,0(α1K3+α2K4)

for allα,β∈G.

Obviously, the center of the Heisenberg-Virasoro Lie algebra of rank twoC(g)=CK1⊕CK2⊕CK3⊕CK4. According to Definition 1, when the set{α,β} is linear dependent andβ≠-α, we have

[tα,tβ]=[tα,Eβ]=[Eα,Eβ]=0.

2 Commuting linear maps on the Lie algebra g

In this section, we determine commuting linear maps on the Heisenberg-Virasoro Lie algebra of rank two g.

Definition 2[10]LetLbe a Lie algebra over the field F. A linear mapf：L→Lis called a commuting linear map of the Lie algebraLif

[x,f(x)]=0

for allx∈L.

For any commuting linear mapfof a Lie algebraL, it is easy to see that

f(Ki)∈C(g),i=1,2,3,4;

[f(x),y]=[x,f(y)], ∀x,y∈L.

for allα∈G.

ProofLetfbe any commuting linear map on g. For anyα∈G, assume

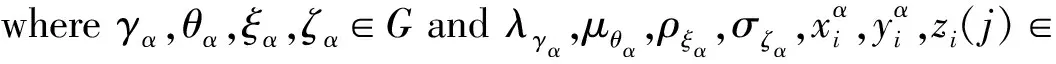
Since [tα,f(tα)]=0, we have

0=∑λγα[tα,tγα]+∑μθα[tα,Eθα]=
∑μθα[det(θα,α)tα+θα+δα+θα,0(α1K1+α2K2)]=
∑μθαdet(θα,α)tα+θα+μ-α(α1K1+α2K2),

which forces

det(θα,α)μθα=0,

(1)

α1μ-α=0,α2μ-α=0.

(2)

Sinceα=(α1,α2)≠(0,0), by(2), we have

μ-α=0.

Using(1), it is easy to seeμθα=0 if det(θα,α)≠0, that is,μθα=0 ifθα∉Z(α).

Hence, we can write

(3)

Since [Eα,f(Eα)]=0, we have

0=∑ρξα[Eα,tξα]+∑σζα[Eα,Eζα]=
-∑ρξα[det(α,ξα)tα+ξα-δα+ξα,0(α1K1+α2K2)]+
∑σζα[det(ζα,α)Eα+ζα+δα+ζα,0(α1K3+α2K4)]=
-∑ρξαdet(α,ξα)tα+ξα+ρ-α(α1K1+α2K2)+
∑σζαdet(ζα,α)Eα+ζα+σ-α(α1K3+α2K4).

Then we have

det(α,ξα)ρξα=0,

(4)

α1ρ-α=0,α2ρ-α=0,

(5)

det(ζα,α)σζα=0,

(6)

α1σ-α=0,α2σ-α=0.

(7)

Sinceα=(α1,α2)≠(0,0), by (5) and (7), we have

ρ-α=0,σ-α=0.

By (4), we haveρξα=0 ifξα∉Z(α). By (6), we haveσζα=0 ifζα∉Z(α).Then we can write

(8)

Using [f(tα),Eα]=[tα,f(Eα)], by (3) and (8), since

[f(tα),Eα]=∑λγα[det(α,γα)tα+γα-δα+γα,0(α1K1+α2K2)]+

∑λγαdet(α,γα)tα+γα-λ-α(α1K1+α2K2),

we have

∑λγαdet(α,γα)tα+γα-λ-α(α1K1+α2K2)=0.

Obviously,λ-α=0, andλγα=0 ifγα∉Z(α). Then (3) becomes

(9)

Using [f(tα),tβ]=[tα,f(tβ)], by (9), since

we get

(10)

Takeβ∉Z(α) in (10), then the set{α,β} is linear independent. So det(qα,β)≠0,β+qα≠0,det(qβ,α)≠0 andα+qβ≠0 for anyq∈*, which forces (10)becomes

(11)

Then

μqαdet(qα,β)tβ+qα=0,q≠0,±1.

It is easy to see that

μqα=0,q≠0,±1.

Hence (9) becomes

(12)

It follows from (11) that

det(α,β)(μβ-μα)tβ+α=0.

If the set{α,β} is linear independent, then det(α,β)≠0 and

μβ=μα.

Thenμα=μεforα≠lε, andμlε=μη=με, wherel∈*. So

μα=με, ∀α∈G.

Hence (12) becomes

(13)

Using [f(tα),Eβ]=[tα,f(Eβ)], by (8) and (13), since

we have

με[det(β,α)Eα+β+δα+β,0(α1K3+α2K4)]=

(14)

Takingβ=-αin (14), we getμε(α1K3+α2K4)=0.Hence

με=0

(15)

and (14) becomes

(16)

Take β∉Z(α) in (16), then

which forces that

λpαdet(β,pα)=0,σpβdet(pβ,α)=0,p≠0,±1;

λαdet(β,α)=σβdet(β,α).

It is easy to see that

(17)

Using (17), we getλα=σεforα≠lε, andλlε=ση=σε, wherel∈*. So

λα=σε, ∀α∈G.

Similarly,σβ=λε=σεforβ≠lε, andσlε=λη=σε, wherel∈*. So

σβ=σε, ∀β∈G.

Therefore,

λα=σα=σε, ∀α∈G.

Setσε=a. Then (13) and (8) become

(18)

(19)

via (15) and (17).

By (19), we can obtion

Since [f(Eα),Eβ]=[Eα,f(Eβ)], we get

(20)

Takeβ∉Z(α) in (20), then

which forces that

ρsαdet(β,sα)=0,s≠0,±1;

ραdet(β,α)=ρβdet(β,α),s=1.

It is easy to see that

(21)

Thenρα=ρεforα≠lε, andρlε=ρη=ρε, wherel∈*. So

ρα=ρε, ∀α∈G.

(22)

Setb=ρε. According to (21) and (22),

(23)

Therefore, the theorem holds via (18) and (23).