溶滞网络缓冲区占用率预测模型设计

刘 博,康 旖,陈禹旭,梁子键,李晓璐

(南方电网数字电网集团有限公司,广东 广州 510700)

0 引言

多组件融合技术可以按照相似性聚合标准将具有相关性映射关系的数据样本关联在一起,以保证互联网络的布局合理性、避免信息样本出现过度累积的情况。

溶滞网络是包含路由协议的存储与转发的网络。由于其具有高延迟的特性,故数据样本的连接在缓冲区域内会表现出间接性。这也是导致网络缓冲区占用率过高的主要原因。文献[1]基于多层前馈神经网络的预测模型,借助神经性节点过滤溶滞网络中的非必要传输数据,并利用多层前馈神经网络组件,将这些信息样本整合成多个数据包存储结构。文献[2]基于循环神经网络的预测模型,主要通过复杂化数据样本传输路径的方式,缓解溶滞网络的数据拥堵情况。由于网络环境内包含多台数据库主机,所以未被完全消耗的信息样本可被这些元件设备直接存储。文献[3]提出长短时记忆网络预测模型,旨在去除溶滞网络中不具备自主传输能力的数据样本,并通过多次处理过程使得网络体系的信息存储压力得到缓解。然而,随着网络运行时间的延长,上述3种方法的信道平均占用率并不能保持在既定数值标准之内,占用率相对较高。

为此,本文构建基于多组件融合的溶滞网络缓冲区占用率预测模型。首先,本文在多组件框架的基础上,融合溶滞网络缓冲区内的数据样本,并配置可移植的任务。然后,本文基于获取的任务,根据溶滞缺失值计算结果,设计基于决策树的溶滞网络缓冲区占用率预测模型。最后,本文通过试验验证了该模型具有较好的预测效果。该模型为解决溶滞网络中数据滞留引起的缓冲区内存不足的问题提供了参考。

1 溶滞网络缓冲区内的数据样本处理

溶滞网络缓冲区内的数据样本处理需要在多组件框架的基础上,推导数据样本融合条件,并联合可应用信息参量,确定可移植任务的配置情况。

1.1 多组件框架

在溶滞网络中,多组件框架同时管控Linux数据库、网络服务层、顶层缓冲单元、Java组件等多个预测结构。溶滞网络的多组件预测框架如图1所示。

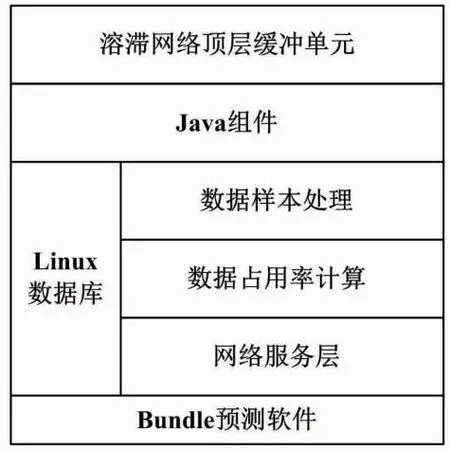
图1 溶滞网络的多组件预测框架

Bundle预测软件可以直接提取溶滞网络缓冲区内的拥塞数据参量,并可以借助传输信道将这些信息样本反馈至网络服务层结构中。当前情况下,若Linux数据库中已存储样本满足信息参量的多组件融合条件,Java组件就可以在处理数据样本的同时,对数据占用率进行计算[4-5]。

本文设α为网络溶滞系数的最小取值结果、ε为最大取值结果、β为多组件框架内的数据样本辨别系数、Vα为基于α的溶滞网络缓冲特征值;Vε为基于ε的溶滞网络缓冲特征值。在设置多组件框架时,α∈(1,e)、ε∈(1,e)的赋值条件同时成立。本文联立上述物理量,将多组件框架对于数据占用率的计算式定义为:

(1)

Java组件[6]对于溶滞网络缓冲区内拥塞数据参量的处理能力,决定了多组件框架的运行能力。为避免顶层缓冲单元中出现信息参量过存储情况,本文在设置多组件框架时,要求数据占用率计算结果不得超过溶滞网络缓冲区组织对数据信息样本最大存储能力的50%。

1.2 数据样本融合条件

数据样本融合条件决定了溶滞网络缓冲区的当前占用率水平是否具备继续存储数据信息参量的能力。当选取的数值样本趋近于1时,表明溶滞网络缓冲区占用率水平较高,基本不具备继续存储数据信息参量的能力;当选取的数值样本趋近于0时,表明溶滞网络缓冲区占用率水平较低,可以继续存储数据信息。本文以多组件框架作为必要预测结构,根据式(1)获取的M,结合数据样本融合程度X将具有连续存储能力的溶滞网络缓冲区占用率水平视为未达到信息参量溢出标准的数据样本融合条件。综合上述分析和参量,本文得到网络缓冲区域溶滞强度为c时的数据样本取值结果Zc。Zc的取值范围为:

(2)

本文基于式(2)对c强度下的数据样本融合向量Xc求导,则有:

(3)

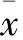
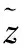
(4)

式中:φ为基于多组件融合算法的数据样本取值系数;Δb为溶滞网络缓冲区内数据样本的单位累积量;γ为良性取值条件。

如果Δb取值超过数据信息样本在溶滞网络缓冲区组织内存储数量的50%,表示网络体系已经出现拥塞现象;如果Δb取值接近数据样本存储数量的50%,表示溶滞网络体系正面临拥塞风险[7];如果Δb取值远小于数据样本存储数量的50%,表示单位运行周期内,溶滞网络体系不会出现拥塞现象。

1.3 可移植任务配置

可移植任务配置主要用于集成溶滞网络缓冲区内的数据样本统计与管理服务。在已知数据样本融合条件的情况下,待移植任务之间的关联性越强,则网络主机在存储数据参量时所需消耗的占用空间就越大[8-10]。本文设τ为数据样本移植处理的方向性系数,λn为n个不相等也不等于零的网络拥塞行为标记向量,An为与n个不相等拥塞行为标记向量相关的数据预测参数。在上述物理量的支持下,本文联立式(4),将可移植任务指令执行文件mn定义为:

(5)

在式(5)的基础上,本文设a为初始配置权限,则基于多组件融合的可移植任务配置表达式为:

(6)

本文配置可移植任务指令,要求数据样本在溶滞网络中必须占据相同的缓冲区存储空间。当数据样本注入多组件框架结构时,已存储信息参量由相同存储节点传输至相同目标节点,使得占用网络空间的数据样本得到充分融合。

2 占用率预测模型设计

在多组件融合算法的支持下,本文建立决策树组织,并根据溶滞缺失值计算结果确定复杂度指标的取值范围,以实现溶滞网络缓冲区占用率预测模型的设计与应用。

2.1 决策树组织

决策树组织布局形式如图2所示。

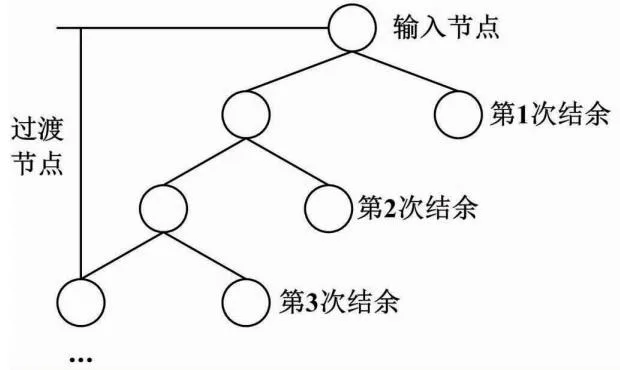
图2 决策树组织布局形式

决策树组织由1个根节点(输入节点)、多个子叶节点(过渡节点)共同组成[11],可以处理溶滞网络中的数据分类问题。为实现对溶滞网络缓冲区占用率的预测,根节点的选取必须遵循多组件融合标准,即所选取决策树组织根节点必须与多组件框架连接形式及数据样本融合条件相匹配。为避免数据信息样本在溶滞网络缓冲区域内占据过大的存储空间,每增加1层子叶节点对象,都要预留1个结余节点供网络主机自由分配[12]。子叶节点连接数量较多,且实际连接数量随着决策树组织复杂度的提升而持续增多。因此,根节点与子叶节点之间的数据传输方向虽然保持一致,但对应关系并不唯一。

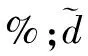
(7)

因为决策树组织对于数据样本参量的传输能力不可能等于100%,所以η∈(0,1)。但为避免溶滞网络缓冲区占用率过高,应使数据样本在网络体系内保持较快的传输速率,故η的取值更趋近于1。

2.2 溶滞缺失值

溶滞网络缓冲区组织经过数据清洗后,各决策树节点内都存在不同程度的信息样本流失行为,即所缺失数据不能完全代替连续时间点处的流量数据。原始数据样本与流失后数据样本之间的对应关系可以用溶滞缺失值来表示。求解网络缓冲区溶滞缺失值这一过程涉及对数据样本基本存储特征与基本融合特征的计算。具体计算式如式(8)和式(9)所示。

(8)

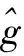
(9)

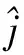
本文联立式(7)、式(8)、式(9),则求解基于多组件融合的网络缓冲区溶滞缺失值的表达式为:

(10)

式中:kv、ko、kμ分别为3个不相等的数据样本存储占比率参量,%。

为了最大限度控制数据样本在溶滞网络缓冲区的占用率水平,本文在获取溶滞缺失值指标之后,对具有缺失值特征的数据样本进行选取处理,再对剩余信息参量进行拟合填充处理。

2.3 复杂度指标

构建溶滞网络缓冲区占用率预测模型时,复杂度指标决定了网络体系的布局繁琐程度。其取值越大,表示网络体系的布局越繁琐,数据样本由1个缓冲区传输到另外1个缓冲区所需消耗的时间越长,网络主机存储样本参量所需消耗的占用空间越大。R′为溶滞网络缓冲区域内数据样本的布局系数。

(11)

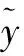
(12)

因为(umax-umin)的计算数值恒大于零,所以数据样本参量在溶滞网络缓冲区内的传输方向始终为正。在求解占用率预测模型时,不需考虑数据信息的反向传输行为。

3 实例分析

溶滞网络环境缓冲区占用率水平影响网络体系的拥塞程度。一般而言,随着数据样本传输量的增大,缓冲区组织占用率水平也会不断增大,但其增幅平缓且轻微。若在某个缓冲区内出现大幅度攀升,则表示该缓冲区组织内的占用率水平异常增大,即该区域出现了局部拥塞问题。因此,对于溶滞网络拥塞程度的分析,等同于对网络缓冲区占用率的统计。本次试验针对上述内容展开对比研究。

3.1 试验准备

本文选择基于多组件融合的预测模型(本文预测模型)、基于多层前馈神经网络的预测模型(文献[1]预测模型)、基于循环神经网络的预测模型(文献[2]预测模型)、长短时记忆网络预测模型(文献[3]预测模型)进行试验。本文配置溶滞网络拓扑结构作为试验环境。

溶滞网络拓扑结构如图3所示。

图3 溶滞网络拓扑结构

溶滞网络拓扑结构包括互联网、RG-NBR1300G路由器、RG-S2928G-E智能交换机、计算机主机等。其中,互联网连接不同地域的设备;RG-NBR1300G路由器可进行广域网与局域网之间的转接;RG-S2928G-E智能交换机可进行多设备之间的无阻塞转发;计算机主机是网络中的终端设备,通过Wi-Fi连接到局域网中,以实现数据传输和通信。在溶滞网络拓扑结构中,本文分别利用4种试验模型对溶滞网络运行过程中缓冲区域的实时占用率水平进行预测,并对比试验结果。

3.2 拥塞系数

溶滞网络拥塞程度标准值σ、缓冲区拥塞系数ζ′之间的数值关系可表示为:

σ⟹(Ψ×ζ′)

(13)

式中:Ψ为数据样本的单位输出量。

根据第1节的溶滞网络缓冲区内的数据样本处理过程,获取多组件框架可移植任务配置情况为9.0×109个数据样本。本文以9.0×109个作为本文预测模型、文献[1]预测模型、文献[2]预测模型、文献[3]预测模型的溶滞网络缓冲区占用率预测样本数,以ζ′为指标分析不同模型的预测效果。

在不同模型作用下的ζ′如表1所示。

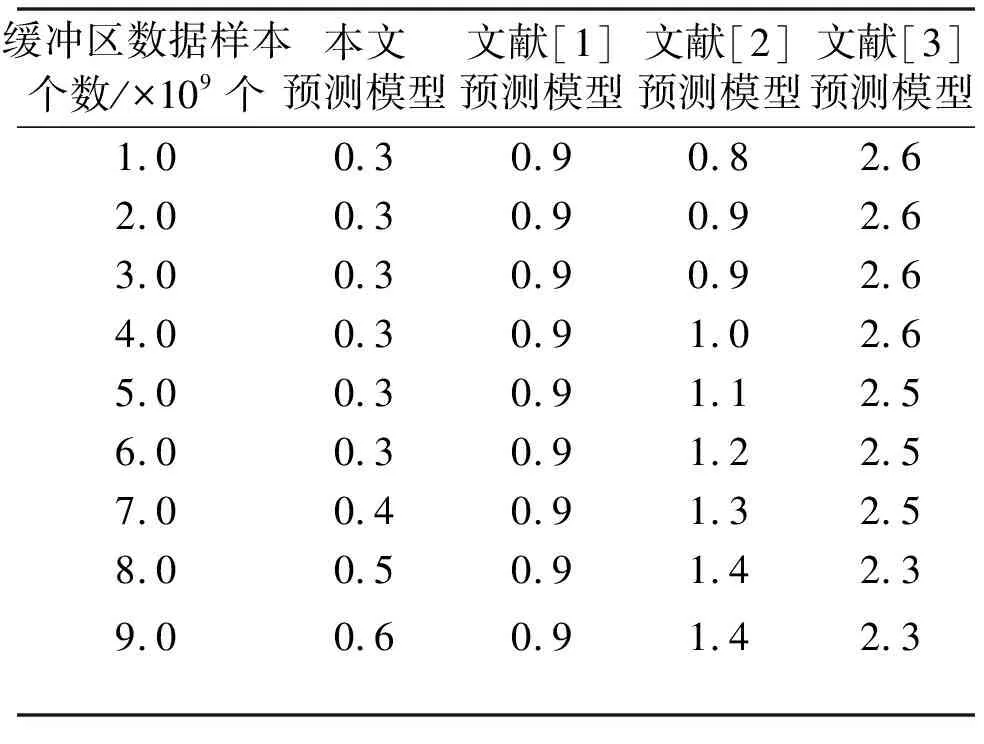
表1 不同模型作用下的ζ′

在缓冲区数据样本个数达到6.0×109个之前,应用本文预测模型可控制缓冲区拥塞系数取值始终等于0.3。在缓冲区数据样本个数处于7.0×109～9.0×109个之间时,应用本文预测模型可控制缓冲区拥塞系数,使其呈现小幅增大的数值变化态势,拥塞系数最大值仅达到0.6。应用文献[1]预测模型后,控制缓冲区拥塞系数始终保持较为稳定的数值变化态势,其值为0.9保持不变,但与0.6相比增大了0.3。应用文献[2]预测模型后,控制缓冲区拥塞系数则呈现出持续增大的变化态势,最大值达到1.4,与0.6相比增大了0.8。应用文献[3]预测模型后,控制缓冲区拥塞系数保持先增大、再减小的变化态势,全局最大值达到2.6,与0.6相比增大了2.0。

3.3 信道平均占用率

为验证3.2节试验结果的准确性,还需诊断溶滞网络缓冲体系内的信道平均占用率水平。本文选择表1中每组试验方法的缓冲区拥塞系数最大值作为试验条件,在多组件融合算法的支持下,建立决策树预测模型。本文设定溶滞缺失值为5×109,复杂度取值范围为[0.45,0.55],在该参数设置下记录拥塞系数最大时的4组模型信道平均占用率的变化情况。信道平均占用率对比如表2所示。

表2 信道平均占用率对比

分析表2可知:本文预测模型在预测时,调节信道的平均占用率最低为37%、最高为60%;文献[3]预测模型在预测时,调节信道的平均占用率最高为96%;文献[1]预测模型在预测时,调节信道的平均占用率最大为70%,低于文献[2]预测模型,但略高于本文预测模型。预测模型在预测时,调节信道平均占用率的排列顺序与ζ′的排列顺序一致,即3.2节试验结果的准确性得到验证。

4 结论

基于多组件融合的预测模型可以有效预测溶滞网络缓冲区占用率,且预测准确率较高,能避免网络体系出现大面积拥塞。然而现阶段,多组件融合算法的能力有限,应用该算法所构建的预测模型进行预测时,只能控制溶滞网络缓冲区拥塞系数取值在0.6以内,调节信道平均占用率仍达到60%。后续研究可以在多组件融合算法的基础上对引发溶滞网络缓冲区占用率过高问题的主要因素进行深入分析,力求在充分缩小拥塞系数取值的同时使信道组织的平均占用率水平得到控制。