电抗器类低电感负载雷电冲击耐压试验研究

严绍奎,赵一昆,张晓东,田 瑞

(1.国网宁夏电力有限公司营销服务中心(计量中心),宁夏 银川 750002;2.国网宁夏电力有限公司检修公司,宁夏 银川 750011)

0 引言

随着信息网络技术和微电子技术的不断发展,电气、电子设备集成化水平不断提高,雷电浪涌过电压所造成的损失也日趋严重[1]。电抗器是1种单绕组变压器,在各类场合得到广泛应用[2],如电容电压互感器中的补偿电抗器能够与电容一起实现精确计量[2]。因此,合理掌握电抗器类负载雷电冲击耐压水平等绝缘特性对于制定合理的防护措施至关重要。

雷电冲击耐压试验是电气设备绝缘测试的重要内容,是检验设备绝缘特性的主要方法之一。准确的试验波形是确保冲击电压试验可靠进行、预防设备绝缘损毁的前提。GB/T 16927.1—2011[3]给出的标准雷电冲击全波电压波形的主要特征参数有幅值过冲系数、波前时间和半峰值时间。3个特征参数的允许偏差分别为波前时间1.2 μs±30%、半峰值时间50 μs±20%、幅值过冲系数不超过10%。对于冲击电压发生器电路参数的选择,国内外学者进行了大量研究。这些研究多侧重于解决波前时间和幅值过冲的矛盾[4],通过试验和仿真等手段对冲击试验回路进行调整。优化回路布置、引入阻尼装置等方法也取得了较好的效果。相关试验表明,电抗器低压绕组等低电感负载接入回路后,雷电冲击电压波形半峰值时间达不到标准要求[5]。Glaninger等[6]对传统Marx电路进行了改进。K.Feser等[7]给出了Glaninger冲击发生回路参数选取经验式。但是上述改进措施都忽略了负载电感受不同频率和电流影响产生的阻抗变化,导致仿真电路与实际情况存在一定误差。

本文提出了基于矢量匹配法结合小脑神经网络的低电感类负载雷电冲击耐压试验仿真研究方法,讨论了负载电感对雷电冲击电压波形的影响。以电抗器为例,本文首先利用矢量匹配法结合小脑神经网络拟合预测电抗器在不同频段下的精确等值电路参数,然后根据相应等值电路参数确定合适的雷电冲击电压发生回路,最后利用电磁瞬态计算程序(electromagmetic transient calculation program,EMTP)软件仿真产生雷电冲击电压波形并分析了仿真波形特征参数的有效性。本文完整论述了电抗器雷电冲击电压试验流程及参数选取,为低电感类负载雷电冲击耐压试验设计提供参考。

1 常规雷电冲击电压器和Glaninger改进回路

常规雷电冲击电压发生器等值电路如图1所示[8]。

图1 雷电冲击电压发生器等值电路

图1中:C1为冲击发生器的电容;C2为总负荷电容(不接负载时主要考虑回路杂散电容);S为放电球隙;R1为波前电阻;R2为波尾电阻;Ll为负载电感。不考虑负载电感情况时,回路波前时间和半峰值时间近似可用式(1)和式(2)估算[9]:

(1)

式中:T1为波前时间,μs。

T2=0.73R2(C1+C2)

(2)

式中:T2为半峰值时间,μs。

研究[9]发现,当Ll处于一定范围(100～300 mH)时,可以近似忽略电感负载对冲击电压波形的影响。在实际应用中,对电抗器低压绕组等设备进行雷电冲击电压测试时,其电感经常低于下限值,故不能忽略其对波形的影响。仿真中电抗器低压绕组Ll取1 mH。未接入电感负载情况下和接入低电感负载情况下雷电冲击电压波形如图2所示。

图2 雷电冲击电压波形

由图2可知,未接入电感负载情况下,雷电冲击电压波形半峰值时间为48.2 μs。接入电感负载后,当波尾电阻为27.5 Ω时,半峰值时间为13.4 μs。即使波尾电阻增大至5 MΩ,半峰值时间仅增加至20.1 μs,也远低于标准要求的40 μs下限。这表明传统的Marx电路在接入电感负载情况下不能产生符合标准要求[3]的冲击电压波形。

传统冲击电压发生器多采用Marx多级回路[8]。工作原理遵循电容器并联充电、串联放电的原理。在正常负载的情况下,常规Marx电路产生的波形半峰值时间的增加可以通过增大R1或C1来实现。在低电感负载的情况下,增大R1对于延长波尾时间的效果不明显[8],只能考虑增大C1。这就必须额外并联充电电容器。

但冲击电压发生器最大充电电容一般限制在10～20 μF范围内。额外并联充电电容器增加了电路设计和施工的困难。因此,调整R1和C1并不能解决半峰值时间的调节难题。为解决传统Marx电路在接入低电感负载情况下冲击电压波形波尾时间不符合标准要求的问题,Glaninger等[6]对图1中的电路结构进行相应调整,将R1并联附加电感Ld来延长半峰值时间、负载并联附加电阻RP来控制波形峰值过冲系数[6]。

关于Glaninger冲击发生回路部分参数的选取,K.Feser[7]给出了相关经验式:

(3)

(4)

Ld=1.25×10-6R1

(5)

(6)

根据K.Feser经验式计算Glaninger冲击发生回路产生的雷电冲击电压波形如图3所示。

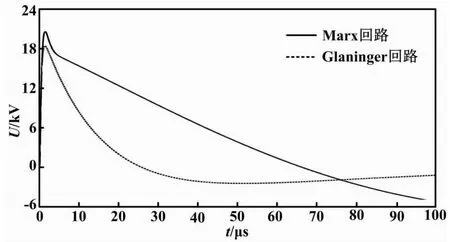
图3 Glaninger冲击发生回路产生的雷电冲击电压波形

由图3可知,根据K.Feser推荐参数选取法,Glaninger冲击发生回路产生的冲击波形存在一定畸变:峰值过冲系数为6.93%;半峰值时间为34.6 μs。虽然其较Marx电路半峰值时间有所延长,但仍未达到标准要求,因而需要对电路参数进行微调。

K.Feser推荐参数值与经试验调整后参数值如表1所示。

表1 K.Feser推荐参数值与经试验调整后参数值

由表1可知,经过对相关参数微调后,Glaninger回路产生的冲击电压波形参数符合相关标准要求,但是K.Feser经验式结合试验结果参数调整过程繁琐、耗时较长。采用Glaninger冲击发生回路后仍然需要多次调整电路参数。这主要是因为采用简单的电感元件仅能体现电感器绕组在低频段的阻抗特性,忽略了趋肤效应、铁芯的饱和效应[2],不能体现绕组在较高频段(大于10 kHz)的阻抗频变特性。因此,需要根据电抗器在不同频段的阻抗特性建立精确等效电路。

2 电抗器参数拟合

2.1 矢量匹配法

本文测量电抗器的频域特性,并利用矢量匹配法将模型阻抗与测量阻抗进行匹配,从而对电抗器等效电路参数进行拟合[10]。

电抗器的频域响应拟合采用有理函数。其具有以下近似表达形式[10]:

(7)

式中:an为未知极点;cn为留数;d和h均为实数。

由于an出现在分母中,导致由式(7)确定未知量an、cn、d和h是一个非线性问题。利用矢量匹配法定位an,使其变为已知,则式(7)转化成未知量cn、d和h的非线性问题[11]。

(8)

(9)

(10)

式(10)类似于电导、电容并联和电阻、电感串联后形成的支路。

基于矢量匹配法的电抗器等值电路如图4所示[10]。

图4 基于矢量匹配法的电抗器等值电路

式(10)和图4中电路参数与式(7)存在以下对应关系[11]:

C1i=(c1+c2)-1

(11)

(12)

(13)

(14)

表2给出了利用矢量匹配法拟合得到的电抗器等值电路参数。

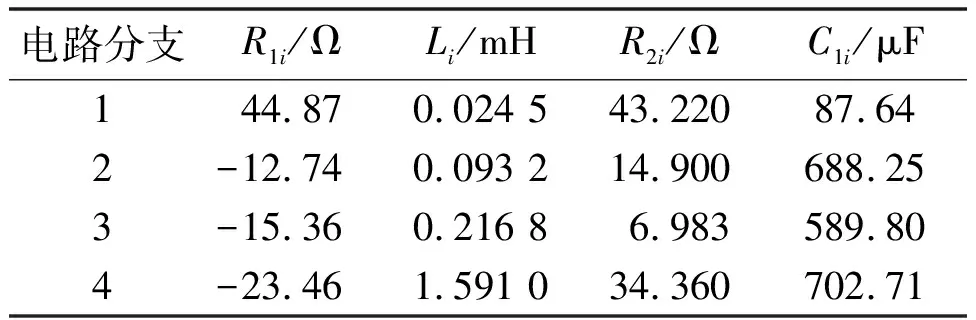
表2 利用矢量匹配法拟合得到的电抗器等值电路参数

分析表2可知,利用矢量匹配法拟合得到的电抗器等值电路电阻参数出现了负值,与实际情况不符。这是矢量匹配法受初始迭代极点影响极大的固有缺陷导致[10]的。因此,有必要对矢量匹配法拟合得到的等值电路参数作进一步优化。

2.2 小脑模型连接控制器网络参数优化

通过上述分析可知,电抗器冲击阻抗受到多个电路参数的影响,存在多个非线性的映射。其电路拟合参数的确定可以看作是一个优化问题[11]。优化的目的是尽可能降低实测阻抗和拟合阻抗之间的误差。目标函数可以用以下数学形式表达[11]:

(15)

式中:x′为未知电路参数,即C1i、R2i、Li、R1i;Zexp和Zsim为电抗器实测阻抗和拟合阻抗;k为频率点的数量。

目标函数的约束条件为电路参数取值为正。

小脑模型连接控制器(cerebellar modal articulation controller,CMAC)网络[12]具有较好的非线性逼近能力和极强的拟合能力。CMAC网络的迭代次数比一般人工神经网络少得多,能够用来对电路参数进行智能选取。CMAC网络基本结构如图5所示。

图5 CMAC网络基本结构示意图

CMAC网络采用带有2个基本映射的前馈结构。第一个映射是输入空间到联想记忆区的映射。第二个映射是联想记忆区到输出空间的映射。2个基本映射将CMAC结构划分为输入空间、联想记忆区、输出空间这3块。图5中:X为n维输入状态空间;A为联想记忆区,包括虚拟地址(control address,AC)和物理地址(physical address,AP);c1,c2,…,cn为联想单元;w1,w2,…,wn为权值表;Y为输出空间。本文通过量化、AC映射、AP映射这3个步骤,使得CMAC网络计算具有泛化能力,从而将存储联想单元的AC空间压缩到1个小得多的AP空间中。通过学习训练得到随机地址存放权值,累加求和得到CMAC网络输出[12]。

在训练过程中,如果网络输出y与期望输出e不同,则按式(16)修正权值[12]:

(16)

式中:β为学习因子;g为推广能力。

CMAC网络电路参数选取模型输入层单元数为16,分别是R1i、Li、R2i、C1i(i=1,2,3,4);输出层单元数也为16,分别是优化后的R′1i、L′i、R′2i、C′1i(i=1,2,3,4)。本文将矢量匹配法拟合得到的电抗器等值电路参数作为初始输入,归一化处理后进行训练,直至目标函数误差小于设定值或达到最大迭代次数,从而反归一化获取电抗器预测电路参数值。网络训练中,泛化常数为10、迭代次数为60、误差阈值为1%[12]。

表3给出了1组CMAC网络预测得到的电抗器等值电路参数。

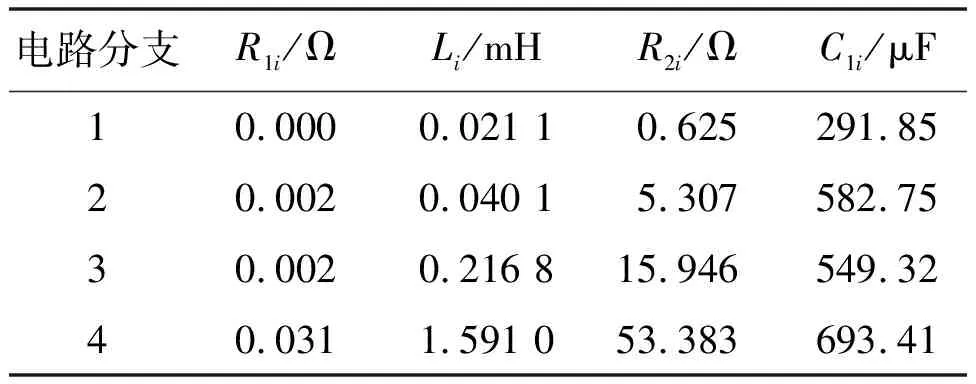
表3 CMAC网络预测得到的电抗器等值电路参数

由表3可知,利用CMAC网络预测得到的电抗器等值电路参数避免了负值出现的情况。

根据CMAC网络预测得到的1组电路参数值绘制的电抗器冲击阻抗特性曲线如图6所示。

图6 电抗器冲击阻抗特性曲线

由图6可知,利用CMAC网络预测得到的电路参数值绘制的电抗器冲击阻抗特性曲线与实测曲线一致:幅频的均方根相对误差为0.95%;相频的均方根相对误差为0.35%。该结果表明,CMAC网络电路参数预测效果较为理想。

3 仿真结果分析

电抗器雷电冲击电压仿真试验流程如图7所示。

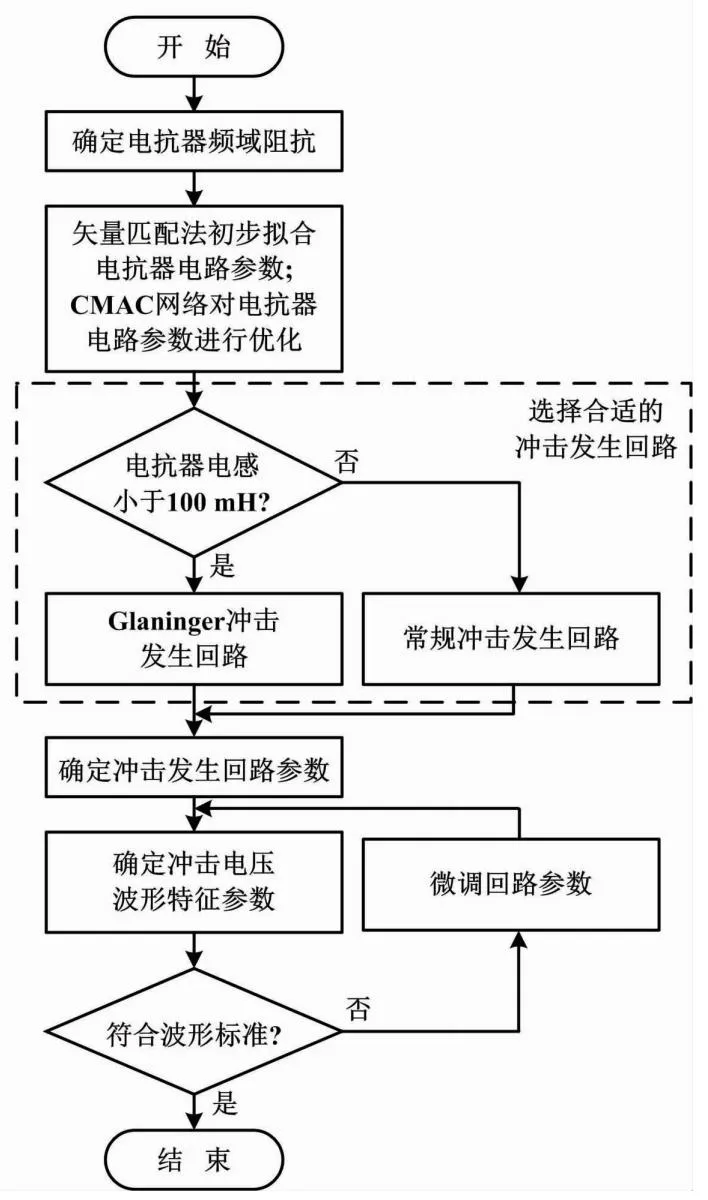
图7 雷电冲击电压仿真试验流程图

仿真试验流程的关键步骤在于先利用矢量匹配法结合CMAC网络确定电抗器高频段电感参数,再根据电感参数选择合适的冲击发生回路。当高频段电感小于100 mH时,建议采用Glaninger冲击发生回路。对大于100 mH的电感值,则选用常规冲击发生回路即可。

根据矢量匹配法,本文拟合额定电感量分别为2 mH、20 mH、200 mH的电抗器等值电路参数,并利用CMAC网络分别针对3种不同额定电感量对应的电抗器等值电路参数进行优化。每种预测得到10组电抗器电路参数,则共计产生30组仿真数据。根据30组数据仿真得到的冲击电压波形特征参数如图8所示。

图8 冲击电压波形特征参数

由图8可知,根据CMAC网络预测产生30组电抗器电路参数仿真得到的雷电冲击电压波形波前时间、半峰值时间、幅值过冲系数都处于标准规定范围内。该结果表明,利用矢量匹配法结合CMAC网络确定雷电冲击耐压发生回路参数的方法对于指导电抗器类低电感负载的雷电冲击耐压试验具有较好的效果。

4 结论

本文提出了1种电抗器类低电感负载雷电冲击耐压试验研究方法。该方法能够解决传统Marx电路接入低电感负载后冲击电压波形波尾时间达不到标准要求,而Glaninger冲击发生回路接入低电感负载后调试过程较为繁琐等问题。通过矢量匹配法结合CMAC网络方法预测电抗器电路参数,建立在不同频段下的电抗器精确等值电路模型,继而确定雷电冲击电压发生回路及参数。该方法模拟得到的电抗器冲击阻抗特性曲线与实测曲线较为一致,代入预测产生30组电抗器电路参数仿真得到的雷电冲击电压波形特征参数都处于标准规定范围内。