基于改进BiLSTM-RF的短期负荷预测研究
2024-03-14唐滨钧邝先验
唐滨钧,邝先验,吴 丹
(江西理工大学电气工程与自动化学院,江西 赣州 341000)
0 引言
随着社会经济的发展,能源能否被有效利用已成为社会生产方式重大变革的标志。我国电力市场正处于新一轮的改革阶段。国家发展改革委建议通过使用大数据技术加强对电力负荷的预测,并通过分析供需关系提高资源整合的利用率。
根据检测手段的差异,复杂电力负荷预测又可以分为以下三类方式。第一类是采用时间序列的大数据分析方法,如回归分析法[1]、卡尔曼滤波法[2]、差分自回归移动平均模型[3]等。这类方法由于利用了数据的时间相关性,在对于复杂多维的用电负荷检测时无法确保得到很好的预测精度。第二类是基于计算机智能的预测方法,如随机森林(random forest,RF)算法[4]、支持向量机(support vector machine,SVM)[5]、卷积神经网络[6]、长短期记忆(long short-term memory,LSTM)网络[7]等。这类方法对随机波动性较大的负荷数据预测具有良好的精确度,但计算速度需要进一步提升。第三类是组合预测方法。组合预测是通过挖掘各类预测方法的有效信息,避免单一方法受随机性因素的负面作用,以达到有效预测的目的。陈振宇[8]提出了通过误差倒数法将LSTM网络和极端梯度提升(eXtreme gradient boosting,XGBoost)算法组合的预测模型。组合预测模型在预测精度方面优于前两种方法。但这些方法在参变量的取值和优化,以及对短期电力负荷数据的时序特征的挖掘等方面还需要加以改进。
本文提出1种改进的双向LSTM-随机森林(improved bi-directional long short-term memory-random forest,+BiLSTM-RF)组合预测方法。该方法利用麻雀搜索算法(sparrow search algorithm,SSA)确定变分模态分解(variable mode decomposition,VMD)中的重要参变量,将原负荷数据分解成多个子序列。这不仅可以降低电力负荷的随机性和非平稳性,还可以避免人为设置参数影响预测精度。利用双向LSTM(bi-directional long short-term memory,BiLSTM)网络从正、反2个方向对子序列进行特征提取,同时添加特征注意力机制,可以进一步提升预测精度。本文采用公开数据集对该预测方法进行性能验证,并与其他预测模型进行对比。对比结果表明,本文方法的精度更高。
1 基于SSA优化的VMD
电力负荷具有非周期性和非平稳性的特点,可以通过VMD将电力负荷数据以非周期信号进行频域分解,从而把复杂多变的电力负荷数据分解成多个谐波信号。 VMD对电力负荷原始数据进行分解。其分解精度主要取决于模态分解个数k和惩罚因子α。k值设置过大,会造成过度分解;k值设置过小,会导致信息遗失。α影响每个模态分量的带宽,进而影响提取信号结果。人为设置k和α较为困难,且易导致分解结果的随机性。有研究[9]表明,SSA在群智能优化算法中的收敛速度、精度和稳定性都有较好的表现。为此,本文采用SSA优化VMD的参变量。
1.1 VMD简介
VMD可以通过确定每个模态的最佳中心频率和有限带宽对原始信号进行有效的模态分解。每个分量的带宽可以通过以下步骤估计。
①构造变分问题。
将原始电力负荷数据T分化为k个模态,且各模态在其中心频率的带宽之和最小,同时各模态之和与原数据相等。VMD约束变分模型为:
(1)
式中:∂t为冲激函数;uk为各模态函数;ωk为各模态中心频率。
②采用拉格朗日乘子λ和α寻找约束变分问题的最优解。
扩展的拉格朗日表达式为:
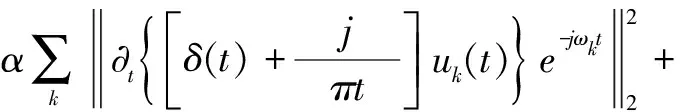
(2)
③各模态函数和中心频率为:
(3)

1.2 基于SSA优化的VMD算法
SSA寻优VMD参数是根据最小样本熵[10](sample entropy,SE)原理确定k和α。其步骤如下。
①将给定的长度为N的时间负荷序列X={x(1),x(2),…,x(N)}构造成m维矢量,即:
X(i)={x(i),x(i+1),…,x(i+m-1)}
(4)
式中:i=1,2,…,N-m+1。
②定义X(i)与X(j)间的最大距离为D,即:
(5)
③给定阈值r(r>0),统计D (6) ④对由式(6)得到的结果求平均,即: (7) ⑤将维数m加 1,重复步骤①~步骤④。 ⑥对于N′个样本的时间负荷序列,其SE值为: (8) SE值越低,则信号复杂度越低、自相似度越高。本文将SE趋于稳定的转折点作为VMD的分解次数,以避免过度分解。 BiLSTM由正、反2个方向的LSTM模型组成。在对时间序列预测时,不同于由前到后进行训练的传统单向神经网络,BiLSTM通过双向网络对过去和未来的隐藏层进行递归反馈,充分挖掘过去和未来时刻的负荷数据与当前数据的内在联系,从而更好地提取内部特征、进一步提高对模型精度和数据的利用率。BiLSTM模型如图1所示。 图1 BiLSTM模型 由图1可知,BiLSTM相较于LSTM增加了由未来到过去的数据传输方向,并且与位于正、反2个方向之间的隐藏层互相独立。其相比于LSTM模型展现出了更加优越的性能。 注意力机制如图2所示。 图2 注意力机制 在深度学习中,注意力机制可以通过自适应分配不同信息的权重,提高模型的特征挖掘能力。本文将注意力机制引入BiLSTM网络[11],因此在提取输入数据特征时,可以只提取更为关键的特征,而减少甚至删除其他次要特征。由此可以提升模型预测效率和准确性,并且提高解决信息过载的能力。 RF是基于Bagging的高效、灵活的算法,是高度集成的机器学习算法。RF的基本理论是从原始样本中随机抽取多个样本时,需要建立某种形式的独立训练集,进而在建立回归决策树时使得每个决策树都单独产出1个预测值。估计结果的最终取值则为每个决策树产出的预测值的平均数。 随机森林回归(random forest regressor,RFR)是基于1组决策树组合的模型。本文假设从独立同分布的随机向量(X,Y)中抽取训练集,通过泛化误差判断模型的预测能力,则任一数值预测值h(x)的均方泛化误差为: EX,Y=[Y-h(X)]2 (9) 本文假设t棵决策树的对应随机向量为θt,则当t趋近于无穷时,有: (10) (11) 对于所有的θ,有: (12) 式中:λ为残差Y-h(X,θ)与Y-h(X,θ′)的相关系数。 θ与θ′相互独立。由式(12)可知,RF通过相关系数λ降低了决策树的平均泛化误差。 本文将模型得到的预测值与测试集的真实值进行对比。模型预测由决定系数(R2)、均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、平均绝对百分误差(mean absolute percentage error,MAPE)这4个回归评价指标进行评判。 (13) 根据R2的取值可以判断模型的优劣。R2的取值范围为0~1。R2越接近1,则说明模型效果越好。 (14) 式中:Rmse为RMSE值。 由式(14)可知,RMSE表示数据点的离散程度。模型精度越高,则Rmse的数值越小。 (15) 式中:Mae为MAE值。 由式(15)可知,Mae越小,则模型的精确度越高。 (16) 式中:Mape为MAPE值。 如式(16)可知,Mape越小,则模型的精确度越高。 基于SSA优化VMD的+BiLSTM-RF预测模型如图3所示。 图3 +BiLSTM-RF预测模型 优化的负荷预测模型主要分为4个步骤。 ①参数优化。通过SSA算法,确定VMD的模态分解个数k值和惩罚因子α。 ②模态分解。模态分解将历史负荷X′={x1,x2,…,xN}导入经过SSA优化的VMD,构成预测模型输入变量Xk={x(1),x(2)…,x(k)},以降低电力负荷的随机性和非平稳性。 ③特征提取。采用具有注意力机制的BiLSTM网络对各分量进行特征提取。 ④负荷预测。负荷预测将BiLSTM提取出的各模态内部特征输入RF模型,得到各分量模态的预测值Yk={y(1),y(2)…,y(k)};叠加重建后,得到最终的负荷预测结果。 数据集是某地区2014年11月1日至2015年1月10日每天间隔15 min采集的用电负荷数据。试验将2014年11月1日至12月31日的5 856个数据作为训练样本、2015年1月1日至1月10日的960个数据作为测试样本。试验平台装有NVDIA GeForce GTX 1650 Ti的服务器。编程采用Python和Matlab实现。BiLSTM-RF模型通过tensorflow建立。 SSA优化算法的初始设置如下:种群数量为20个;迭代次数为30次;k∈[3,8];α∈[100,5000]。 VMD经过SSA寻优后的参数组合[k,α]为[4,3 034];各固有模态函数(intrinsic model function,IMF)分量的SE分别为0.001 6、0.000 9、0.014 1、0.011 8。 VMD分解后的子模态曲线如图4所示。 图4 子模态曲线 4.3.1 滑窗宽度对模型的影响 本文采用滑动窗口方法进行预测。为提高模型预测精度,本文对滑动窗口的参数进行了对比分析。 不同滑窗宽度下的预测误差对比如表1所示。 表1 不同滑窗宽度下的预测误差对比 由表1可知,当滑窗宽度为5时,+BiLSTM-RF模型在各精度分析指标都有较好的表现。 4.3.2 注意力机制对模型的影响 为比较注意力机制对特征提取优化后的+BiLSTM-RF组合模型的预测能力的影响,本文在其他条件参数一致的情况下,对比注意力机制添加前后组合模型的预测性能。注意力机制对模型性能的影响如表2所示。 表2 注意力机制对模型性能的影响 由表2可知,当滑窗宽度为5时,通过添加注意力机制能提高本文所提组合模型的精度。 4.3.3 与传统预测模型对比 为体现本文模型短期负荷预测的性能,本文将所提+BiLSTM-RF与常用的电力负荷预测中的LSTM和门控循环单元(gated recurrent unit,GRU)、SVM、未经优化的BiLSTM-RF等预测模型进行对比。不同模型误差对比如表3所示。 表3 不同模型误差对比 不同模型预测曲线如图5所示。 图5 不同模型预测曲线 本文构建了基于SSA优化的模态分解后的+BiLSTM-RF短期负荷预测组合模型。本文首先利用最小SE原理确定模态分解的k和α,将原始电力负荷数据分解为k个模态;然后利用BiLSTM网络和注意力机制从正、反2个方向迭代循环提取有效特征信息;最后利用RF模型进行预测。本文以某地区电力负荷数据作为实际算例进行了验证分析。相较于传统机器学习模型,本文提出的+BiLSTM-RF组合模型有以下优点:①考虑了负荷特征的时序特征;②降低了电力负荷数据随机性与非平稳性;③对模型内部参数的取值和优化有进一步提高;④在短期电力负荷的预测方面与传统预测方法相比有更好的表现。但是由于短期负荷的预测还受气温 、降雨、湿度等气候因素的影响,后续可以考虑在多维参数的情况下进一步提升短期负荷预测模型的精度。2 基于BiLSTM-RF的预测模型
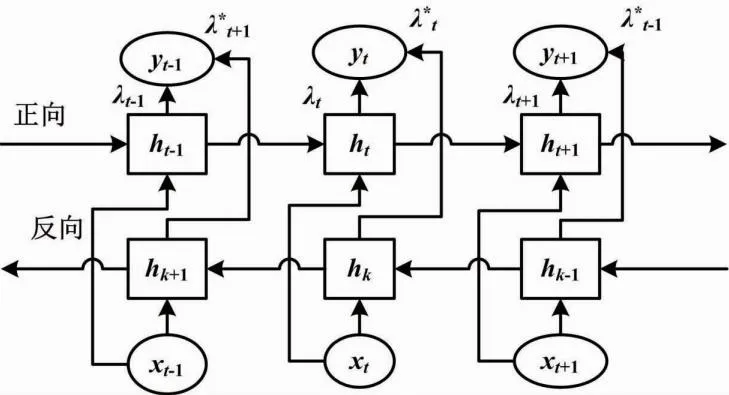
2.1 BiLSTM网络

2.2 注意力机制
2.3 RF网络
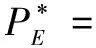
2.4 模型精度分析
3 短期负荷预测模型
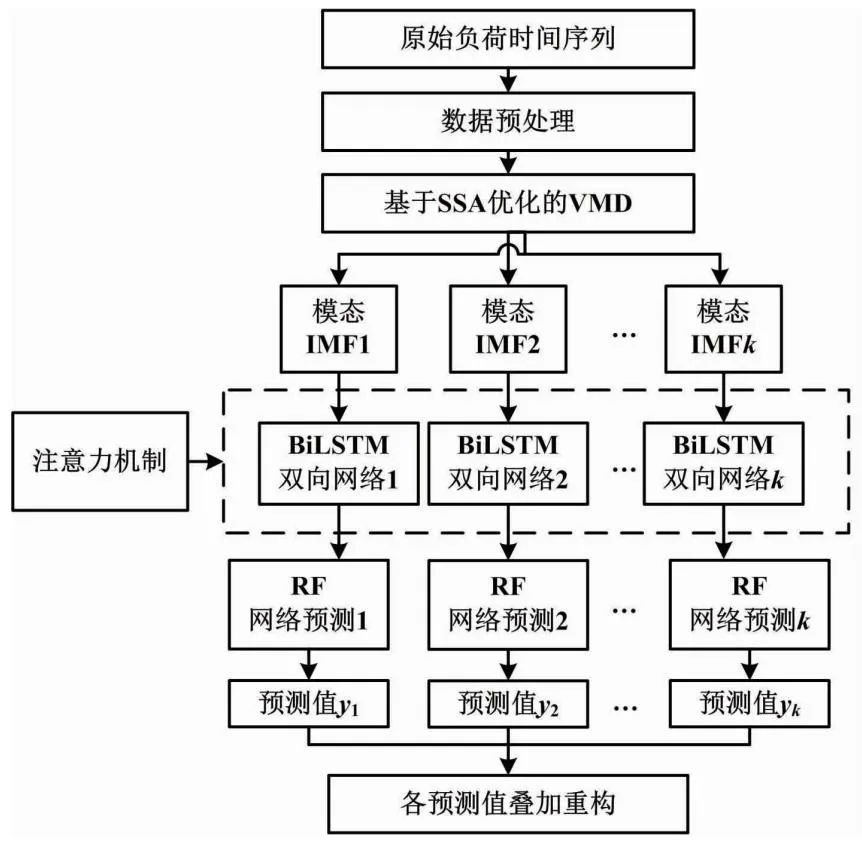
4 试验验证
4.1 试验数据与平台
4.2 负荷序列分解
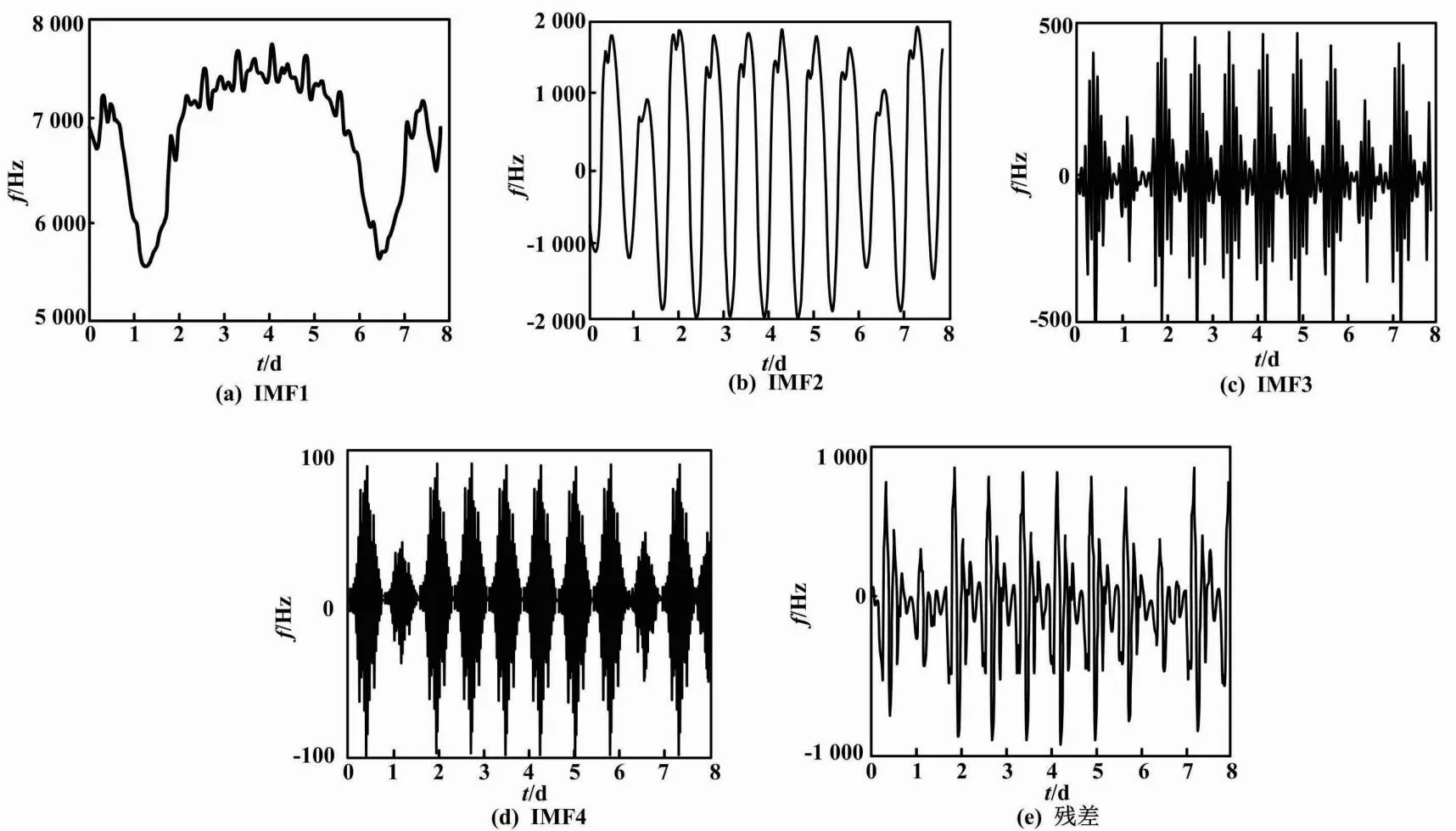
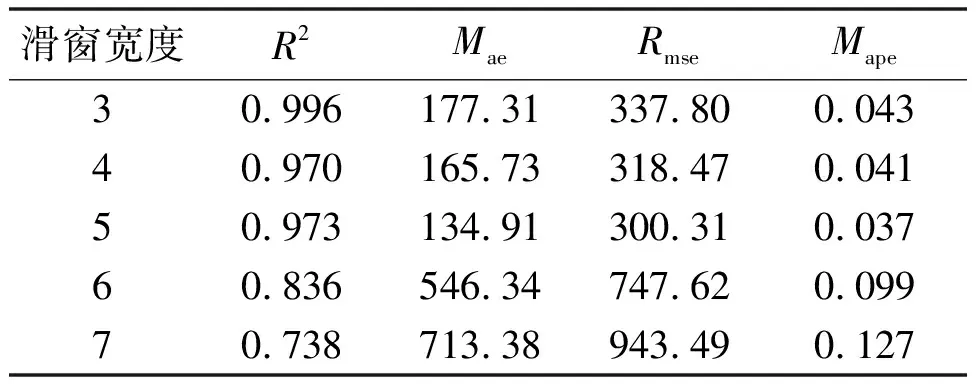
4.3 模型性能评估与算例分析
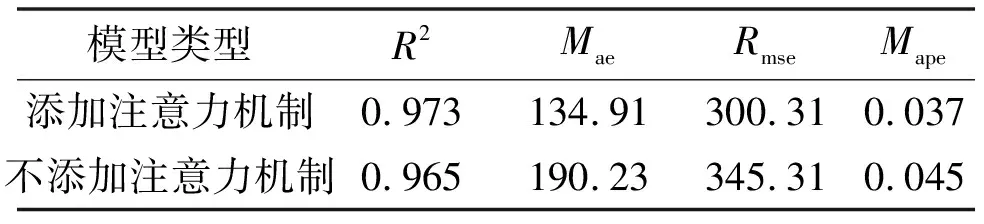

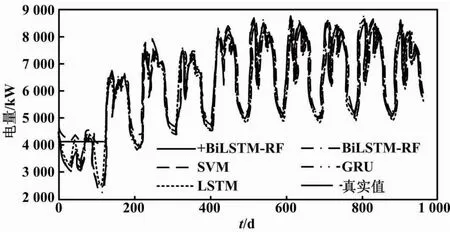
5 结论
