双向驱动井径测井仪推靠系统工作行为分析

席文奎，陈虎子，隽鸿科，耿东恒，魏航信，孙文

(1.西安石油大学机械工程学院，陕西西安 710065；2.陕西航天时代导航设备有限公司，陕西宝鸡 721035)

0 前言

在油气井开采过程中，拥有先进高精度测井技术的测井仪是评估套管径向胀裂和裸眼井井壁坍塌程度的关键测量仪器[1]。现如今，井径测井仪主要分为套管井测量和裸眼井测量，套管井主要测量套管壁厚变化导致的局部损伤，裸眼井主要测量因钻井液侵蚀、冲刷和钻头碰撞导致的各个地层段井径大小变化情况。

随着油气井开采深度不断增加、水平井和大斜度井的增多，对测井装备的测量性能和可靠度提出更高要求，国内许多学者围绕测井仪的结构设计进行改进和创新，王会来等[2]设计了一种测量范围为250～400 mm的测井仪推靠系统，运用力学平衡理论和仿真软件进行机构性能分析，检验新机构的可行性；宋红等人[3]提出了一种无附加载荷、井壁对极板冲击更小的新型分动式推靠机构，运用矩阵解析法和ADAMS仿真对推靠机构各阶段的运动进行分析及验证；陈国栋等[4]将磁阻传感器用于测量裸眼井的六臂井径测井仪，通过分析误差影响因素得出其具有更高的测量精度和分辨率；吴超等人[5]设计了一种新型液压驱动结构作为测井仪动力源，通过对其设计关键点进行分析计算及地上加载模拟实验，证明了液压系统设计方法的正确性和可行性；任涛等人[6]设计了一种新型六臂井径测井仪推靠系统，通过对3种不同轮廓线推靠臂凸轮进行运动分析及仿真，选取最优的推靠臂线型结构。综上所述，现存井径测井仪多数采用单一动力源，单向驱动推靠结构，存在单边驱动速度集中和初始运动冲击等问题。

本文作者提出了具有双向驱动特征的井径测井仪，可解决单向驱动井径测井仪存在的上述问题，并对其推靠系统进行了运动学理论求解和工作行为分析(运动性能和测量性能仿真)。

1 双向驱动井径测井仪结构模型及工作原理

双向驱动井径测井仪结构模型如图1所示，主要包括多动力源模块、传动模块、双驱动推靠系统模块。其工作原理为：多动力源模块(6个电机)为整体机构运行提供动力，动力经传动模块(联轴器、传动杆、传动自锁装置)传递给双驱动推靠系统模块(大小径丝杠驱动、推靠臂、支撑臂、推靠杆)，通过控制推靠系统双驱动速度匹配关系将驱动速度进行分解，使双驱动结构以不同的双向速度进行平稳相向或相背运动，实现测井仪推靠系统的打开和收缩功能。

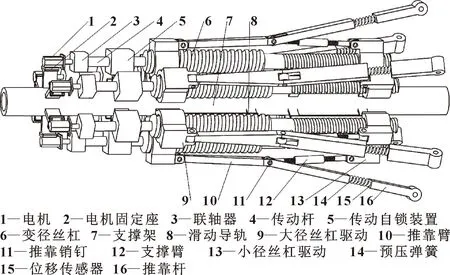
图1 双向井径测井仪物理结构模型

测井仪井下作业状态主要分为打开状态、测量状态和收缩状态，其具体实施过程如下：

(1)打开状态。电机顺时针旋转，同时传动自锁装置关闭，动力经联轴器和传动杆传给变径丝杠，丝杠旋转带动大小径丝杠驱动沿滑动导轨做相向直线运动，支撑臂和推靠臂在大小径丝杠驱动的作用下向外扩张，当推靠杆接触井壁时，电机带动丝杠继续旋转，预压弹簧开始储能，当位移传感器检测到预设的储能位移并反馈信号时，电机将停止转动，传动自锁装置打开。

(2)测量状态。测井仪在牵引绳的作用下向上提升，预压弹簧提供弹力使得推靠杆始终紧贴井壁，随着井径变化带动位移传感器运动，将井径的变化规律转化为电子信号并绘制井径轮廓曲线。

(3)收缩状态。传动自锁装置关闭，电机逆时针转动，大小径丝杠驱动和推靠杆回归初始位置后，电机停止转动。

2 双向驱动井径测井仪推靠系统运动学分析

本文作者采用复数矢量法对双向驱动井径测井仪平面连杆机构进行运动矢量化求解。通过对井径测井仪连杆机构进行矢量化表征，将连杆机构转化为封闭矢量几何模型，以复数形式表示测井仪连杆机构的封闭矢量位置方程，将位置方程对时间求一次和二次导数[7]，得到其速度和加速度方程，获取运动性能参数。

2.1 建立推靠系统数学几何模型

针对测井仪物理结构建立其推靠系统几何模型，并采用复数矢量法进行表征，如图2所示。其中，A′O′、B′O′、O′C′、AO′、A′C′、AC′对应的矢量分别为l1、l2、l3、S1、S2、S3，其矢量模分别为l1、l2、l3、S1、S2、S3。SA、SB对应矢量SA和SB，分别代表大小丝杠驱动的距离，SC对应矢量SC，代表大小径丝杠驱动之间的距离。

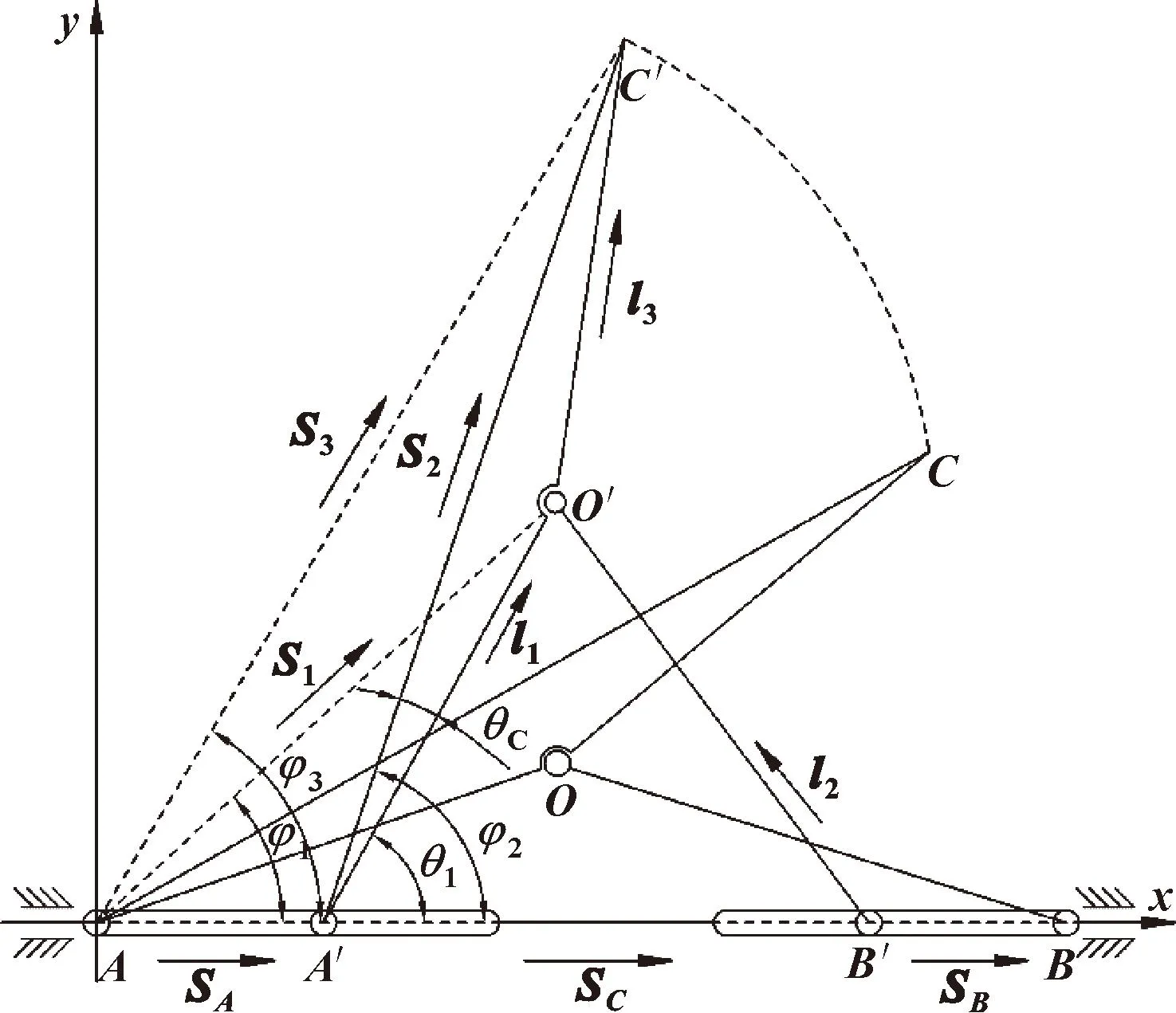
图2 推靠系统矢量化几何模型

在实际工作过程中，建立双驱动系统输入参数(速度、位移)与测井仪推靠系统运动输出参数(位移、速度、加速度)之间的数学关系。以大径丝杠驱动初始位置点A为原点，建立笛卡尔直角坐标系[8]，假设大小丝杠双驱动的输入速度分别为vA和vB，可根据式(1)—(3)求得SA、SB、SC。

SA=vAt

(1)

SB=vBt

(2)

SC=lAB-SA-SB

(3)

式中：vA为大径丝杠驱动速度，mm/s；vB为小径丝杠驱动速度，mm/s；t为运动时间，s；lAB为大小径丝杠驱动之间的初始距离，mm。

在△A′O′B′中，根据余弦定理，可求得推靠臂l1的幅角θ1。

(4)

令θ1=arccos(A)，对式(4)进行一次和二次求导，如式(5)—(6)所示，可得到幅角θ1的角速度ωθ1和角加速度αθ1。

(5)

(6)

由图2可知，推靠臂l1的幅角θ1与中间矢量S2的幅角φ2有如式(7)所示的关系，且求导得出两幅角的角速度与角加速度相等，即ωφ2=ωθ1，αφ2=αθ1。

φ2=θ1+θC

(7)

式中：θC为∠C′A′O′的大小，rad。

2.2 推靠系统矢量位移分析

(1)在△AA′O′中，运用复数矢量法分析推靠销钉点O′的位置和中间矢量S1及其幅角φ1。根据三角形矢量和为零，建立封闭矢量方程如式(8)所示：

S1=SA+l1

(8)

将上式用复数形式表示：

S1eiφ1=SA+l1eiθ1

(9)

上式S1和φ1为未知量，其余量均为已知量。根据欧拉公式，由实部虚部分别相等可得：

(10)

解出未知量：

(11)

推靠销钉点O′沿坐标轴的位移分量为

(2)以矢量△AA′C′分析推靠杆端口点C′的位置和中间矢量S3及其幅角φ3。建立封闭矢量方程如式(12)所示：

SA+S2=S3

(12)

将上式用复数形式表示：

SA+S2eiφ2=S3eiφ3

(13)

根据欧拉公式，由实部虚部分别相等可得：

(14)

解出未知量：

(15)

推靠杆端口点C′沿坐标轴的位移分量为

2.3 推靠系统矢量速度分析

(1)以矢量△AA′O′分析推靠销钉点O′的线速度vS1(方向与S1相同)及其幅角角速度ωφ1。

将式(9)对时间求导数得：

vS1eiφ1+S1ωφ1ieiφ1=vA+l1ωθ1ieiθ1

(16)

上式vS1和ωφ1为未知量，其余量均为已知量。由欧拉公式展开可得：

vS1+S1ωφ1i=vA(cosφ1-isinφ1)+l1ωθ1i[cos(θ1-φ1)+isin(θ1-φ1)]

(17)

解出未知量：

(18)

(2)以矢量△AA′C′分析推靠杆端口点C′的线速度vS3(方向与S3相同)及其幅角角速度ωφ3。

将式(13)对时间求导数得：

vA+S2ωφ2ieiφ2=vS3eiφ3+S3ωφ3ieiφ3

(19)

由欧拉公式展开可得：

S2ωφ2i[cos(φ2-φ3)+isin(φ2-φ3)]+vA(cosφ3-isinφ3)=vS3+S3ωφ3i

(20)

解出未知量：

(21)

推靠杆端口点C′在空间做无规则的曲线运动，将无规则的曲线运动分解为多种规则曲线运动，可求得运动参数的准确表达式。如图3所示，推靠杆端口点C′的运动曲线可分解为沿CD的圆周运动和沿DC′的直线运动，将线速度与圆周切向速度vτ(大小为S3ωφ3，方向与vS3垂直)沿坐标轴进行分解可求得推靠杆端口点C′速度分量。

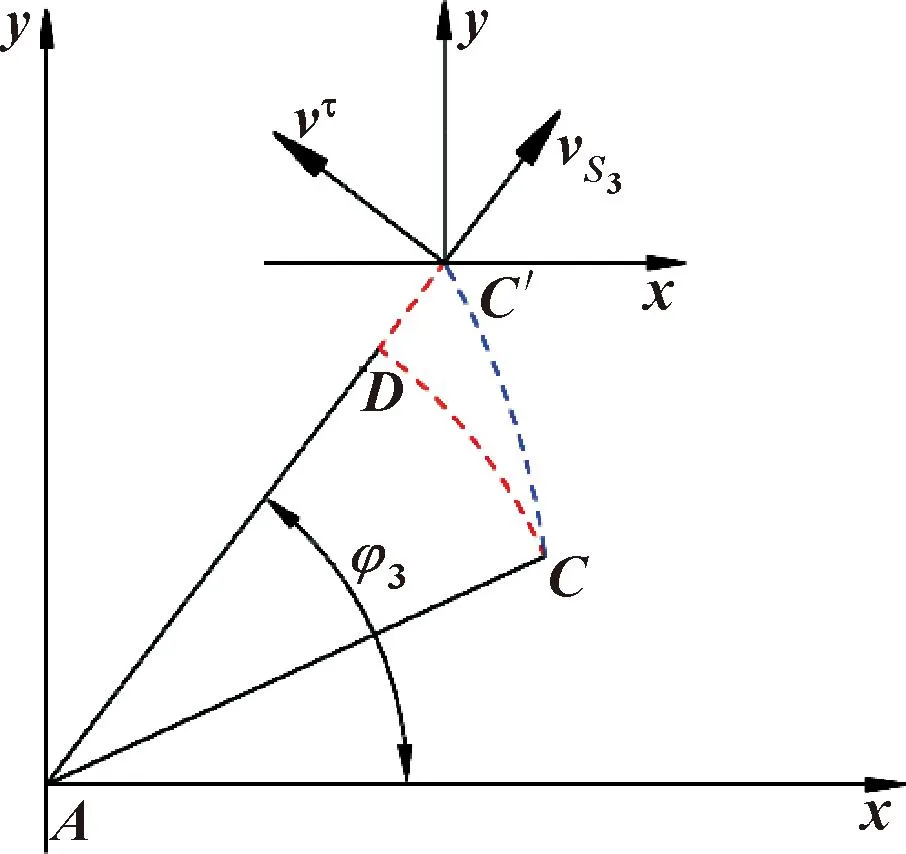
图3 速度矢量分解

推靠杆端口点C′沿坐标轴的速度分量：

vx=vS3cosφ3-S3ωφ3sinφ3

vy=S3ωφ3cosφ3+vS3sinφ3

同理可得，推靠销钉点O′速度沿坐标轴的速度分量为

vx=vS1cosφ1-S1ωφ1sinφ1

vy=S1ωφ1cosφ1+vS1sinφ1

2.4 推靠系统矢量加速度分析

(1)以矢量△AA′O′分析推靠销钉点O′的线加速度aS1(方向与vS1相同)及其幅角角加速度αφ1。

将式(16)对时间求导数得：

(22)

上式aS1和αφ1为未知量，其余量均为已知量。由欧拉公式展开可得：

(23)

解出未知量：

(24)

(2)以矢量△AA′C′分析推靠杆端口点C′的线加速度aS3(方向与vS3相同)及其幅角角加速度αφ3。

将式(19)对时间求导数得：

(25)

由欧拉公式展开可得：

(26)

解出未知量：

(27)

推靠杆端口点C′同时做圆周运动和径向直线运动，在运动过程中会产生科氏加速度，方向垂直于角速度方向和线速度方向。其加速度矢量分解如图4所示，将线加速度aS3、圆周切向加速度aτ、圆周法向加速度an和科氏加速度aC(大小为2vS3ωφ3，方向与vS3垂直)沿坐标轴进行分解可求得点C′加速度分量。

图4 加速度矢量分解

推靠杆端口点C′沿坐标轴的加速度分量：

同理可得，推靠销钉点O′沿坐标轴的加速度分量为

2.5 双向驱动推靠系统数据流模型分析

数据流表示输入与输出之间的数据流动过程。通过使用箭头表示数据的流动方向，使用标签描述数据流的内容，可以清晰地表示系统的功能过程和数据流动路径。

本文作者基于数据流架构建立双驱动推靠系统功能模型，对双驱动推靠系统运动分析过程进行表征，如图5所示。该功能模型包括4个功能：输入功能、模型功能、输出功能和匹配功能。

图5 双驱动推靠系统模型功能图

(1)输入功能。以双驱动速度(vA、vB)为输入参数，采用复数矢量法对双驱动运动参数进行矢量化表征。

(2)模型功能。建立双驱动推靠系统矢量几何模型，搭建输入参数(速度变量、基本初始定量)与输出参数之间的数据桥(中间变量)，为双驱动推靠系统输出模块提供数据保障。

(3)输出功能。输出关键点(点C′、点O′)沿坐标轴方向上的运动参数分量。

(4)匹配功能。以输出关键点(点C′、点O′)y方向运动参数为基础，对和速度与y方向运动参数进行匹配特性分析。

通过对4个功能模块的分析，完整重现双驱动推靠系统运动参数矢量化求解过程，为后续测井仪推靠系统研究做理论铺垫。

3 实例分析

3.1 实例基本参数

借鉴实际工程中SL4209型井径测井仪结构参数(最大井眼尺寸406 mm)，设计制定了双向驱动井径测井仪基本结构参数，如表1所示。

表1 双向驱动井径测井仪基本结构参数

3.2 运动曲线

在实际测井过程中，推靠杆端口点C′和推靠销钉点O′运动学参数是表征测井仪测量性能和运动平稳性能的关键指标，中间矢量S1和S3的幅角是影响推靠系统整体运动性能的关键因素。进一步分析两点(点C′、点O′)和矢量S1和S3幅角的运动变化规律，可直观评判新型井径测井仪推靠系统的运动性能。

由上文分析可知，推靠杆端口点C′和推靠销钉点O′运动学关键参数直接决定了测井仪推靠系统的运动稳定性，下文进行点C′和点O′运动学关键参数的计算设计[9]。以大小径丝杠驱动速度和推靠系统基本参数为输入，代入式(1)(2)(4)(7)(11)(16)(19)(22)(25)(28)中，求解出中间矢量S1和S3的模长和幅角(变量)，进一步代入运动分量公式中，求解输出推靠杆端口点C′和推靠销钉点O′的运动分量参数。

推靠杆端口点C′位移、速度和加速度运动曲线如图6所示。可以看出：(1)推靠杆端口点C′的位移、速度和加速度曲线较为平滑，表明推靠杆在作业时不会出现因速度巨变而导致的运动冲击。(2)推靠杆端口点C′加速度在x和y方向上的分量随着时间的增长趋向于零，表明推靠杆在实际运行中具有良好的平稳性。

图6 推靠杆端口点C′运动曲线

推靠销钉点O′位移、速度和加速度运动曲线如图7所示。可以看出：(1)推靠销钉点O′的位移、速度和加速度曲线较为平滑，表明推靠销钉具有平稳的运动性能。(2)与推靠杆端口点C′运动曲线相比，点O′和点C′在y方向上的运动参数分量有相似的规律和趋势。(3)在x方向上，点O′的位移分量在10.6 s时，由减小趋势转变为增大趋势，点O′的速度分量在这一时刻由负变正，表明点O′在x方向上做往复运动。

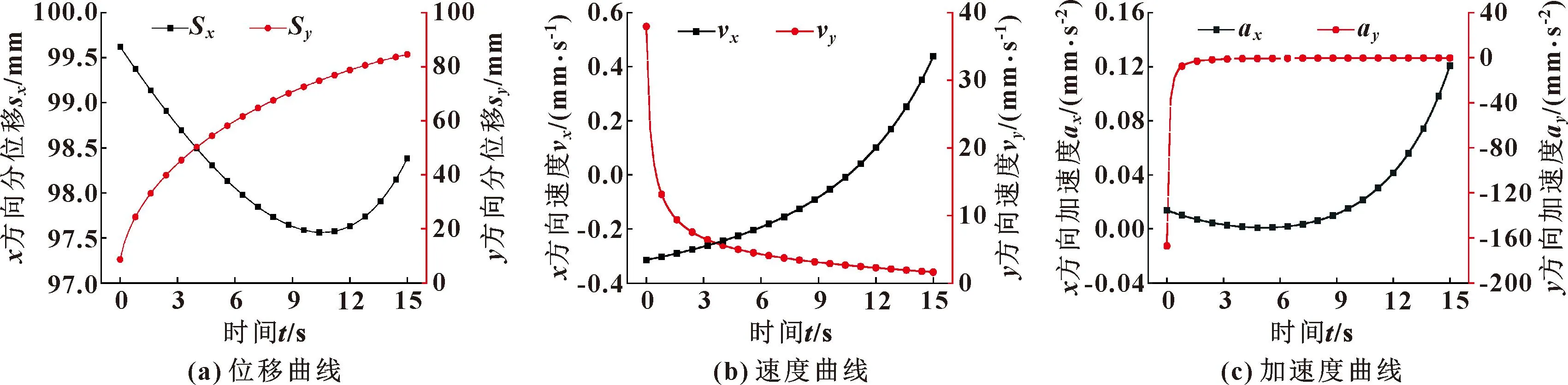
图7 推靠销钉点O′运动曲线

幅角φ1运动曲线如图8所示，幅角φ3运动曲线如图9所示。

图8 幅角φ1运动曲线

图9 幅角φ3运动曲线

由图8、9可以看出：

(1)对比幅角φ1和φ3的运动曲线，其运动参数随着时间的增长，有相似的运动变化规律。

(2)幅角φ1和φ3的运动曲线十分光滑，其角加速度在0.8 s之后趋向于零，表明推靠系统在实际运行时，推靠臂运动平缓，不会出现剧烈摆动。

3.3 双驱动匹配特性研究

上文以大小丝杠驱动速度为定值输入，对推靠杆端口点C′和推靠销钉点O′的运动规律进行了分析讨论。下文将通过改变驱动速度vA和vB，对丝杠驱动速度(变量)与推靠杆端口点C′y方向运动参数进行匹配特性研究。

以速度vB为定值(5 mm/s)，研究驱动速度vA(变量)对点C′y方向运动参数的影响，如图10所示；以速度vA为定值(5 mm/s)，研究驱动速度vB(变量)对点C′y方向运动参数的影响，如图11所示。

图10 速度vA变化的位移曲线

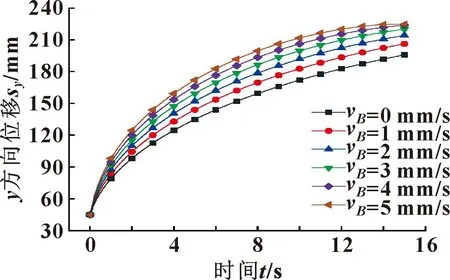
图11 速度vB变化的位移曲线

由图10可以看出：随着速度vA的增加，y方向位移(点C′)也随之增加，并且其增长率逐渐下降。比较两幅速度变化的位移曲线图可知：驱动速度vA与vB对y方向位移(点C′)的变化具有相同影响，以相同幅值改变vA或vB(同时增大或减少)，y方向位移曲线具有相同的变化量。

受推靠杆端口y方向位移的变化规律启发，分别以相同幅值增加vA和减少vB，保持驱动速度vA和vB之和不变，进一步研究双驱动速度与推靠杆端口点C′y方向位移之间的匹配特性关系，并绘制y方向位移(点C′)曲线，如图12所示。

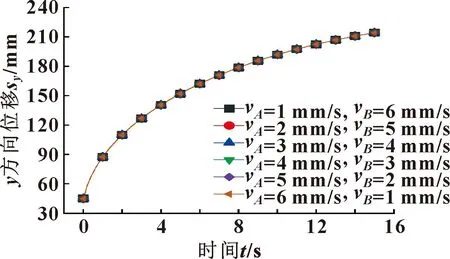
图12 速度变化的位移曲线

由图12可以得出结论：y方向位移(点C′)与vA和vB之和成正相关关系，与vA和vB本身大小无关。无论速度vA和vB如何变化，只要保持vA和vB之和不变，就可得到唯一的y方向位移(点C′)运动曲线。反之，y方向位移(点C′)轨迹确定时，其所对应的驱动和速度也唯一确定。

推靠杆端口y方向位移轨迹与所对应的驱动和速度确定时，采用传统单向丝杠驱动的缺点为只能提供两种速度匹配组合，一侧固定(速度为0)，另一侧速度与驱动和速度相等。采用双向丝杠驱动的优点在于提供多种速度匹配组合，两侧速度可以任意取值。相较于将和速度完全施加在一侧的单向驱动，双向驱动提供多种双侧速度组合方式，降低单侧速度集中，减少初始运动冲击，保持机构平稳运行。

4 测井仪推靠系统工作行为仿真分析

4.1 运动性能仿真

由双向井径测井仪物理结构模型(图1)可知，6个测井推靠模块呈圆周均匀分布，其物理结构模型和矢量化几何模型完全相同。通过简化推靠模块物理结构模型[10]，以ADAMS为载体建立推靠系统仿真模型，对其运动性能进行仿真，验证上述推靠系统运动理论结果的正确性及合理性。

4.1.1 建立仿真模型

参照表1基本结构参数建立推靠系统简化仿真模型并对其进行材料属性添加[11]，结合各构件间的实际连接关系创建相应的约束、运动副和加载驱动，完成测井仪推靠系统仿真模型的建立。

(1)创建约束和运动副

由于仿真模型是以支撑架中心为对称轴的上下对称结构，其上部分的约束和运动副与下部分相同，所以只描述上部分推靠系统的约束和运动副，如表2所示。

表2 推靠系统约束与运动副

(2)加载驱动

以变径丝杠与地面之间的转动副为基础，建立仿真模型旋转驱动[12]，为双驱动推靠系统提供动力，其驱动函数为360d×time。

测井仪推靠系统运动仿真模型，如图13所示。

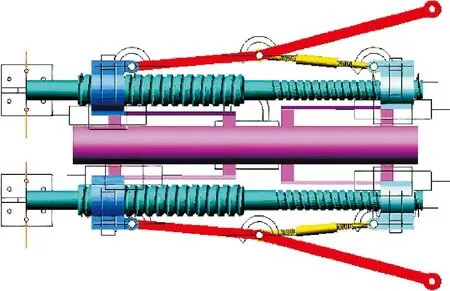
图13 测井仪推靠系统运动仿真模型

4.1.2 仿真测试分析

设置仿真终止时间为15 s，仿真步数为100。

推靠杆端口沿坐标轴方向的位移、速度和加速度曲线，如图14、15所示。

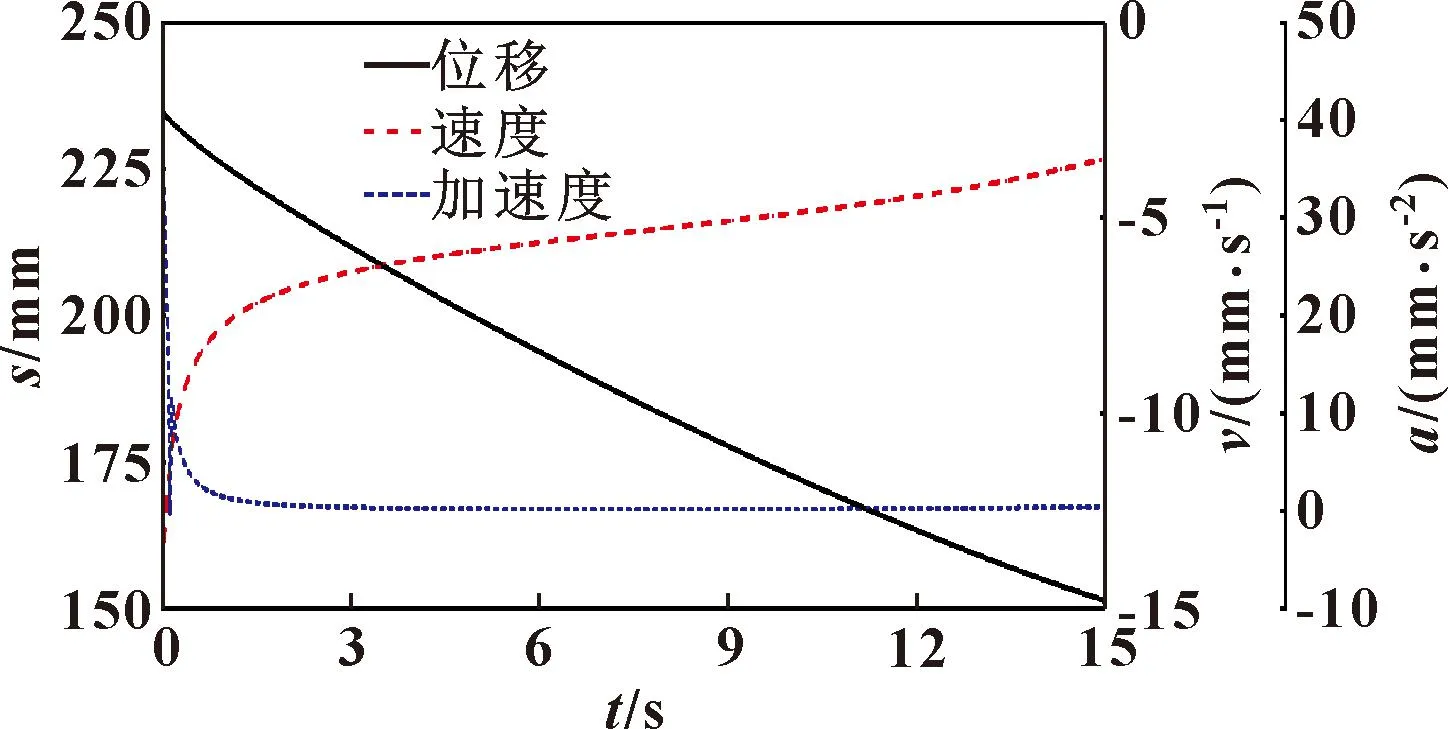
图14 推靠杆端口x方向运动曲线

由图14、15可以看出：(1)推靠杆端口x和y方向上位移和速度曲线较为光滑，但其两方向上的加速度分量在模型运动初期均发生突变。(2)在0～1 s内，两方向上的位移变化缓慢，速度与加速度剧烈变化(减少)，在1 s之后，运动参数均处于缓慢变化阶段。(3)相较于理论曲线(图6)，推靠杆端口运动参数的变化规律和总体趋势与理论值基本一致，验证了推靠杆端口运动理论结果的正确性。

推靠销钉沿坐标轴方向的位移、速度和加速度曲线，如图16、17所示。

由图16、17可以看出：(1)在模型运动初始阶段，推靠销钉x方向的加速度出现浮动且持续时间较长，y方向的运动参数曲线较为光滑。(2)相较于理论曲线(图7)，推靠销钉运动参数的变化规律和总体趋势与理论值基本一致，验证了推靠销钉运动理论结果的正确性。(3)与推靠杆端口y方向运动曲线(图15)相比，两者在y方向有相似的运动趋势及规律。

图15 推靠杆端口y方向运动曲线

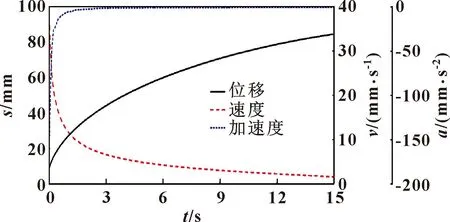
图17 推靠销钉y方向运动曲线

幅角φ1和φ3的运动曲线，如图18、19所示。

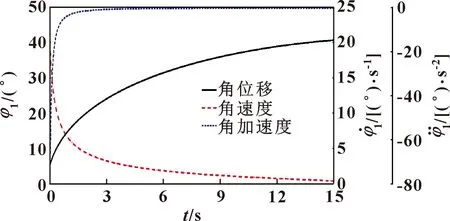
图18 幅角φ1仿真运动曲线

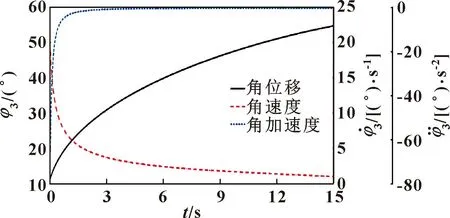
图19 幅角φ3仿真运动曲线

由图18和19可以看出：(1)幅角φ1和φ3的运动曲线不仅有相似的运动规律，而且与推靠杆端口和推靠销钉y方向运动参数有相似的运动趋势。(2)与幅角φ1和φ3的理论曲线(图8、9)相比，两者的运动参数变化规律和总体趋势与理论值基本一致，验证了推靠系统幅角φ1和φ3运动理论求解过程的正确性。

上述推靠杆端口和推靠销钉沿坐标轴方向的加速度分量与理论值对比，均在仿真模型最初运动阶段发生范围性变化，不如理论曲线平滑。分析造成这样结果的原因如下：

(1)在理论分析阶段，运用一些数学理论进行公式推导，没有考虑物体之间的相互作用以及实际的约束条件；而ADAMS仿真过程中，建立的约束和运动副接近于真实工况。比如分析大小丝杠驱动的运动状态，理论分析简单地用vA和vB进行表示，ADAMS仿真则添加螺旋副建立丝杠与大小丝杠驱动之间的联系，后者更接近真实工况。

(2)理论分析推导的公式是随时间变化的离散型数据，每一个时刻对应一个值，前后时刻的结果互不影响，而仿真模拟是连续的过程，软件通过自带的内置函数经过多次迭代计算结果[13]，比如，仿真时取相同的仿真时间，不同的分析步数，得到的结果之间都会有差异。因此，加速度曲线在运动前期，仿真与理论会有所差别，但最终的运动参数和趋势是一致的。

4.2 测量性能分析

在实际测井作业过程中，井径测井仪的测量性能是评判其结构设计合理性的重要依据。为了证明所设计的双向驱动井径测井仪具有良好的测量性能，本文作者将进一步建立双向驱动井径测井仪推靠系统测量仿真模型，对其测量性能进行研究。

4.2.1 建立模型

在测井仪推靠系统运动仿真模型(图13)的基础上，增加模拟井壁，推靠臂与推靠杆之间使用软弹簧连接并添加移动副，推靠杆与井壁之间创建实体接触，支撑杆与地面之间添加移动副并建立驱动(10.0×time)，模拟测井仪被匀速提升，其余连接均为固定连接[14]，完成测井仪推靠系统测量仿真模型的建立。

测井仪推靠系统测量仿真模型如图20所示。

图20 测井仪推靠系统测量仿真模型

4.2.2 仿真分析

设置仿真终止时间为45 s，仿真步数为400。

推靠杆端口上下端轨迹曲线如图21所示。可以看出：推靠杆端口上、下端轨迹曲线平滑，表明测井仪可将井壁的凹陷和凸起转化为曲线的波峰和波谷，直观表示井壁的凹凸程度，具有良好的测量性能。

图21 推靠杆端口上(a)、下(b)端轨迹

测井仪在测量井径轨迹作业时，弹簧弹力与井壁接触力随井径大小变化而变化，其变化情况可以体现出测井仪结构的动态稳定性[15]，只有在正常范围内变化，测量数据才具有更高的可信度和参考价值，弹簧弹力和接触力曲线图，如图22、23所示。

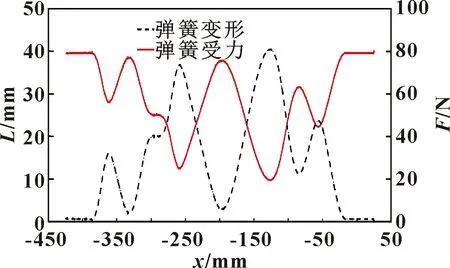
图22 弹簧弹力曲线

由图22可以看出：(1)预压弹力为80 N，弹簧的伸缩量与推靠杆端口的径向位移(轨迹)成线性关系。(2)在测量过程中，弹簧始终没有超出最大伸缩值(40 mm)，保证了测量数据的可靠性并为推靠杆端口和井壁的紧密贴合提供保障。

由图23可以看出：(1)接触力曲线不光滑，随推靠杆端口径向位移(y方向)增加而减少。(2)在推靠杆端口径向位移减少时，接触力发生突变(波峰凸起)，随着位移减少斜率的增大，接触力凸起程度越明显。

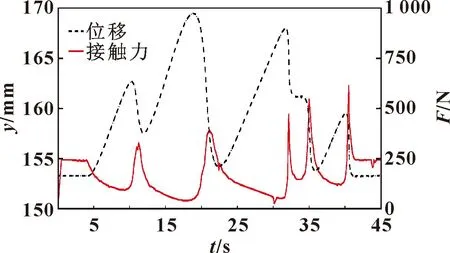
图23 接触力曲线

由此可见在测井作业时，接触力随着井径的变化而变化，其变化规律符合真实情况。

5 结论

(1)建立了新型井径测井仪物理结构模型，相比传统井径测井仪，此模型具有多动力源、双向丝杠驱动、分动式协作和测量性能稳定等优点。

(2)运用复数矢量法推导出推靠系统的运动参数理论计算公式，确定了其运动变化规律，得出y方向位移(点C′)与vA和vB之和之间存在正相关关系，证明了双向丝杠驱动比单向丝杠驱动具有更多的速度组合且减少了初始运动冲击，提高了传动稳定性，为后续推靠系统运动学分析奠定了基础。

(3)通过ADAMS虚拟仿真对测井仪推靠系统运动性能和测量性能进行分析，将仿真与理论分析结果进行对比，推靠杆端口和推靠销钉的运动曲线具有较高的吻合度，验证了理论分析模型的合理性与正确性；测量性能仿真诠释了双向驱动井径测井仪可精确测量出凹凸井壁的轨迹曲线，具有良好的测量性能，为井径测井仪的实际应用提供理论依据。