蛇形空间机械臂单个2-DOF关节的运动学标定

2024-03-14宋国庆赵成浩袁俊杰张忠海何广平

机床与液压 2024年3期

宋国庆，赵成浩，袁俊杰，张忠海，何广平

(1.北方工业大学机械与材料工程学院，北京 100144；2.北京航天测控技术有限公司，北京 100041)

0 前言

近年来，超冗余蛇形空间机器人具有高度的可操作性、灵活性和良好的动力学性能，在学术界和工业界引起了极大的兴趣。比较传统机器人，超冗余蛇形空间机器人具有众多的自由度，能够在狭小的空间中灵巧操作。因此，它们在检测、维护、维修和救援等任务中拥有巨大的潜力，如核工业[1]、航空发动机维修[2]、空间站维护维修[3]、地震救援[4-5]等。

精度是描述机器人工作性能的关键性指标，随着高价值基础设施对高精度检测需求的日益增长，对蛇形空间机械臂的末端位置精度提出了更高的要求。近年来，国内外的专家和学者针对这一问题分别从结构设计[6-7]、运动学模型[8]、动力学模型[9-10]、控制系统设计[11]和轨迹规划[12-14]等方面进行了分析，虽然已有大量提高蛇形臂末端定位精度的研究，但关于原始误差对于蛇形臂精度影响的文献较少。LIN等[15]针对这一问题，分析了蛇形臂关节平面绳索孔的位置误差和绳索长度误差对蛇形臂末端位置精度的影响，但是并未指出其余结构参数的误差对于末端执行器精度的影响。从这一问题出发，蛇形空间机械臂的末端位置精度可以通过运动学标定进行提高，一般来讲可以分为以下4步[16]：(1)针对研究目标，建立包含所有误差源的误差模型；(2)通过灵敏度分析，辨识出对机器人末端执行器影响较大的误差源；(3)利用内部传感器或外部测量装置对机器人的末端位姿进行测量；(4)运用误差辨识原理，对机器人的控制模型进行修正。

蛇形空间机器人的单个2-DOF关节为柔性绳索驱动的并联机构。在并联机构的误差分析中，误差建模是误差分析和运动学标定的基础，通常来说，误差建模方法分为以下3种：(1)矩阵全微分理论[17-18]；(2)闭环矢量法[19-20]；(3)旋量理论[21]。然后，对已建立好的误差模型进行灵敏度分析，蒙特卡洛法[22]和灵敏度系数法[23]是两种常用的方法。比较蒙特卡洛法，灵敏度系数法具有更加清晰的数学意义，能够在统计意义上反映出蛇形臂结构误差的标准差对于末端精度的影响[24]，为机械加工的公差设计提供理论指导。最后，通过运动学标定[25-27]，对控制器中的名义运动学模型进行修正。

上述文献表明，在大多数关于并联机器人误差分析的研究中，研究的对象通常是基于刚性关节驱动的具有确定输入的并联机器人。对于蛇形空间机械臂这一类柔性绳索驱动的具有超确定输入的串/并联机器人的研究中，由于约束的存在，其精度分析问题变得较为复杂。本文作者以提高柔性绳索驱动的蛇形空间机械臂末端位置精度为目标，对单个2-DOF关节进行分析。首先，通过矩阵全微分理论建立2-DOF关节的误差模型，并在此基础上，依据全局灵敏度指标指导机械臂的加工和装配；最后，通过正则化的方法对2-DOF关节进行运动学标定，进一步提高机械臂的末端位置精度。

1 蛇形臂空间机器人介绍

蛇形臂空间机器人具有22个自由度，包括直线导轨滑台1个自由度、末端执行器1个自由度，机械臂由10个模块化2-DOF关节串联，共20个自由度。蛇形臂机器人三维模型如图1所示。由绳索驱动机械臂关节运动，控制器和驱动器被放置在机器人的上部，绳索穿过圆盘和带有绳索导向管道的绳索导向部件，进入驱动系统。绳索导向部件整体为3D增材制造技术加工制作，通过法兰连接到机械臂。末端执行器具有360°旋转功能和快装接口，可安装夹爪等模块化工具集。为提高机器人的负载能力和末端执行器的精度，机器人关节的直径/长度的比例设计得尽可能大[28]。且根部关节为耦合驱动，头部关节为解耦合驱动，通过宏/微操作策略，可以对机械臂的末端位置误差进行补偿。

图1 蛇形臂机器人三维模型

机械臂由结构完全相同的模块化关节组成，为提高机械臂的位置精度，不失一般性，对机械臂单个2-DOF关节进行分析。图2(a)展示了单个关节的虚拟样机。共有驱动绳索运动的3个输入自由度和2个输出自由度，驱动方式为冗余驱动。模型可简化为图2(b)所示的机构简图，该2-DOF关节由1个静平台、1个动平台、1个万向节、1根连杆以及3根结构和性能完全相同的绳索组成。Ai为绳索与静平台的交点，绳索的末端点Bi连接到动平台，3根绳索与动(静)平台的连接处呈120°均匀分布，O1分别被投影到动、静平台的点O0和点O2处，O0和O2分别为动、静平台的圆心。为了更好地描述2-DOF关节的运动关系，以静平台点O0建立全局坐标系O0-x0y0z0，z0轴方向竖直向上，x0轴指向A1，y0轴由右手定则确定。类似地，以点O2为圆心建立动平台的坐标系O2-x2y2z2，z2垂直于动平台竖直向上，x2指向点B1，y2的方向由右手定则确立。将O2-x2y2z2坐标系向上平移至点O′，即可得到坐标系O′-x′y′z′。

图2 蛇形臂单个2-DOF关节

(1)2-DOF关节逆向运动学

对蛇形臂机器人2-DOF关节进行分析，机械臂的逆运动学分别包含操作空间至位形空间和位形空间至驱动空间的两重映射关系。以万向节十字交叉轴中心点O1为原点，建立坐标系O1-x1y1z1，x1轴平行于x0轴，y1轴平行于y2轴，z1轴与h2共线，则O0到O1、O1到O′的坐标变换关系可以表示为

O0TO1=T(0,0,h1)R(Y,β)

O1TO′=R(X,α)T(0,0,h2+h3)

(1)

T()和R()分别表示平移和旋转齐次变换矩阵。则点O0到点O′的齐次坐标变换矩阵可以表示为

O0TO′=O0TO1O1TO′

(2)

设cα=cosα、sα=sinα、sβ=sinβ，则2-DOF关节动平台点O′在全局坐标系中的坐标可以表示为

PO′=[(h2+h3)cαsβ,-(h2+h3)sα,h1+(h2+h3)cαcβ]T

(3)

由于2-DOF蛇形机器人关节的驱动方式为冗余驱动，且x、y、z坐标具有耦合性，由式(3)可知，当末端执行器位置坐标已知时，取x坐标和y坐标可以反解得到关节角α和β。

(4)

绳索的长度只在单个关节的动平台和静平台之间发生变化，而连杆内部的绳索长度保持不变。因此，驱动空间到位形空间的运动学仅涉及单个关节动、静平台之间的区域。根据各点之间的映射关系，可以求得点O0到点O2的齐次变换为

(5)

绳索孔在基坐标系O0-x0y0z0中的位置坐标可以表示为

ai=(rcφi，rsφi，0，1)

(6)

绳索孔在动坐标系O2-x2y2z2中的位置坐标可以表示为

bi=(rcφi，rsφi，0，1)

(7)

其中：r为动/静平台3个绳索孔距离中心点的距离；φi(i=1,2,3)表示动/静平台上的第i个绳索孔和中心点连接线分别与x0和x2轴之间的夹角，呈120°均匀分布。故第i根绳索的长度为

(8)

联立式(4)和式(8)，可以得到蛇形机器人驱动空间到工作空间单个关节的运动学逆解。

(2)2-DOF关节正向运动学

由于单个2-DOF关节为冗余驱动的并联机构，其正向运动学较难求解，且由式(8)可知，绳索长度到末端执行器位置坐标的映射关系为非线性关系，通过数值优化的方法进行迭代求解。根据式(8)建立的数学模型，优化模型的目标函数可以表示为

(9)

其中：Li(Θ)由式(8)确定，Θ=(α，β)为优化变量。对于给定任意一组绳索长度l1、l2、l3，可通过数值迭代的方法，近似求解对应的2-DOF关节角变量Θ。文中基于梯度法进行求解，其迭代公式可以表示为

Θk+1=Θk+αkpk

(10)

其中：Θk为第k次迭代的优化变量值；αk表示优化步长；pk表示优化方向。基于梯度法求解末端姿态，优化方向为负梯度方向，即

(11)

对于式(9)表示的非线性二次型目标函数，利用Wolfe条件确定优化步长αk时，通常需要进行多次迭代，以选择适当的步长系数αk。采用如下自适应机制

(12)

其中：1.2和0.2为变步长系数。通过以上的优化迭代算法，能够对驱动空间到位形空间的正运动学进行求解。联立式(3)，完成整个正向运动学的迭代求解。

2 蛇形臂2-DOF关节误差分析

2.1 误差建模

绳索驱动的单个2-DOF关节的运动学建模涉及多个空间的映射关系，且驱动方式的冗余特点给机械臂误差模型分析带来较大困难。对单个关节进行误差建模，模型可简化为包含所有误差源的2-DOF关节，示意图如图3所示。根据动平台和静平台之间的运动学映射，驱动空间到位形空间的逆运动学模型可以重建为

图3 蛇形臂2-DOF关节几何结构误差示意

li=[(ri,1cφi,1cβ-ri,2cφi,2+h2cαsβ+ri,1sφi,1sαsβ)2+(ri,1sφi,1cα-h2sα-r2sφi,2)2+(h1-ri,1cφi,1sβ+h2cαcβ+ri,1sφi,1cβsα)2]1/2

(13)

联立式(4)和式(13)，可以得到该2-DOF关节驱动空间到工作空间的逆运动学模型，将其简写为

fi(ri，1，ri，2，h1，h2，h3，φi，1，φi，2，x，y，li)=0

(14)

其中：ri，1、ri，2、h1、h2、h3、φi，1、φi，2均为已知的结构参数；li为输入参数；x、y为2-DOF关节末端执行器的输出位置参数。对式(14)的所有变量进行微分得

(15)

其中：Pj(j=1，2)为2-DOF关节的位置坐标x和y；qk(k=1，2，…，18)为不包含末端位置的18个结构参数。联立式(14)和式(15)，将误差模型整理成矩阵形式，可以表示为

Jadea=Jmdqm

(16)

整理式(16)，并用结构误差和末端执行器位置误差的有限小量Δqm和Δea分别替换dqm和dea，可以得到Δqm和Δea之间的映射关系。

Δea=JeΔqm

(17)

2.2 误差模型验证

为了验证结构误差模型的正确性，提出一种误差模型的验证方法。该方法对已经建立的正确的运动学模型，引入几何参数误差Δqm(m=1,2,…,18)，计算末端执行器的位置偏移量，与该结构误差Δqm在误差模型中计算得到的末端位置误差进行比较，若结果相同，则误差模型正确；反之，则误差模型错误。几何误差模型验证流程如图4所示。

图4 几何误差模型验证流程

具体步骤为：

(1)从表1中随机选取2-DOF关节的任一位置，位置的选取要符合2-DOF关节工作空间的要求。

表1 工作空间内的末端位置

(2)从表2中选择任一给定误差，为了更直观体现几何结构误差对于末端姿态的影响，误差大小的选取是随机的且通常要比设计误差大一些。

表2 给定2-DOF关节的几何误差参数

(3)联立式(4)和式(8)，计算驱动绳索的长度li。

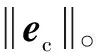
(5)计算在该位置下的误差影响系数矩阵Je。

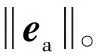
(7)比较步骤(4)和步骤(6)的计算结果。

(8)返回步骤(2)，选择另一误差重复以上步骤。

(9)返回步骤(1)，选择另一位置重复以上步骤。

图5 误差模型与运动学模型求解误差对照

3 蛇形臂2-DOF关节误差灵敏度分析

3.1 误差灵敏度指标

基于建立的误差映射模型对结构误差进行灵敏度分析，能够评估所有结构误差对于末端姿态的影响程度的大小。此节在统计意义上，定义了能够评价各个结构误差对于动平台位置误差影响的灵敏度指标。假定结构误差服从均值为零的正态分布，可以建立单个2-DOF关节的误差模型为

(18)

式中：Δqm，i表示单个2-DOF关节第i条支链Δqm中的第m个元素；Je，i，m为系数矩阵Je中第i行第m列元素。则Δea的标准差可以表示为

(19)

其中：σ(Δea)可以表示由单位标准差Δqm引起的单位标准差Δea的偏离程度，因此，可以定义ωm为Δea的局部灵敏度。

(20)

由于Je，i，m与位置坐标有关，为了评价各个结构误差对于指定工作空间的敏感程度，定义Je，i，k在指定工作空间V中的均值um为全局灵敏度，作为评估Δqm，k对于末端位置精度的影响系数。

(21)

3.2 误差灵敏度分析

基于式(20)和式(21)建立的误差灵敏度模型，对蛇形臂单个2-DOF关节进行灵敏度分析，机械臂的关键设计参数如表3所示，根据蛇形空间机械臂的设计要求，单个2-DOF关节对应的x、y的工作空间为(-24，24) mm。

表3 2-DOF关节主要设计参数

计算结果如图6所示。可知：末端定位精度对于关节长度h1最为敏感，其次是绳索长度l1、l2、l3和关节长度h2、h3，绳索孔的角度φi，j对于2-DOF机械臂的影响最小。因此在设计和装配阶段，应重点保障关节长度的设计和装配误差，其次应注意绳索孔位置误差对于末端精度的影响，绳索的长度可以通过控制进行补偿。因此，在公差设计时，如果已知Δqm引起的Δea的标准差大小，则可以计算出Δqm的公差。例如，如果由σ(Δea)引起的末端执行器误差被限制在26 μm，那么静平台的关节长度h1的公差应在±(3×26/1.477) μm范围内，也就是±52.81 μm，依次可以计算出所有几何参数的公差大小。

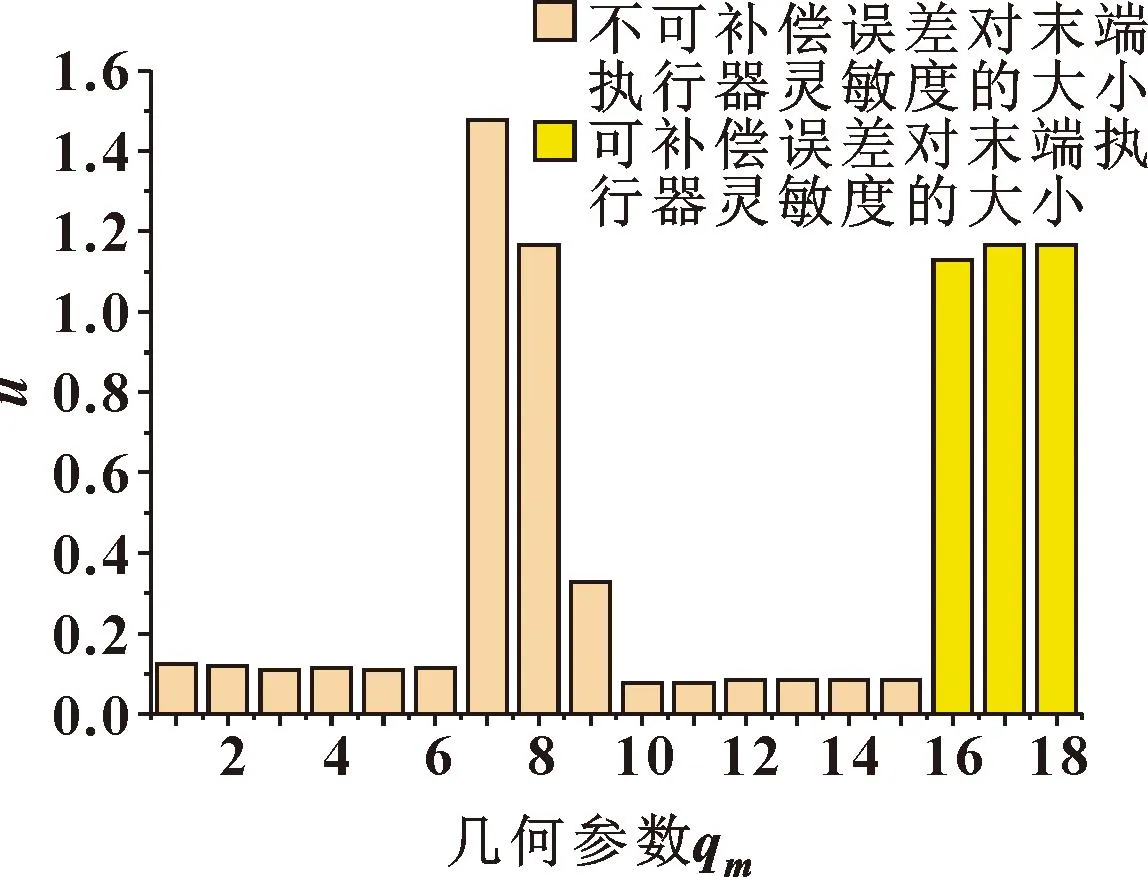
图6 灵敏度条形图

4 蛇形臂2-DOF关节运动学标定

由于存在运动学误差，导致末端执行器的实际运动与名义运动有所不同。在此节中，提出一种正则化的参数辨识方法，通过最小二乘法进行数值迭代，获得结构参数的几何误差，通过误差辨识，补偿和修正控制器中的名义运动学模型。

4.1 误差辨识原理

根据式(17)可知，对18个结构误差进行辨识，至少需要9组末端执行器的位置坐标，误差模型可以表示为

(22)

(23)

其中：I为单位矩阵；α为正则化参数，可通过广义交叉验证(GCV)和遗传算法(GA)进行求解。由于式(23)为非线性函数，难以得到解析解，因此，可以采用Gauss-Newton数值迭代进行求解，具体流程如图7所示。目标函数为

(24)

图7 数值迭代法求解几何误差

其中：(Xm，i，Ym，i)为第i组末端位置的测量值。通过对名义尺寸进行迭代修正，逐渐逼近真实加工尺寸，则数值迭代方法可以表示为

德国罗森伯格，一家拥有60年历史的、拥有顶尖技术优势的无线射频和光通信技术制造商，其在移动通信、汽车电子、测试计量以及光传输等领域以领先的技术优势、先进的生产工艺和严苛的品质保证而享誉世界。罗森伯格FAKRA®、HSD®的信号传输技术作为行业标准被殴美日系全线车型上广泛采用；在HVR®高电压和大电流的传送技术上具有屏蔽性好、稳定性高的技术优势；全新MTD®技术，完美诠释了车载以太网解决方案。

(25)

4.2 数值仿真

图8 运动学标定仿真流程

表4 理想末端位置和标定前后的末端位置单位：mm Tab.4 Ideal end positions and end positions before and after calibrations Unit：mm

图9 运动学标定前、后位置误差曲线

图10 运动学标定实验装置

5 实验

在此节中，提出一种适用于蛇形空间机械臂的单个2-DOF关节的运动学标定方法[29]，进一步验证标定算法的有效性。如图 10所示，通过在关节末端安装激光发射器，对末端发射的激光点的位置进行采集和处理，得到末端位置坐标。与理想末端位置坐标进行对比，能够得到机器人的末端位置误差。该方法不需要对基准进行标定，具有节约时间、成本低、计算简单和易于实现的特点。

(1)在2-DOF关节的末端安装激光发射器，确保激光发射器位于末端关节的中心位置且与动平台保持竖直。

(2)在2-DOF关节的正上方水平放置网格板，用于接收激光笔发射的激光信号，并通过几何方法对末端执行器的位置信息进行放大。

(3)经过相机采集放大后的末端位置信息，并通过ScanIt软件对坐标点的位置进行提取。通过几何计算机械臂的末端位置坐标。网格板的误差为0.1 mm，末端执行器的测量误差为0.012 mm。

随机生成20组末端位置，对运动学标定算法进行验证，运动学标定的实验结果如图 11所示。运动学标定实验结果与仿真结果相似，从图11可以看出：经过运动学标定后的最大误差由2.19 mm降低至1.12 mm，末端位置精度得到明显提高。在随机选取的20组末端姿态中，标定前x方向和y方向的平均误差为0.23 mm和1.67 mm，标定后的平均误差为0.02 mm和0.3 mm，末端位置精度得到显著提高，证明所提出的运动学标定算法是有效的。考虑到绳索只能受拉的特点和绳索弹性变形的影响，末端的位置误差可以通过进一步调节绳索的拉力进行调整。