基于变密度法深孔钻床主轴箱可靠性拓扑优化
2024-03-14胡韶岩薄瑞峰刘韶轩陈振亚
胡韶岩,薄瑞峰,刘韶轩,陈振亚
(中北大学机械工程学院,山西太原 030051)
0 前言
应力约束下的连续体拓扑优化是近几十年的研究热点[1-3]。孟庆轩等[4]基于各向同性材料惩罚模型,建立了以应力为约束的热固耦合连续体结构拓扑优化模型。EMMENDOERFER 和FANCELLO[5]提出一种基于水平集的方法来解决局部应力约束下质量最小化的结构拓扑优化问题。一般而言,上述应力约束下的拓扑优化在假设所有参数都是确定性时表现良好,但在实际工程结构的制造和使用阶段存在大量不可避免的不确定因素,包括材料性能、结构几何尺寸以及外部载荷等的变化。在这种情况下,研究具有不确定参数的拓扑优化具有十分重要的意义。
多年来,已经提出了将不确定性纳入设计优化过程的不同方法,其中最流行的不确定方法是基于可靠性拓扑优化(Reliability-Based Topology Optimization,RBTO)方法。周松等人[6]对自卸车翻转轴进行可靠性拓扑优化,在满足可靠性的条件下减轻了质量。刘国梁等[7]基于不确定理论提出了以可靠性为求解策略的拓扑优化。虽然大量学者对不确定性设计、可靠性校核和拓扑优化等各个方面都有着深入的前期研究[8],但关于深孔机床关键结构件的可靠性拓扑优化的研究还比较少。
主轴箱作为深孔机床的关键件,其强度、刚度及动态特性对机床的加工精度有很大的影响,特别是在高速切削场合,主轴箱的动态特性直接影响到机床的加工精度[9]。本文作者以TBT-ML500深孔钻床主轴箱为研究对象,提出一种基于变密度法的可靠性拓扑优化方法,目的是寻找在载荷和材料不确定性下满足应力约束和位移约束的最小质量结构。用一阶可靠性方法和Roenblatt逆变换将可靠性拓扑优化解耦为两个步骤,即确定性分析和可靠性分析。
1 可靠性拓扑优化
1.1 可靠性拓扑优化问题描述
在传统的结构拓扑优化中,不确定性是通过使用安全系数来考虑的。然而,安全系数法在许多情况下会受到限制,导致设计过于保守或不安全。
因为可靠性拓扑优化与确定性拓扑优化有相同的优化目标,作者研究的可靠性拓扑优化与确定性拓扑优化的唯一不同点在于它们的约束。与确定性拓扑优化相比,可靠性拓扑优化采用概率约束来确保拓扑优化结果同时满足稳定性、可靠性和经济性。
可靠性拓扑优化的目标函数是质量最小化,将位移和应力作为优化问题的约束条件,设计变量是每个有限元中的函数密度ρ。将弹性模量和载荷当作不确定变量,并且假设两个不确定变量服从正态分布。
1.2 可靠性拓扑优化的数学模型
基于可靠性拓扑优化问题变量界定,具有应力约束和位移约束的连续体拓扑优化在数学上的表达如下:
(1)
式中:ρ为密度向量;V为结构体积向量;ρi和Vi分别为第i个元素密度和体积;x为随机变量向量;σVM为von Mises等效应力;σlim为材料的强度极限;uj为第j个节点位移;ulim为阈值;N为设计区域单元总数;Nc为约束总数;Pt为允许的失效概率;Pfi是由下式给出的失效概率。
Pfi(ρ,x)≤P(gi(ρ,x)>0)
(2)
式中:gi是极限状态函数,gi>0表示被分析系统的故障;P表示给定事件发生的概率。
1.3 解耦格式
从式(1)中注意到在针对设计变量的结构优化中嵌套了随机变量的可靠性分析。直接求解嵌套优化问题会导致非常苛刻的计算例程和收敛困难,并且在大多数情况下不是有效的方法。出于这个原因,本文作者采用一阶可靠性方法提出了可靠性拓扑优化-解耦格式,因为它灵活且易于与现有的确定性优化算法一起使用。
极限状态gi的可靠性指标可以定义为
(3)
式中:βi为结构第i个极限状态的可靠性指标;βt为其相应的目标许用可靠性指标,由下式给出:
βt=Φ-1(1-Pt)
(4)
如果故障概率已知或使用某种近似方案,则可以准确评估该可靠性指标。许多近似方法和模拟方法被用于这类问题,包括一阶可靠性方法(FORM)、二阶可靠性方法(SORM)、抽样方法如蒙特卡罗模拟(MCS)和重要抽样等。其中一阶可靠性方法被认为是最有效的计算方法之一,也是最常用的可靠性方法。在使用一阶可靠性方法的情况下,精确的可靠性指标由Hasofer-Lind可靠性指标近似求解[10]。
根据一阶可靠性方法,概率约束可转化为可靠度指标约束:
Pfi≤Pt⟹βi≥βt
(5)
其中,结构可靠性指标相对于不确定变量的灵敏度由下式求得:
(6)
以Hasofer-Lind可靠性指数近似求得的最优解μ*为设计点。根据Roenblatt逆变换[11],获得随机变量的修正值:
(7)
式中:ηxi和σxi分别是正态随机变量xi的均值和方差。
对上式中的目标函数相对于不确定变量参数的灵敏度通过有限差分法计算:
(8)
根据式(9)解出对应的不确定变量的修正值,可将可靠性拓扑优化转化为等价的确定性拓扑优化,即可靠性拓扑优化-解耦格式的数学模型如下式所示:
(9)
2 机床主轴箱算例分析
以TBT-ML500深孔钻床主轴箱为例,在弹性模量和载荷变化不确定的情况下,用可靠性拓扑优化-解耦格式对主轴箱进行轻量化设计,具体计算流程如图1所示。主轴箱底座与机床通过螺栓连接,因此将主轴箱的6个螺栓孔处设置为固定约束。深孔机床主轴箱主要受到机床工作时产生的钻削力和自身重力。如图2(a)所示,红色B处为施加的载荷,黄色C为设置的主轴箱自身重力。定义主轴箱的材料为TH200,取材料的弹性模量E=1.4×105MPa,泊松比0.28,密度7 800 kg/m3[12]。根据机械加工工艺手册[13],主轴箱载荷即钻削力F,由下式给出:
(10)
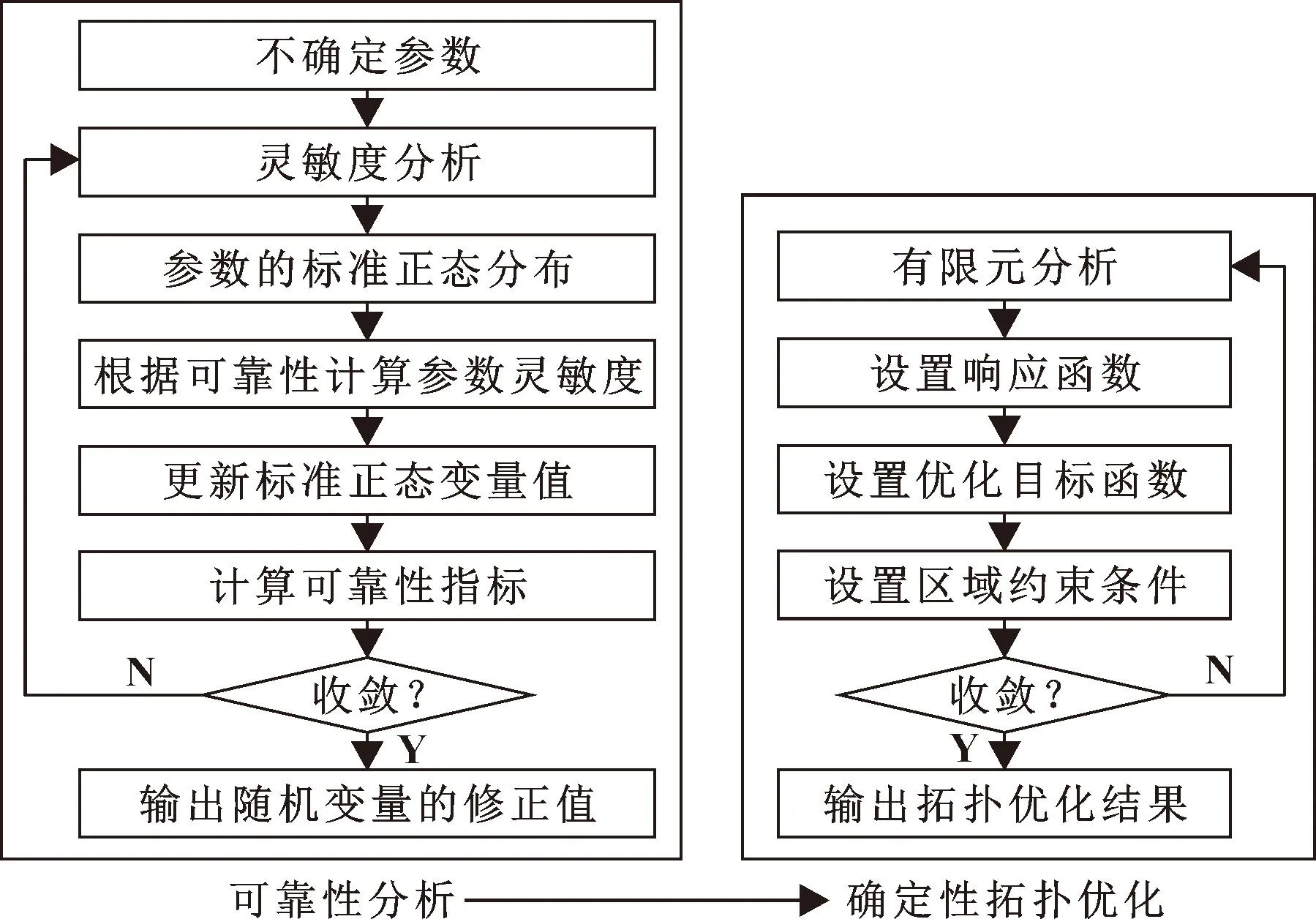
图1 计算流程
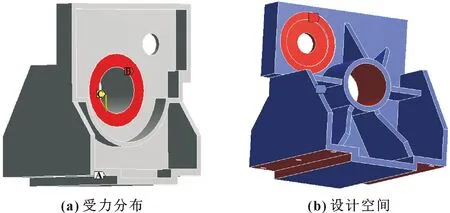
图2 主轴箱受力分布和设计空间
式中:PF=410,NF=1,EF=0.7,MF=1。
将非设计区间设置为主轴孔、安装电机的孔以及底座的安装固定区域,如图2(b)红色部分所示;其余部分设置为优化区域,如图2(b)蓝色部分所示。将制造工艺约束设置为最小成员尺寸约束,即25 mm,拓扑构型密度阈值设置为0.2。
在拓扑优化过程中,当将所有参数都视为确定性时,拓扑优化的最终结果具有大约41.8%的体积分数,得到的最佳拓扑构型如图3所示。当将弹性模量、钻削力看作是满足正态分布的不确定性变量时,并将可靠性指标约束β*设置为3、4、5,设置标准差σ=0.1m,m为随机变量的均值。在β*=3的情况下,拓扑优化的最终结果具有大约55.1%的体积分数,最佳拓扑构型如图4(a)所示。图4(b)和(c)分别是β*=4和β*=5的最佳拓扑构型,拓扑优化的最终结果分别为63.6%和65.5%的体积分数。不确定变量的修正值和拓扑优化结果汇总于表1。
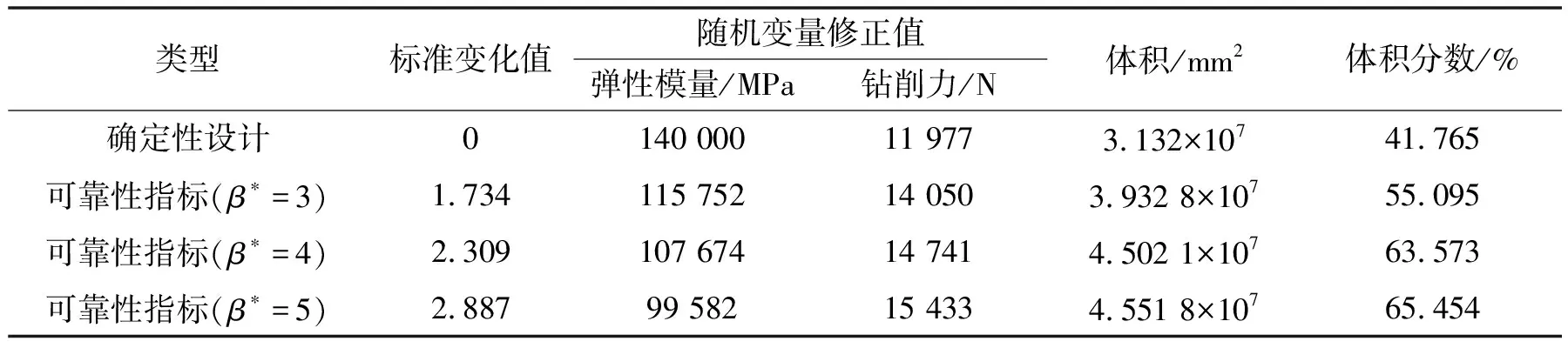
表1 优化设计结果

图3 确定性拓扑优化
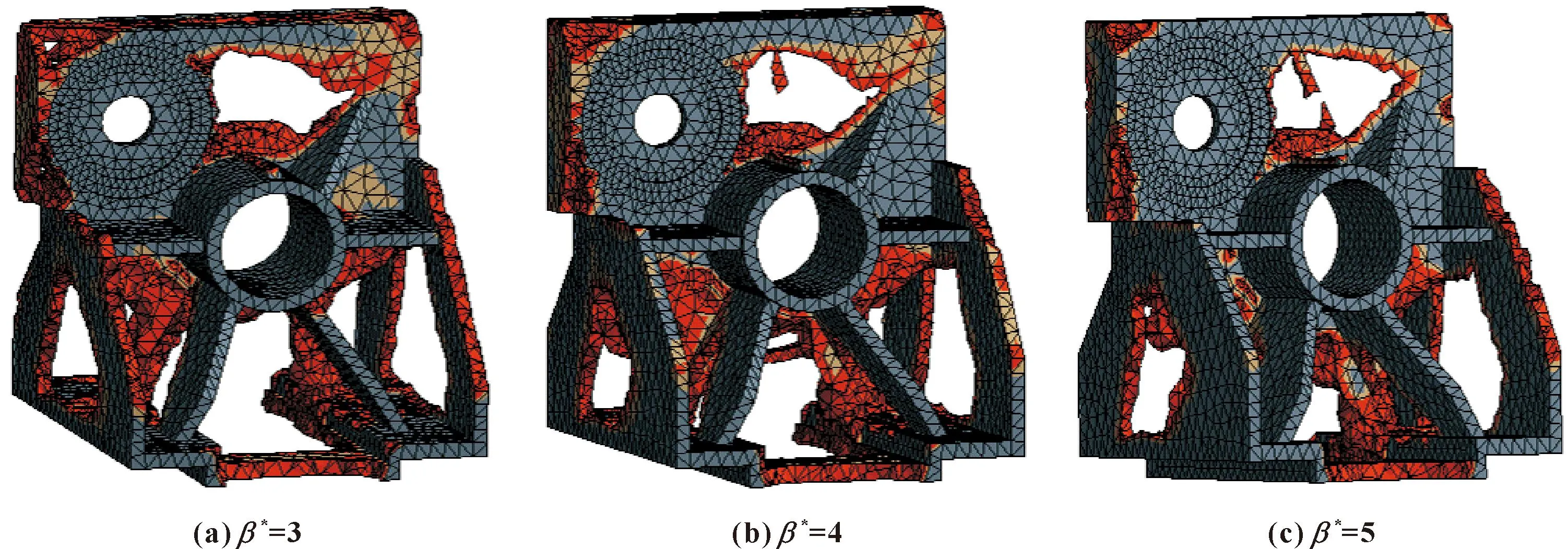
图4 可靠性设计
由图3和图4可以看出:确定性拓扑优化的最佳拓扑构型和具有不同可靠性指标的可靠性拓扑优化的最佳拓扑构型之间有很大的差异。从表1可以观察到,与确定性拓扑优化相比,可靠性拓扑优化所保留的材料体积分数明显增大,并且随着可靠性指标增大而增大。这是因为随着可靠性指标的提高,修正的数值变化变大,需要更多的材料来提高机构的安全性。
为了验证可靠性拓扑优化的结果优于确定性拓扑优化,考虑制造工艺条件、材料分布情况和设计准则,对确定性拓扑优化后的模型和可靠性(β*=5)拓扑优化后的模型进行修复,修复后的模型如图5所示。
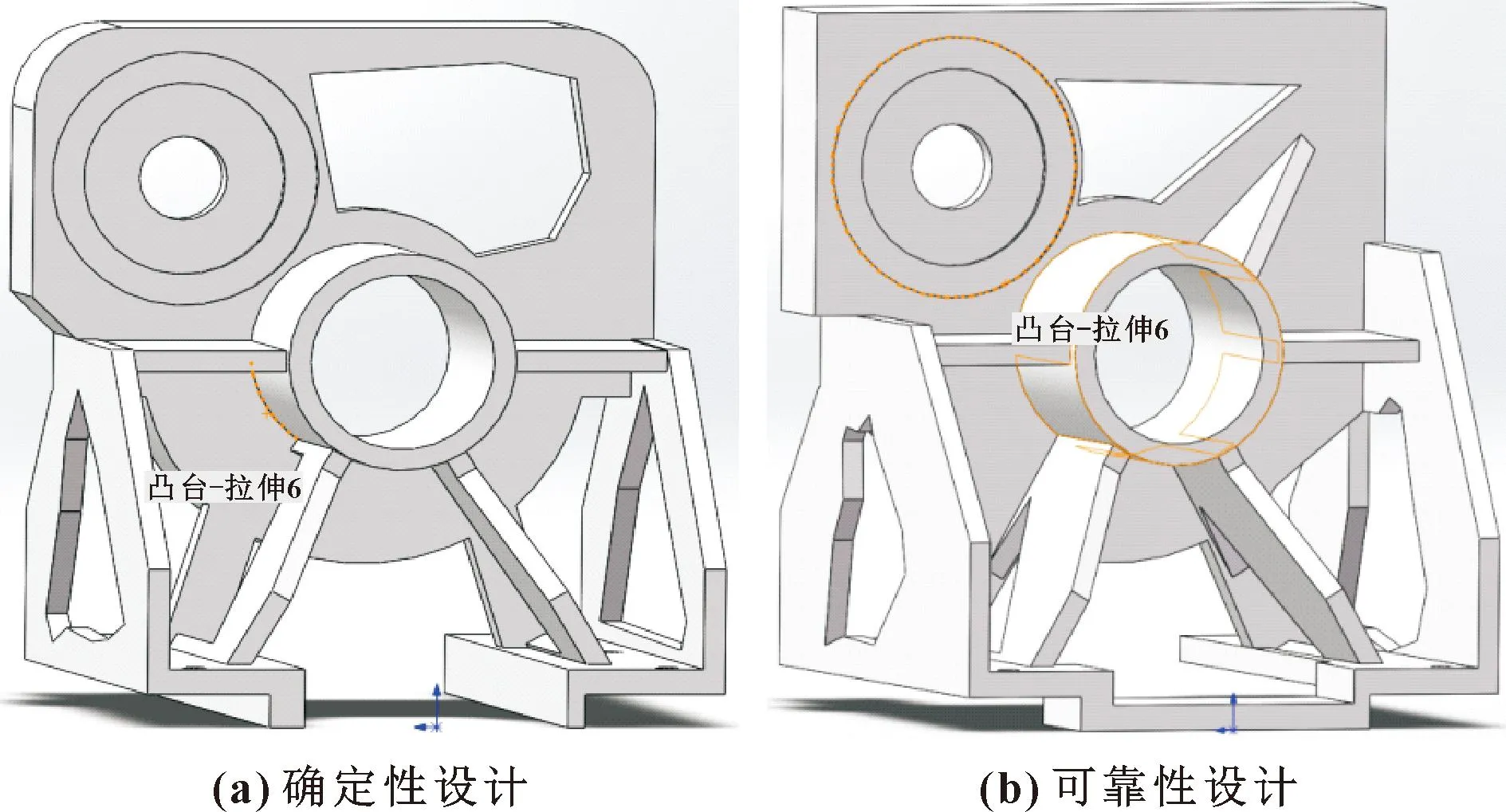
图5 修复模型
依据最终设计方案,分别对确定性拓扑优化和可靠性拓扑优化修复后的主轴箱结构进行有限元分析,有限元分析结果如图6所示,主轴箱优化前后各项性能指标对比如表2所示。从表2可以看出:确定拓扑优化后的最大变形量增大了19.58%,最大应力增加了15.43%,质量减少了36.45%;可靠性拓扑优化后的最大变形量较少了0.4%,最大应力增加了13.13%,质量减少了29.68%。从以上数据可以得到:尽管可靠性拓扑优化后的质量比确定性拓扑优化有一定程度上的增加,但是,最大应力和最大变形都有所减小。这意味着随着可靠性要求的提高,结构的应力和变形减小。并且与确定性拓扑优化相比,可靠性拓扑优化材料分布均匀,具备良好的可制造加工性,结果更趋于合理。因此,在设计阶段考虑不确定因素对于满足实际应用中的安全要求极其重要。
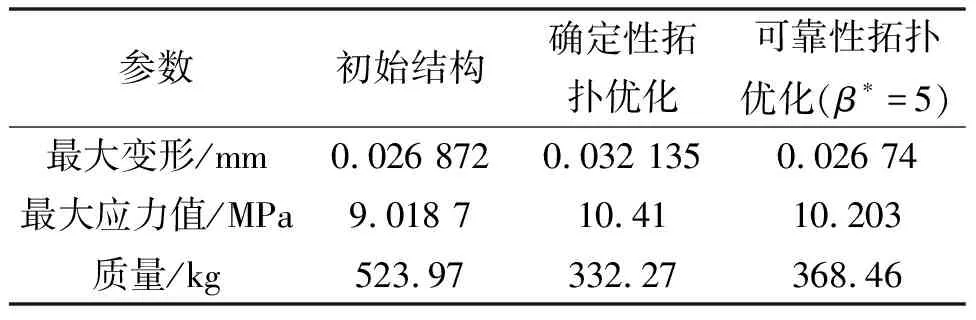
表2 主轴箱优化前后各项性能指标

图6 修复模型有限元分析结果
3 结论
针对弹性模量和载荷变化带来的不确定性,建立了应力和位移约束的可靠性拓扑优化模型,目的是在满足可靠性和稳定性要求的前提下,使质量最小。然后采用一阶可靠性方法进行可靠性分析,以保证算法的稳健性和有效性。最后通过对TBT-ML500深孔钻床主轴箱进行可靠性拓扑优化,既验证了此方法的有效性又实现了轻量化。结果表明,可靠性拓扑优化的最优拓扑结构与确定性拓扑优化有很大差异,这说明在拓扑优化中考虑不确定性影响的必要性。更严格的安全要求不可避免地导致更低的经济设计。
