足式机器人腿部关节改进单神经网络PID控制算法研究
2024-03-14马程蒋刚郝兴安蒲虹云陈清平黄建军徐文刚黄璜
马程,蒋刚,郝兴安,蒲虹云,陈清平,黄建军,徐文刚,黄璜
(1.成都理工大学核技术与自动化工程学院,四川成都 610059;2.成都理工大学机电工程学院,四川成都 610059;3.成都陵川特种工业有限责任公司,四川成都 610110)
0 前言
机器人技术自20世纪60年代问世以来,在人类科学技术不断发展中机器人技术也在飞速发展,目前机器人技术被广泛运用于工业和军事领域,因此研究机器人设计、控制系统设计、算法设计具有非常重大的运用价值。在高原山地地区等特种环境下的机器人研发是未来军事化战略准备的重点研究方向,也是未来特种机器人的出发点。
机器人的执行单元是机器人受控制的核心单元,因此较好的执行器能够保障机器人的有效运动。电液伺服系统具有大功率、响应速度快、精度高等优点[1],被广泛应用于国防工业及国民经济各个领域。液压组件的功率-质量比更加大,相比于同等体积下的电机执行结构而言,更小的液压结构能够产生更加大的输出,力矩-惯量比大,载荷能力强,快速性高,系统响应快[2-3]。为了增大足式液压机械腿的载荷比和在复杂环境中的抗干扰性能,选用伺服液压系统作为机械腿的动力单元。PID控制因其不需要知道控制对象的精确模型、控制效果好、收敛快被广泛运用于工业控制中。充分考虑机器人腿部的非线性和在复杂环境下的工作情况,使用PID控制来设计腿部控制算法,实验中通过测试发现传统的PID控制存在控制精度差并且控制参数需要实时调节,不同测试压力下以及不同数量的液压缸运动时控制参数都需要做出相应的改变。为了解决PID参数需要实时调节的问题,引入自适应神经网络PID控制算法,通过对神经元权值以及神经元比例系数的不断修正达到自适应控制的目的[4]。实验结果表明,改进单神经网络PID相比于传统PID以及神经网络PID,能够更好地实现跟踪控制,能在线进行参数调节,控制效果好,鲁棒性强。
1 整体设计方案
1.1 阀控液压缸位置伺服系统
液压驱动关节的液压系统示意[5]及机械结构示意分别如图1、2所示。通过编码器采集关节旋转角度作为角度闭环控制系统的反馈信号;采用期望角度的控制信号控制伺服阀开口,通过驱动液压缸1活塞杆的伸出及缩回,实现对机械腿关节的角度闭环控制。
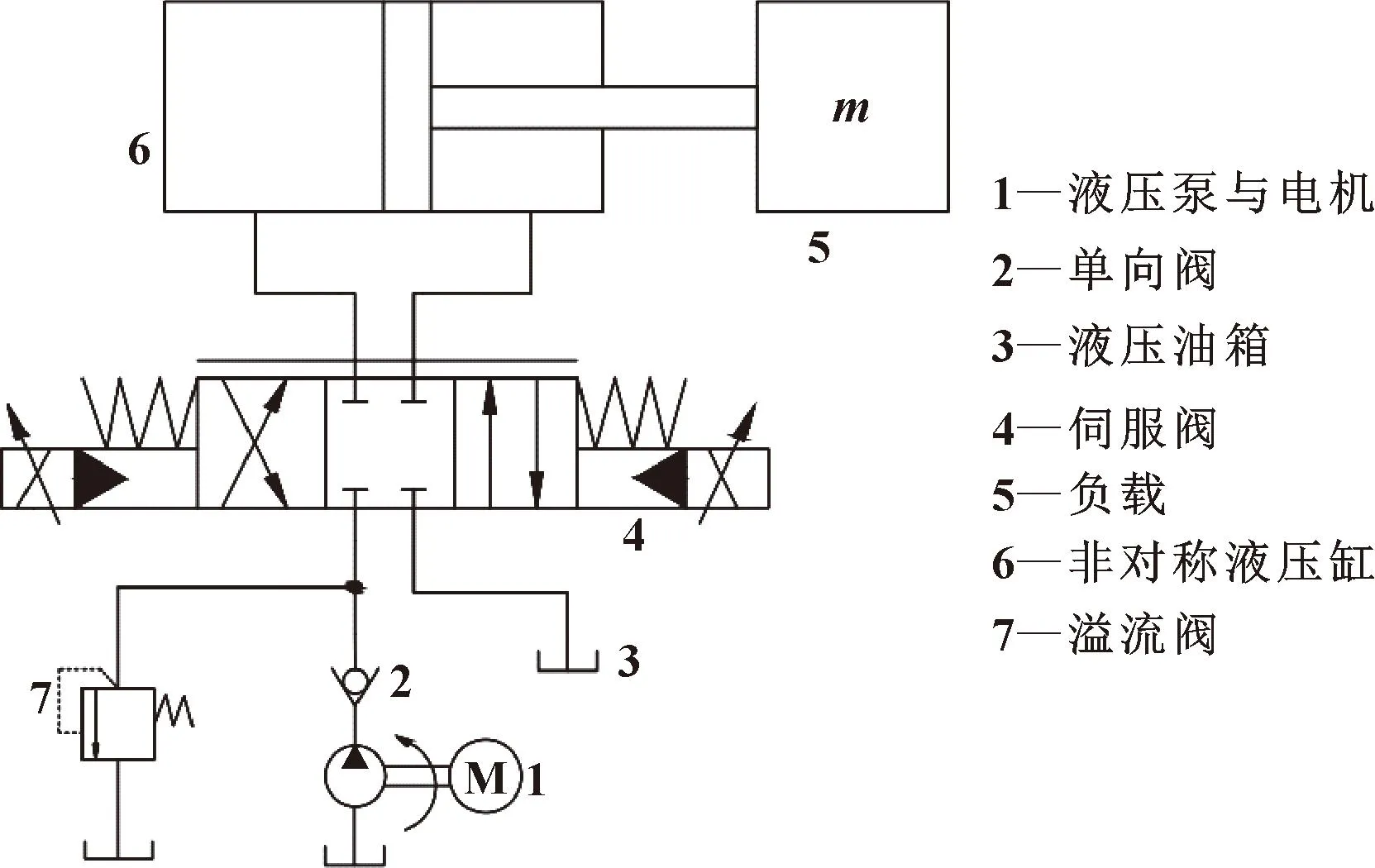
图1 阀控液压缸位置伺服系统示意
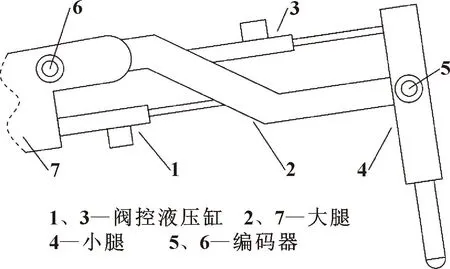
图2 机械腿关节结构示意
1.2 系统控制框图
液压机械腿的控制原理如图3所示,整个伺服系统采用阀控式电液伺服控制系统[6],电液伺服系统由伺服驱动器、功率放大元件、伺服阀、液压缸、传感器等组成[7]。

图3 液压机械腿控制框图
上位机通过串口发送初始的关节角度值θ0,STM32接收到角度值后通过运算转换成相应的输出电压值U(-10~10 V);伺服驱动器接收上一级的电压信号转成控制伺服阀的电流信号(-40~40 mA);伺服阀根据输入的电流改变阀的开度和阀芯的方向,进而控制液压缸朝着不同方向运动。
2 电液伺服系统建模
电液伺服阀可以看作一个二阶系统,空载时的传递函数为
(1)
式中:QL0为通过伺服阀的空载液压流量;i为通过伺服阀阀芯的电流;Ksv为伺服阀的静态增益;ωsv为伺服阀的固有频率;ξsv为伺服阀的阻尼比。
液压缸可以看作是三阶的非线性系统[8],液压缸的外部负载主要是惯性力负载[9],令其传递函数为
(2)
式中:xp为液压缸的位移;Ap为活塞杆位移时对应的等效工作面积;ωk为液压缸的固有频率;ξk为液压缸的阻尼比。
液压缸安装在机械腿的关节部位,刚体会承受机械结构带来的外部力矩以及在机械腿触地时带来的惯性冲击力,按照力学方程对液压缸建立的传递函数[10]为
(3)
式中:FL为作用在液压缸的活塞杆的力;Kce为流量压力系数;βe为等效容积的弹性模数;Vt为液压缸的有效容积。
图4为伺服控制系统的系统传递函数框图[11]。

图4 伺服控制系统的系统传递函数框图
系统的开环传递函数为
(4)
3 改进单神经网络PID控制算法
3.1 改进单神经元PID算法
神经网络(Neural Network)就是模拟人脑思维方式的数学模型[12-13]。在此次设计中,采用了结构简单、适应能力强、鲁棒性强的单神经元构成的单神经元自适应PID控制器[14],并加入了自调整算法形成改进单神经网络PID控制器。图5所示是改进单神经元自适应PID控制器结构。

图5 改进的单神经元自适应PID控制器结构
Yd为设定值,Y为对象跟踪值,通过状态转换器生成的x1、x2、x3作为神经元输入的信息,ω1、ω2、ω3是连接神经元的连接强度,即神经元的权值,神经元的输入输出关系[15]为
(5)
单神经元自适应控制器的自适应控制是通过调整权值ωi来实现自适应和自调整[16-17]。权值的调整在单元神经中按照有监督的Hebb学习规则进行学习,Hebb学习规则表达式为
Δωij(k)=η[dj(k)-oj(k)]oj(k)oi(k)
(6)
式中:oi表示神经元i的激活值;oj表示神经元j的激活值;ωij表示神经元i和神经元j的连接权值;dj是期望输出;η是学习速率。
至此已经把神经元的输入输出关系确定了。为了把神经元函数与PID控制结合,引入增量式PID[18]:
Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+KD[e(k)-2e(k-1)+e(k-2)]
(7)
令x1=e(k),x2=e(k)-e(k-1),x3=e(k)-2e(k-1)+e(k-2), 由式(5)(7)得单神经自适应PID[19]为
Δu(k)=ω1[e(k)-e(k-1)]+ω2e(k)+ω3[e(k)-2e(k-1)+e(k-2)]
(8)
ω1、ω2、ω3能够通过自我学习进行自适应调整,弥补了传统PID中KP、KI、KD不能随着内外系统参数改变自动调整的缺陷,大大提高了系统的鲁棒性[20]。由式(6)可知,在有监督的Hebb学习规则下,权值ω的调整规则如下,
Δωi(k)=ηu(k)e(k)xi(k)
(9)
由式(5)—(9)得,ω1、ω2、ω3自适应学习调整算法[21-22]如下:
(10)
式中:ηP、ηI、ηD分别为比例、积分、微分的学习速率,分别对权值进行调整;K为神经元的比例系数,K>0,K的值越大快速性越好,但是超调量会增大,系统稳定性变差,K的值过小则系统的快速性会降低。
自调整算法的输入以液压机械腿的关节角度的当前误差Ek、上一次的误差Ek-1以及误差变化Ek-1-Ek来实时调节K的值,调整算法如下:
K=Kp·Ek+Kv·∑Ek+Kd·(Ek-1-Ek)
(11)
式(11)中:Kp为位置比例系数,Kp的大小决定了液压缸伸缩过程中平均速度的大小;Kv为速度比例系数,Kv决定了液压缸能否稳定到达指定位置;Kd为误差变化比例系数,Kd起着对超调削弱的作用。
3.2 控制算法软件设计
控制系统的软件部分有STM32中的处理程序和上位机中的源参数信号发送和采集参数显示的程序,上位机主要实现与控制板之间的数字通信、命令传达和采集参数。控制板软件部分主要是处理上位机传达的命令并经过相关算法来控制伺服系统。图6所示为软件控制系统总体框图。

图6 软件控制系统总体框图
图7所示为程序中改进单神经元PID控制算法流程。位置比例系数Kp在误差Ek比较大的时候承担主导作用,神经元比例系数K受位置环影响大,从而快速缩短误差,加快响应速度。随着误差变小,位置环作用降低,当位置环的作用小于速度环的时候,此时速度环起主导作用,K主要受速度环影响,液压缸速度保持一定速度运行,并以最短时间达到设定值。误差变化环的作用是当位置未到达设置值的时候起到增强位置和速度环的作用,当液压缸在设定值附近剧烈震荡或者超调的时候减小震荡和超调。
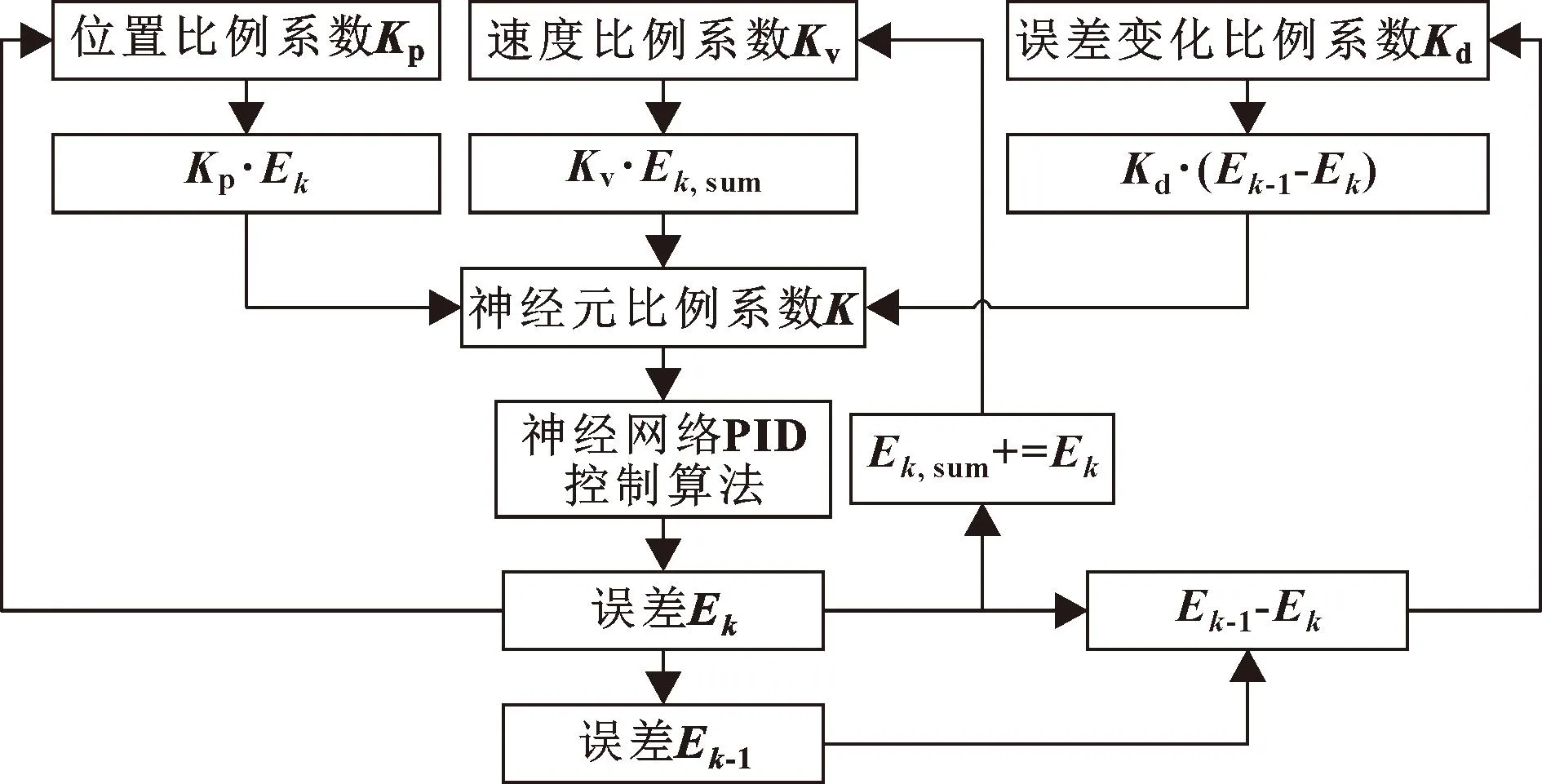
图7 改进单神经网络PID算法流程
上位机通过串口发送一串带有期望关节角度值的数据包给下位机,下位机采集机械腿实际的关节角度上传至上位机显示,如图8所示。当角度偏差大于1°,上位机中对应的角度指示灯会变红,提示当前轮控制并未结束。控制目标完成后指示灯常绿显示,提示对应关节已经达成目标控制要求。

图8 上位机数据采集与控制界面
4 电液伺服系统仿真与实验
4.1 电液伺服系统仿真
(12)

表1 伺服阀和液压缸内部参数
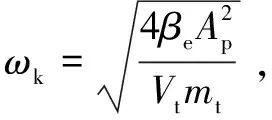
(13)
在Simulink中建立伺服系统仿真模型[24],在没有外界干扰的情况下,分别建立了传统PID和改进单神经网络PID的仿真模型,如图9—10所示,控制输入为阶跃信号和正弦信号。

图9 传统PID控制仿真模型

图10 改进单神经网络PID控制仿真模型
图11所示为传统PID、单神经网络PID和改进单神经网络PID对阶跃输入的响应输出及误差,对正弦信号的响应输出和跟踪误差如图12所示。可知:在较好参数的仿真情况下,改进单神经网络PID比单神经PID和传统PID的快速性和稳定性更好,两种跟踪误差均小于0.5 mm;改进单神经网络PID提高了跟踪速度和精度,超调量明显较小,具有很高的可靠性,同时在参数调节方面更加简便,只需要在实际运用中根据需要调整神经元比例系数的范围,简化了控制运算,具有更高的鲁棒性。

图11 阶跃响应(a)和阶跃误差(b)曲线
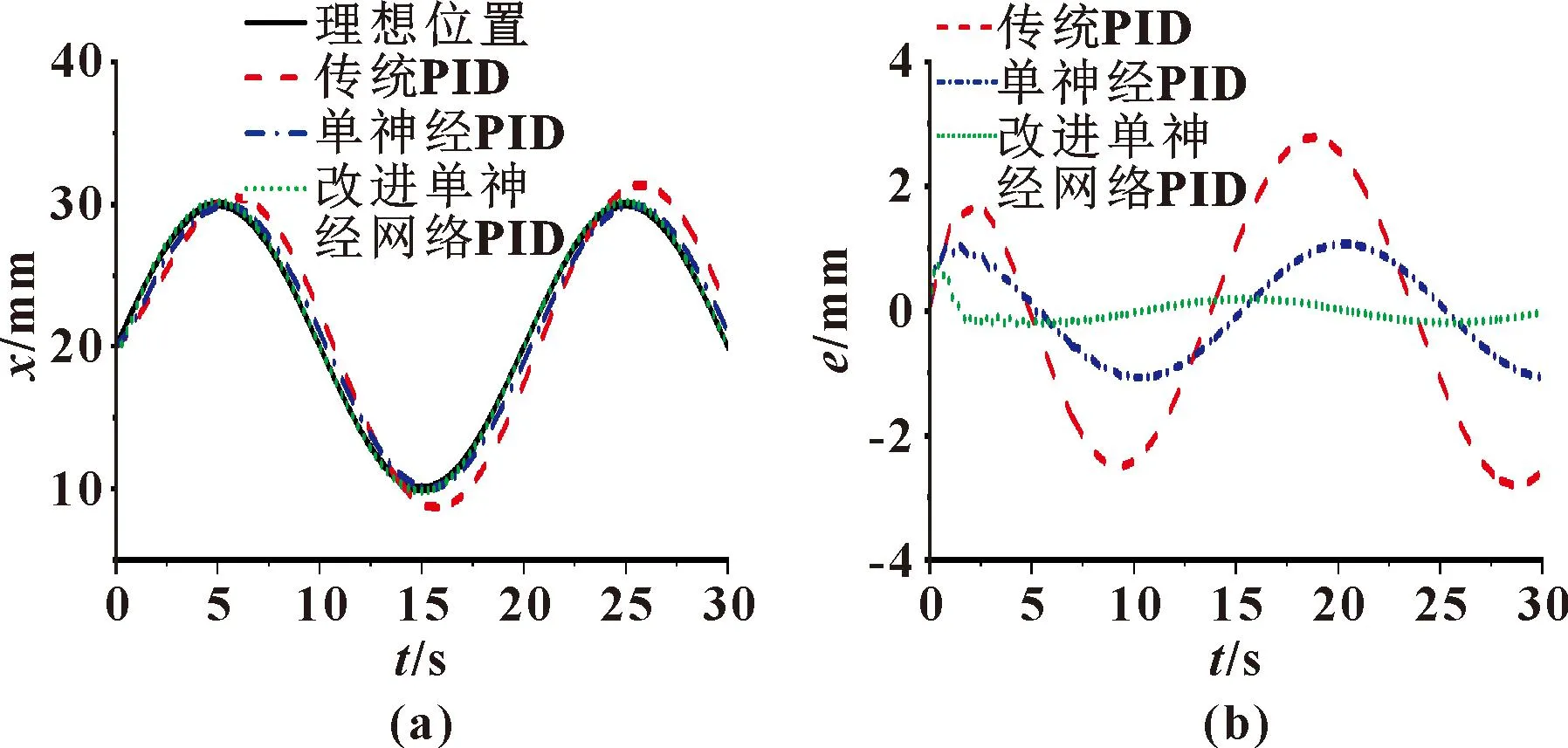
图12 正弦响应(a)和正弦误差(b)曲线
4.2 实验测试
为验证算法在足式机器人中的可行性,依托于现有的机器人样机进行了实地测试。图13所示为六足机器人测验平台。

图13 实验测试平台
设置初始油压为10 MPa条件下分别测试了改进单神经网络PID控制算法、单神经网络PID和传统PID控制算法对机械腿的控制效果,测试结果如图14所示。测试方法是关节角度从5°开始运动到48°,然后从48°运动回5°。改进单神经网络PID控制算法在关节角度增加和降低的情况下比其他两种算法都要收敛得快。图15所为关节角速度变化曲线,改进单神经网络PID角速度能在极短的时间内达到超过0.4 rad/s,单神经网络PID和传统PID控制算法最大的角速度才0.2 rad/s。根据角速度的变化图能够从侧面得知改进单神经网络PID的角加速度更大,灵活性更高,更加适合户外对机动性的要求。
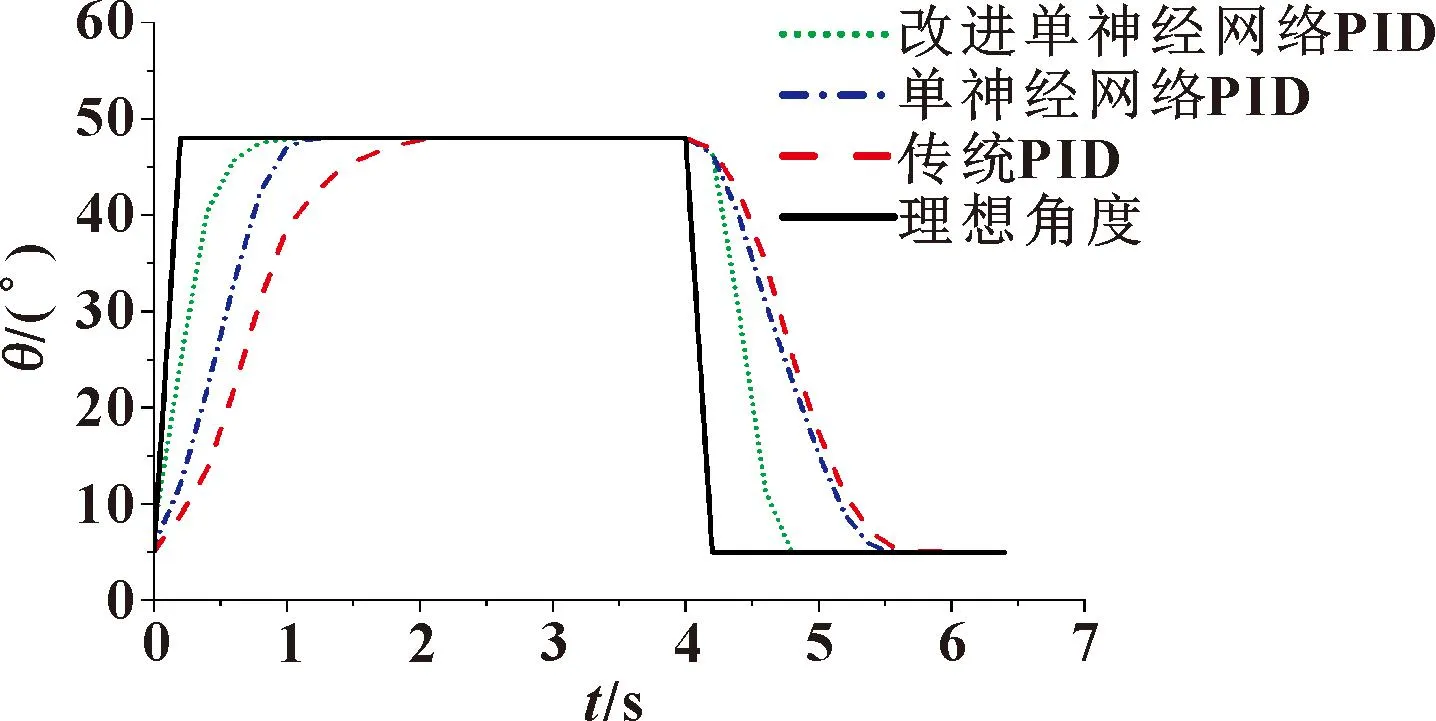
图14 三种PID算法实验角度测试曲线

图15 三种PID控制实验角速度测试曲线
为了验证算法对外部干扰信号的抗干扰能力,实验中通过添加冲击干扰验证3种PID控制算法对干扰的对抗性能。图16所示为冲击测试曲线,在相同的冲击干扰下,改进单神经网络PID对冲击干扰的抑制能力更强,恢复干扰产生的误差的速度更快,拥有更好的抗干扰能力。

图16 三种PID控制实验冲击测试曲线
从测试数据可以得出:改进单神经网络PID控制算法能够实现不同位置下的参数自整定,距离设定位置越远,此时输出信号对伺服阀的作用越强,能够实现初始动作的快速响应;随着距离设定角度值越来越近,位置环作用减弱,速度环作用增强,在速度环的作用下能精准达到指定角度位置,能够实现智能化控制,控制的稳定性高,无超调。相比传统PID和单神经网络PID,改进单神经网络PID在整个关节的运动过程中更加柔顺,快速性和准确性更好,能更好地适应高原山地环境中特种作业的需求。
5 结论
针对机器人腿部运动控制对快速性、可靠性的需求以及在复杂环境中机器人模型难以精确的问题设计了在机器人底层运动控制中能够实现自适应快速调节的控制算法,改进后的算法既结合了传统PID算法不需要十分精确的被控对象模型就能实现较好的控制效果,又优化了神经网络在复杂控制算法中会陷入局部最优解的问题,能够十分快速精确地达到控制效果,这是机器人底层运动控制最主要的需求。从实验结果来看,改进单神经网络PID控制算法能够在机械腿运动过程中实现参数自整定,它的运动柔顺性高,响应快速性快,控制精度高,稳定性和鲁棒性强,能够很好地运用于液压六足机器人的运动控制中,具有较好的实际运用价值。
