基于向量最值(或范围)问题的解题教学

⦿ 江苏省东海县第二高级中学 胡陈梅

平面向量的范围与最值问题是热点问题,也是难点问题.此类问题综合性强,体现了知识的交汇整合,其基本题型是根据已知条件求某个变量的范围、最值,比如,向量的模、数量积、向量夹角、系数的范围等;解决思路是建立目标函数的解析式,转化为求函数的最值,同时向量兼有“数”与“形”双重身份,故平面向量的范围与最值问题的另一种思路是数形结合.

题型1与系数有关的最值(范围)问题

图1

分析：根据题设条件,通过平面向量的线性表示与转化,利用线性组合的构建,结合三点共线的等价条件得到系数x,y之间的等量关系,代入目标关系式进行消参处理,进而利用基本不等式加以放缩处理,得以确定系数关系式的最值问题.

感悟提升：解此类问题一般分两步走.第一步,利用平面向量的运算、性质等将问题中的系数等相关信息转化为相应的等式关系;第二步,运用基本不等式或函数的性质求其最值.

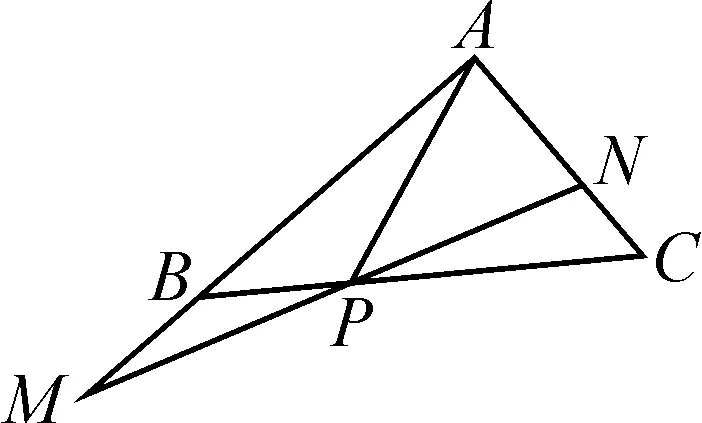
图2

题型2与数量积有关的最值(范围)问题

分析：根据平面向量的数量积的定义a·b=|a||b|cosα,借助两向量的夹角的构建与应用来合理变形与转化,通过平面几何思维来直观,有时也是解决此类问题时比较常用的一种技巧方法.这里要注意的是平面向量的夹角应与平面几何中的对应角加以联系,结合图形直观来分析即可.

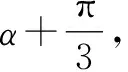
图3

感悟提升：求数量积的最值(范围)的方法通常有两种.(1)坐标法.通过建立直角坐标系,运用向量的坐标运算转化为代数问题处理;(2)向量法.运用向量数量积的定义、不等式、极化恒等式等有关向量知识解决.

题型3与模有关的最值(范围)问题

例3已知平面向量a,b,c满足|a|=1,b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).

分析：根据平面向量的“数”的结构属性,构建平面直角坐标系,合理引入平面向量的坐标,利用平面向量中的相关要素,转化为涉及坐标的函数、方程或不等式等,进而从代数视角来数学运算与逻辑推理.这里通过平面向量所对应的坐标的构建,利用题设条件确定对应坐标的关系式,再利用基本不等式、三角函数的应用等来确定最值.

解析：在平面直角坐标系xOy中,设向量a=(1,0),b=(x1,y1),c=(x2,y2),如图4所示.

图4

感悟提升：求向量模的最值(范围)的方法通常有两种.(1)代数法.把所求的模表示成某个变量的函数,或通过建立平面直角坐标系,借助向量的坐标表示;需要构造不等式,利用基本不等式、三角函数,再用求最值的方法求解.(2)几何法(数形结合法).弄清所求的模表示的几何意义,注意题目中所给的垂直、平行,以及其他数量关系,合理的转化,使得过程更加简单;结合动点表示的图形求解.

针对训练若向量a,b互相垂直,且满足(a+b)·(2a-b)=2,则|a+b|的最小值为( ).

题型4与夹角有关的最值(范围)问题

例4平面向量a,b满足|a-b|=3,|a|=2|b|,则a-b与a夹角最大时,|a|为( ).

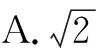
分析：根据题设,由平面向量的数量积运算加以合理变形与转化,通过平面向量的夹角公式合理消参,利用基本不等式的应用进行放缩,进而确定夹角的余弦值的最小值,利用三角函数的性质来进一步分析与处理.

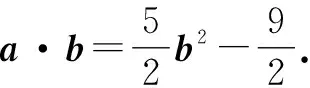
感悟提升：求夹角的最值(范围)问题时,往往要选取对应夹角的三角函数值,以选取夹角余弦值为主,通过余弦值的三角函数表达式,利用关系式的变形与转化,采用基本不等式或函数的性质进行求解.

平面向量中的最值(范围)问题,是高考对平面向量比较常见的考查形式之一,也是常考常新的基本考点之一,主要考查的知识点涉及平面向量的模、坐标、夹角、数量积以及相关的参数等.在实际解答与应用时,挖掘题目内涵,结合题意,从平面向量的本质出发,选取函数法、三角法、不等式法、图形法等行之有效的基本方法来解决,进而达到解决相关的最值(范围)问题的目的.