美从对称中来:浅谈数学核心素养的培养

⦿ 安徽省合肥市第一中学 温海平 刘 娟

要提高学生的数学核心素养,就必须教会学生解决数学问题.本文中将从两道高考题说起,抛砖引玉,探索在平时教学中提升学生的数学核心素养的路径,以飨读者.

1 试题呈现

试题1(2022年新高考Ⅰ卷)已知函数f(x)=x3-x+1,则( ).

A.f(x)有两个极值点

B.f(x)有三个零点

C.点(0,1)是曲线y=f(x)的对称中心

D.直线y=2x是曲线y=f(x)的切线

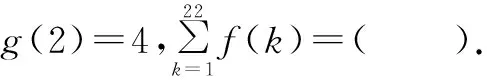
A.-21 B.-22 C.-23 D.-24

2 考题分析

这两道试题都有一个共同点,就是考查函数的对称性.对称,是一种数学美.我们在做题时,通常会数形结合,在欣赏数学美的同时,数学抽象、逻辑推理、数学运算等数学核心素养也在这两道题里得到了充分的考查,可谓随“卷”潜入“题”,润“人”细无声[1].

高考对数学的考查,正从知识走向能力,从能力走向素养.有人说,初中课上教你包饺子,考试就考包饺子.到了高中,课上教你包饺子,作业是蒸包子,考试的时候却是烙馅饼.这个比喻很形象,就是说生搬硬套、照猫画虎这套在高中行不通了.我们要教会学生转变学习观念,做到举一反三,学会知识能力的迁移,提升自己的思维品质.

高考对这两道题共性的考查,明确了数学核心素养的形成,不是通过简单的刷题及题海战就可以了的.我们要教会学生构建自己的知识库,形成自己的知识体系.

3 追本溯源

教材对于对称的描述其实是有据可考的.人教A版(2019)教材必修第一册第87页有这样一道题:

我们知道,函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数,有同学发现可以将其推广为:函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

(1)求函数f(x)=x3-3x2图象的对称中心;

(2)类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是y=f(x)为偶函数”的一个推广结论.

为了方便表述,本文将这个推广结论记为定理1.

定理1函数y=f(x)的图象关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

这个定理的证明比较简单,本文从略.在定理1的证明过程中,还可以生成定理2.

定理2函数y=f(x)的图象关于P(a,b)成中心对称图形的充要条件是f(x)+f(2a-x)=2b.

试题1的选项C可由定理1轻松解决,这里不再赘述.引导学生深入思考:三次函数f(x)=ax3+bx2+cx+d(a≠0)都有对称中心吗?如果有,对称中心是什么?为什么会有这样的结论?

4 本质透析

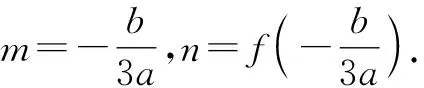
5 降维打击

从高观点看三次函数的对称性,观察函数f(x)=x3-3x2的图象(图1),由对称性可知,它的对称中心必定是函数的凹凸转折点(1,f(1)),即拐点,参考高等数学对拐点的定义:若方程f″(x)=0有实数解x0,那么(x0,f(x0))称为函数的拐点.

图1

图2

再回到课本,类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是y=f(x)为偶函数”的一个推广结论.为了方便表述,将这个推广结论记为定理3.

定理3函数y=f(x)的图象关于直线x=a对称的充要条件是y=f(x+a)为偶函数.

定理4函数y=f(x)的图象关于直线x=a对称的充要条件是f(x+a)=f(-x+a).

再看试题2,考查函数的对称性、周期性,属于拔高题.

因为g(x)的图象关于直线x=2对称,则有g(2-x)=g(2+x),代入f(x)+g(2-x)=5,可得f(x)+g(2+x)=5(记为①).又f(-x)+g(2+x)=5(记为②),由①②可得f(x)=f(-x),故f(x)是偶函数.由g(x)-f(x-4)=7,可得g(x+2)-f(x-2)=7.

结合f(x)+g(2+x)=5,消去g(x+2),得f(x)+f(x-2)=-2(记为③),所以f(-x)+f(x-2)=-2(记为④).

因此,f(x)的图象关于点(-1,-1)对称.又f(x)关于y轴对称,所以f(x)的最小正周期是4.

在①中,令x=0,可得f(0)=1.在③中,令x=1,可得f(1)=-1.在④中,分别令x=0,x=3,x=4可得f(2)=-3,f(3)=-1,f(4)=1.

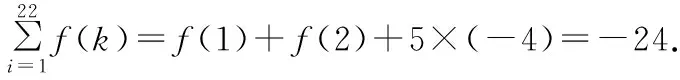
另解:由f(x)+f(x-2)=-2,考虑到x只能取整数,所以可将f(x)视为某种特殊数列,它的相邻奇数项且相邻偶数项的和均为-2,也可以算得答案为-24.

6 举一反三

在课堂教学中,教师要不断寻找时机,通过问题的变化,举一反三,不断刺激学生神经的兴奋点,从而达到良好的教学效果.问题的设置点不能太高,要让学生跳一跳、蹦一蹦就能找到触碰点,让好奇心成为引领他们探究问题的动力.

明白这些道理后,我们再看下面这道高考题.

C.f(-1)=f(4) D.g(-1)=g(2)

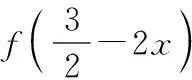
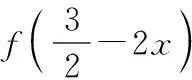
事实上,这类题型在历年的高考卷中出现过多次,这里不再一一列举.

从初中的一次函数、二次函数、反比例函数到高中的指数型函数、对数型函数、幂函数,尤其是三角函数,处处都彰显出对称美.若不能看透问题的本质,就会无从下手.若能从对称的角度看待问题,那么就会山穷水尽疑无路,柳暗花明又一村.如果平时的教学中渗透了相关知识,那么这种题型还是很简单的.

在教学过程中可以引导学生构建自己的知识资源库,把“对称”作为一个专题进行系统学习.利用现代教学软件Geogebra或几何画板画出每类函数的代表图形,加深学生对于对称的直观理解.通过对近几年的高考题的研究发现,有关对称的考查还是比较多的.学生核心素养的考查在近年的高考试题中也都有很好的体现,它指引着高中数学课程教与学的方向.

7 教学启示

俗话说得好,授人以鱼不如授人以渔.作为教师的我们既要立足课本,研读教材,又要深挖内涵,勤研善教,以不变应万变.波利亚告诉我们:没有任何一道题目是彻底完成了的,总还会有些事情可以做[2].

不畏浮云遮望眼,只缘身在最高层.只有自身的能力得到提升,才能更好地教育学生.因此,我们在教学过程中,不能只停留在解出一道题的层面,要反思解题过程以及在解题过程中遇到的问题.解题过程中学生会冒出各种奇思妙想,这些想法就是一朵朵思维的火花,教师要善于抓住时机,一步步引导学生去发现数学之美,那么他们就会离美丽的数学殿堂更进一步.