基于多队列的机场旅客安检流程仿真研究

赵振武，郑文悦，张沉沉

（中国民航大学安全科学与工程学院，天津 300300）

近年来，随着机场旅客吞吐量逐渐增长，传统安检方式下的旅客安检时间已无法满足旅客对于机场安检快速、便捷的需求。由于设备、安检人员操作、安检空间、法律法规等多方面的限制，不易通过改变旅客安检流程来提高安检效率。排队是旅客安检过程中不可或缺的活动，受到国内外学者的广泛研究。Li 等[1]首次建立了不同的旅客安检排队策略模型，展示了其潜在的网络结构，并比较了其在机场安检点排队中应用的不同性能情况。彭凯贝等[2]基于旅客风险等级分类的安检流程，提出安检排队优化策略，但其研究对象为铁路旅客安检。Mao 等[3]使用排队模型检查机场的安检点和人员配备，找出影响旅客吞吐量的潜在瓶颈，并通过数学公式推导出提高交通量和减少旅客等待时间的方法。Regattieri 等[4]提出了一种基于M/M/m排队模型的方法，根据不同的输入参数范围对系统性能进行参数分析，帮助解决生产系统和服务中的几个典型问题。Naji 等[5]提出了一种基于排队理论和粒子群优化（QT-PSO，queueing theory augmented with particle swarm optimisation）的预测旅客安检等待时间的新方法，在预测旅客平均等待时间方面优于现有方法。

上述研究大多是对旅客安检排队进行理论分析，而探索不同排队方式对安检效率的影响并采用仿真方法对其进行分析的研究较少。经典排队论的解析法在求解时容易忽略随机性因素对系统的影响。而系统仿真的方法不局限于数学公式，通过建模展现研究对象的物理特性与逻辑结构，不仅贴合实际，还可以更好地处理随机性因素的影响。本文利用AnyLogic 软件，结合排队论和社会力模型，使用机场安检通道的实际数据并参考相关文献，对6 种机场旅客安检排队方式进行建模仿真，通过计算、分析和对比找到效果最优的排队方式，以期为提高机场安检效率及后续机场旅客安检改进提供参考。

1 M/M/n 和n 个M/M/1 排队模型的对比

排队系统的基本组成部分主要有输入过程、排队规则和服务机构。机场旅客安检的排队规则属于等待制系统，即先到先服务的排队规则，而等待制排队系统中最常见的模型为M/M/n/∞，因此选择研究M/M/n和n 个M/M/1 排队模型。本节主要研究在相同的旅客到达、服务台数目和先到先服务规则的前提下，两种排队系统在性能上的差异。

理论上，利用利特尔法则（Little's law）求解可知，多个并列服务台的排队系统，排成单队比排成并列多队的方式具有显著优越性，即M/M/n 比n 个M/M/1 排队模型的性能表现优越[6]。

仿真上，在AnyLogic 软件中建立M/M/n 和n 个M/M/1 两种排队模型的仿真模型，并进行分析。理论研究的案例是M/M/3 和3 个M/M/1 排队模型的对比，仿真分析选取同样的模型进行对比，如图1 所示。模型中设置初始旅客总数为500 人，仿真模型的步长等于相继到达的2 个旅客的时间间隔。该时间间隔服从1/0.9的指数分布，因此旅客到达率为0.9。随着模型运行时间增加，旅客按照设定状态进入模型中，直到旅客总数减少为0，模型运行结束。运行结果如表1 所示。

仿真研究发现，M/M/3 和3 个M/M/1 排队模型相比，在平均队长、最大队长和服务台利用率3 个性能指标上都呈劣势。仿真结果表明3 个M/M/1 排队模型在性能表现上优于M/M/3 排队模型，与理论结果相反。实际上，基于解析法求解的排队理论存在部分缺陷，排队系统中的随机因素难以用解析法实现，导致理论结果与仿真运行的结果存在偏差。通常研究排队问题的学者从理论出发，关注旅客到达和接受服务过程服从的分布。然而实际的旅客到达过程不是简单的泊松分布，安检系统有多个服务节点，旅客接受服务的过程也不是简单的k 阶爱尔朗分布，并且机场旅客安检排队是串并联混合的状态，各个服务节点难以用数学模型描述。因此，仿真的方法能够更加贴合实际情况，利用该方法探索更有效的机场安检排队方式具有现实意义。

2 仿真模型建立

2.1 建立流程模型

机场旅客安检系统的主要流程如图2 所示，包括验证旅客证件、随身行李检查和人身检查。其中验证旅客证件的服务位置定义为验证服务台。

图2 机场旅客安检流程Fig.2 Security check process for airport passenger

安检过程中，旅客会受到人与人、人与障碍物及人与周围环境之间的相互作用，这3 种力的合力称为社会力[7]。AnyLogic 软件的行人库是基于社会力模型的。本文选择利用仿真软件对机场旅客安检进行仿真，既可以直观全面地得到旅客安检的数据，也可以将社会力模型的影响考虑在内。

考虑到M/M/n/∞排队模型在机场安检中的现实可行性，本文选择1 对1 且验证服务台靠近安检通道放置（A1）、1 对1 且验证服务台远离安检通道放置（A2）、1 对2 且验证服务台靠近安检通道放置（B1）、1 对2 且验证服务台远离安检通道放置（B2）、1 对4 且验证服务台靠近安检通道放置（C1）、1 对4 且验证服务台远离安检通道放置（C2）6 种排队方式。首先固定一个验证服务台远离安检通道放置的距离，分别找到低、中、高峰时段性能表现最优的排队方式，如果最优排队方式的验证服务台远离安检通道放置，则考虑最优距离。由于机场安检空间及安检费用的限制，并且验证服务台与安检通道的距离越远，旅客此段路程耗费的时间越久。因此，本文选择将验证服务台远离安检通道1～20 m，每隔1 m 放置，找到最优距离。目前大部分机场旅客安检的传统排队方式为A1。1 对1、1 对2、1 对4的排队方式如图3 所示。验证服务台靠近和远离安检通道放置如图4 所示。靠近时，旅客验证身份后，只能进入该验证服务台对应的安检通道；远离时，旅客验证身份后，可以自主选择安检通道进行安检。

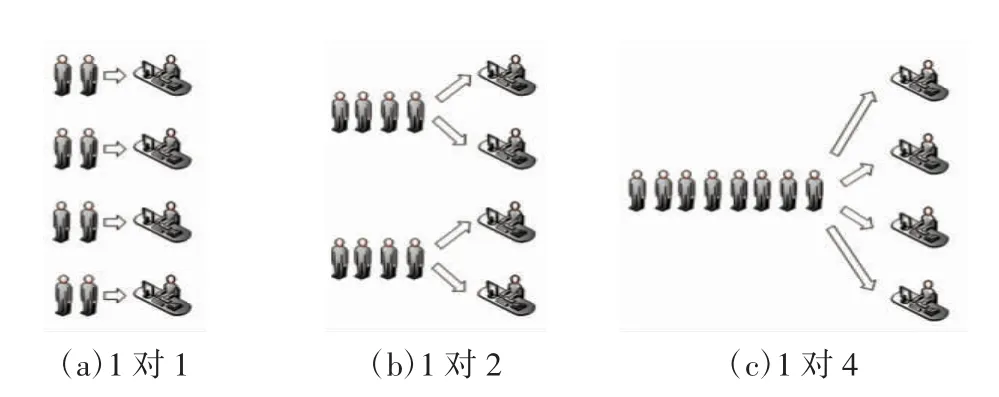
图3 排队方式Fig.3 Way of queuing

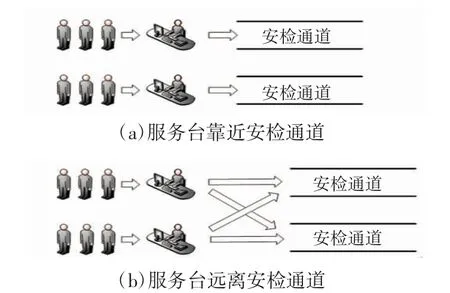
图4 验证服务台放置方式Fig.4 Placement of verification service desk

旅客agent 模型的设计是保证仿真结果与现实情况相符的重点环节，首先确定旅客agent 模型处于整个机场安检环境中，其次确定旅客agent 模型的属性和行为。旅客agent 的属性包括旅客的行走速度、个体直径、是否携带随身行李；旅客agent 的行为包括旅客到达安检通道的速率、经过安检后旅客和行李的匹配、安检通道内人数的控制。在AnyLogic 软件中利用“Split”和“Match”两个模块结合java 语言实现旅客与行李的一一匹配，“Split”模块的功能是将人与行李分离，利用“agent.id=original.id”语句赋予每位旅客与每个行李对应的id，此后旅客与行李分别进行安检，再通过“Match”模块中设定的“agent1.id==agent2.id”语句，使每位旅客在安检后能够与自己的行李正确匹配；利用“hold”模块结合java 语言实现安检通道内人数的控制，建立条件变量“variable”及事件“event”，在“event”中输入程序如式（1）的java 语言，即

再将“variable”“event”与“hold”关联起来，即可控制正常运行时安检通道内的人数。

在AnyLogic 软件中绘制出旅客到达、排队等待进入安检通道、旅客放下随身行李、旅客及随身行李通过安检（旅客安检按性别分开）、旅客拿起随身行李（涉及到初检报警和开包检查的概率）、旅客退出安检等机场旅客安检流程。最终建立的机场旅客安检单通道流程模型如图5 所示。

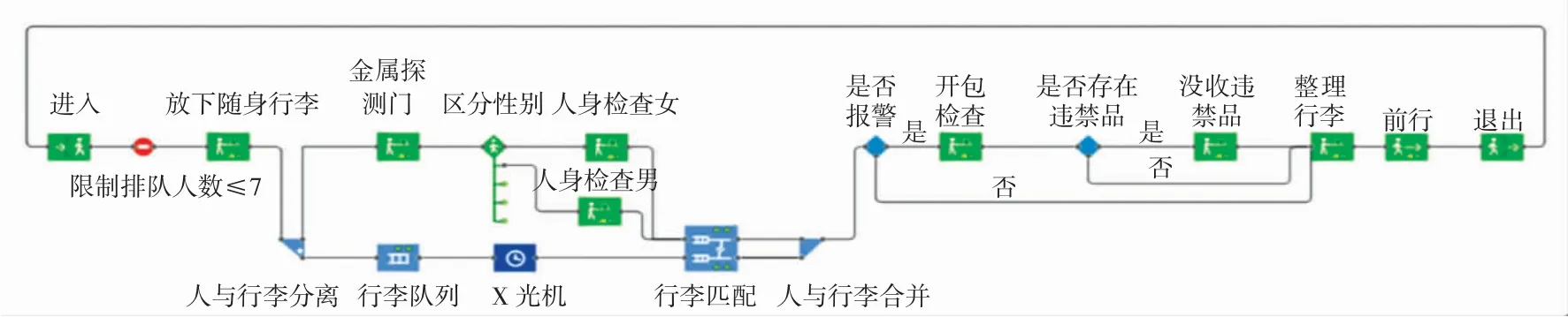
图5 机场旅客安检单通道流程模型Fig.5 Model of single-channel security check process for airport passenger

2.2 建立环境模型

依据国内某大型机场的安检布局及空间尺寸，如表2 所示，建立流程模型对应的环境模型。1 对4 的排队方式机场旅客安检系统至少有4 个安检通道，因此，本文建立的仿真模型有4 个安检通道。机场旅客安检环境模型的3D 效果如图6 所示，此图中的验证服务台靠近安检通道放置。

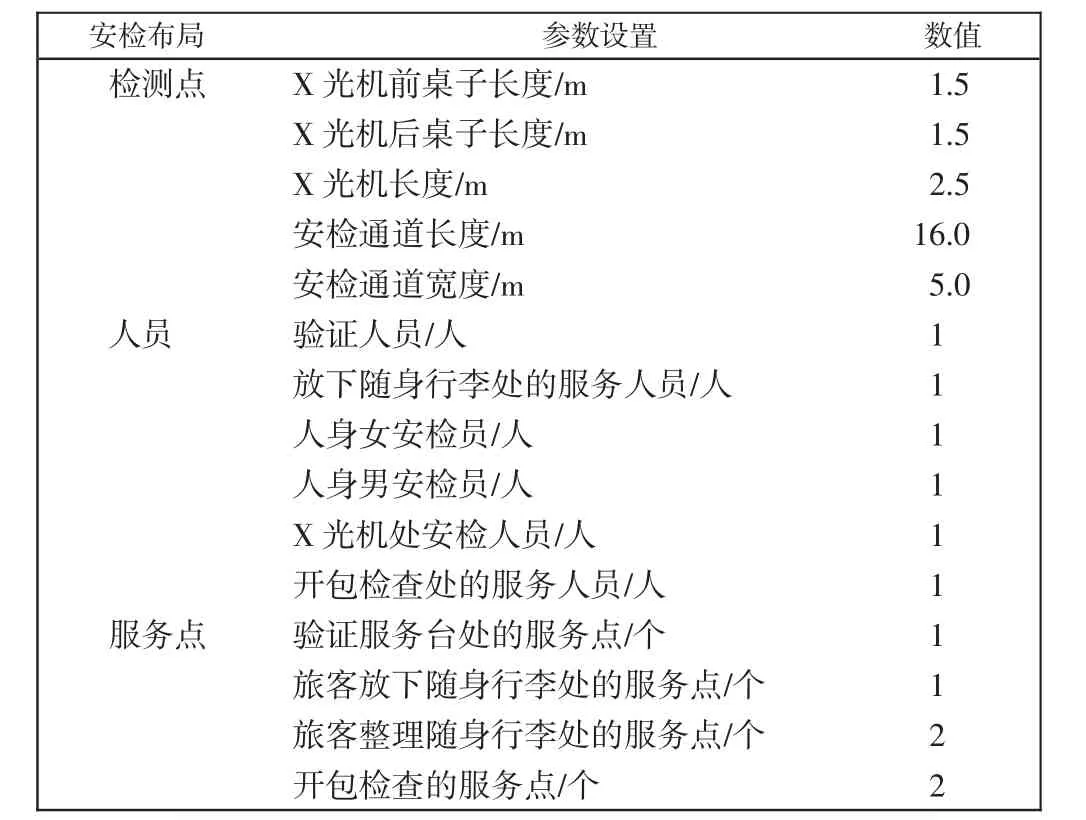
表2 国内某机场的安检布局及空间尺寸Tab.2 Security check layout and space size of an airport in China

图6 机场旅客安检环境模型的3D 效果Fig.6 3D effect of security check environment model for airport passenger

3 输入数据

3.1 旅客参数

旅客参数包括行走速度和个体直径。本文结合旅客在机场中的实际情况以及相关文献进行设置。旅客正常的行走速度会受到性别、年龄、身体状况、习惯等多方面的影响，将初始速度设置为0.3～0.7 m/s，服从均匀分布，舒适速度设置为1.15～1.55 m/s，服从均匀分布。旅客个体直径受到旅客自身体型及随身携带的行李影响，将旅客个体直径设置为0.5～0.6 m，服从均匀分布。

3.2 运行参数

结合机场实际运行情况及相关文献对运行参数进行设置。对放下随身行李时间、通过金属探测门的时间、男性人身安检员检查时间、女性人身安检员检查时间、X 光机检查时间、整理行李时间、开包检查时间数据进行拟合，对于拟合后的分布及计算后得到的分布进行检验，以上时间分布全部通过检验，则最终建立的安检通道流程中各个模块参数[8-15]如表3 所示，其中：triangular（）表示三角分布，uniform（）表示均匀分布。

表3 模型运行参数设置Tab.3 Parameter setting of model operation

3.3 旅客到达率

国内某机场一天内4 个安检通道各时段的旅客到达情况如图7 所示。文中的旅客与运行参数设置来自于实际机场运行情况及相关文献，为了进一步验证仿真模型参数设置的准确性，选取9：00—10：00 的客流量692 人对模型进行校验，运行结果与实际情况相符，由此证明仿真模型中旅客与运行参数设置准确。从图7 可以看出，全天客流量变化较大，存在低、中、高峰时段，并且未来机场吞吐量还会不断增加，为了综合考虑不同旅客流量的影响，选取低、中、高峰的旅客到达量进行仿真分析，由于300 人/h 以下的低峰客流基本上不形成排队，如21：00 —22：00 的旅客到达量为272 人，旅客无须排队即可进行安检，本文对300 人/h以上的旅客到达率进行研究。最终选取20：00—21：00的低峰客流402 人、11：00—12：00 的中峰客流623 人、7：00—8：00 的高峰客流802 人作为仿真模型输入的旅客到达率。

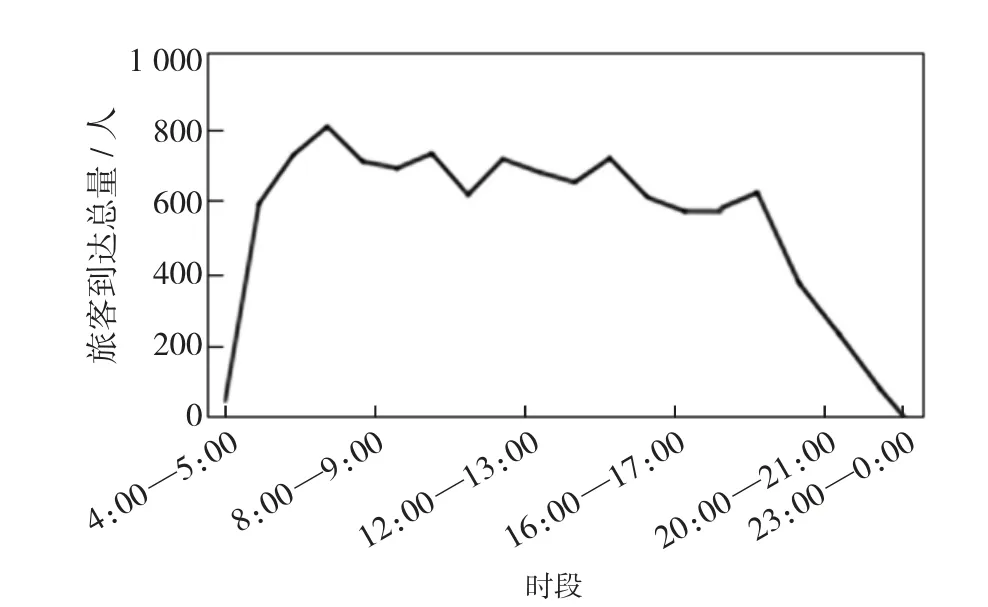
图7 一天内4 个安检通道各时段的旅客到达情况Fig.7 Passenger arrivals at all times of the day at the four security check

4 仿真结果及分析

本文统计6 种排队方式运行后的4 个性能指标，用来比较分析每种排队方式的性能，分别为：

（1）安检总时间，表示第一个旅客进入系统和最后一个旅客离开系统之间的时间间隔；

（2）平均单队列人数，表示旅客排队时单个队列人数的平均值；

（3）旅客平均等待时间，表示从旅客进入队列到验证开始所用的平均时间；

（4）安检平均服务时间，表示旅客从进入验证到整理行李结束所用的平均时间，不包含旅客从验证服务台走到安检通道口的时间。

4.1 最优排队方式分析

安检总时间为旅客到达率选取402、623、802 人/h时，通过建立的仿真模型分别检查500 名旅客安检所花费的总时间来衡量的，因此，安检总时间越少，系统的性能越好。每种情况仿真模型运行10 次产生10 个安检总时间取平均值，通过计算得到旅客到达率为402、623、802 人/h 时的不同排队方式箱线图，如图8—图10 所示。

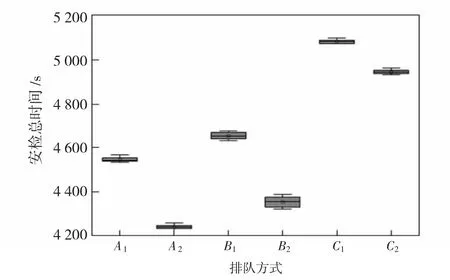
图8 旅客到达率为402 人/h 的不同排队方式安检时间Fig.8 Security check time at passenger arrival rate of 402 p/h with different queuing methods

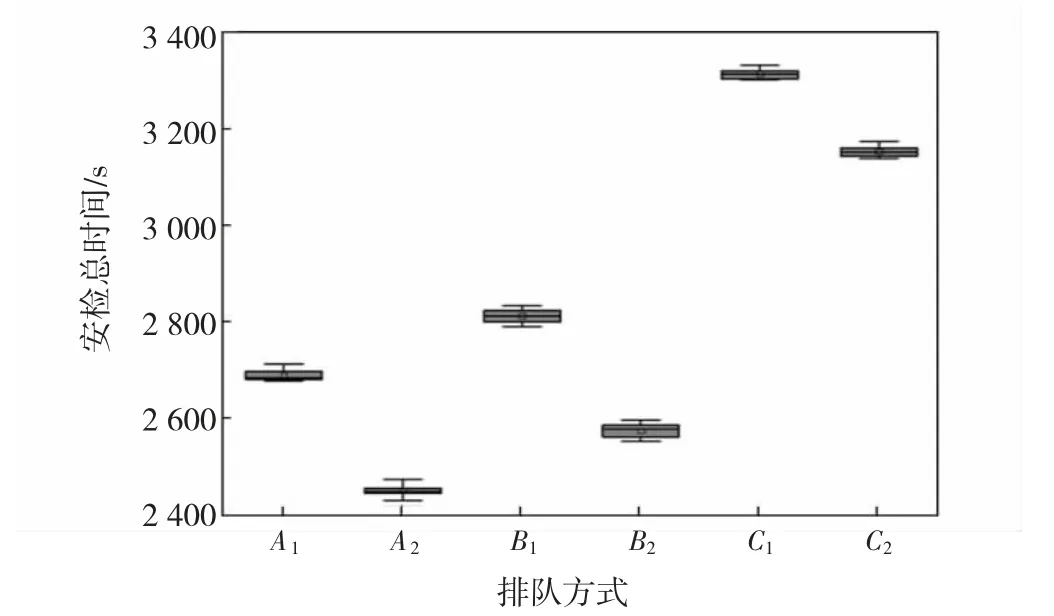
图9 旅客到达率为623 人/h 的不同排队方式安检时间Fig.9 Security check time at passenger arrival rate of 623 p/h with different queuing methods

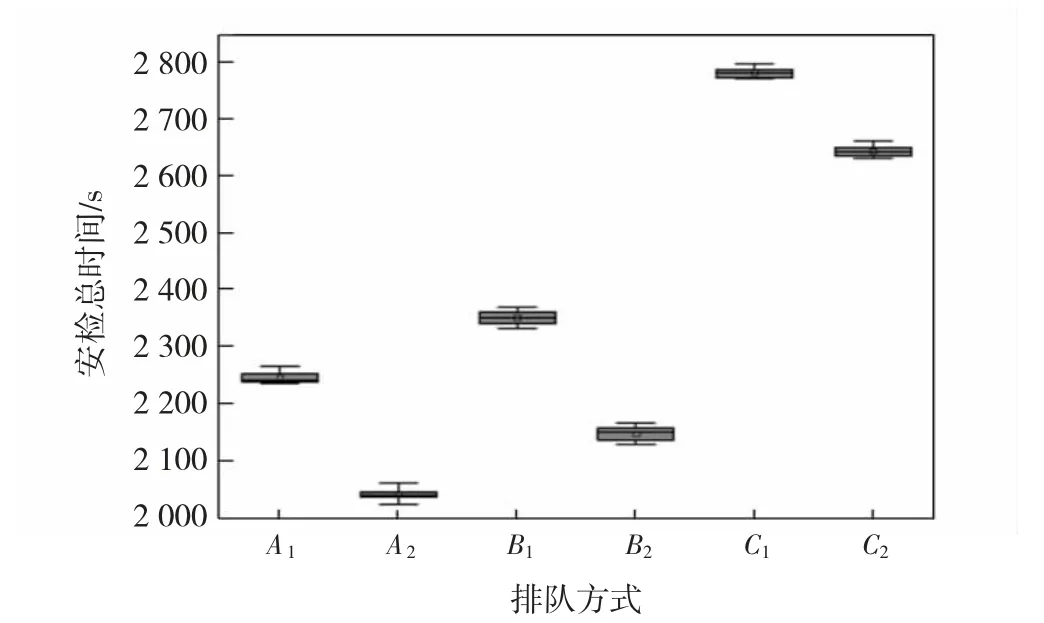
图10 旅客到达率为802 人/h 的不同排队方式安检时间Fig.10 Security check time at passenger arrival rate of 802 p/h with different queuing methods

从图8—图10 可以看出，在低、中、高峰客流量的情况下，A2的安检总时间始终保持最少。

对其余3 个性能指标进行分析，固定验证服务台到安检通道的距离为15 m，旅客到达率分别选取402、623、802 人/h，对6 种排队方式各进行20 次仿真，运行结果如表4—表6 所示。

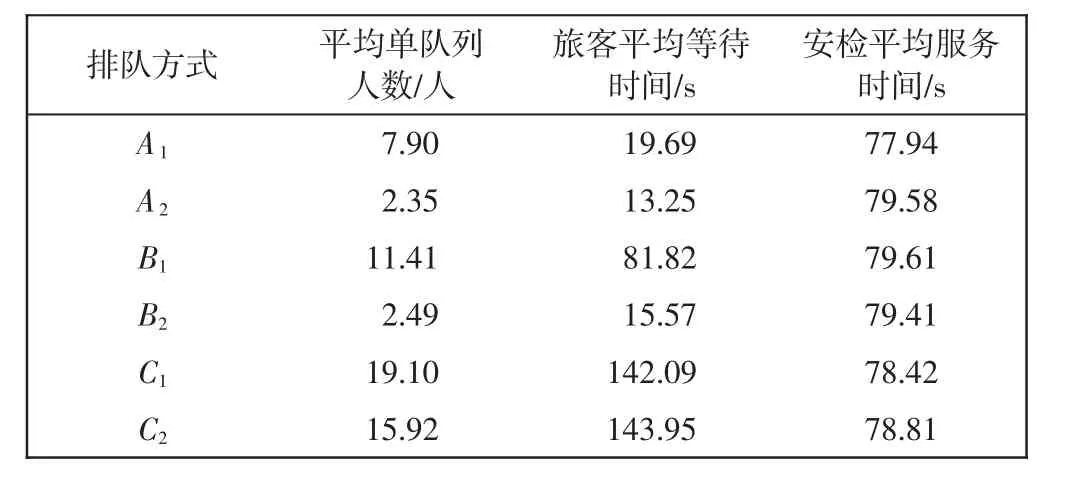
表4 旅客到达率为402 人/h 的运行结果Tab.4 Results at passenger arrival rate of 402 p/h

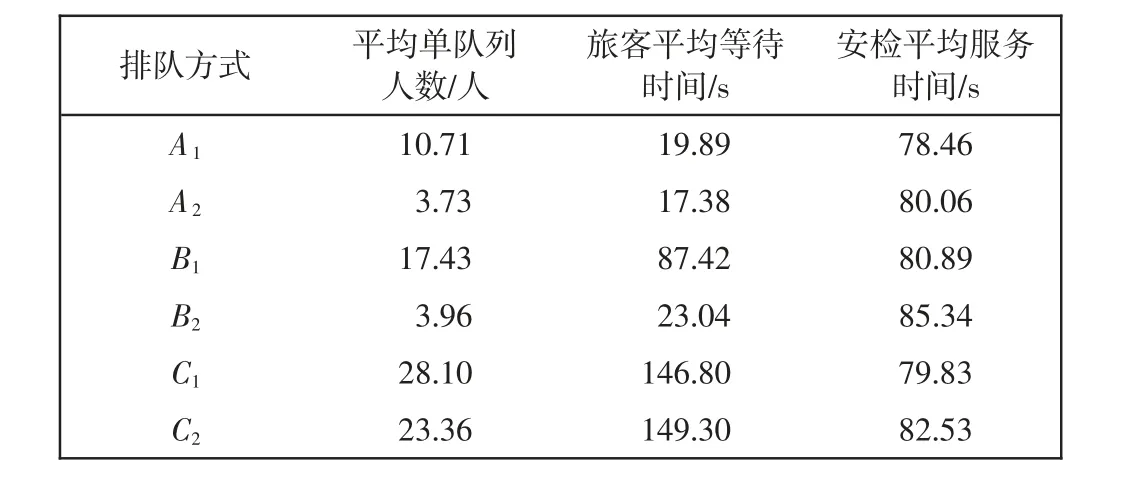
表5 旅客到达率为623 人/h 的运行结果Tab.5 Results at passenger arrival rate of 623 p/h

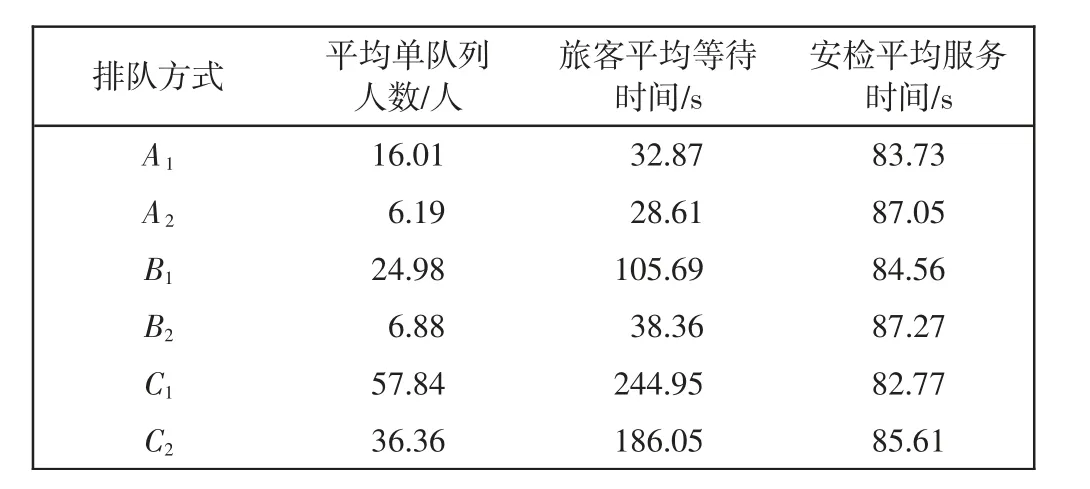
表6 旅客到达率为802 人/h 的运行结果Tab.6 Results at passenger arrival rate of 802 p/h

对表4—表6 的数据对比分析得到，在旅客到达率为402、623、802 人/h 时，A2的旅客平均等待时间和安检平均服务时间的总计用时比其他5 种排队方式更短，且A2的旅客平均等待时间更短，说明将验证服务台前提可以缓解此处的服务压力，从而提高旅客安检效率。且A2的队列长度表现最好，因此，A2的表现效果更好。

通过上述分析，可以得到最优排队方式是A2，即1对1 且验证服务台远离安检通道放置。

4.2 验证服务台与安检通道最优距离分析

在排队方式为A2的前提下，分析验证服务台与安检通道的最优距离。旅客到达率分别选取402、623、802 人/h，对1～20 m 的距离，验证服务台每隔1 m 放置的情况，各进行20 次仿真，得到的平均单队列人数变化如图11 所示，安检平均服务时间变化如图12 所示。由于验证服务台与安检通道的距离越远，旅客此段路程耗费的时间越久，当验证服务台前提到20 m 时，按照设置的步速，旅客至少需要走30 s，接近平均服务时间的一半，因此，不再考虑20 m 以上的情况。

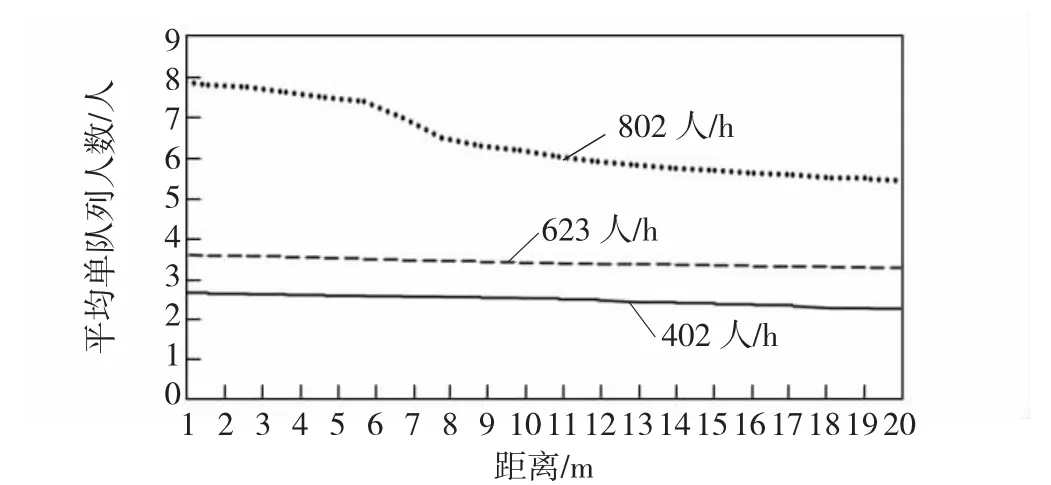
图11 平均单队列人数变化情况Fig.11 Change of average number of people in a single queue

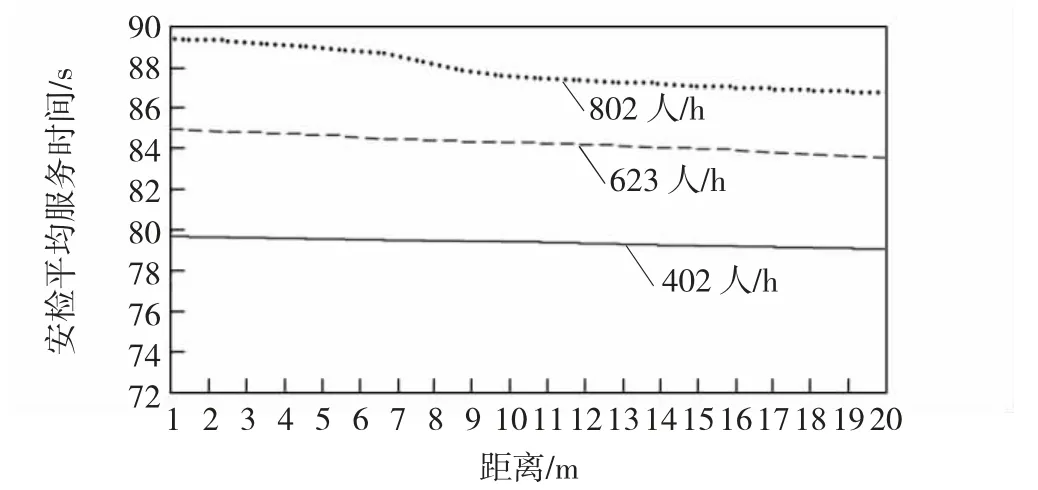
图12 安检平均服务时间变化情况Fig.12 Change of average service time of security check

由图11 和图12 得到，20 m 的距离平均单队列人数及安检平均服务时间的2 项性能指标表现更好。同时可以看到旅客高峰期802 人/h 时，在7 m 左右出现了平均单队列人数和安检平均服务时间骤降的情况，这是因为旅客到达人数过多，出现了排队现象，同时也导致安检平均服务时间较长，而验证服务台提前到7 m 左右时，缓解了在验证服务台处旅客堆积的情况。

因此，在排队方式为A2前提下，从平均单队列人数及安检平均服务时间考虑，选择验证服务台远离安检通道20 m 放置。

通过上述分析，发现1 对1 且验证服务台远离安检通道20 m 的排队方式表现效果最好，队列可采用S形，充分利用机场旅客安检验证服务台前的空间面积。同时可推测出验证服务台和安检通道的距离越长，安检效率越高。然而受机场安检空间的限制，并且如果验证服务台与安检通道距离过长，则旅客此段路程耗费时间过多且无法保证旅客在经过验证服务台后会直接走向安检通道进行安检，因此，此段距离不能无限大。在实际机场安检中，可根据现有空间，适当增大验证服务台与安检通道的距离，以此提高安检效率。

5 结语

为了探索旅客排队方式对机场安检效率的影响，本文利用AnyLogic 软件，结合排队论和社会力模型，根据机场安检实际情况建立6 种排队方式的机场旅客安检仿真模型，并输入实际数据运行模型，得到安检总时间、平均单队列人数、旅客平均等待时间和安检平均服务时间4 个性能指标，结合实际情况，对运行结果进行对比分析，得到最优排队方式为1 对1 且验证服务台远离安检通道放置的结论。

通过计算、对比和分析验证服务台远离安检通道1～20 m，每隔1 m 放置时的运行结果，得到验证服务台远离安检通道20 m 的效果更好。最终得出最优排队方式为1 对1 且验证服务台远离安检通道20 m 的结论。这种排队方式的队列长度比传统安检排队方式更短，旅客平均等待时间和安检平均服务时间的总计用时比其他5 种排队方式更短，可缓解验证服务台处的服务压力，从而提高安检效率。

未来的研究工作可以在本文的基础上，加入关于旅客风险分类的内容，随着机场及旅客对于安检效率需求的提高，旅客安检分类可能会成为一个未来的发展趋势。对旅客的风险分类，采取不同程度的安检措施进行安检，研究不同的排队方式是否会对安检性能产生影响。这可作为相关部门探索更多关于中国机场安检系统研究的参考。