曲线钢-混组合箱梁桥车桥耦合振动及支座受力研究

孙渤佳,马海龙,王荣霞,王东升

(1. 河北工业大学 土木与交通学院,天津 300401; 2. 河北首都新机场高速公路开发有限公司,河北 廊坊 065000)

0 引言

车辆通过桥梁时彼此的相互动力反应构成了车桥耦合振动问题[1]。关于车桥耦合振动,已有研究主要集中于直线梁桥[2-4],对曲线梁桥的研究相对较少。曲线梁桥与直线梁桥相比具有更加复杂的静力与动力反应形态:如在自重作用下其存在弯扭耦合效应,内、外侧支座受力不均并出现拉力,出现如“爬移”等无法预计的变形形式等。目前,一些主梁倾覆的案例中,曲线梁桥也占有相当大的比例[5-6]。当车辆在曲线梁桥上行驶时往往会加剧上述现象的发生,或者使之处于更不利的状态,某些时候会影响桥梁的正常使用[7]。因此,曲线梁桥的车桥耦合振动问题更加值得关注。

国内外学者对曲线梁桥的车桥耦合振动问题进行了现场试验以及有限元模拟,黄新艺等[8]、SENTHILVASAN等[9]、HUANG[10]分别针对曲线钢-混组合梁桥以及钢筋混凝土曲线梁桥进行了现场跑车试验,并利用有限元软件建立车桥耦合模型进行分析验证,研究表明一个合适的有限元力学模型可以很好地预测桥梁对动态荷载的响应。HUANG等[11-12]针对钢筋混凝土曲线梁桥提出车桥空间数学模型(space mathematical models)来确定车辆对桥梁动态响应的影响,其通过曲线薄壁梁单元对曲线梁进行数值离散,较其他方法减少了计算时间并且较容易得到桥梁的内力响应。晏路曼[13]、罗浩[14]基于ANSYS有限元软件以某座钢筋混凝土曲线梁桥为例建立车桥耦合振动模型,前者利用模态综合技术与Newmark-β两者相结合编制了求解曲线车桥耦合振动的响应程序,提高了计算的速度而后者利用Matlab编制曲线梁桥车桥耦合振动的程序,有效减少了计算时间。TAN等[15]将汽车以移动质量方式模拟为竖向力以及径向力,求得水平曲线梁桥在车桥耦合作用下的解析解,可一定程度验证数值解的准确性。在此基础上,部分学者通过ABAQUS有限元软件,基于Fortran语言将车辆荷载简化为移动力来计算冲击效应[16-18],并针对钢筋混凝土曲线梁桥[19-20]以及曲线钢-混组合梁桥[21]进行车桥耦合振动的模拟。需要指出,这种方法忽略了车桥耦合振动中车辆(含车辆惯性[22-24]以及车桥共振[25-26])的影响,其计算结果与实际状况有一定的出入。

近些年,受钢桥快速建设的驱动,以钢箱结合混凝土桥面板的钢-混组合箱梁桥的建设较多,也包含曲线梁桥。在设计中因对该桥型车桥耦合振动认识有限,相关支座受力变化和冲击系数取值等问题尚未解决,而在曲线梁桥设计中,支座是否会出现拉力及是否需要采取措施是必须考虑的。由此,本文采用ABAQUS软件,以某高速曲线钢-混组合箱梁桥为背景,发展了一套车桥耦合振动问题的数值模拟方法,在利用现有文献实测或模拟数据验证该方法正确性的基础上,分析了车辆在不同行驶半径(曲线梁内、外侧)和不同超高条件下支座竖向反力的变化。本文可为曲线钢-混组合箱梁桥车桥耦合振动的深入研究提供可行性的方案。

1 曲线梁桥车桥耦合振动分析方法

1.1 车辆运动方程

车辆建模为具有9个自由度的质量-弹簧-阻尼系统,分别为车轮、车体的竖向自由度δ={ZV,ZS1,ZS2,ZS3,ZS4,ZS5,ZS6,θ,Φ},车辆与路面接触点的位移与桥面的位移相同,因此该接触点不是独立的自由度。具体车辆模型如图1所示。

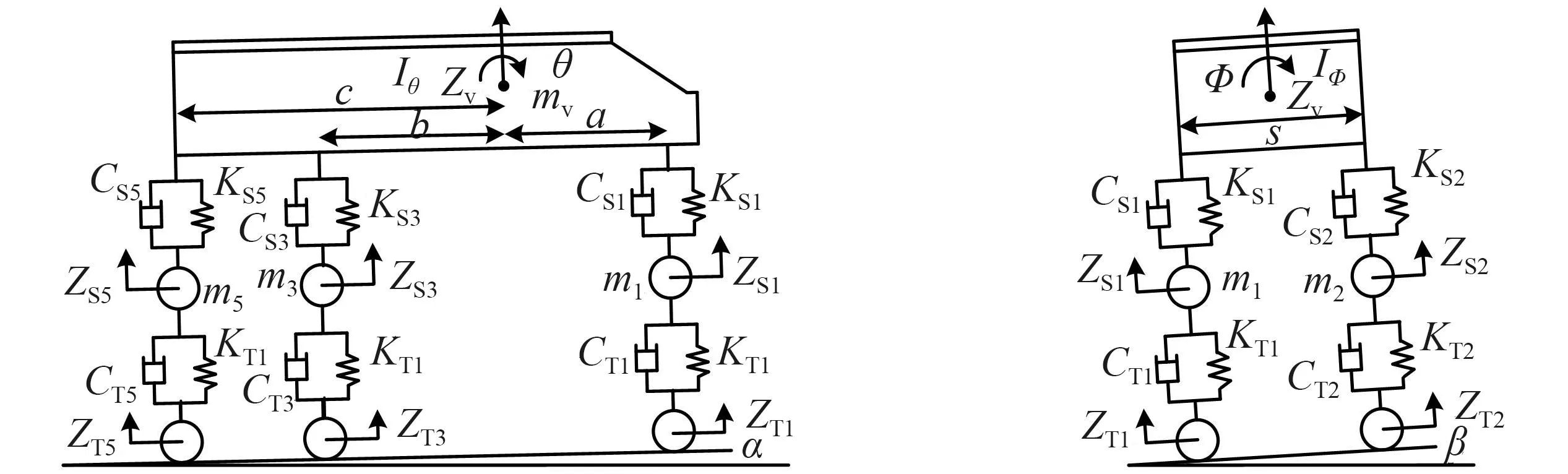
图1 计算车辆模型图Fig.1 Calculated vehicle model diagram

由图1可知,ZV为车体的竖向位移;ZSi为车轴处的竖向位移;a、b和c分别为前轴、中轴以及后轴到车体重心的距离;S为左右两车轴中心点的距离;KSi为悬架系统的刚度系数;CSi为悬架系统的阻尼系数;KTi为车轴与轮胎连接弹簧的刚度系数;CTi为车轴与轮胎连弹簧的阻尼系数;θ为车辆的俯仰角度;Φ为车辆的侧倾角度;mV为车体的质量;mi分别为各个车轴的质量;ZTi为轮胎处的竖向位移;Iθ为车辆的俯仰惯性矩;IΦ为车辆的侧倾惯性矩。其中i=1,2,3,4,5,6。

本文根据达朗贝尔原理推导三轴九自由度车辆的振动方程,其中车体的竖向位移、俯仰、侧倾以及车轴的竖向位移的平衡方程为

(1)

(2)

(3)

(4)

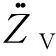
其中每个车体与悬架系统弹簧连接处的位移ZV,通过式(5)计算得

(5)

式中参数物理含义已经在文中介绍。

通过式(1)～式(5)可整理得出车辆振动的矩阵方程为

(6)

1.2 桥梁运动方程

对于桥梁的运动方程为

(7)

1.3 车桥相互作用方程

根据车桥接触点的位移关系与作用力关系可以建立如式(8)的方程[27]:

(8)

式中:Cb-b、Cb-v和Cv-b为车桥相互作用的阻尼耗能项;Kb-b、Kb-v和Kv-b为相互作用的刚度;Fb-v和Fv-b为车桥之间的相互作用力;其余参数同前面介绍。

当已知任意时刻的车轮及接触点的位移及速度,相互作用力公式为

(9)

式中:ZT为车轮处的竖向位移;dv为轮胎与桥梁接触点处桥梁的竖向位移;K,C分别为与地面接触时轮胎的刚度与阻尼。

1.4 车桥耦合运动方法

在本文研究中,首先基于ABAQUS有限元软件建立车桥耦合振动模型,之后采用内嵌的Hilber-Hughes-Taylor-α(HHT-α)隐式动力方法将车辆和桥梁的振动进行耦合并迭代求解。该方法是由Hilber、Hughes和Taylor引入自由参数α并以Newmark-β的方法为基础发展起来的[28],具有参数单一,数值阻尼可控,可消除由于改变时间步长而引入的小高频噪声等优点。为实现车辆的曲线运动[29],可将车辆运动分解为x与y方向的三角函数运动,如图2所示,事实上周期型幅值广义上都可采用傅里叶级数表示为

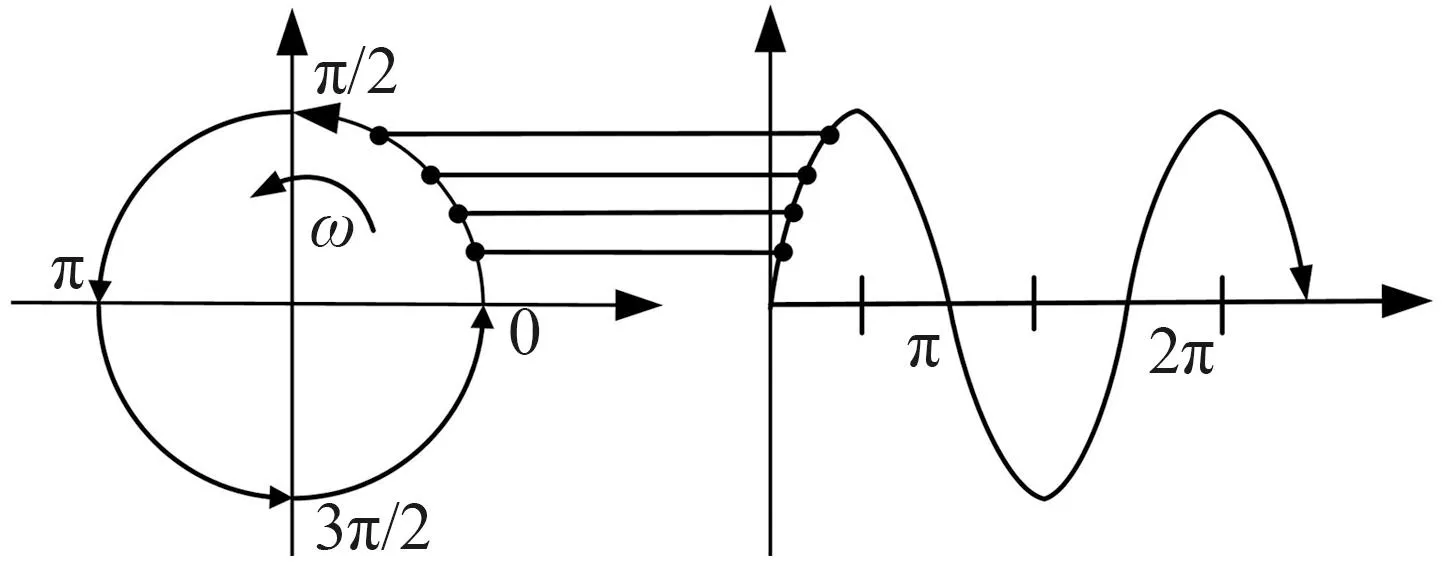
图2 转动与正弦函数的对应关系Fig.2 Corresponding relationship between the rotation and the sine function

(10)

式中:An与Bn分别为cos项与sin项的系数,与初始位置x与y的数值相关;N为傅里叶级数项的个数,对本文的圆曲线运动,取为1;ω为圆频率(rad/s),通过车辆的行驶时间和距离进行计算;A0为初始幅值,其大小与行车曲率半径相关;t0为初始时间,本文中取值为0。

车轮与桥面采用面与面接触,接触属性采用无摩擦的切向行为与罚函数的法向行为。前轮、中轮与后轮之间以及车体内部采用转换器单元连接。在ABAQUS中建立局部坐标系,因此转换器在局部坐标系中仅在车辆竖向方向存在位移的自由度,限制住了其他方向位移及旋转的自由度,如图3所示。

图3 转换器连接件原理图Fig.3 Schematic diagram of converter connectors

2 车桥耦合振动数值方法验证

本文基于ABAQUS有限元软件,以某五跨连续梁桥[30]以及某跨线桥[8]为例,建立曲线梁桥模型并引入质量-弹簧-阻尼系统的实体车辆模型,利用傅里叶级数方法实现车辆的曲线运动,进行车桥耦合振动的数值模拟。通过与这些既有桥梁实测或数值结果进行对比,以验证本文建议方法的可行性。

2.1 对某5跨连续梁桥的分析

当车辆行驶于曲线梁桥上时,因车辆存在离心力,加之车辆(竖载)与桥梁的弯扭耦合作用,车辆对桥梁产生横向力,进而桥梁产生横向位移。在横向力作用下,易出现横向滑移、支座脱空和主梁侧翻等病害,因此横向位移在曲线梁桥车桥耦合分析中较为重要[31-32]。为验证该方法对于桥梁横向位移计算的正确性,以某5跨连续梁桥为例建立模型。该桥梁总长度为125.6 m,曲率半径R=160 m。桥段为单箱单室箱梁桥,材料属性及支座约束条件等可参考文献[33]。

采用工况为35 t的三轴车辆[34],以30 km/h的速度在光滑路面上行驶。提取第二跨箱梁底部中点数据,如图4所示,车桥耦合振动分析的结果也几乎相同。

图4 某5跨连续梁桥横向位移反应Fig.4 Transverse displacement response of continuous beam bridge with five spans

2.2 对某跨线桥的分析

以一座跨线桥为例建立模型[8],该桥段为单箱双室预应力混凝土箱梁,在上部铺设有4 cm厚的沥青混凝土。车行道宽为11 m,两侧分别设有0.5 m的人行道与防撞墙,路面存在6%的横向坡度,跨径布置:30 m+40 m+30 m,曲率半径R=280 m。仅模拟上部结构,对于支座采用固定约束。

工况为30.4 t的三轴车[35],以30.4 km/h的速度沿着外侧偏心1.8 m处行驶。车辆在光滑路面行驶过程中在第一跨跨中的位移动力响应结果如图5所示,本文计算结果也与文献[8]实测结果较为一致。

由图4和图5可知,在ABAQUS中发展的车桥耦合振动模拟计算结果与文献[8,30]的实测和有限元结果具有很好的一致性,充分说明了本文方法的正确性,因其是基于通用有限元软件ABAQUS实现,故具有更好的可操作性。

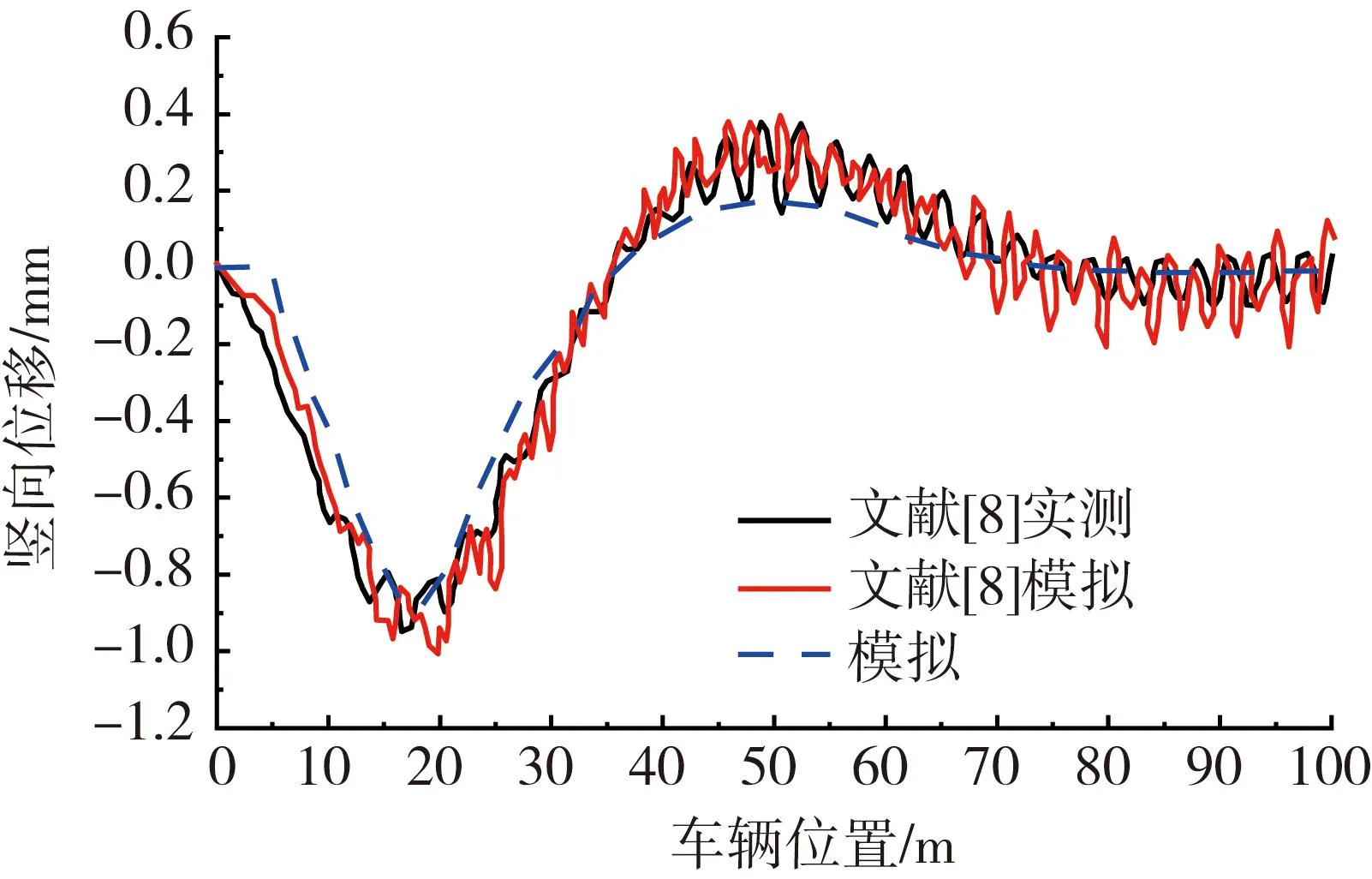
图5 某跨线桥加载侧竖向反应Fig.5 Vertical respense on the loading side of the flyover

3 曲线钢-混组合箱梁桥车桥耦合振动分析

3.1 工程概况

以某高速曲线钢-混组合箱梁桥为例,其横截面及跨径如图6所示。采用ABAQUS有限元软件建立空间桥梁模型。桥梁跨径布置为:27 m+2×43 m+27 m,曲率半径R=160 m,桥面铺装层:10 cm厚的沥青混凝土+防水层+8 cm厚的C50混凝土,桥面荷载:公路-1级,桥面宽10.5 m。支座分别采用1#至4#表示该桥段为双箱单室钢箱梁,边界约束条件依空间支座的布置情况施加在箱梁底板处,即不考虑墩柱对上部结构的影响[36],如图6所示。分析中桥梁阻尼采用瑞利阻尼假设[37],箱梁与箱间横梁材料为Q345qD钢,桥面板材料为C50混凝土,铺装层由沥青混凝土与C50混凝土组成,具体材料参数如表1所示。

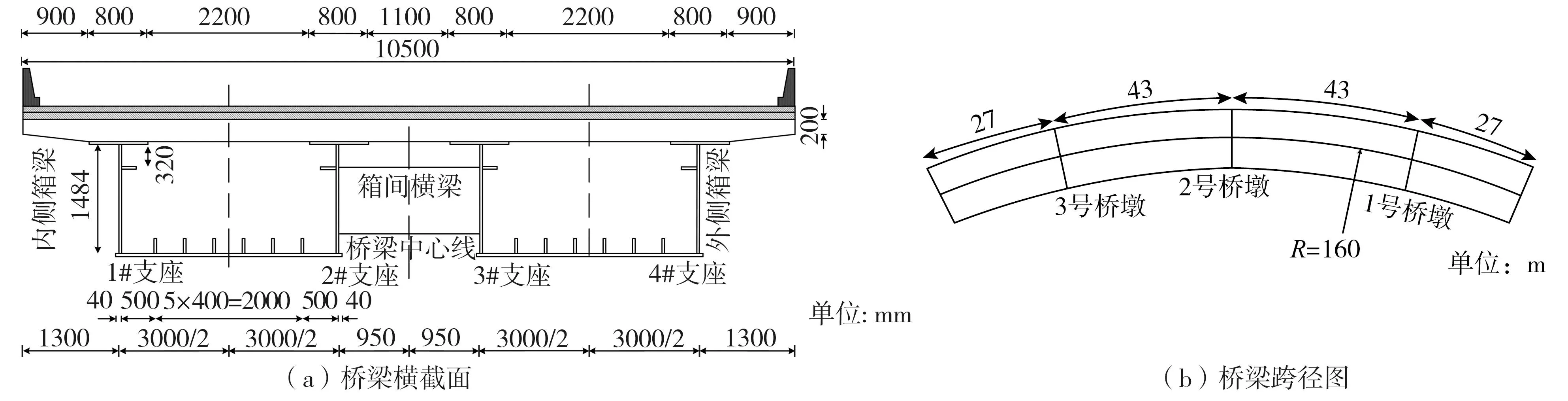
图6 曲线梁桥模型Fig.6 Curved bridge model

表1 曲线桥材料参数Table 1 Material parameters of curved bridge

桥梁上部结构采用空间支座约束,连续曲梁的支座布置如图7所示。

图7 连续曲梁支座布置Fig.7 Layout of continuous curved beam support

该桥现场试验采用脉动法进行自振频率测试,并对桥梁试验测得的振动加速度时程做FFT变换得到桥梁的前3阶振动频率,与数值模型的前3阶频率进行对比,结果如表2所示。

表2 前3阶实测频率与模拟频率Table 2 The first three measured frequencies and simulated frequencies

由表2可知,有限元模型计算的前3阶固有频率与该曲线桥的实测频率接近,误差最大为8.59%,说明有限元计算模型的质量、刚度和约束条件总体上接近于实际桥梁结构。

本文采用的车辆为三轴货车,重17.8 t,在车辆运动过程中假设车轮始终接触地面运动,并且车体在运动过程中不发生变形[14,38],车辆轮胎接地面积采用0.4 m×0.2 m。车辆参数如表3所示。为更好的模拟实际跑车的工况,分别在驶进桥梁前与驶出桥梁后假设存在一定的曲线路面段,其不被纳入到车桥耦合振动模拟结果,仅是为了满足模拟的物理边界。

表3 模拟车辆参数[34]Table 3 Simulation of vehicle parameters[34]

当车辆与桥梁发生耦合运动时,时间增量步Δt的选取尤为重要,时间增量步Δt与桥梁竖向振动周期T存在Δt≤0.1T关系时,认为模拟的结果较为良好[39]。由表4已知,桥梁周期T≈0.4 s,因此综合考虑计算的时间成本及精度将时间增量步Δt设为0.02 s。

动力荷载下简支梁桥及连续梁桥中支座反应行为已有一定研究[40-41],但曲线钢混组合箱梁桥行驶车辆对支座的影响尚缺乏。因此,本文分析了车辆行驶位置半径、桥梁超高对曲线梁桥2号桥墩内外侧(1#支座～4#支座)支座受力的影响(图6),并假设支座为刚体(未考虑弹性及破坏效应)。

3.2 车辆行驶半径对支座受力的影响

由于桥梁存在曲率的影响,使得车辆是否沿着中心线行驶,都会存在弯扭耦合现象,使内、外侧的腹板受力不均,进而导致支座受力的改变。对于车辆行驶位置的研究,曲线工字梁桥的成果尚有些参考[42-43],但曲线箱梁桥的成果主要集中于单箱梁桥[44],对于本文双箱梁桥的研究尚未见到。

因此本小节考虑5种行车位置,分别沿着半径R为156、158、160、162、164 m,如图8所示,以50 km/h的速度行驶,计算2号桥墩内外侧支座的竖向支座反力,如图9所示。并计算车辆以30、50、70、90 km/h的速度行驶条件下2号桥墩内外侧支座竖向支座峰值反力,计算结果如表4所示。

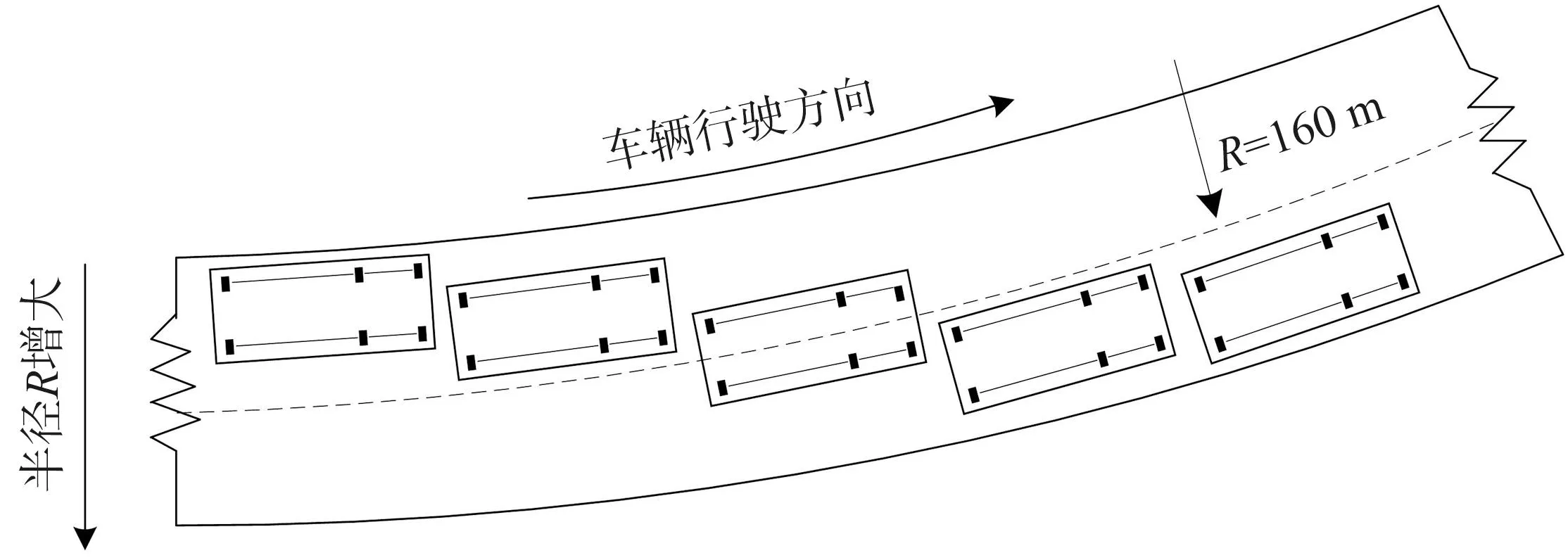
图8 车辆行驶半径Fig.8 Radius of driving vehicles

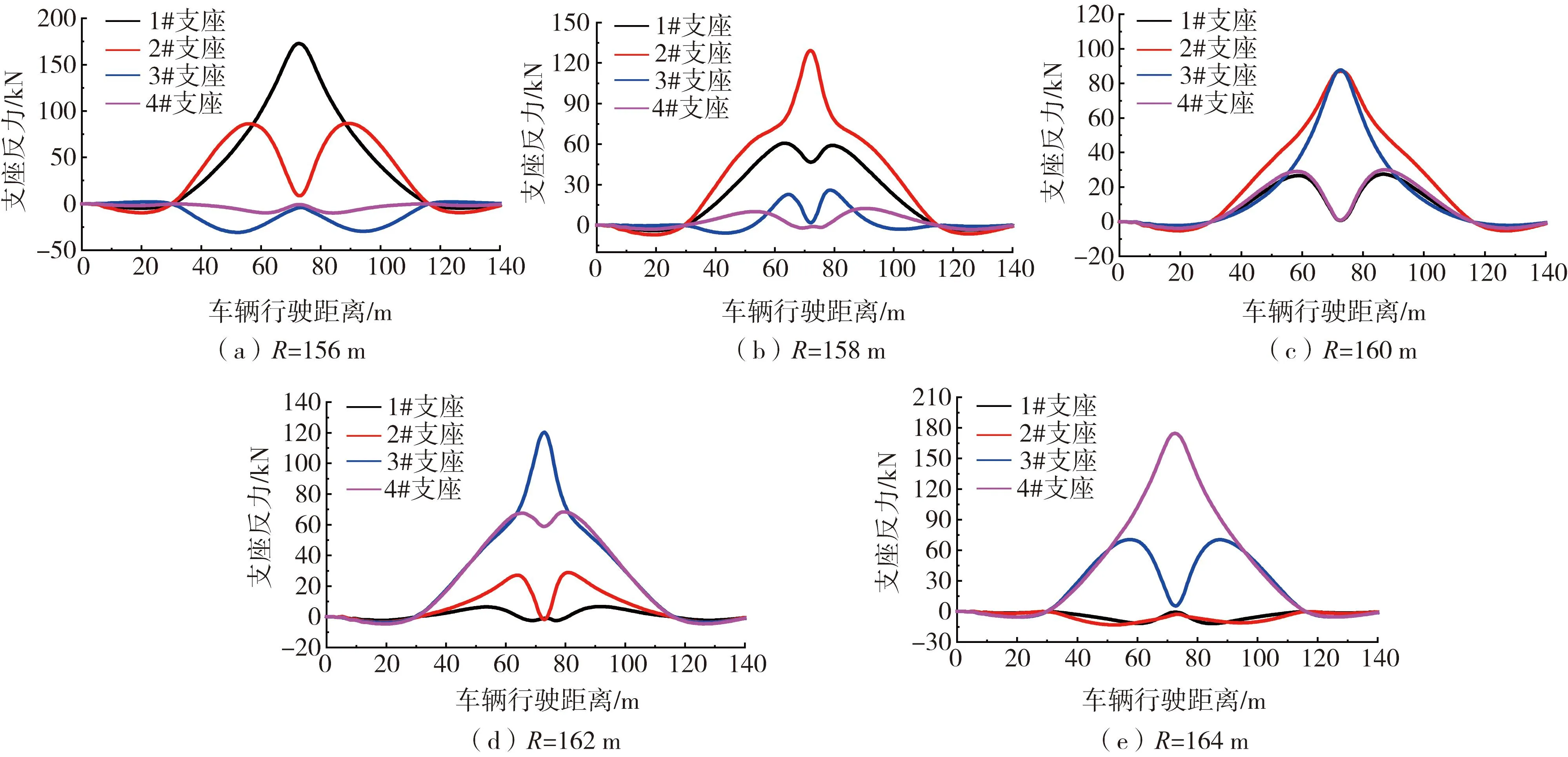
图9 内外侧支座受力Fig.9 Reaction force of inside and outside supports

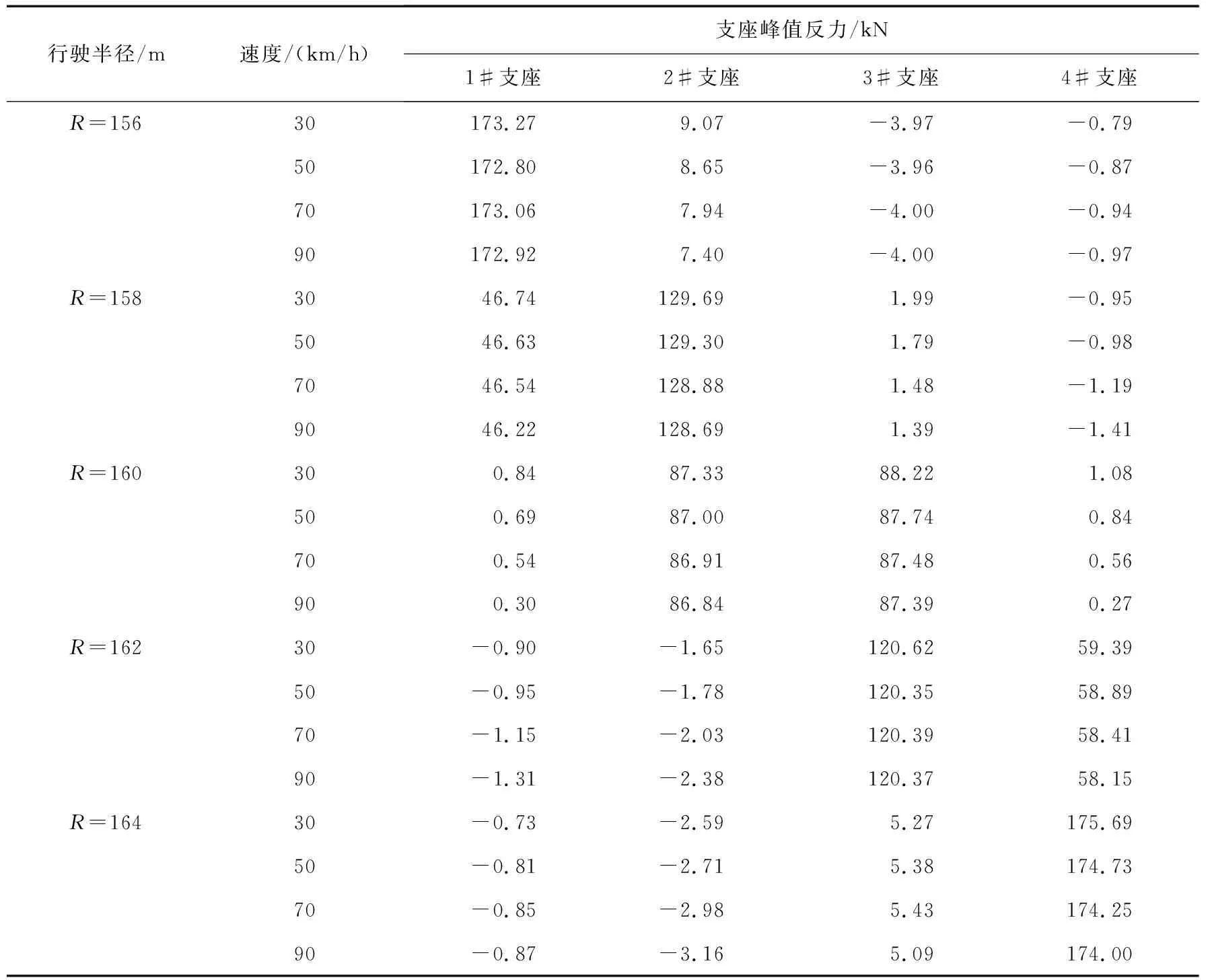
表4 内外侧支座峰值反力Table 4 Peak reaction force of inside and outside supports

当车辆沿着R=156 m路径行驶时,3#支座和4#支座处于拉力状态即支座脱空,如图9(a)所示。曲线梁桥存在弯扭耦合作用,当车辆沿着半径R=156 m行驶时,存在桥梁向内扭转的趋势,使得外侧箱梁内侧(3#支座)的支座受到的拉力较大。当车辆行驶过程中1#支座反力先增大后减小,而2#支座反力呈现M形走势,在车辆行驶于2号桥墩时,2#支座反力迅速减小,主要承载力由1#支座承担,同样车辆沿着R=164 m路径行驶时外侧箱梁支座反力具有相同的趋势,如图9(e)所示。

当车辆沿着R=158 m路径行驶时3#和4#的支座脱空现象得到缓解,如图9(b)所示。同理车辆沿着外侧路径行驶时,存在桥梁向外扭转的趋势,使得内侧箱梁内侧(2#支座)的支座受到的拉力较大。1#支座的反力呈现M形走势,而2#支座反力先增大后减小,主要承载力由2#支座承担。同样车辆沿着R=162 m路径行驶时外侧箱梁支座反力具有相同的趋势,如图9(d)所示。因此当车辆在内侧或外侧行驶时,会发生支座脱空及单支座承担荷载的现象,这是一种非常危险的现象,应得到重视。

当车辆的行驶速度逐渐增大时,受拉支座的峰值反力的逐渐增大,受压支座的峰值反力具有减小的趋势。因此降低车辆行驶速度可以减轻支座脱空,但支座峰值反力的变化微乎其微,如表4所示。

3.3 桥梁超高对支座受力的影响

当车辆在曲线梁桥行驶时,与桥梁之间存在沿径向的摩擦力。为了防止车辆高速行驶时发生过大的侧向偏移及发生“侧向打滑”,曲线梁桥会设计为外侧高内侧低的具有一定超高的截面形式[43]。因此本文考虑了2种截面,分别为无超高以及6%的超高,如图10所示。

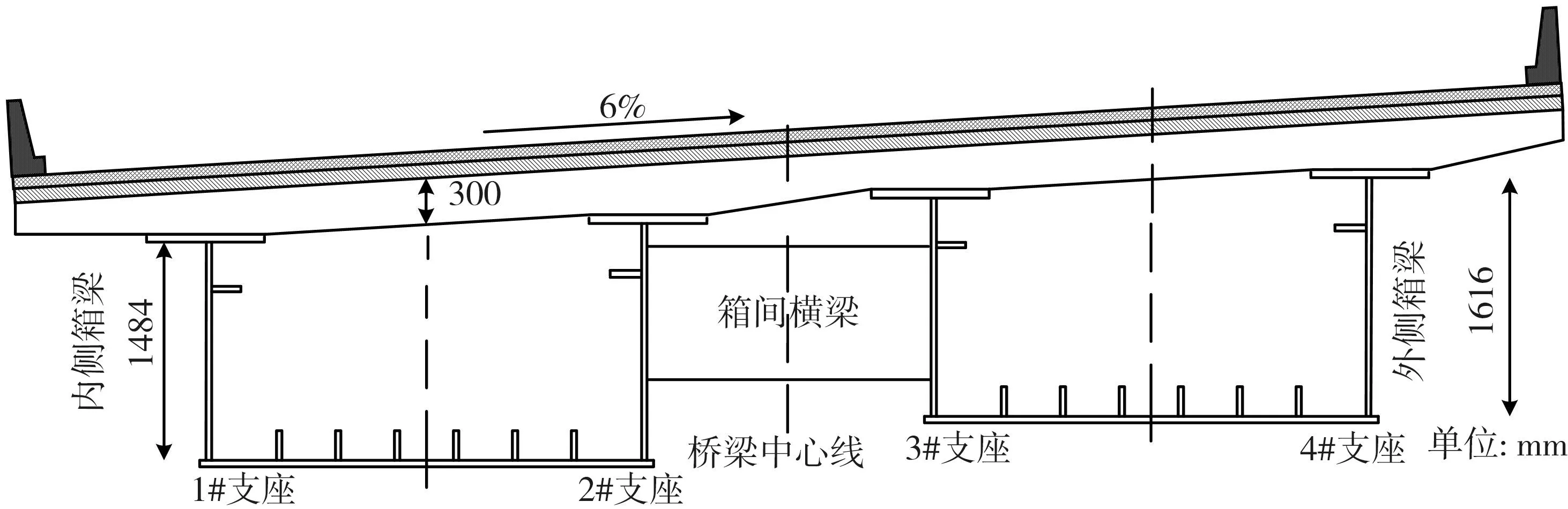
图10 6%超高截面形式Fig.10 Section form of 6% super elevation

由上一节的结论可知,车辆行驶速度对于支座峰值反力的影响较小,因此本节不再考虑车速的影响。使车辆以50 km/h的速度沿着R为156、158、160、162、164 m这5种路径行驶,分别计算2号桥墩处内外侧支座的竖向支座反力及支座峰值反力,计算结果如图11及表5所示。

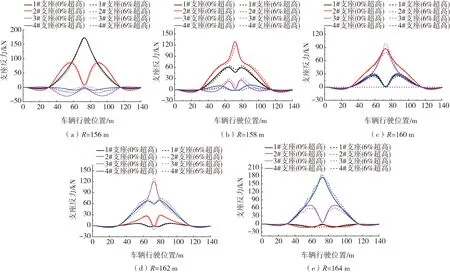
图11 不同超高条件下内外侧支座受力Fig.11 Reaction force of inside and outside supports under different super elevation

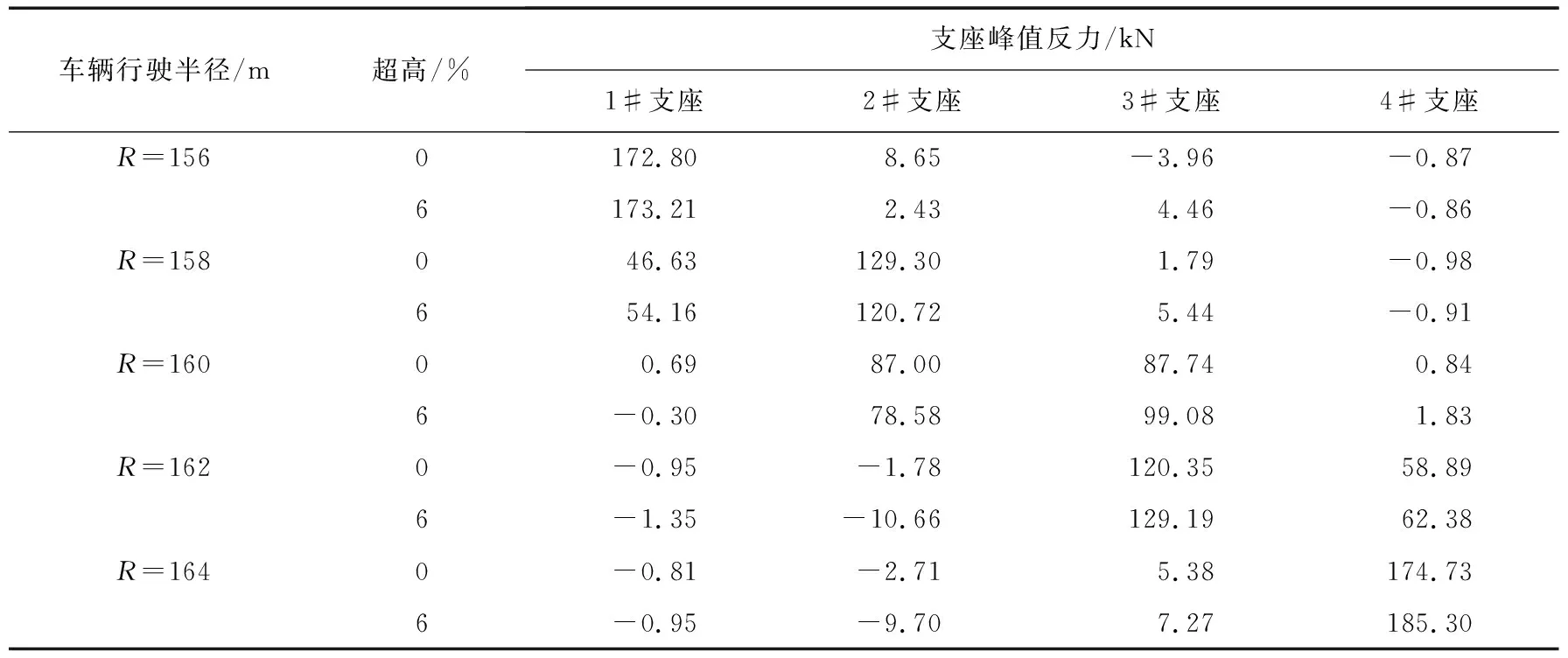
表5 不同超高条件下支座峰值反力Table 5 Peak reaction force of inside and outside supports under different super elevation

由图11及表5可知,尽管超高对支座反力有所影响,但变化的绝对值并不大。当车辆沿着内侧车道行驶并存在超高时,内侧箱梁的1#支座竖向反力增大,2#支座反力减小且外侧箱梁3#支座脱空现象得到缓解,但对4#支座竖向反力的影响较小。当车辆沿着外侧车道行驶时,随着超高的增加,增大了桥梁的弯扭耦合效应,使内侧箱梁支座拉力增加,加重了支座脱空现象。

4 结论

本文基于ABAQUS有限元软件,利用傅里叶级数模拟车辆平曲线和竖曲线运动,实现了曲线钢-混组合箱梁桥车桥耦合振动分析。以某高速曲线钢-混组合箱梁桥为例,研究了车辆在内外车道以不同速度行驶及超高条件下对桥梁支座反力的影响,并得出如下结论:

1)曲线梁桥车桥耦合振动数值模拟方法基于有限元软件ABAQUS实现,具有更好的通用性和可操作性。

2)车桥耦合振动数值模拟可获得支座受力变化的全过程,就算例桥梁,当车辆分别在曲线梁桥内侧和外侧行驶时,都会使另一侧箱梁的最外支座出现脱空。

3)6%的桥梁超高对支座受力影响的绝对值变化值不大;但当车辆沿曲线内侧车道行驶时,超高可缓解部分支座脱空;当车辆沿曲线外侧车道行驶时,它会加重了某些支座脱空。

4)车辆的行驶速度对于支座峰值反力的影响微乎其微,但可以通过降低车速进而减轻支座脱空。

5)本文将支座假设为刚体,未研究支座弹性反应及(自身)破坏行为。后续工作将分析车重、路面不平度以及伸缩缝等参数对支座受力行为的影响,将对支座细节建模进行研究,以充分考虑行车对曲线梁桥的动力影响,以期为车桥耦合振动条件下支座设计,还有增强曲线梁桥的抗倾覆能力等提供工程参考。