基于实测波浪的单桩式海上风电基础波浪力计算研究

朱民涛，宋 虹，周 胡，和法利，刘福顺，常 爽

（1.中国海洋大学 工程学院，山东 青岛 266100；2.浙江省深远海风电技术研究重点实验室，浙江 杭州 310014；3.中电建华东勘测设计研究院有限公司，浙江 杭州 311122；4.中国绿发江苏广恒新能源有限公司，江苏 南京 210000）

近年来海上风能技术发展迅速，海上风机装机容量也与日俱增，环境荷载的准确计算对海上风电的安全、高效运营至关重要。在未来的5～10年内，随着风机进入服役的中后期，海上风电开发重心也将逐步由大规模建设向安全运维转移。波浪荷载的获取作为实测环境下的结构物动力响应分析以及数字孪生模型建立的必备环节，是海上风电数字化运维发展过程中不可回避的重要问题。海上风电单桩基础作为典型的海工结构形式，依据DNV 规范［1］，其波浪荷载计算在桩基直径与波长的尺度因子D/L＜0.2 时采用Morison 方程［2］，在D/L＞0.2时采用绕射理论［3］。在结构物的设计阶段，通常采用累计频率法计算某个特征波的波浪力即可完成结构物的强度校核，然而相对于设计阶段采用的设计波，实测波面均为非规则波，其尺度因子D/L难以采用某一确定的数值衡量，导致波浪荷载计算方法的选择缺乏理论指导。因此，研究实测波浪作用下海上风电基础波浪力计算方法，对海上风电数字化运维有重要的指导意义和参考价值。

自Morison 方程和绕射理论提出以来，学者对他们的改进与修正从未间断，力求使其更适用于特定工况。陈凌等［4］通过OpenFOAM 求解Euler 方程和N-S 方程详细探讨了黏性力和惯性力随圆柱尺度比变化的规律，给出了各自表现显著的区间；同时，提出了中等尺度的概念，给出了不同尺度结构的波浪力计算方法。刘梅梅等［5］通过物理模型试验的方法分析了上窄下宽的复合塔筒反弧段上的波浪荷载随水动力参数的变化规律，指出了分析复合塔筒波浪力时波浪力计算方法不能统一而论，Morison 方程和绕射理论各有其适用工况。胡勇等［6］对桩柱波浪力计算现状进行了归纳总结，结合已建跨海大桥的工程实践，通过模型试验结果与现行规范所得结果进行对比，提出了特定工况下波浪力计算存在的问题以及解决方案。周远洲等［7］基于Morison 方程、边界元、CFD 方法计算了桥梁基础在D/L= 0.2 左右的波浪荷载，结果表明Morison 方程高估了拖曳力的贡献，边界元方法和CFD 方法吻合较好。这些研究虽然阐述了Morison 方程和绕射理论在特定工况下的适用性，但是均停留在规则波阶段。

由于海上风浪随机性较强，一段时间内的波浪难以以某一特定的波高周期参数衡量，此时通常采用波浪在一定时间内的统计特征计算尺度因子，在此基础上结合线性叠加原理来确定波浪力的计算方法。Tanaka等［8］对Spar平台的动力分析中采用Morison方程由实测波面求解波浪力时程，其水动力系数的选取以小时为单位，通过统计每个小时的谱峰周期和有效波高计算得到，这之后将此水动力系数作用在所有波浪成分上。Sun 和Jahangiri［9］、樊惠燕［10］对5 MW 固定式风机进行结构动力分析时，采用线性叠加法分别通过JONSWAP 谱或P-M 谱求解波面与水质点速度，之后采用Morison 方程求解不规则波波浪力。张胡等［11］采用边界元法建立了大尺度结构所受波浪力的数学模型，通过对比实测桥墩波浪力数据验证了该模型的准确性。虽然有效波高和有效周期等特征值能反映出不规则波的主要组分特性，但是对波浪力进行计算难免会忽略其他波浪组分的影响，从而造成波浪力计算结果的偏差。

首先采用CFD 方法生成不规则波面时程，并基于此运用不同波浪计算方法计算不规则波作用在单桩基础上的波浪力；通过计算结果与数值模拟结果的对比探讨不规则波作用下Morison 方程和绕射理论关于尺度因子的适用范围，并基于此进一步针对海上实测波面数据进行分析；通过计算典型海况下的波浪力特征以期为实际服役风机波浪力计算提供技术支持。

1 不规则波波浪力的计算

波浪力在工程中难以直接测量，因此这里采用实测波面推知结构所受波浪荷载。首先将实测波面进行分解，依据波浪理论计算各成分波浪要素，分别采用两种波浪力计算方法对单桩基础的波浪荷载进行求解。

1.1 波浪理论

根据线性叠加原理，线性不规则波可以被看作是有限个不同振幅、不同周期、不同初始相位的规则波叠加而成［12］，即：

其中，Ai、ωi、δi分别表示组成该不规则波分量的第i个规则波成分的幅值、频率和初始相位。

对于某个特定的波浪成分Φi，根据Airy波理论，由速度势函数可以导出波浪水质点的运动特征，其水平速度和水平加速度为：

1.2 Morison方程

Morison 方程适用于小尺度构件，Morison 方程的适用范围要求截面尺寸D和波长L的比值较小，一般要求D/L＜0.2，它包含黏性项和惯性项两项，其中黏性项是按照黏性流体分析得到，惯性项是通过势流理论计算得到。对于小尺寸的竖直圆柱，某个波浪成分对任意高度z处单位长度的水平波浪力可以通过Morison 方程表示为：

式中：fD，i为拖曳力；fI，i为惯性力；CD为拖曳力系数；Cm为附加质量系数；CM= 1 +Cm为惯性力系数；ρ为海水密度；A为垂直于波浪传播方向的单位柱体高度的投影面积；V0为单位柱高的排水体积；D为圆柱直径。

Morison方程作为半经验公式，其波浪力计算的精度取决于水动力系数CD、CM的选择。对于计算海上风机基础结构，一般具有较大的雷诺数（Re＞1 × 106）和较小的KC 数（KC＜0.5），同时钢制结构表面也较为光滑（Δ/D＜0.000 1，Δ为取样长度内轮廓偏距绝对值的算术平均值），此时CD、CM都趋于一个定值，根据Sarpkaya 等［13］的建议可取CD= 0.62、CM= 2.0；根据DNV 设计规范［1］计算可得CD= 0.5、CM= 2.0。这里计算时取CD= 0.5、CM= 2.0，事实上当KC＜5时，拖曳力项的影响忽略不计［14］。

1.3 绕射理论

绕射理论适用于大尺度构件，工程上一般要求截面尺寸与波长的比值D/L＞0.2。根据线性绕射理论，第i个波浪成分对高度为z的单位柱高圆柱造成的顺向波浪力为：

其中，

式中：a为圆柱半径；Jl(kia)和Nl(kia)分别是变量为kia的一阶第一类Bessel函数和第二类Bessel函数。

2 数值模拟

前文阐述了基于实测波面的波浪力计算方法，其针对实际工况的适用性尚未可知，因此，以OpenFOAM（open field operation and manipulation）数值模拟结果为基准，验证前文所述2 种波浪力计算方法的准确性。模拟中使用有限体积法对控制方程进行离散，其中控制方程的时间项采用Euler格式，对流项和扩散项均采用二阶中心差分格式，涡黏性系数采用k-ω SST 模型来等效，其k与ω均采用二阶迎风格式。采用PIMPLE（PISO-SIMPLE）算法实现对压力场、速度场的解耦运算。波浪的产生使用开源工具箱waves2Foam 进行模拟，通过松弛区造波、消波法修正计算域的波浪高程、压力、速度分布。

2.1 数值模型准确性验证

为了验证数值模拟波浪场的准确性，对Mo等［15］的波浪与竖直圆柱相互作用的试验进行模拟，并进行了结果对比。选取水深4.76 m、周期4 s、波高1.2 m 的工况进行模拟，建立的数值水槽为90 m×7 m（长×宽），圆柱直径0.7 m，圆柱中心距离入口50 m，具体布置及边界条件设置如图1 所示。圆柱前方、侧方、后方布置3个虚拟波高仪，在水槽侧壁布置1个虚拟波高仪作为对照。

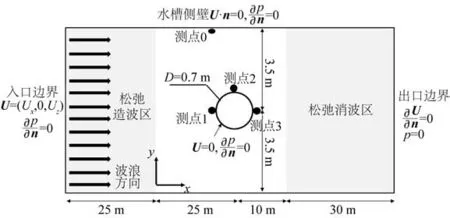
图1 数值水槽布置及边界条件设置Fig.1 The numerical tank layout and boundary condition settings

计算结果的波高使用0 号波高仪测得的最大波高进行无量纲化处理，时间通过波浪周期T进行无量纲化处理。计算得到的波浪力和波面如图2、图3 所示，其中，ηWGn为各测点的波面时程，ηmax，WG0为0 号测点的波高最大值。

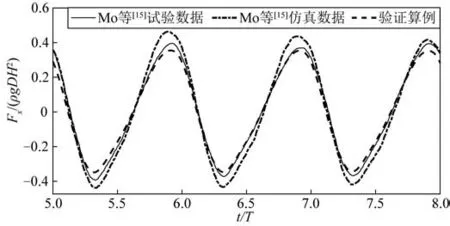
图2 水平波浪力时历曲线Fig.2 Time history of horizontal wave forces

图3 波高时历曲线Fig.3 Time history of surface elevation

从图2和3中可以看出，计算结果与Mo等［15］的试验符合良好，为了进一步衡量两条曲线的吻合程度，用拟合优度R2来量化评估，如式（8）所示。

式中：fr为参考的数据；fv为待评估的数据；-fr为参考数据的均值；n为数据长度。

如表1 所示，分别给出Mo 等［15］的算例结果及数值模拟结果与试验结果的拟合优度。由表1 可知，数值模拟结果与试验结果重合度高，且精度高于Mo 等［15］的模拟结果，由此证明了这里采取的数值模型的可靠性。

表1 Mo等[15]算例与验证算例结果对比Tab.1 The comparation between Mo’s simulation and validated simulation

2.2 网格收敛性与时间步长收敛性验证

网格和时间步长的大小对数值模拟的计算精度和计算效率有着关键影响。为了选取合适的网格和时间步长，参照江苏如东某风场的4 MW风机基础实际尺寸与实际海况（桩基直径5.5 m，设计高潮位9.75 m，平静海况谱峰周期TP= 5.0 s，有效波高HS= 0.5 m），采用6 组网格和时间步长组合对该海况的波面进行模拟，网格尺寸和时间步长组合如表2 所示，其中组合1 为2.1 节工况的网格尺寸，不规则波的模拟需要更加精细的网格尺寸［16］。

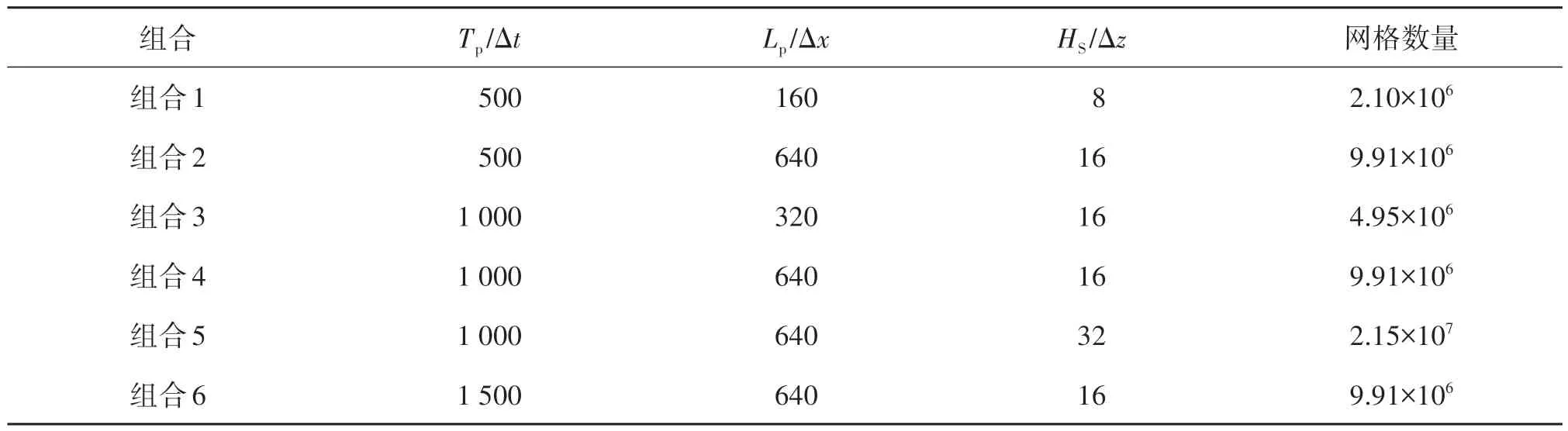
表2 网格与时间步长设置Tab.2 Settings of mesh size and time-step

图4为不同网格尺寸、不同时间步长下数值模拟波浪频谱与JONSWAP谱的对比。

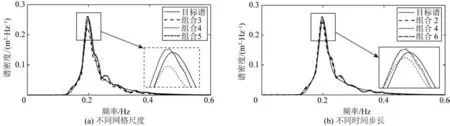
图4 数值波谱和目标波谱的对比Fig.4 The comparison of numerical and target wave spectrum

从图4（a）中可以看出：组合3的峰值偏低，说明网格配置精度不够，存在较大的数值耗散；组合4和组合5的网格精度满足要求。在时间步长方面，从图4（b）中可以看出：组合2的峰值较低，而组合4和组合6的频谱都与目标谱符合良好。此外，无论何种网格配置都存在波浪谱高频衰减问题［17］，这是由波浪的弥散关系决定的，波长近似与波浪周期的平方成正比，所以高频波浪分量的波长急剧减小，因此对高频的波浪进行精确的模拟需要非常精细的网格。但是从整体上来看，高频波浪的能量较小，对计算的结果影响较小，并且精细的网格和时间步长带来计算成本的指数上升，因此综合考虑计算效率和计算精度，这里选取组合4的网格划分和时间步长组合进行数值模拟。

依据组合4 中的网格划分形式建立的数值水槽如图5 所示，数值水槽尺寸为140 m×50 m×11 m（长×宽×高），圆柱中心距离入口70 m。数值水槽网格主尺度为0.5 m×0.5 m×0.25 m，并在水面以及圆柱周围局部加密，加密区域网格密度达到Δx= Δy=Lp/640，Δz=HS/16，圆周内单层260 个网格，第一层网格高度设置0.002 m。入口处设置一倍波长的消波区，出口处设置1.4倍波长的消波区，并且出口处的消波区间距逐渐放大，在松弛区消波的基础上增加数值耗散，以此增加消波能力以及减少网格数量。

图5 数值水槽网格划分Fig.5 The mesh generation of numerical wave tank

2.3 工况选择

海上风机基础的几何尺寸和所处海况均会影响其波浪荷载计算，因此，这里参照实际尺寸与实际海况，选取了桩基直径、谱峰周期和有效波高3组变量进行探讨，如表3所示。

表3 数值模拟采用的工况设置Tab.3 The setting of working conditions used in numerical simulation

其中：工况1-1～1-13 与工况3-1～3-6 主要通过改变周期与直径探究不同尺度因子的影响；工况2-1～2-6、3-1～3-6、6-1～6-6探究相同尺度因子下谱峰周期的影响；工况3-1～3-6、4-1～4-6、5-1～5-6探究相同尺度因子下有效波高的影响。

3 结果分析

基于OpenFOAM 数值模拟得到的波面时程，分别采用Morison 方程和绕射理论进行海上风电基础波浪力的重构，并以数值模拟得到的结构所受波浪力为基准，对Morison 方程和绕射理论的计算结果进行对比分析，以探讨不规则波作用下不同计算方法的适用性。

3.1 波面重构结果分析

准确的波面重构是进行波浪荷载计算的前提，以工况3-4为例，在测得未放置圆柱时圆柱中心位置的波面后，由快速傅里叶变换得到波面的频谱和相位谱，依据式（1）不规则波的分解，综合考虑计算效率和计算精度，取0.33ωp＜ωi＜3ωp的波浪分量进行计算，其中ωp为谱峰频率。

数值模拟得到的原始波面和重构后的波面如图6所示，图6（a）为100个谱峰周期的波高时程，图6（b）为60～100 s的波高时程。由图6可知：重构波高时程基本可以重现数值模拟结果，由此证明了这里采取的不规则波分解及重构方法的可靠性。此外，准确的波面重构为后续波浪力的准确求解提供了可信的输入。

图6 数值模拟波面和重构波面的对比Fig.6 The comparison between numerical simulation and reconstructed surface elevation

3.2 Morison方程与绕射理论结果对比

规范中通常依据尺度因子来选取Morison方程或绕射理论进行波浪荷载计算［1-3］。然而，对于不规则波，不同波浪成分对应的波长不同，如图7 所示，因此通过谱峰周期选取计算方法进而对波浪力进行计算难免会影响其他波浪组分的计算结果。

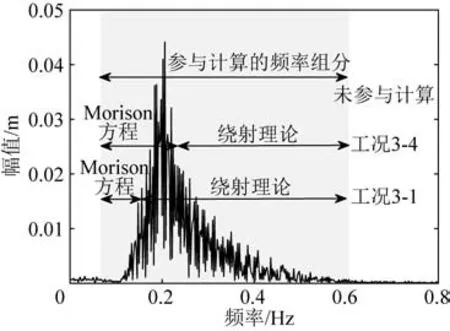
图7 不同工况波浪频率分布Fig.7 The wave frequency distribution in different working conditions

如图8 所示，给出不同圆柱直径、谱峰周期和有效波高工况下，Morison 方程和绕射理论在不同尺度因子下的拟合优度。由图8 可知：随着D/L的增大，Morison 方程的拟合优度呈指数下降的趋势，当D/L＞0.2 时，Morison 方程的拟合优度在0.85 以下；绕射理论的拟合优度所有工况均在0.9以上，说明其在这里选取的工况下计算单桩基础的波浪力适用性较好。此外，绕射理论大体上随着D/L的增大呈现先增大后减小的趋势。

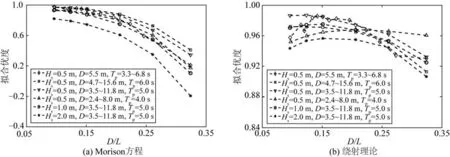
图8 Morison方程和绕射理论在不同尺度因子下的拟合优度Fig.8 R2 of Morison equation and diffraction theory at different scale factors

值得注意的是，即使有相同的尺度因子，不同的谱峰周期和有效波高工况下，两种方法和数值模拟的拟合优度仍有所差别。对比工况3-1～3-6、4-1～4-6、5-1～5-6可知：Morison方程的精度随着有效波高的增大而减小［18］，即使D/L在0.2以内，在波高小于1.0 m 时拟合优度尚在0.75以上，当波高为2.0 m 时拟合优度仅余0.6；反观绕射理论，其精度虽然随着波高的增加略有下降但其拟合优度依旧保持较高水平。对比工况2-1～2-3、3-1～3-6、6-1～6-6可以发现两种波浪力计算方法对周期均不敏感。

由此可知：在计算单桩基础的不规则波波浪力的过程中，小波高工况下（HS= 0.5 m），Morison 方程在D/L＜0.2 时尚且适用；当波高较大时（HS= 2.0 m）时，Morison 方程在D/L＜0.12 时才能具有较高的精度。同时，虽然规范中绕射理论仅适用于大尺度因子的波浪力计算，但是经过研究发现，在实际海上风电单桩基础的尺度范围内，采用绕射理论计算波浪力是完全可行的，且其精度普遍高于Morison 方程，因此后续波浪力的计算均建立在绕射理论基础之上。

图9 给出了2 个代表性工况的波浪荷载时程曲线，其中图9（a）为工况3-4，图9（b）为工况3-1。工况3-4中Morison 方程和绕射理论的计算结果与数值模拟结果在时域上均较为吻合，其中Morison 方程结果相较绕射理论偏差稍大。在该工况下虽然依据谱峰周期计算的尺度因子D/L= 0.151，规范上推荐使用Morison 方程进行计算，但是绕射理论在该尺度下的计算精度依旧更高。从图9（b）中可以看到：在工况3-1下绕射理论结果依旧良好，Morison 方程计算结果在该尺度下虽然在相位上符合但是在幅值上已经明显偏大，说明在尺度因子较大的工况下Morison方程已经适用性较差。

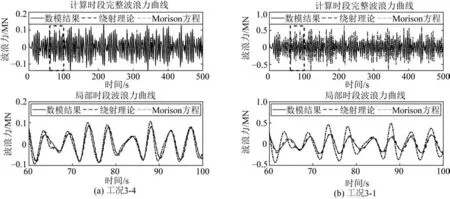
图9 数值模拟波浪力和重构波浪力对比Fig.9 The comparison of numerical simulation and reconstructed wave force

为了进一步探究Morison 方程计算结果偏大的原因，对三者计算结果进行频谱分析，如图10 所示，结果表明：在低频段（图10（a）中小于0.25 Hz，图10（b）中小于0.15 Hz）三者的波浪力频谱幅值基本一致，而在高频段Morison 方程的幅值明显高于数值模拟和绕射理论结果。由此可以看出Morison 方程在D/L较大时不准确是由高频波浪分量引起的。此外，对比图10（a）和10（b）可以发现Morison 方程的幅值在高频成分的误差随着D/L的增大而增大。

图10 不同理论的波浪力频谱对比Fig.10 The spectrum comparison of wave force with different theories

图11 对应工况3-4 的单个谱峰周期内的波面云图，从图中可以看到：由于圆柱尺度较大，圆柱的近场波浪已经受到了明显的扰动，圆周径向产生绕射波浪场，近场波浪波峰抬升，波谷降低。相应的，此时仅采用无修正的Morison方程或者仅计算未扰动波浪场下的F-K力是不合适的，该扰动场波浪力的计算应当考虑绕射作用。

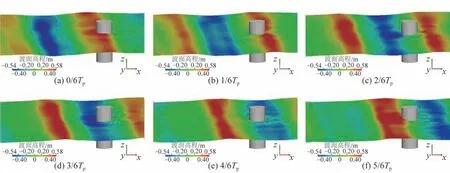
图11 工况3-4单个谱峰周期内波面云图Fig.11 Wave cloud plot within a single spectral peak period in the working condition 3-4

4 实测数据分析

4.1 实测波面获取

在2021 年5月至2022 年2月为期10个月内，江苏如东鲁能H14-37#风机近场海域波浪数据采用波浪监测雷达进行采集。雷达位于风机套笼外平台与海面悬空处，距离泥面19 m，平台与海面之间无遮挡物，波浪雷达可直接照射到水面，远程监测水位、波向、波高、波周期和潮汐，波高观测范围0～60 m，测量频率最高可达10 Hz，如图12所示。

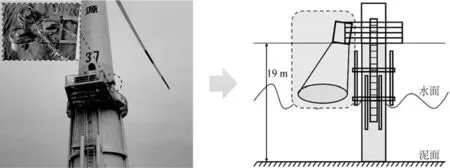
图12 雷达布置示意Fig.12 Schematic diagram of the radar arrangement

4.2 实测波面分析

选取监测时间段内如表4所示的代表工况进行分析，以10 min为一数据段求解有效波高与有效周期，得到如图13所示的统计结果，有效波高涵盖了0.2～2.5 m，有效周期涵盖了3～10 s。监测海域以风浪为主，波浪的波高与周期基本成正相关，较大的有效波高通常对应着较大的有效周期；波浪的波高与周期随着潮汐作用变化明显，波高与周期均随着潮位的增高而增大。对全天的波高数据进行快速傅里叶变换得到如图13（d）所示频域分析结果，波浪能量主要分布在0.1～0.2 Hz，整体谱型与标准JONSWAP谱差别较大。

表4 实测工况选择Tab.4 The selection of actual test conditions

图13 实测波高数据分析Fig.13 The analysis of measured wave data

2021年7月25日为台风过境，该日波高极大值为2.60 m，周期极大值达10.00 s，此外，观察图13（c）可知当日为天文大潮，水深变化显著大于其他工况，更能代表恶劣海况；2021年8月1日代表一般平静海况，其全天有效波高为0.43 m，全天有效周期为4.82 s，该工况为前文数值模拟的标准工况；2021年9月30日为风浪、涌浪联合作用的代表工况，由图13（b）可知该日后半日波浪周期显著增大，由图13（d）可知该日波浪频谱出现明显的双峰，其中主频分别约为0.06 和0.20 Hz，其中0.06 Hz 的波浪成分为涌浪，0.20 Hz 的波浪成分为风浪；2021年10月15日波高逐渐增大，其波高的变化脱离潮汐变化规律。

4.3 基于实测波面的波浪力分析

通过实测波面数据进行波浪力重构以判断不同工况下的波浪力特征，参与计算的波浪成分由图13（d）选取0.01～0.80 Hz。图14（a）为各工况60 s内波浪力计算时程，其中：台风工况下波浪力幅值达到400 kN，平静工况下约为100 kN，台风时桩基所受波浪力为平静工况下的4 倍以上；在波高变化工况，波浪力时程也随时间有明显增大。图14（b）为对波浪力的频域分析，其谱型结果与波高频谱相当，主要频率位于0.1～0.2 Hz，且更高的波浪幅值对应着更高的波浪力幅值；此外，相较于波浪频谱，混合浪工况下虽然波浪力低频成分幅值占比变小，但是仍能观察到明显的双峰谱现象，因此，虽然混合浪工况和平静工况下的波浪力频谱主峰接近，均为0.23 Hz，但是从时程曲线来看，混合浪工况的部分波浪力周期大于平静工况。

图14 波浪力分析Fig.14 The analysis of wave forces

基于10 min 波面数据段应用绕射理论求解波浪力，以此得到波浪力和波浪要素之间的关系，为方便表示，此处波浪力选取有效波浪力（最大三分之一波浪力的均值）。如图15（a）所示，虽然不同的工况结果略有差异，如在相同有效波高下，2021 年10 月15 日的有效波浪力略大于7 月25 日的结果，但是波浪力总体上依旧正比于波高，可以认为有效波浪力随着有效波高的增大线性增大。如图15（b）所示：有效波浪力周期与波浪周期整体一致，但是两者的一致性低于有效波高与有效波浪力幅值的关系；并且随着波浪周期增大，有效波浪力周期与波浪周期之间的偏差呈增大趋势。

图15 波浪力影响因素分析Fig.15 The analysis of influencing factors of wave forces

5 结 语

基于Morison 方程与绕射理论通过波面求解了不规则波面对海上风电单桩基础的波浪荷载，以数值模拟结果为基准定量描述了不同尺度因子下两种波浪力计算方法的准确性，与此同时探究了影响计算精度的主要因素，确定了波浪力计算过程中采用的计算方法。最后，基于实测波面数据计算了单桩基础所受波浪力，分析了实际海域中波浪力特征。主要研究结论如下：

1）在海上风机桩基础的尺度范围内：Morison 方程计算的水平波浪力整体上大于数值模拟结果，在频域表现为低频组分波浪力较为准确，高频组分波浪力幅值偏大；绕射理论与数值模拟结果吻合良好。

2）Morison 方程计算结果和数值模拟结果的拟合优度随着D/L的增大呈指数减小的趋势，绕射理论的拟合优度均保持在0.9以上。

3）在尺度因子相同的条件下，Morison 方程的拟合优度随着有效波高的增加而减小。在小波高工况下（HS= 0.5 m），Morison 方程在D/L＜0.2 时尚且适用；当波高较大时（HS= 2.0 m）时，Morison 方程在D/L＜0.12时才能具有较高的精度。相较而言，在海上风机桩基础的尺度范围内，绕射理论计算精度高于Morison 方程且受波高影响较小，因此建议工程上采用绕射理论求解海上风电基础波浪荷载。

4）台风期间波浪力显著增加，最高可达平静海况波浪力的4倍以上。此外，基于实测波面计算的有效波浪力随着有效波高的增大线性增大，波浪力周期与波浪周期成正相关，但其相关性低于波浪力与波高的相关性。