多连通域浮式平台波浪载荷水池模型试验研究
2024-03-12耿彦超王琦彬凌宏杰邬志佳朱云龙谢卓雨
耿彦超,丁 军,俞 俊,王琦彬,凌宏杰,邬志佳,朱云龙,谢卓雨
(1.中国船舶科学研究中心,江苏 无锡 214082;2.深海技术科学太湖实验室,江苏 无锡 214082;3.江苏科技大学,江苏 镇江 212003)
中国海洋国土面积约300万平方公里,海洋超大型浮体具有广阔的应用前景[1]。一般而言,海洋超大型浮体是由若干个基本模块按功能需求拼装组成,具有可迁移、组装、重构及适应恶劣海洋环境的能力,是可在中国的大型船坞中制造,并被拖带到选定的礁滩附近系泊定位的浮式结构组合体。不同规模的海洋超大型浮体装载不同的设备系统,可为海洋油气资源勘探开发、海洋生物考察研究、海洋环境调查管理、海洋渔业生产储运、区域海空安全监控、旅游服务等提供综合保障[2]。多连通域复杂构型浮式平台的典型代表是大型海上旅游浮式综合体,多连通域复杂构型浮式平台内部存在连通水域,同时引起通道内水体流动和交换。在波浪激励下这种类似于半封闭港湾的内域水体很可能发生港湾共振现象,因此需进一步研究并掌握其内域水体谐振特性。
针对多连通域复杂构型浮式平台的水动力分析,会涉及到内外域流场相互影响、内域限制水域水体共振、局部波浪砰击和甲板上浪等关键问题,传统的理论方法无法进行有效评估,且相关新理论方法在国内外还未见报道,严重制约了该类浮体的研发及工程化应用进程[3]。此外,大型多连通域浮体具有水平尺度大、垂向尺度小且内部水域尺度大的特点,其结构刚度较小,故分析其在波浪作用下的响应时必须考虑水弹性效应。因此针对多连通域复杂构型浮体内外域自由面不连续但水下有水体交换的特点,有必要进一步开展多连通域浮体水弹性响应分析,并掌握内域水体流动对多连通域浮体整体运动响应的影响规律[4]。
由于多连通域浮体概念仍是一个比较新颖的设计理念,国内外直接针对多连通域浮体的水动力分析理论方法尚未见报道,国内外针对多连通域浮体构型特征及流域特征,将其水动力分析的核心问题集中在浮体内外流域耦合效应和限制水域水体共振及抑制措施等方面。
多连通域浮体由于其特殊的构型,其将整体流域分为多个连通或不连通的流域,各流域在交界面处存在流体交换,同时,各个流域与浮体之间存在相互影响,为此,需要重点考虑内外流域的耦合效应。针对底部连通式多连通域浮体,国内外学者基于势流理论,采用半解析法、模态函数展开法,并针对特有问题,采用区域分解方案,考虑上下流域交界处应用速度势匹配条件,解决了底部连通浮体内外流域耦合效应[5-9];对于侧向连通式多连通域浮体,类似侧向破损船舶,一般利用势流理论、CFD 或者两者相结合的方法,比如部分研究工作采用势流方法处理船舶运动,而采用黏流方法处理破损流动,充分结合了两类方法的特点,在精确模拟破舱进出水即内部流动的情况下,减少了计算时间[10-11];当大型多连通域浮体内部流体运动频率与流体系统固有频率接近时,流体将出现剧烈运动的情形,表现出共振特征,其引起的砰击与上浪等现象对于浮式结构物的安全造成巨大的隐患,必须在浮式结构物的设计、建造和运行等全寿命周期内重点关注该现象,针对这一内域共振问题,Wang 等[12]考虑流体黏性,利用时域数值水池,研究了多桩柱在规则波作用下的水体共振问题,结果表明流体黏性对结构物内部水域的波面幅值具有明显的阻尼效应。也有学者基于势流理论,利用比例边界有限元法研究波浪与带窄缝多浮体的相互作用,结果表明,浮体吃水、浮体宽度和窄缝宽度的增大都将使得水体共振频率减小[13-14]。
在科学研究与工程实际问题中,数值方法可以作为强有力的求解手段,但是物理试验仍然是验证其计算结果合理性的主要途径。针对多连通域浮体在波浪中的载荷响应复杂、数值计算难以模拟等新问题,有必要有针对性地开展多连通域理想浮体平台的波浪载荷水池模型试验,分析测量数据,获得平台在波浪中的响应规律,水池模型试验对不同海况下4种典型多连通域浮式平台方案进行载荷测量,包括剖面的垂向弯矩、水平弯矩、扭矩等,可深入研究不同方案多连通域平台的水动力载荷特性,也可验证数值方法的正确性,为多连通域浮体设计和相关理论发展提供依据。
1 多连通域波浪载荷水池模型试验方法
1.1 多连通域方案构型
针对大型多连通域浮式平台主要构型特征,设计4 种理想构型(如图1 所示)开展波浪中平台响应试验研究。4种基本构型的主体外形均为圆形,主要区别在于内部多连通域的构成。方案一为完整圆饼型;方案二为内部存在四分之一水域的三角型;方案三为内部存在大面积水域的D 型;方案四为组合型,是在方案三的基础上增加一个横向隔撑,从而将内部水域分成半圆和梯形两部分。平台基本参数见表1。x轴沿平台中线指向艏部,y轴指向左舷,z轴垂直向上,xy平面与平台底部重合,yz平面位于中横剖面处。浪向定义:0°为随浪,180°为顶浪。文中若无特殊说明,均使用此坐标系统。4个大型多连通域浮式平台试验模型的主要参数见表2,重心位置、惯性半径等参数通过调节压铁位置来满足要求。

图1 平台构型方案示意及坐标系定义Fig.1 Schematic representation of platform configuration scheme and definition of coordinate system

表1 大型多连通域平台基本参数Tab.1 Basic parameters of large multi-connected floating platform 单位:m
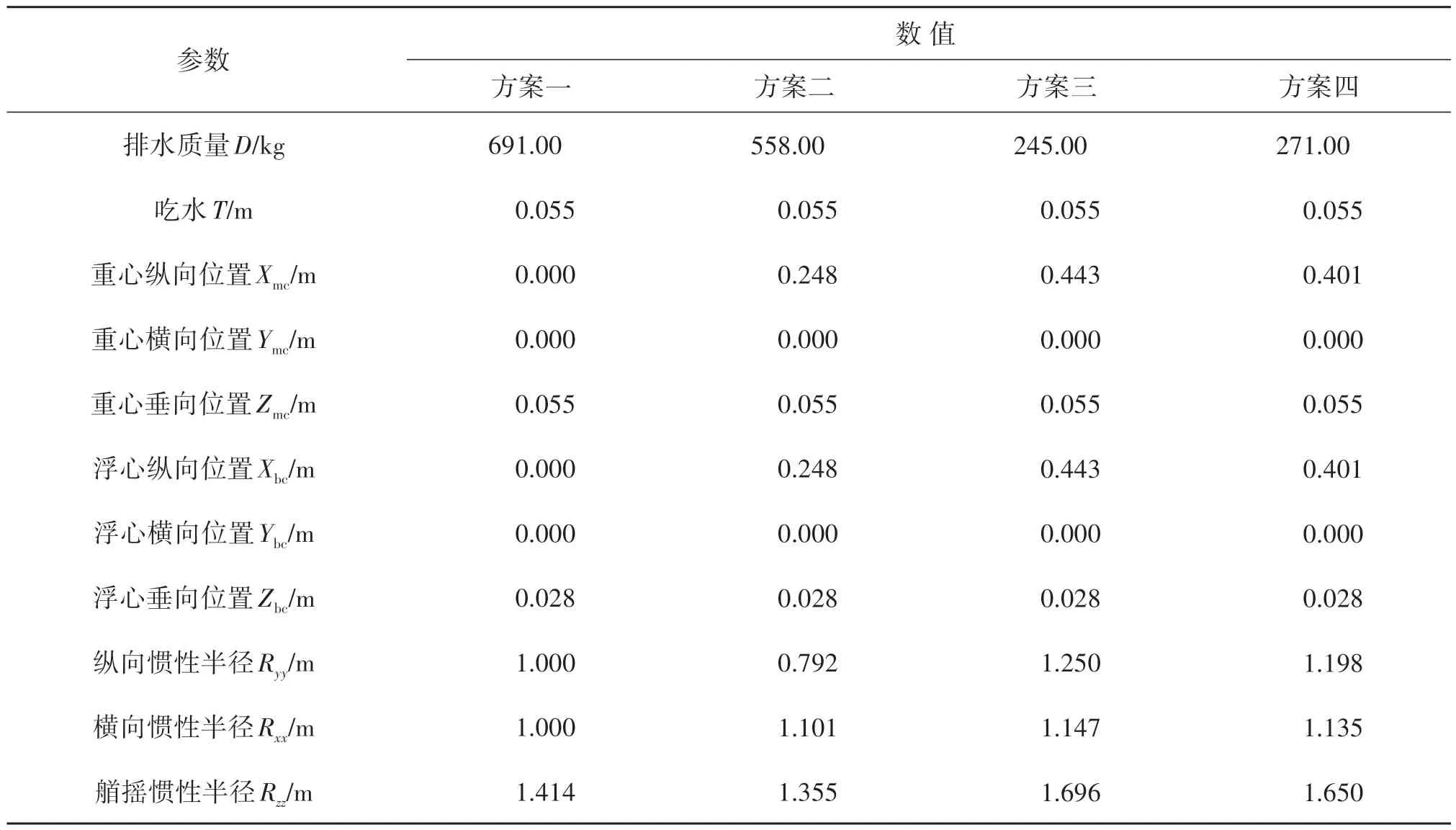
表2 大型多连通域平台物理参数Tab.2 Physical parameters of large multi-connected floating platform
1.2 多连通域水池模型试验相似关系
从多连通域原型平台机理性试验目的出发,试验缩尺模型与原型之间满足部分几何相似、运动相似、动力相似和刚度相似[15]。
几何相似要求模型和实体对应的线尺度之比为常数,可表示为:
式中:λ为模型缩尺比;Ls为实体的任一特征尺度;Lm为模型对应的线尺度。
平台在海浪中的运动是一种不定常运动,此外,平台在海浪上的运动和受力带有周期变化的性质,欲使模型与实体之间保持运动相似,必须满足斯特劳哈尔数相等,可表示为:
式中:Vm为模型速度;Vs为实体速度;tm为模型时间(包括运动周期);ts为实体时间(包括运动周期)。
动力相似主要包括惯性力和重力相似,即模型与实体满足弗劳德数相等,表示为:
多连通域实际浮体与模型关于刚度的相似准则:
式中:Es为实船材料弹性模数;Is为实船剖面惯性矩;Em为模型材料弹性模数;Im为模型剖面惯性矩;g为重力加速度。
实际模型设计时,浮体参与总纵弯曲构件沿船长的各横剖面惯性矩与材料弹性模数的乘积EI(x),按缩尺的5次方缩小,以保证弯曲振动的频率及振动形式的相似,采用圆型截面钢质梁。
1.3 模型试验介绍
为了防止多连通域平台模型在试验过程中发生过大的漂移,在平台模型四周均布4根弹簧约束系统,弹簧间成90°夹角(见图2)以水平方式连接到模型预埋的U 型接口,每根弹簧长2 m,刚度为32.5 N/m。选取弹簧刚度时,应保证弹簧系统约束引起的平台飘荡周期是平台模型六自由度固有最大周期的5 倍以上。剖面载荷响应测试主要是对图3所示的3个位置处横剖面上的垂向弯矩MV、水平弯矩MH和扭矩T进行测量。表3给出了3处剖面载荷的测量具体位置及编号信息。
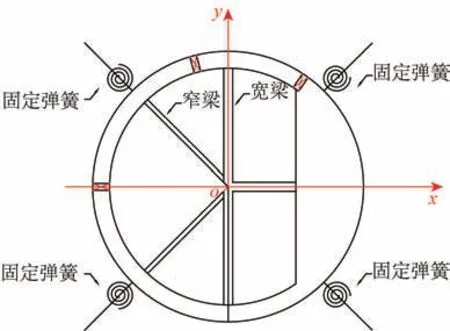
图2 弹簧固定系统示意Fig.2 Schematic diagram of the spring fixing system
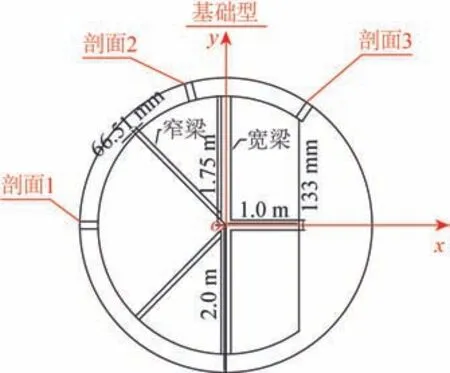
图3 测量剖面位置Fig.3 Schematic diagram of test section

表3 剖面载荷测量位置(缩尺比为1∶100)Tab.3 Positioning of section load measurement (Scale ratio is 1∶100 ) 单位: m
图4~5给出了测量梁系统与平台的连接方式,可以看出在测量剖面载荷位置平台被断开,因此该剖面的受载都由测量梁系统承担。
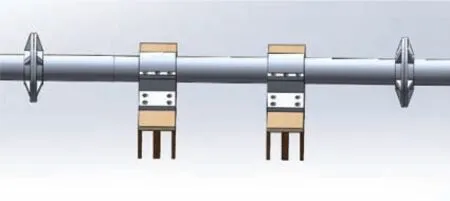
图4 测量梁系统示意Fig.4 Schematic diagram of the measuring beam system
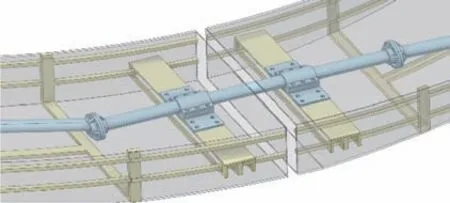
图5 测量梁系统与平台连接示意Fig.5 Schematic diagram of connection between the measuring beam system and platform
根据上述方案,加工出的平台试验模型如图6 所示。方案一波浪载荷响应较小,仅用于测量平台运动响应。

图6 多方案多连通域平台水池试验模型Fig.6 A experimental model of multi LMCFP schemes
试验采用动态应变仪进行波浪载荷的实时测量,分段处的测量梁上应变片布置如图7 所示,其中应变片G1~G2 沿梁轴纵向粘贴于梁表面,应变片G3~G6 沿梁轴纵向45°方向粘贴于梁表面。应变片G1 和G2 半桥连接通过标定形成测量剖面垂向弯矩MV(相同原理可得水平弯矩MH),应变片G3~G6 全桥连接通过标定测量扭矩T。
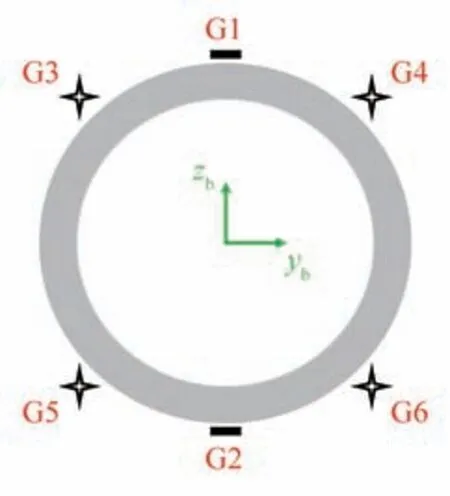
图7 剖面载荷应变片粘贴示意Fig.7 Schematic diagram of the strain gauge pasting
2 波浪载荷试验结果分析
试验开始前,选用质量远小于模型质量的锤子(约2 kg),用锤子击打平台模型刚性部位以保证模型不被损坏,锤击力的大小能促使模型在水中自由振动,记录分析平台模型在水池中的自由振动衰减曲线。以方案三为例,模型在水中自由振动时,实时记录其垂向弯矩MV3的衰减曲线,如图8所示,可以得到阻尼比为6.9%,是一般船舶的4~5倍。
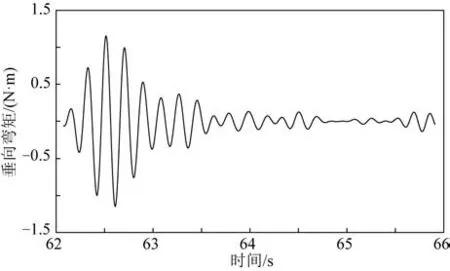
图8 方案三垂向弯矩 MV3自由振动衰减曲线Fig.8 MV3 free vibration attenuation curve
2.1 参数影响分析
在规则波试验工况下,模型试验波高为3 cm,分别给出了0°、45°、90°、135°、180°等多个浪向的试验结果。图9 为方案四180°浪向下MV3波浪矩与合成矩的对比,发现方案四在自由状态下,平台垂向载荷响应的波浪成份与合成成份差别不大,只在极少量工况下有少量高频成份产生,可以判断,平台并未发生高频振动响应。图10 为方案四自由状态下垂向弯矩MV2在不同浪向下的对比,可知垂向弯矩MV2在顶浪和随浪时较大,斜浪时较小。
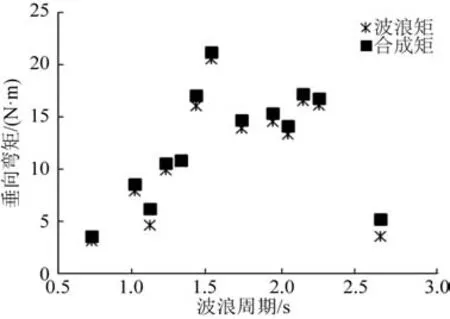
图9 方案四180°浪向MV3波浪矩与合成矩对比Fig.9 Scheme IV comparison for WM and CM of vertical bending moment MV3 in 180° waves
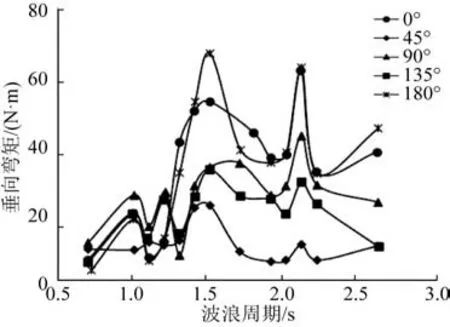
图10 方案四自由状态垂向弯矩MV2不同浪向对比Fig.10 The scheme IV comparison of different wave directions of free state vertical bending moment MV2

图11 45°浪向下不同方案垂向弯矩MV2对比Fig.11 Comparison of vertical bending moment MV2 of different schemes in 45° waves

图12 45°浪向下不同方案扭矩T3对比Fig.12 Torque T3 comparison of different schemes in 45° waves
总体来看,方案四具有典型性,波浪载荷响应最大,试验工况充分,且该方案是后续平台持续优化和将来建造的基础,因此,将该方案作为波浪载荷分析的重点。图13~16 分别给出了方案四在0°、45°、180°浪向角下垂向弯矩、水平弯矩、扭矩在两种边界条件下的对比,可以发现:垂向弯矩、水平弯矩、扭矩在自由状态和约束状态下变化趋势一致,约束状态值略大于自由状态,说明在约束状态下,多连通域浮式平台由于约束的存在,发生了部分高频振动响应。

图13 0°浪向下两种状态垂向弯矩MV1对比Fig.13 Comparison of vertical bending moment MV1 under two states in 0° waves

图14 45°浪向下两种状态水平弯矩MH1对比Fig.14 Comparison of horizontal bending moment MH1 under two states in 45° waves
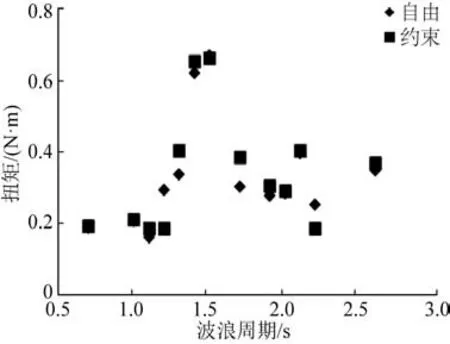
图15 45°浪向下两种状态扭矩T3对比Fig.15 Comparison of torque T3 under two states in 45°waves
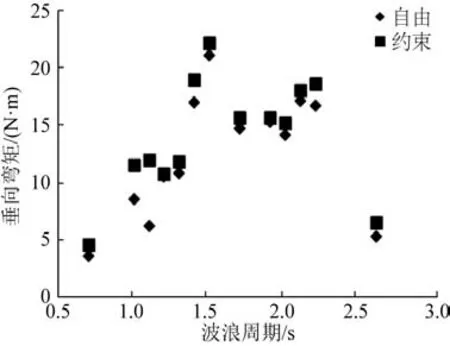
图16 180°浪向下两种状态垂向弯矩MV3对比Fig.16 Comparison of vertical bending moment MV3 under two states in 180° waves
2.2 非线性成份分析
对于方案四多连通域试验,分为自由状态和只释放垂荡状态,选取随浪0°和顶浪180°两种浪向,试验波高为5 cm,分别给出多连通域分别在自由状态和只释放垂荡状态下3 个剖面垂向弯矩的测量结果,见表4,垂向弯矩分别给出波浪矩和合成矩,并对波浪矩占合成矩的比例进行分析对比,可以发现,自由状态下的波浪矩占比都大于只释放垂荡状态,说明只释放垂荡时,平台更容易发生高频响应,但总体来看,高频成份占比都不高,说明平台不易发生明显的水弹性响应。这是由于多连通域质量大、阻尼大,高频振动并不能轻易被激起。
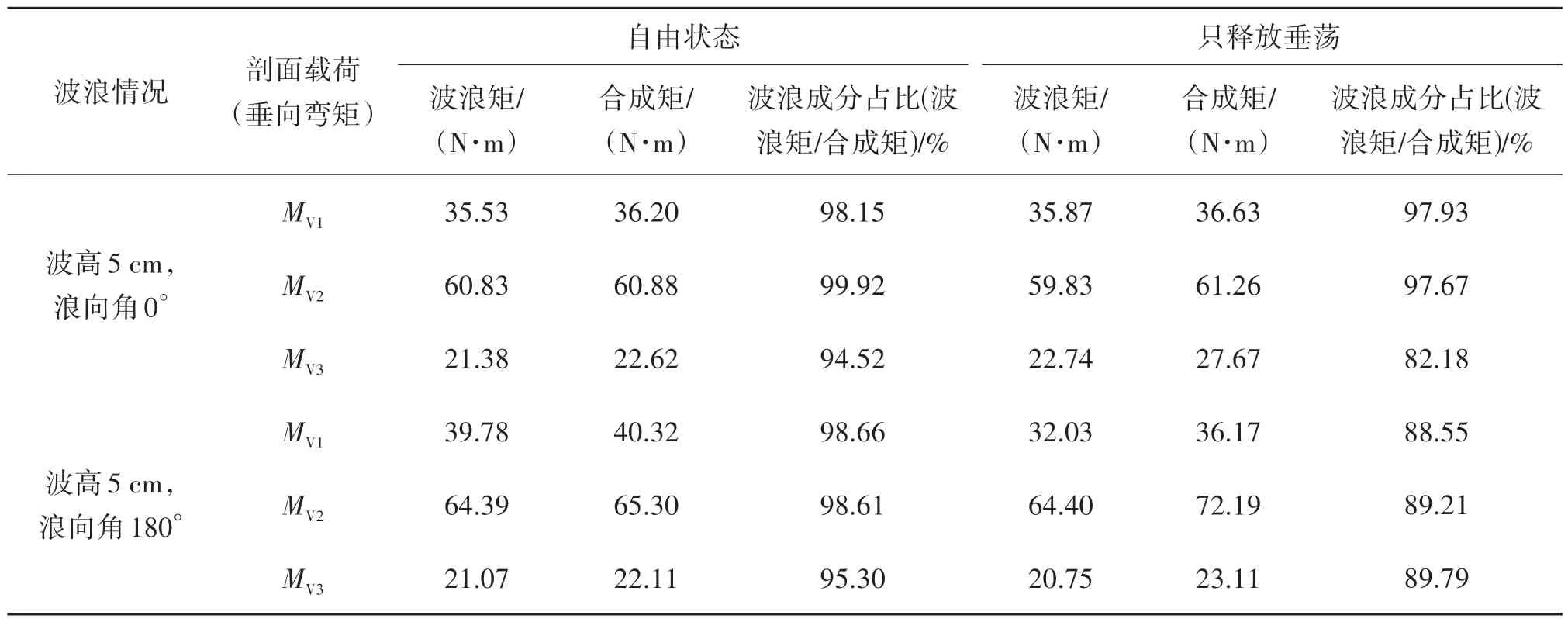
表4 方案四自由状态和只释放垂荡状态对比Tab.4 Scheme IV comparison between the free state and heave only state
图17~18 给出方案四自由状态、0°浪向角、试验波高5 cm、周期2 s 时(工况代号为A8-15)的弯矩时域曲线、频谱图。此时,平台是一个整体的弹性体,从时域及频谱图来看,平台除了低频的波浪响应外,并无明显的高频响应。

图17 A8-15工况MV3弯矩时域曲线Fig.17 The time domain curve of MV3 bending moment under A8-15 condition
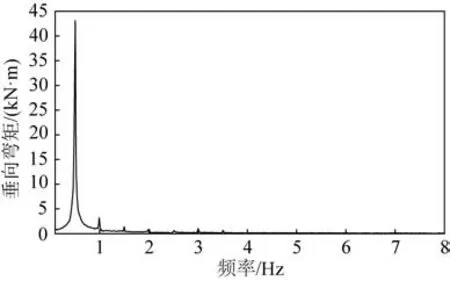
图18 A8-15工况MV3弯矩频谱成份分析Fig.18 The frequency spectrum analysis of MV3 bending moment under A8-15 condition
图19~20 给出了水弹性响应相对比较明显的方案四在约束状态、0°浪向角、试验波高5 cm、周期2 s 时(工况代号为B1-15)工况的弯矩时域曲线、频谱图。在这种条件下,多连通域平台除了受到波浪的外力作用外,还有约束柱与平台之间耦合响应力的存在。从时域曲线看,发现有高频成份叠加在低频的波浪弯矩上;从频谱图来看,存在多个频率成份,这些高频率成份包含了波浪的非线性、约束柱与平台之间的耦合、平台的高频振动(水弹性响应)等。

图19 B1-15工况MV3弯矩时域曲线Fig.19 The time domain curve of MV3 bending moment under B1-15 condition
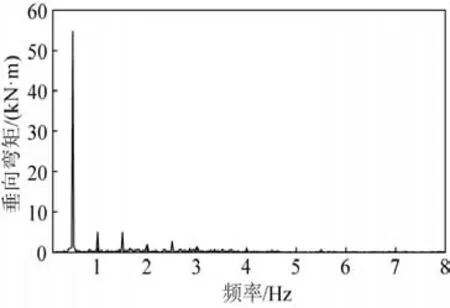
图20 B1-15工况MV3弯矩频谱成份分析Fig.20 The frequency spectrum analysis of MV3 bending moment under B1-15 condition
3 结 语
基于开展的多连通域平台波浪载荷水池模型试验,通过数据处理分析,给出了多连通域浮式平台的波浪载荷响应特征,分析了规则波下载荷的响应特点,总结出以下几条结论:
1)总体来看,平台高频成份占合成矩比例都不高,说明平台不易发生明显的水弹性响应。这是由于多连通域质量大、阻尼大,高频振动并不能轻易被激起。
2)多连通域浮式平台在自由状态下载荷值基本都小于平台只释放垂荡状态载荷值。
3)在方案四高波高状态下,多连通域平台除了受波浪的外力作用外,还有约束柱与平台之间耦合响应力的存在,时域上高频成份叠加在低频波浪弯矩上,频域上存在多个频率成份,这些高频成份包含了波浪的非线性、约束柱与平台之间的耦合、平台的高频振动等。
