SEIAR模型在应急医疗物资动态分配优化中的应用

梁 迪, 辛 江, 李羽婷, 卢列兆

(沈阳大学 机械工程学院, 辽宁 沈阳 110044)

近些年,世界多地受到突发性公共卫生事件侵扰,例如,2009年的甲型H1N1流感,2014年的西非埃博拉疫情,2019年底开始蔓延全球的新冠肺炎疫情等,不仅对农业、工业产生了严重影响,而且造成了严重的生命损失,导致持续的经济低迷[1]。突发公共卫生事件对人们健康的危害以及社会经济等影响十分严重。因此,在疫情防控过程中,了解需求地所需的物资量以及如何使物资既满足受灾地区需求又经济快速地分配,成为世界各国政府部门以及专家学者重点关注的问题。

学者们大多采用各种预测模型来判断疫情走势,然后构建相关物资分配模型并采用智能算法对模型进行求解,本文学习以往学者的研究方法,并认真选择相关文献进行深入研究。

1) 研究了预测模型。在现有的突发疫情传播规律研究成果当中,学者们大多使用时间序列模型以及各类传染病模型(SI、SIS、SIR、SEIR[2-3]等)。Pathan等[4]通过实例证明时间序列模型可以准确预测COVID-19病毒每日基因突变率。李冯等[5]将无症状感染者引入传统的SEIR模型当中,有效增强了新模型的拟合精度。Chen等[6]提出了一种改进的SEIUR模型,对美国新冠疫情数据进行数值模拟。Meiksin等[7]利用带有附加污染物的动态SEIR模型,分析了一种在统计上量化污染物对病毒流行病传播的贡献方法。

以上学者主要研究了在公共卫生事件中预测模型的应用情况,通过模型可以更好地预测疫情未来的走势,然后根据不同卫生事件的特点对模型进行改进,进而使得预测的结果更贴合实际。

2) 研究了应急医疗物资分配的问题。Lei等[8]和王小纯等[9]为解决地震中人员分配和物资供应问题,构建了以总延误时间最小为目标的两阶段供应链网络模型。Büyüktahtakin等[10]为减少西非埃博拉病毒对人类造成的危害,根据空间位置的动态性为目标构建了整数规划数学模型。李珍萍等[11]为减少应急医疗物资分配过程中的损失,建立以存储成本和期望损失和最小为目标的两阶段随机规划模型。

以上学者主要研究了在公共卫生事件中如何对人员以及医疗物资进行分配的问题,为最大限度地减少生命财产损失,学者们通常考虑如何将应急医疗物资或者医护人员以最短的时间送到需求地,有效解决需求地的生命财产损失,并防止疫情的进一步蔓延。为此,构建了以配送时间最小化、满足率最大化等为目标的分配模型。

3) 研究了多目标优化算法。李荣雨等[12]、智洪欣等[13]将莱维飞行策略引入粒子群算法中,仿真结果显示优化后的算法有不易发生早熟、后期收敛速度快、不易陷入局部最优等特点。Kundu等[14]提出了一种用于高维微阵列数据特征选择的利他鲸鱼优化算法,基于元启发式的特征选择可以有效地从大量属性中筛选出相关基因。本课题组前期[15-16]为改进算法的高效性,分别将余弦递减策略融入鲸鱼算法以及以支持向量机和布谷鸟搜索算法结合的方式对算法进行优化。

随着学者们的不断深入研究,越来越多的启发式算法被应用在物资分配、特征提取和预测等问题中。学者们通常针对在算法运算过程中易陷入局部最优、全局搜索过程慢等问题对算法进行相应改进,然后通过函数或者算例进行验证,同时与改进之前的算法或者其他算法进行对比,以此评估所提算法的优缺点。

以上研究见证了在疫情走势预测、物资分配及优化算法当中主要使用的研究方法,然而,针对新冠肺炎疫情,少有学者通过无症状感染者以及人员流动变化两个相关特点对传染病模型进行改进。而且学者们多以物资满足率最大化、运输时间最小化、总成本最小化中的一个或两个目标构建物资分配模型,将三者同时考虑并将目标赋予权重在物资分配的研究相对较少。在求解模型方面,少有学者同时考虑鲸鱼优化算法易陷局部最优、全局搜索慢这两方面的问题对算法进行改进。

1 构建应急医疗物资分配模型

为简化模型求解过程,给出如下假设:

① 无症状感染者以及感染者都具备传染性;

② 紧急医疗供应商是已知的,在每一阶段开始时确定现有医疗供应商的数量和类型;

③ 忽略天气、道路堵塞等因素影响;

④ 需求地感染人数与物资需求成正比,感染人数可以进行预测;

⑤ 迁移率按照某一周期内的平均值计算。

1.1 构建SEIAR预测模型

图1为SEIAR模型的5大类:S(易感染者)、E(暴露者)、I(患病者)、A(无症状感染者)、R(康复者)。

图1 SEIAR传染病模型示意图

引入迁移率的SEIAR模型可用式(1)～式(5)表示:

式中:Sj(t)、Ej(t)、Ij(t)、Aj(t)、Rj(t)分别表示需求地j在t时间段的易感染者、暴露者、患病者、无症状感染者、康复者;λj表示疫区j的传播率;N为人口数;Nj表示疫区j的总人数;σj表示疫区j的感染率;αj表示疫区j的患病者感染率;βj表示疫区j的无症状发生率;γj表示疫区j的康复率;dj表示疫区j的自然死亡率;bjk表示j中人群迁移到k的迁移率。通过该模型可以得到该地在t时间段内医疗物资的需求量,如式(6)所示:

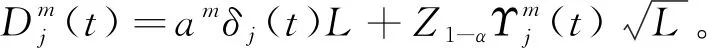
(6)

式中:am为某一需求地的某一患者在一定时间内需要的物资总量;δj(t)表示需求地j在t时间段内需要救济者数量;L表示需求物资到货时间上限;Z表示地区未感染率系数。其中,

(7)

表示为j地区在t时段内对某一物资m需求总量的标准差。

1.2 构建物资分配模型

相关符号说明如表1所示。

表1 符号说明

模型的目标函数以及约束条件如下所示:

其中:式(8)～式(10)为目标函数;式(8)为物资的满足率最大化;式(9)为车辆以最短的时间到达受灾地区;式(10)为车辆以最低的成本将物资从供应点运达受灾地;式(11)为物资的需求紧迫度计算;式(12)为物资的饱和度计算;式(13)为规定载重;式(14)为车辆对受灾地区投放的物资不能多余该地需求的上限值;式(15)为避免出现多次配送现象;式(16)和式(17)为运输车辆在某一地区完成物资投放后,直接前往下一灾区;式(18)为车辆完成配送后都在供应点集合;式(19)和式(20)为可变参数的取值约束;式(21)为物资成本不得大于收益成本。

首先,取需求地满足率最大化目标函数的倒数,将其转化为求最小值问题,将目标函数(8)转换为如式(22)所示的求最小值问题,

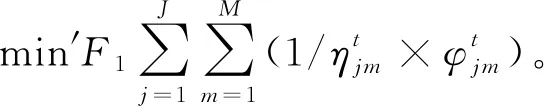
(22)

然后,用线性加权的方法把多目标问题转化为单目标问题。为消除量纲的影响,将目标函数归一化处理,并加权欧几里得距离计算目标值与理想点的距离,定义目标函数F′1的最优值与最劣值分别为F′1min、F′1max,目标函数F2的最优值与最劣值为F2min、F3max,目标函数F3的最优值与最劣值为F3min、F3max,公式如下:

式中,α,β,γ为由专家根据实际情况给出3个目标的函数的期望权重,并且α+β+γ=1。

2 算法设计

鲸鱼优化算法(whaleoptimizationalgorithm,WOA)是Mirjalili等[17]在2016年提出的一种基于座头鲸鱼狩猎方法的元启发式算法。

2.1 精英反向学习策略

为增强基础鲸鱼算法种群的多样性,将精英反向学习策略融入算法中,

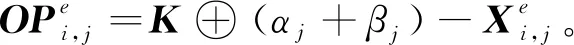
(25)

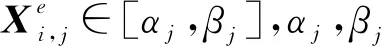
2.2 非线性自适应惯性权重

为提升鲸鱼算法在运算过程中的局部搜索能力以及在运算前期的全范围搜索能力,运用非线性的自适应惯性权重来更改公式进而使鲸鱼位置发生改变,

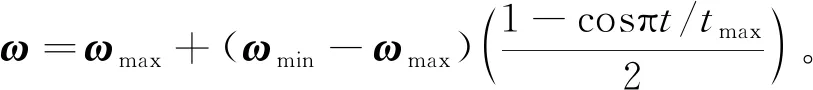
(26)

式中:ωmax为非线性自适应权重的最大值;ωmin为最小值;t表示某一时刻的迭代次数;tmax为最大迭代次数。

ω的取值随迭代次数增加呈非线性递减趋势,不仅保证了鲸鱼较强的全局搜索能力,而且有利于鲸鱼局部范围内寻优,进而提高了算法的运算性能。改进后位置更新如下:

式中:b为常量系数;l为[-1,1]之间的随机数;其中A和C为相关系数:

式中:r是[0,1]之间的随机数;a为收敛因子,其随迭代过程从2线性减少到0,

a=2-2t/tmax。

(31)

2.3 莱维飞行策略

将莱维飞行应用于鲸鱼的位置更新中,在算法进行更新后再进行一次莱维飞行更新个体位置,可以实现跳出局部最优解,扩大搜索能力的效果。位置更新的方式为

X(t+1)=X(t)+α⊕levy(λ)。

(32)

式中:α为步长缩放因子;levy(λ)为随机步长;⊕表示点对点乘法。莱维飞行概率密度函数及生成随机步长的公式如下:

即进行更新时,levy(λ)使用S表示;进行计算时,参数β取值为1.5,α取值为1,u～N(0,σ2),v～N(0,1),σ取值为

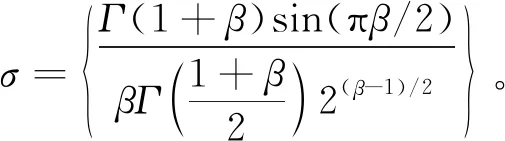
(35)

2.4 算法流程图

改进鲸鱼算法通过精英反向学习策略初始化种群,通过莱维飞行策略避免陷入局部最优,引入非线性自适应权重使算法在局部寻优时提高收敛精度,具体步骤见图2。

图2 算法流程图

3 应用案例及分析

选取2021年某地发现的新冠肺炎传染病为例,抽取当时疫情比较严重的15个地区进行算例验证,为简化计算流程,仅以各个灾区需要的防护服及防疫药品这2种医疗物资为例。从该地政府网站、市卫健委网站上下载得到SEIAR模型相关参数值,假设疫情防控中心可以提供8辆运输车,其中每辆车的行驶速度相同,各节点之间行驶距离从百度地图计算得到,人口参数(常住人口、自然死亡率、迁移率)来自该地统计局。

利用MATLAB 2018b对AWLWOA算法进行仿真模拟实验,实验硬件环境为11th Gen Intel®Core i5-35G7@2.40GHz,16GB内存,64位Windows 0操作系统。运用平均绝对误差法(MAE)和均方根误差(RMSE)验证改进的SEIAR模型准确性,并与SEIR模型和整合移动平均自回归模型(ARIMA)[18]进行对比,如表2所示,预测曲线如图3和图4所示。

表2 预测模型误差分析

图3 SEIAR与SEIR模型预测曲线对比

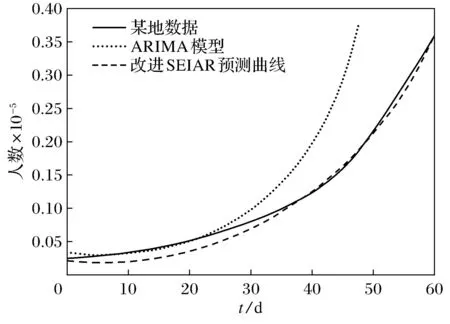
图4 SEIAR与ARIMA模型预测曲线对比

由表2可知,引入迁移率的SEIAR模型相较于未改进的SEIR模型平均误差值降低了近51%,相比于ARIMA模型平均绝对误差值降低了近35%,同时在均方根误差值方面也分别降低了近31%和22%,说明改进后的SEIAR模型在误差方面更具有优势。通过图3以及图4可知,改进后的SEIAR模型预测曲线相较于另外2种模型更贴进实际值,证明引入迁移率的模型准确性更高。

从图5可知,改进WOA算法、GA算法和PSO算法分别在39、46、53次迭代后趋于稳定,而且改进的鲸鱼算法相比另2种寻优结果更好,最优值更低。为保证本次仿真实验的有效性及所提算法的鲁棒性,对上述算法分别进行200、400和600次迭代,分别运行10次,结果如表3所示。

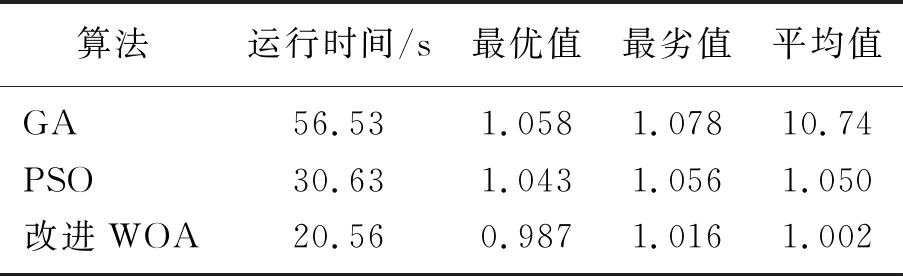
表3 三种算法实验结果对比

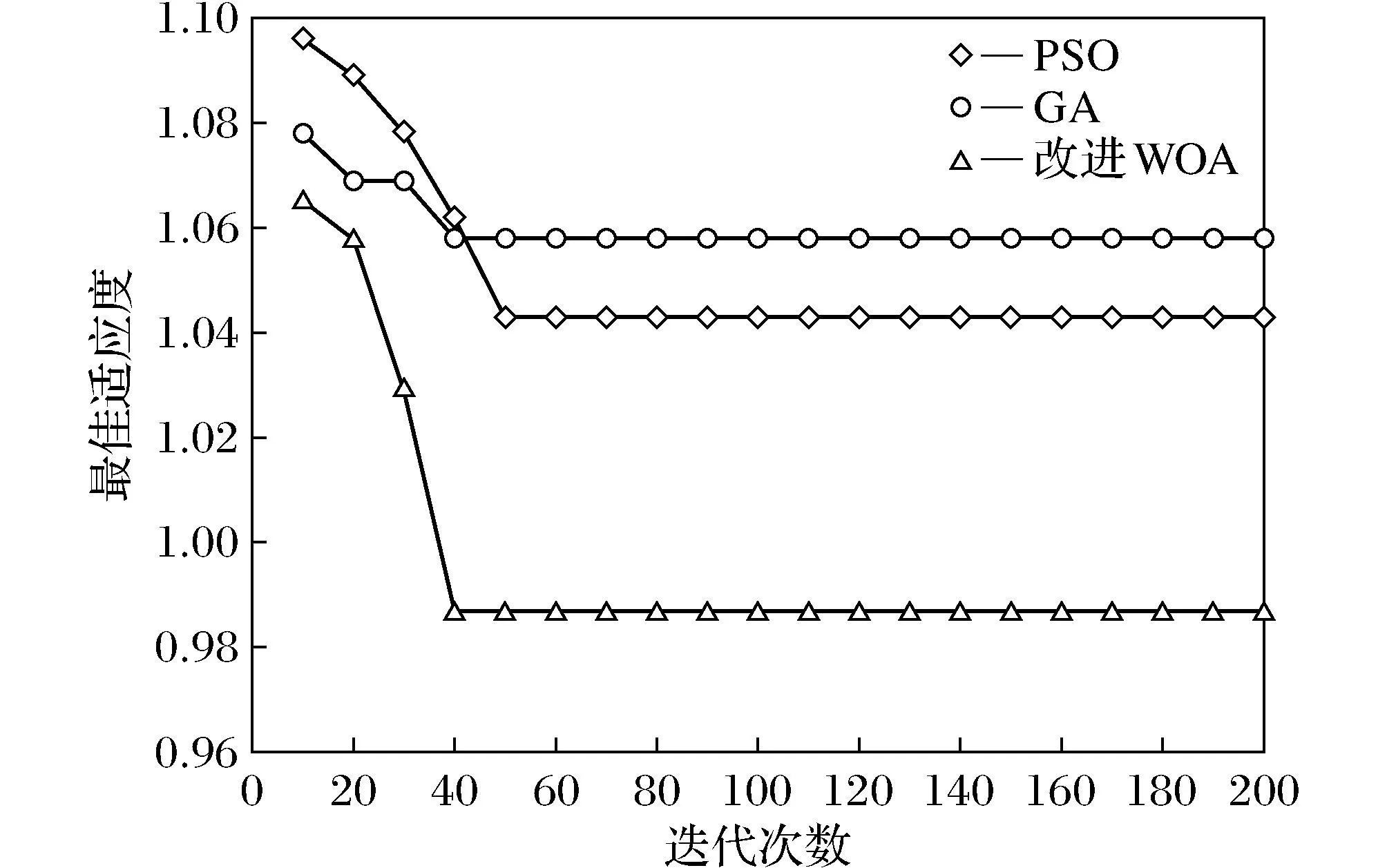
图5 三种算法求解趋势对比

从表3可以看出,改进WOA运行时间最短,为20.56 s,明显快于另外2种算法,而且最优值为0.987,相比其他2种算法求解精度更高,从3种算法的10次实验平均值来看,改进鲸鱼算法的平均值为1.002,在精准度方面依然比其他2种算法更优。

表4为下一周期的物资分配方案。

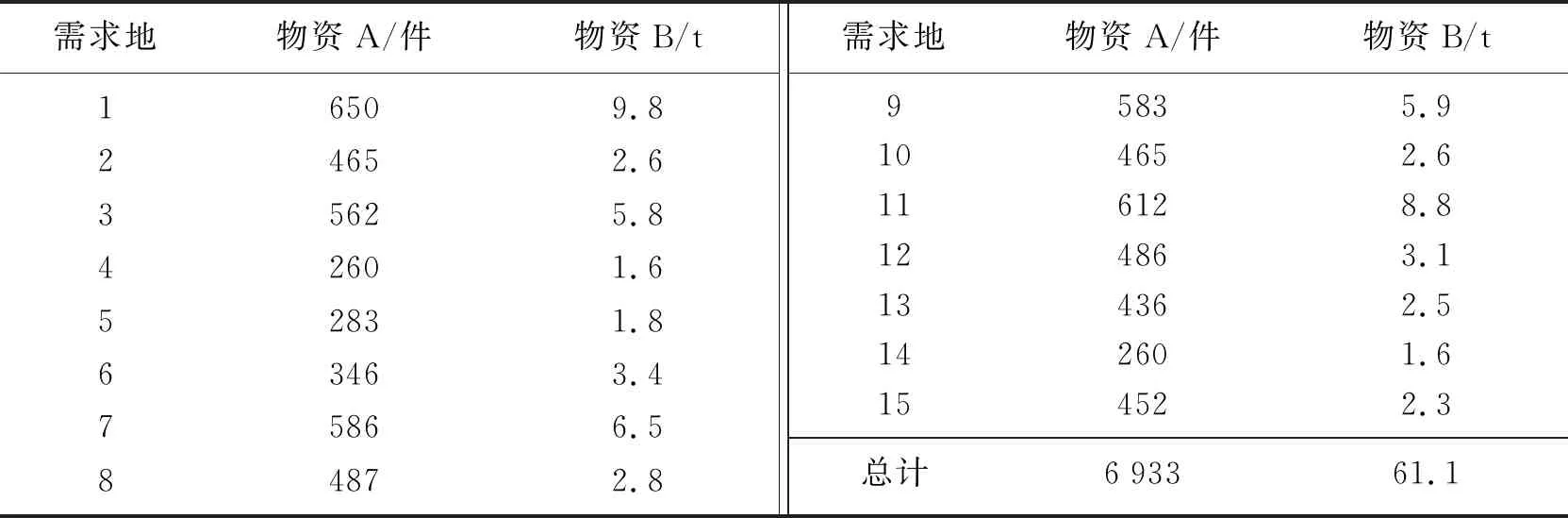
表4 物资分配方案

4 结 语

为解决突发性应急事件对受灾地区的影响,本文提出一种改进的SEIAR模型间接预测需求地医疗物资需求量,并构建多目标应急医疗物资动态分配模型对物资进行分配,最后提出一种改进的鲸鱼算法对模型进行求解。结果表明:

1) 引入无症状感染者以及迁移率的SEIAR平均绝对误差值相比未改进模型降低了51%左右,相比于ARIMA模型降低了35%左右,均方根值相比未改进模型降低了31%左右,相比于ARIMA模型降低了22%左右。

2) 结合某地实际案例验证所构模型的有效性及所提算法的可行性。通过10次算例验证的平均值表明,AWLWOA算法相比于遗传算法以及粒子群算法,运行时间最快为20.56 s,而且分别在迭代39、46、53次趋于稳定,说明算法收敛速度快,稳定性好。同时目标最优值分别提高了0.071和0.056,目标平均值分别提高了0.072和0.048。说明改进后的算法求解物资分配模型的精度更高。

改进的SEIAR模型结合物资分配模型在疫情防控中发挥积极作用,可以提前判断疫情走势,做好应急医疗物资准备工作,提高疫情防控工作效率。由于疫情扩散程度多变,政府会制定不同的防控政策,而这恰好会影响SEIAR传染病模型,而本文并未将其考虑在内。此外,本文只考虑了单一分配中心对多目的地进行物资分配,未来将考虑政府制定的防控措施以及多分配中心联合对多目的地进行物资分配问题的研究。