航天器用水热管冻结特性数值模拟研究

牟玉鹏 刘剑术 李小斌 张红娜 李凤臣 韩冶 王泽鸣 柴宝华

(1 天津大学 先进内燃动力全国重点实验室,天津 300350)(2 天津大学 机械工程学院,天津 300350)(3 中国原子能科学研究院,北京 102413)

近年来,我国在空间探测方面取得飞速进展,月球探测工程、火星探测工程都取得了显著成果,正在不断迈向“一百年一百个天文单位”的目标。空间探测任务要求能源系统具备较高的功率密度、稳定性和长寿命,核能在这方面具有独特优势,因此空间核电源被认为是执行长周期航天任务的首选能源之一,可为航天器提供高效的可持续能源[1]。自20世纪提出空间核电源概念以来,国内外已对空间核电源系统进行了诸多探索。20世纪末期,美国研发了30kW及400kW热管动力系统反应堆(SAFE-400)[2],到2015年,其新一代千瓦级空间核反应堆(Kilo-Power)已能够满足科学研究和空间探测任务的需求[3]。苏联/俄罗斯自20世纪中期开始空间核反应堆技术研究,先后开发了多种不同型号的千瓦级和兆瓦级核反应堆等空间电源,其中TOPUZ-II更是经过了14000h的整机考验[4]。在实际应用中,空间核电源系统面临着复杂的工程挑战,热管理便是其一。反应堆或动力循环系统产生大量的热或废热,必须有效地传递、排散和控制,以确保系统温度在适宜的范围内,防止过热,从而保障整个系统的安全和性能。文献[5]中提出核电源系统的稳定运行要求系统有足够的传热安全裕度,能够将反应堆堆芯裂变热及时导出,并对热管反应堆进行了堆芯安全分析。文献[6]中通过核热力计算表明,热膨胀造成堆芯边通道的中子泄漏增加,同时边通道中子泄漏增加加剧了功率分布的不均匀性,传热恶化。文献[7]中研究表明,对空间核电源辐射散热器的翅片进行优化设计可以有效提高辐射散热器的散热效率。热管作为导热元件,具有出色的热管理性能,可为核电源系统的设计和运行提供关键支持。依靠热管内工质的相变潜热吸收热源的热量,通过管内工质的相变流动循环将热量轴向导出。热管正常运行时,内部工质不断发生液相和气相的相互转换,工质处于饱和状态,具有极高的热传导特性和良好的等温性能,能快速完成热量传递。因此,热管在空间核电源系统的反应堆堆芯导热、核废料冷却、余热废热排放和安全裕度保护等方面具有广泛的应用[8]。

热管内冻结沉积是一个典型的固液相变过程,而当前对管内冻结沉积的研究尚处于空白阶段,大多数研究只针对热管的启动或调节过程。热管工质对热管性能有着极大的影响,文献[9]中根据应用需要选择合适的工质加工中温热管,并通过试验验证了其在500～700K的工作性能;此外,还发现芯钾热管的启动性能优于无芯钾热管[10]。文献[11]在钠热管的试验中发现在启动初期最可能遭遇夹带极限,启动末期可能遭遇毛细极限,解冻启动存在最低加热功率。文献[12-13]中的研究表明,倾角、充液量、热管比例及表面加工粗糙度等对热管的传热性能也具有较大影响。水热管主要用于低温区的传热工作,可满足航天器的低温区工作需求。千瓦级核反应堆堆芯产生的热量通过一系列高温钠热管转移到斯特林转换器的热端,斯特林转换器冷端余热通过钛-水热管转移到散热器面板,最终排放到太空环境中[14]。文献[15]中开发了钛-水热管,利用高温氧化着色法处理不锈钢表面,将热管的应用温区拓展到100 ℃以上,可用于100～300 ℃的温区,对未来的中高温区的航天器热排散系统具有重要的实用价值。

热管在偏离设计工况(尤其是低功率工况)下运行的冻结沉积现象,其形成过程及机制目前尚不明确,可能造成热管内工质的质量迁移,从而形成永久失效的运行路线,更未有研究涉及。为此,本文以水热管为研究对象,建立热管内气液固三相流动传热过程的数值模拟方法,研究低功率工况下热管内部工质流动特性与相分布规律,分析低功率状态下热管的运行机理和冻结沉积过程,并讨论冻结沉积现象发生时热管的流动与传热特性。本文研究可对热管的长期稳定运行设计提供参考依据,为空间探测器的稳定运行保障提供科学参考。

1 研究对象与方法

1.1 研究对象

在设计工况或接近设计工况下,热管蒸发段的吸热功率在额定功率附近,内部进行完整的气液相变循环过程,可保证在高负荷工况下长期稳定运行。然而,在空间探测任务中,航天器的大多数设备在飞行中处于休眠状态,因此热管经常在低于甚至远低于设计工况下运行,即蒸发段输入功率远低于额定功率。在该条件下,热管冷凝段仍保持较高的散热能力,使得冷凝段远离热端的部分温度急剧下降,直至冷凝段远端温度下降至热管工质的熔点以下,导致部分工质经由气-液-固过程而凝固,在局部形成冻结沉积而无法回流至蒸发段(如图1所示),最终有效工质减少,蒸发段回流不足甚至烧干,导致热管失效。考虑到热管结构高度对称,使用2维简化模型进行模拟,以提高计算效率。考虑到316不锈钢与水工质间的相容性,二者间会发生化学反应产生不凝性气体——氢气,因此本文中的不锈钢管壳和丝网芯经过了高温氧化处理,使其表面形成一层致密的氧化层,以避免与水工质的直接接触导致不凝气体的产生。本文研究热管的相关特性见表1。

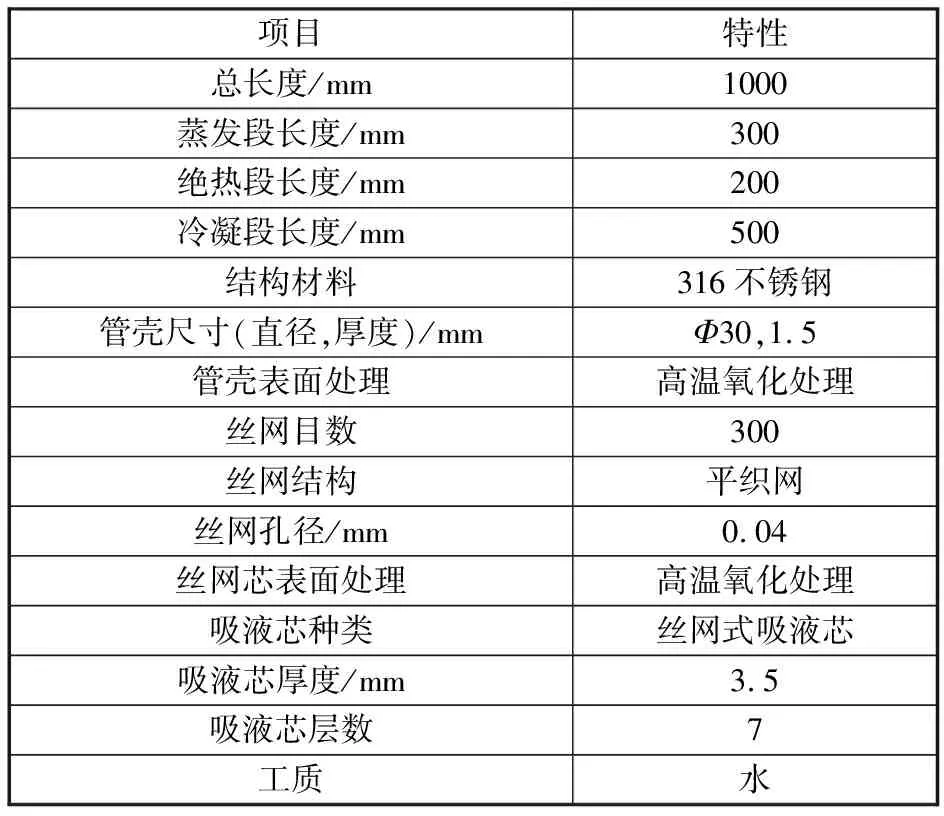
表1 热管特性

图1 热管及冻结沉积示意

本文计算中,使用水作为工质,3种相态随温度变化的热物理性质依据国家计量标准数据库(NIST)给出。

1.2 数值模型

数值计算采用流体体积(VOF-LEE)模型模拟管内相变流动,使用多孔介质模型处理丝网芯结构,采用凝固-融化模型计算工质的冻结沉积过程,引入吸液芯毛细力模型描述管内吸液芯驱动力。

1.2.1 VOF模型

在每个控制容积内,气相的体积分数αv和液相的体积分数αl的总和为1,即在相变的气液两相流中可得

αl+αv=1

(1)

通过求解容积比率连续方程完成相变界面追踪,方程如下。

式中:ρl和ρv分别为液相和气相的密度,kg·m-3;υl和υv分别为液相和气相的实际速度矢量的矩阵表示,m·s-1;Sαl,Sαv分别为液相和气相的相变质量源项,kg·m-3·s-1。

1)动量方程

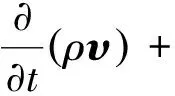
∇·[μ(∇υ+∇υT)]+F

(3)

式中:ρ为流体密度,kg·m-3;p为压强,N·m-2;μ为流体动力黏度系数,Pa·s;υ为流动速度矢量的矩阵表示,m·s-1;F为单位体积流体所受表面张力的矩阵表示,N·m-3。

2)能量方程

(4)

式中:E为控制体的比能,见式(5),J·kg-1;k为有效导热系数,W/K;T为温度,K;Q为相变能量项,W·m-3。

式中:El,Ev分别为液相和气相的比能,见式(6)和式(7),J·kg-1。

式中:cp,l为液相的定压比热容,J·kg-1·K-1;Tl,Tref分别为液相和相变温度,K。

式中:cp,v为气相的定压比热容,J·kg-1·K-1;Tv为气相温度,K。

3)质量传递

相变过程中,若控制体温度大于饱和温度,则有蒸发或沸腾过程,质量由液相传递到气相;若控制体温度小于饱和温度,则是冷凝过程,质量由气相传递到液相。其控制方程可表示为

式中:S为质量传递过程质量源项;Tsat为相变温度,K;γl,γv分别为与蒸发和冷凝相关的传质系数,默认数值0.1,对实际的气液相变工作过程可以按需进行调整,以与实际工作过程吻合。

4)能量传递

由式(8)得到的质量源项乘以对应压力条件下的汽化潜热,即可得到相间的能量传递为

Q=L·S

(9)

式中:L为汽化潜热,kJ·kg-1。

1.2.2 多孔介质模型

本文研究的对象为丝网吸液芯型热管,热管实物的吸液芯结构复杂,将吸液芯结构视作多孔介质进行处理,在模拟设置时给出对应几何模型的渗透率、孔隙率及流动阻力系数即可完成多孔介质流动设置。

多孔介质的孔隙率εw和渗透率K计算如下。

式中:sw为圆管内丝网吸液芯的卷绕系数,取1.05;N为吸液芯丝网目数;d为网丝直径。

多孔介质流动模拟需要定义各个方向上的阻力系数,即

式中:Si为i方向的动量源项;vi,vj分别为i和j方向流体流动速度矢量,m·s-1;Dij,Cij分别为黏性阻力系数矩阵D和惯性阻力系数矩阵C中的元素,分别表示黏性阻力损失和惯性阻力损失。

当多孔介质具有良好的均匀性时,可得

多孔介质区域的有效导热系数记为keff,由液相的吸液芯材料导热系数组合计算得到

式中:kl,ks分别为液相与固相的导热系数,W/K。

通过适当调整黏性阻力系数可以得到目标流动特性,在热管吸液芯中,液体流动以层流为主,惯性阻力损失通常可以忽略不计。

1.2.3 凝固融化模型

液固相变过程采用焓-多孔介质(Enthalpy-porosity)法来求解,在整个计算域内将液相体积分数离散到每个计算单元内。在热平衡的基础上,液相所占的百分比通过反复迭代求解,从而计算出液相实际所占的百分比。当控制体内液相体积分数为0时为固相,介于0～1时为糊状区,为1时为液相。

凝固融化问题的能量方程为

(15)

式中:H为工质的焓;Se为能量源项。

焓H通过显焓值h和潜热ΔH来计算。

H=h+ΔH

(16)

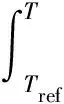
(17)

式中:href为参考焓;Cp为定压比热容。

ΔH=βL

(18)

式中:β为液体分数;L为汽化潜热。

1.2.4 吸液芯毛细力模型

在空间应用环境下,吸液芯提供的毛细力fc是管内相变流动循环过程的唯一驱动力,其与工质的表面张力系数σ、吸液芯有效半径rc和接触角θ有关。

表面张力系数和接触角为温度的函数,则热管的毛细驱动力可表示为

将式(20)对温度和横坐标X微分变形,得到与坐标X相关的毛细力表达式为

(21)

在数值计算中,数据取自计算域网格点,rc与吸液芯结构有关,与温度无关;工质的表面张力系数及接触角随温度的变化规律可由工质物性获得,∂T/∂X可以由网格域迭代计算时获得。

1.3 数值计算设置

在数值模拟中,通过用户自定义函数(UDF)将式(19)所表达的毛细力以动量源项形式引入,计算采用Realizablek-ε湍流模型进行流动模拟。边界条件设置中,蒸发段和冷凝段均设定为恒定热流边界,其他边界采用绝热壁面。

2 结果与分析

本文对水热管在设计工况和低功率工况下的相变流动过程进行数值模拟研究,拟定的模拟工况及相应计算设置如表2所示。

表2 数值模拟工况

2.1 设计工况运行特性分析

设计工况下,热管可以依靠管内相变流动循环过程将蒸发段输入的热量悉数传递至冷凝段排出。此时,管内的液相和气相分别在热管吸液芯和蒸汽腔内流动(见图2),气液界面并非平整表面,而是存在液面波动,这是因为蒸汽与液体反方向流动,使得蒸汽与液膜表面存在剪切作用。在某些条件下,当蒸汽流速过快时,这种剪切作用可能撕裂液膜表面,将液体从吸液芯中带出,与蒸汽一起在蒸汽腔内流动,此时热管遭遇夹带极限。图3为稳定运行时的流场分布。因为蒸发段温度较高,蒸汽形成后经过再次加热,在绝热段内处于较高的温度状态,因此流速较高;同时,蒸发段端部也出现了较高的流速,这是液体回流终点的流动端部效应导致的。在温度分布上,热管内温度由蒸发段向冷凝段温度依次降低,同时在径向呈现对称性分布(见图4),这与无重力条件下热管的实际工作过程相符。热管的壁面温度沿轴向降低,整体轴向温差不超过3K,具有良好的等温性(见图5)。温差主要与吸液芯内液体温度有关。热管蒸发段为热输入条件,冷凝段为输出条件,吸液芯内的液体在毛细力驱动下回流至蒸发段时,液体边回流边吸热升温,与此同时,内部流向冷凝段的高温蒸汽与回流液体间存在热量交换,使得液体吸收部分蒸汽热量,因此热管沿轴向温度降低的同时,径向上也存在微小的温度梯度(见图4)。

图2 设计工况下热管内相分布

图3 设计工况下热管内流动速度矢量图

图4 设计工况下热管整体温度分布

图5 设计工况下热管轴向壁面温度分布

2.2 低功率工况运行特性分析

当热管在远离设计工况的低功率工况下长期运行时,蒸发段输入热量远低于冷凝段散热热量,使得冷凝段温度逐渐降低,甚至有可能降低到工质的熔点以下,从而使工质在冷凝段冻结沉积,无法返回蒸发段,导致热管相变流动循环遭到破坏,最终导致热管失效。

本文重点关注相分布特性和温度分布特性。如图6所示,在低功率工况下,热管冷凝段的温度逐渐降低,某时刻(20438s)后,局部温度降至工质的熔点以下,且随时间进一步降低,凝固区域逐渐扩散至冷凝段末端。在计算时间内,轴向温差从稳定运行时的3K一直增大到75K(21180s),不再保持等温性能。图7为低功率工况下热管内的固相分布对应冷凝段发生冻结随时间的变化情况。冻结沉积向冷凝段末端发展,直至完全堵塞(如图8所示)。在这种情况下,冻结沉积导致热管内参与流动循环的工质严重不足,工作循环受到破坏,最终蒸发段烧干,热管不再保持良好的等温性能和传热能力,热管失效。此外,在吸液芯内的水工质低温冻结过程中可能存在膨胀效应[16],自然界中在岩石裂隙里的水体结冰时体积膨胀约9%,可产生约96MPa的高压,使原有的岩石裂隙扩大;而在热管的吸液芯内的多孔介质流动中,水的冻结将同样产生极大压力,破坏原有的吸液芯结构,导致网丝间隙增大甚至断裂,严重影响毛细力驱动液体回流,使得热管功能遭到破坏。热管的冻结失效将导致其参与的系统整体失效,应用于航天器散热时,会导致航天器热管理无法满足工作需求,航天器无法正常工作,最终导致任务失败。

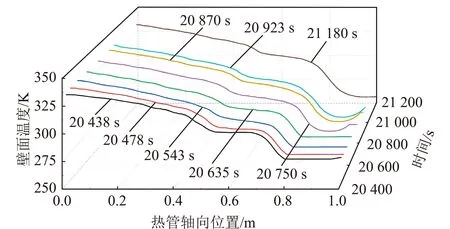
图6 低功率工况下热管轴向壁面温度分布

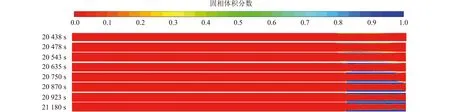
图7 低功率工况下热管内固相分布

图8 冷凝段冻结沉积放大图

3 结论

本文通过引入吸液芯毛细力源项的数值模拟方法,对水热管在设计工况下和低功率工况下的运行过程进行数值模拟研究;初步建立了热管内冻结沉积现象的数值模拟研究方法,对热管的长期稳定运行具有重要意义。相关研究内容可为航天器热管理的稳定保障和空间探测任务的成功稳定运行保障提供重要科学参考。具体结论如下。

(1)以水热管为例,建立热管气液固三相相变流动传热的数值模拟方法,用于描述低功率运行时热管内凝固、融化及气液相变过程。

(2)当热管在设计工况下工作时,蒸汽与液膜表面存在剪切作用,可能会撕裂液膜表面造成液体夹带。热管的温度沿轴向降低,轴向最大温差不超过3K,具有良好的等温性。

(3)在长期低功率工况下运行时,热管冷凝段温度会降低至工质的熔点以下,工质在冷凝段冻结沉积。热管不再保持良好的等温性能和传热能力,轴向传热温差逐渐增大,热管失效。