黄河流域黏性泥沙群体沉速计算分析

丰 青，肖千璐，郑艳爽，张晓华

(1.北京大学 环境科学与工程学院，北京 100084； 2.黄河水利委员会黄河水利科学研究院，河南 郑州 450003)

泥沙颗粒沉降特性是泥沙运动力学研究的关键基础问题之一。与单颗粒泥沙沉降不同，泥沙颗粒群体沉降特性受到泥沙级配组成、水流含沙量及颗粒相互作用等的影响[1]。黄河流域跨越多种地貌单元和气候带，黄河泥沙具有来源广、沙量多的特征。根据黄河泥沙不同来源区颗粒级配分析结果可知，泥沙颗粒级配由小于0.005 mm 到1.000 mm 连续存在，河道中不同颗粒组成泥沙的水沙动力特征差异较大[2-3]。王兆印等[4]对黄河干支流泥沙进行野外采样分析，认为黄河流域泥沙中矿物成分及含量是影响水体中悬浮颗粒流变特性的主导因素，黏性矿物含量对高含沙水流流变特性及沉速的影响比粒径分布的影响更大；另一方面，泥沙在河道中发生沿程分选，挟沙水流中悬浮泥沙沉降表现出显著的非均匀泥沙沉降特征，且不同含沙量及不同矿物组成条件下泥沙沉降规律可能发生变化[5]。这表明仅考虑泥沙粒径变化不能准确反映黄河流域泥沙的动力学效应，还应充分考虑泥沙矿物组成尤其是黏性沙矿物组成及含沙量的影响。水体絮凝结构的形成与水体内泥沙颗粒pH 值和盐度直接相关[6]，考虑到黄河流域干支流非感潮河段的水体和土壤基本呈碱性，在含沙量不是特别高的条件下基本无法形成絮凝态结构[7]。因此，在进行黄河流域泥沙颗粒群体沉速研究过程中，需主要考虑挟沙水流黏性特征及含沙量的影响。

国内外学者采用试验研究和理论推导等方法围绕挟沙水流中含沙量对泥沙颗粒群体沉速影响开展了深入研究，提出了不同类型的泥沙颗粒群体沉速计算公式[8-9]。沙玉清[10]以体积含沙量Sv=0.3 为临界值，考虑不同流区阻力系数和雷诺数关系变化，建立了泥沙颗粒群体沉速分段表达式；窦国仁[11]引入泥沙颗粒雷诺数对泥沙颗粒尾流产生的形状阻力进行分析，推导了含有泥沙颗粒沉速的尾流形状阻力表达式，采用该式求解沉速需要进行较复杂的迭代试算；郜国明等[12-13]采用深度取样锥形筒流态化法开展了非均匀泥沙群体沉降速度试验研究，建立了包含悬沙浓度、中值粒径及非均匀性系数的泥沙群体沉速表达式。上述研究多适用于非黏性泥沙，而黄河流域泥沙来源区中的泥沙多含黏性矿物成分，特别是黄河中游砒砂岩区的红色砒砂岩富含蒙脱石，具有较强的水溶性和膨胀性，泥沙颗粒群体沉降规律与非黏性沙明显不同。通过野外采样分析可知，该类泥沙中值粒径小于0.05 mm，但在实验室静态水体沉降过程中并未形成明显的絮凝结构。在天然暴雨产流条件下，红色砒砂岩溶于水后会明显提升水体黏滞性，造成泥沙沉降特性及含沙水流特别是高含沙水流输送特性发生显著变化，低含沙水流条件下的泥沙群体沉速计算方法不再适用，需进一步考虑挟沙水流黏性和紊动特征变化对泥沙颗粒沉降过程中能量耗散的影响。本文从泥沙颗粒沉降过程的受力分析出发，考虑泥沙颗粒沉降引起的运动黏性切应力和紊动黏性切应力的影响，引入水流综合黏性系数，建立反映水流黏性及颗粒阻力特征影响的泥沙沉降速率表达式，并采用黄河流域典型黏性泥沙红色砒砂岩颗粒开展泥沙群体沉速试验对构建公式进行验证分析，可为黄河流域黏性泥沙淤积和输移规律研究提供参考。

1 泥沙颗粒沉速理论分析

针对挟沙水流中含沙量对水流黏性及泥沙沉降模式的影响，张红武等[14]基于水沙两相连续性假定提出在固定单位水柱内，泥沙颗粒沉降将引起同体积水体向上运动，根据质量守恒定律，有：

式中：Sv为体积含沙量； ω为泥沙群体沉速；Vup为泥沙颗粒运动速度。根据式（1）可得：

当Vup为定值，假设Sv=0 时，有 ω=Vup=ω0，其中 ω0为清水中的泥沙颗粒沉速。考虑含沙水体黏性变化，张红武等[14]提出泥沙群体沉速计算公式如下：

式中： ν0为清水运动黏性系数； νm为浑水运动黏性系数；n3为系数。张红武等[14]采用实测数据对上式进行率定计算，推荐采用n3=3.18。

通过欧拉和拉格朗日不同参照物对比分析和泥沙颗粒的受力分析，泥沙颗粒在下沉过程中，其下部水体和侧面水体不断补入泥沙颗粒原有位置。试验结果表明，泥沙颗粒下落过程中其尾部可能出现负压区域但未出现真空区域。考虑到泥沙颗粒具有双电层结构，下落过程中补充进入原位置处的水体密度仍为自由水密度，并非束缚水内的高密度状态。以水体内固定位置处为参照物，根据动量守恒定理，也能获得式（1）形式的表达，但经过泥沙颗粒运动状态及受力特征分析可知，速度Vup并非为定值，即使在清水条件下，泥沙颗粒粒径差异和泥沙颗粒沉降过程引起的尾流强度变化导致置换水体运动速度有所不同。若以泥沙颗粒及其置换水体为参照物，当泥沙颗粒下沉过程中进入稳态，即泥沙颗粒水下有效重力等于阻力时，根据能量守恒定律，单位长度内泥沙颗粒损耗的势能除转化为泥沙颗粒的动能外，泥沙颗粒下沉速度与置换水体之间的速度差被泥沙颗粒周围的黏性切应力摩擦消耗。若以水面或河床床面为参照物，泥沙颗粒沉降过程的能量耗散可采用下式表达：

式中：D为混合沙代表粒径，在进行泥沙群体沉速计算中一般取中值粒径； ρ为水体密度； νΣ为水流复合黏性系数，为运动黏性系数和紊动黏性系数的耦合值，在泥沙颗粒沉降过程中未出现边界层分离诱发的紊流阻力情况下可取运动黏滞系数 νm；当泥沙颗粒出现边界层分离时，清水条件下单颗粒泥沙可通过窦国仁采用的分离角试验结果确定水流复合黏滞系数的阈值[15]；而浑水水流泥沙颗粒之间由于具有较强的相互作用，复合黏滞系数不易通过单颗粒沉降分析获取，大多采用室内试验率定的方式确定其数值。实际上，ρνΣ∂Vup/∂n为作用于泥沙颗粒表层的黏性切应力，流速梯度方向经过泥沙颗粒的重心。根据泥沙颗粒侧向摩擦的物理图形，可将 ∂Vup/∂n进一步表示为：

将式（5）代入式（4）并积分，有：

式中：c2为积分常数。泥沙颗粒在水体沉降过程中，考虑最小的泥沙颗粒不能小于泥沙颗粒的薄膜水厚度，即极限情况下的厚度值为薄膜水厚度，此时有：

式中： δ为泥沙颗粒薄膜水厚度。联立式（3）与式（7），则可获得考虑泥沙颗粒沉降引起的黏性切应力变化的沉降速度表达式：

式（8）中含沙水流黏性系数 νm可采用费祥俊[16]提出的黏性系数公式进行计算，泥沙颗粒薄膜水厚度采用韩其为[17]推荐的数值 δ=4×10-7m 进行计算。浑水运动黏滞系数 νm的计算式为：

式中：Svm为极限体积比含沙量；Pi和Svm分别为某一粒径级的平∑均直径及其相应的质量百分比。假设各粒径级泥沙密度差异不大，则质量百分比约等于体积百分比，式中可理解为混合沙单位质量泥沙比表面积的一种表达形式。

2 泥沙颗粒沉速试验

试验装置采用定制的搅拌式沉降桶，沉降桶高2.0 m、内径1.0 m，搅拌桶底部安装三叶倾斜剪切桨进行含沙水体的掺混搅拌，外部由变齿变频电机提供搅拌动力。搅拌桶上部设置加筋环，以增强搅拌桶的侧向稳定性，上部固定十字测架，在测架上焊接挂架并将测量设备固定于挂架底端（图1），测量设备可沿径向和垂向移动。试验过程中，根据各测点空间位置操作挂架沿滑道完成指定距离的移动，并进行对应时间的含沙量测量。

图1 搅拌筒上置十字测架和仪器挂架Fig.1 The configuration of cross measuring frame and instrument pylons

泥沙颗粒群体沉速试验采用Campbell Scientific 公司生产的OBS 3+浊度仪和CR1000 型数采控制器测量含沙量，通过控制挂架的伸缩长度完成系列点位的含沙量测量。正式试验前开展了不同含沙量条件下OBS 3+浊度仪标定试验，结果如图2 所示。

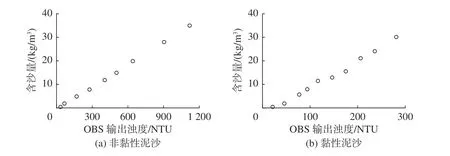
图2 非黏性泥沙（花园口沙样）和黏性泥沙（红色砒砂岩）含沙水流浊度值与含沙量标定Fig.2 Calibration diagram for OBS 3+ probe in non-cohesive sediments (sampled at Huayuankou) and cohesive sediments (red Pisha sandstone) within sediment-laden flow

试验中黏性泥沙采用黄土高原鄂尔多斯南部乌兰木伦河上中游滩岸处的红色砒砂岩，并同时取黄河下游花园口河段汛后滩面的非黏性泥沙作为对比研究。测定黏性泥沙中值粒径为0.044 mm，沙样涵盖各粒径的泥沙颗粒，级配曲线连续性明显且较为平缓，具有显著的非均匀特征；采用X-射线荧光光谱仪测定黏性泥沙矿物成分，结果表明蒙脱石质量占比接近50%，其他成分为石英、斜长石、钾长石等非黏性矿物。考虑到河道中水流含沙量特征及浊度仪测量含沙量的有效量程，试验中沉降桶含沙水体各组次垂向平均含沙量分别设置为2.0、6.0、12.0、16.0 kg/m3。

试验时先将清水注入搅拌桶直至液面距搅拌桶底高度1.2 m，再加入提前称重的试验用沙，启动剪切桨片充分搅拌，确保桶内水沙混合均匀。随后关闭搅拌机，在桶内水体旋转基本停止后开始测量桶内含沙量垂向分布，测点垂向间距0.1 m，测量时间间隔3～5 min。每组次试验开始前先进行搅拌桶清理，以降低不同类型泥沙混合引起的试验误差。

根据各试验组次不同时刻含沙量垂向分布测量结果，对泥沙群体沉速变化规律进行分析。为反映不同含沙量条件下沉降桶内泥沙沉降规律，以平均含沙量为2.0 kg/m3和12.0 kg/m3组次为例，分析含沙量变化对不同时刻沉降桶内含沙量垂向分布及沉降特性的影响。由图3 可见，在测量开始阶段，垂向含沙量差异较大，且含沙量较低时垂向分布更不均匀；随着时间的推移，含沙量变化速率逐渐减缓，低含沙量条件下浓度减缓速率大于高含沙条件，泥沙颗粒群体沉速逐渐趋于稳定值。根据试验测得的非黏性泥沙和黏性泥沙不同时刻含沙量垂向分布数据，采用麦克劳林公式计算不同沉降时间内不同水深处泥沙群体瞬时沉速，断面平均沉速取含沙量达到初始含沙量50% 时的沉降时间内的沉速平均值。以黏性泥沙平均含沙量为16.0 kg/m3的组次为例，计算不同水深处沉速和断面平均沉速，结果见表1。若以最底层泥沙群体沉速作为该试验组次的泥沙群体沉速，计算表明含沙量为16.0 kg/m3条件下泥沙群体沉速为0.014 6 cm/s。

表1 垂向平均含沙量16.0 kg/m3 组次黏性泥沙群体沉速Tab.1 Calculated settling velocity of cohesive sediment group for sediment concentration 16.0 kg/m3

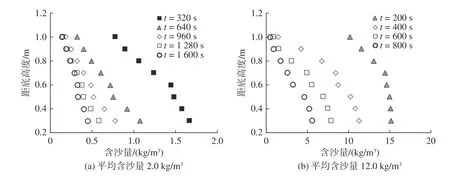
图3 不同含沙量条件下不同时刻沉降桶含沙量垂向分布Fig.3 Variations in sediment concentration profiles at different time intervals with varying average sediment concentrations

由试验结果可知，红色砒砂岩组成的含沙水体中泥沙群体沉速整体随含沙量增加而减小并逐渐趋于定值，而当平均含沙量为0.34～0.45 kg/m3时，泥沙群体沉速出现随含沙量增加而增大的现象。分析试验过程中泥沙颗粒垂向分选变化过程，当含沙量较低时，水流黏性仍可保持与清水相似特征，泥沙颗粒的分选作用使得沉速较大的泥沙群集中于含沙量较大的近底处，造成含沙量较大的区域出现泥沙颗粒群体沉速较大的反常现象。这说明含沙量很低的条件下，泥沙颗粒非均匀特征伴随的各粒径沉速垂向分选未体现泥沙群体特征，仅表现出各粒径颗粒混合沉降的综合统计结果。随着含沙量的增加，泥沙颗粒对水流黏性影响及颗粒间的相互作用成为制约泥沙颗粒群体沉速的主要因素。

3 泥沙沉速计算式验证

利用沉降试验获得的泥沙群体颗粒沉速数据对上文建立的公式进行验证。各组次泥沙颗粒群体沉速试验值与计算值对比见表2。

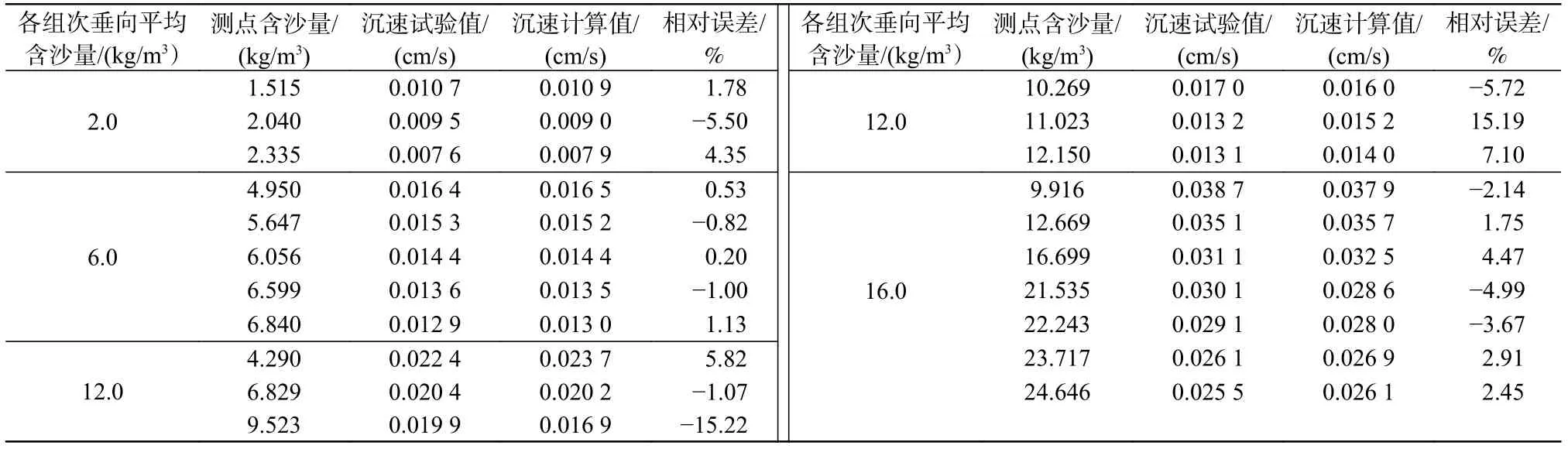
表2 泥沙颗粒群体沉速试验值与计算值对比Tab.2 Comparison between the experimental and calculated settling velocity of sediment particles

由表2 可见，式（8）考虑了水流运动黏性切应力和紊动切应力影响，能够更完整地反映泥沙颗粒群体沉降过程中的能量损耗程度，可较好地呈现黏性泥沙群体沉降规律。为区分泥沙颗粒沉降过程中非均匀性引起的垂向分选对验证分析的影响，以每组黏性泥沙沉降试验测点处浓度降至初始浓度50%的时间和含沙量变化计算泥沙群体沉速，并以此作为各组次不同含沙量对应的颗粒群体沉速数据。由于泥沙粒径垂向分选的影响，验证计算过程中需进行不同组次对应稳态泥沙粒径试算。先给定各泥沙粒径引起的水流复合黏滞系数初值，再利用垂向平均沉速确定各试验组次的水流复合黏滞系数。试验水体垂向平均含沙量分别为2.0、6.0、12.0 和16.0 kg/m3时，相应的水流复合黏滞系数为7.15、6.10、4.57 和4.35 mm2/s。可见，随着含沙量的增加，水流复合黏滞系数呈减小趋势。相同剪切速率条件下泥沙颗粒附近水沙界面处能量耗散强度逐渐减小，泥沙颗粒沉降过程中与向上运动的同体积水体之间相对位移有所减小。

4 结 语

针对黄河流域含有黏性矿物成分的黏性泥沙沉降特征进行分析，以泥沙颗粒为参照物进行了受力分析和能量损耗分析，建立了考虑挟沙水流运动黏性系数和紊动黏性系数的泥沙群体沉速显式表达式，并采用黄河流域典型黏性泥沙红色砒砂岩颗粒开展了泥沙群体沉速试验研究，得出主要结论如下：

（1）黏性泥沙进入水体不仅改变了水流的黏滞性，对泥沙颗粒水沙界面处的紊动剪切强度也将产生显著影响，黏性泥沙群体沉速降低是水流黏性、密度和能量耗散强度变化的综合表现。

（2）天然条件下黄河流域典型黏性矿物组成的黏性泥沙未出现显著的絮凝团结构，红色砒砂岩组成的含沙水体中泥沙群体沉速整体随含沙量增加而减小并逐渐趋于定值；当平均含沙量为0.34～0.45 kg/m3时，出现泥沙群体沉速随含沙量增加而增大的现象。采用试验数据对建立的公式进行了验证，公式能较合理地表达水流黏性和尾流分离对泥沙颗粒沉降阻力的影响。

（3）黄河流域黏性泥沙颗粒级配跨度较大，受试验条件限制泥沙沉降过程中可能出现垂向泥沙颗粒分选，对试验结果产生一定影响。天然河道中，经过一定距离的水沙界面交换，河道较强的沿程分选作用下悬沙级配在一定范围内较为稳定，此时泥沙群体沉降速度计算可采用不考虑悬沙颗粒垂向分选影响的结果。