分数一阶电路等效模型估计锂离子电池SOC

徐鹏跃,张国玲,王 涛,程 佳*

(1.沧州职业技术学院车辆工程系,河北 沧州 061000;2.河北工业大学机械工程学院,天津 300400)

在实际运行中,锂离子电池的内部状态无法直接测量,给电池管理系统(BMS)的设计带来很大的困难。为保证系统的高效、安全、稳定运行,BMS 要能准确地估计电池的状态,而使用更精确的模型参数是实现准确估计的前提[1]。

标准等效电路模型由一系列电阻和电容组成,常见的有Rint 模型、Thevenin 模型及各种并联RC 支路的电路模型,均为整数阶模型。近年来,由于分数阶理论的提出,且研究发现纯电容对应的电化学阻抗谱(EIS)与实际的电池动力学不完全一致,人们提出了包含恒相位元件(CPE)[2]的等效电路模型,并称为分数阶模型。分数阶模型对电池模型精度的影响很大,且与电池的荷电状态(SOC)有一定的相关性。梁莹等[3]比较了3 种一阶电池模型,评价了模型的准确性。文献[4]采用二阶电路模型对电池建模,结合扩展卡尔曼滤波(EKF)对SOC 进行估算,误差率在±5%以内。文献[5]在EIS 中对比了整数阶和分数阶模型,并采取分数阶联合卡尔曼滤波器对模型参数进行在线辨识,辨识结果稳定性高。

模型参数的准确性也至关重要。锂离子电池的参数识别方法的研究较多:文献[6-7]讨论了基于粒子群算法的方案,文献[8-9]研究了基于递推最小二乘(RLS)法的方案。其中,粒子群算法在参数识别中存在初始值随机、种群聚类、容易陷入局部最优、收敛速度慢等不足。RLS 法为一种在线辨识方法,近年来,基于遗忘因子的递推最小二乘(FFRLS)法日益频繁地用于辨识电池参数。

本文作者以磷酸铁锂锂离子电池为研究对象,采用整数一阶模型、整数二阶模型及分数一阶等电路模型,分别进行等效分析,使用FFRLS 算法辨识模型中的参数。采用EKF算法对电池SOC 进行估计并且输出矩阵为电池端电压,为判断模型精度提供数据支撑。

1 电池模型建立

1.1 整数一阶电池模型

整数一阶等效电路模型见图1。

图1 整数一阶RC 等效电路模型Fig.1 Integral first-order RC equivalent circuit model

该模型由电压源、电池欧姆内阻和一个RC 电路支路组成,其中:Uoc为电池开路电压;UL为电池的端电压;I为充放电电流;R0为电池欧姆内阻;R1、C1为极化电阻和电容;U1为电阻R1的端电压。

根据电路定理可以写出电路关系,如式(1)所示;电池SOC 根据安时积分法可定义为式(2)。

式(1)、(2)中:t为时域;Qn为电池额定容量。

参数辨识和SOC 估计均涉及离散状态空间方程,可将式(1)、(2)离散化后写成状态方程的形式[式(3)]。

式(3)中:k为离散域;T为采样时间;e 为自然底数。

1.2 整数二阶电池模型

整数二阶等效电路模型见图2。

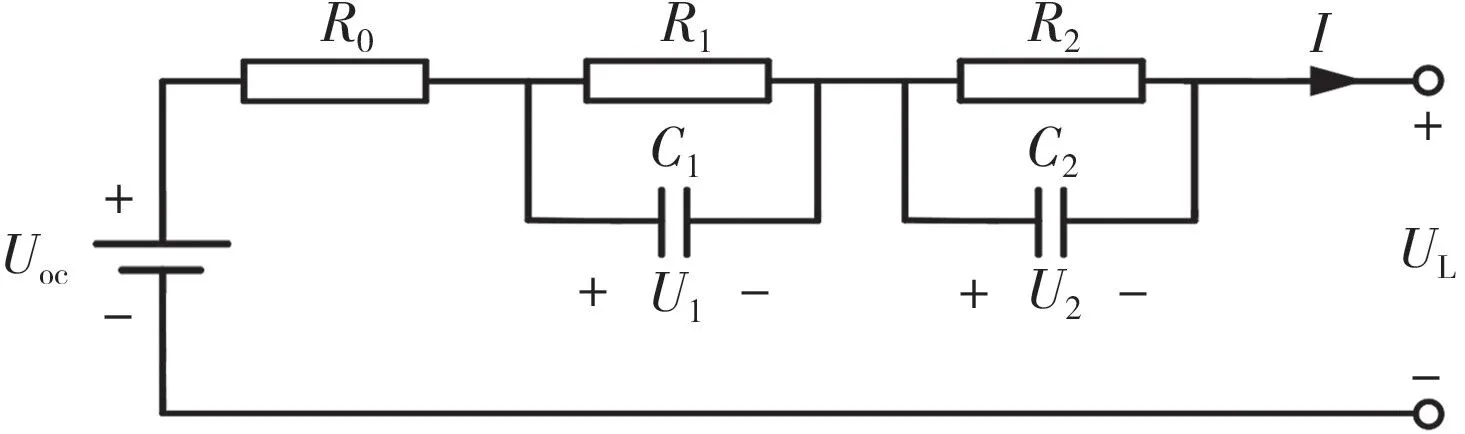
图2 整数二阶RC 等效电路模型Fig.2 Integral second-order RC equivalent circuit model

该模型比起一阶模型多一个并联RC 电路支路,理论上,精度会高于一阶电路模型精度,其中:R2、C2为浓差电阻和电容;U2为电阻R2的端电压。

列写电池等效电路关系,如式(4)所示。

写成离散化的状态空间方程形式,如式(5)所示。

1.3 分数一阶电池模型

分数一阶等效电路模型见图3。

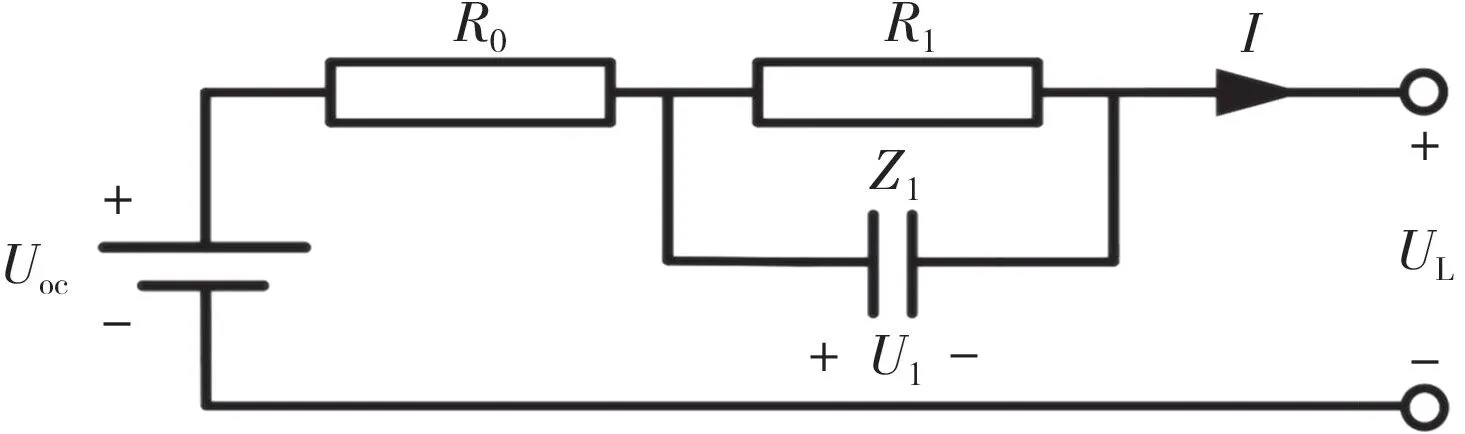
图3 分数一阶等效电路模型Fig.3 Fractional first-order equivalent circuit model

该模型相较于整数一阶模型引入了CPE,从而构成了分数阶等效模型,理论上,精度会高于一阶电路模型精度,其中:Z1表示恒相位元件。

CPE 定义为:

式(6)中:C为模型元件参数;α为CPE 的阶数,取值为[-1,1];ω为角频率;i代表虚部。

写出电路关系如式(7)所示。

分数阶微积分采用Grunwald-Letnikov 离散化方法进行计算,如式(8)所示。

2 在线参数辨识

在线参数辨识是在当前时刻采集到的数据基础上,对参数进行递归辨识的方法,为使数据更贴近真实的结果,辨识结果需要跟随系统的不同输入进行实时修正。

实验所用在线参数辨识方法为FFRLS 法,与传统的最小二乘法相比,实现了在线参数辨识的功能,降低了误差,并克服了RLS 法随数据量增大会出现数据饱和的问题。FFRLS法在RLS 法中引入遗忘因子,在递归过程中对新旧数据的权重进行重新分配,降低旧数据在递归结果中的占比,使算法能够快速收敛至真实值附近。

FFRLS 算法的步骤如下。

①定义φ(t)为观测矩阵,θ为参数矩阵,包含电路中的参数,如R0、R1、C1等。

②计算增益矩阵K(k+1)。

式(10)中:P(k)为协方差矩阵;λ为遗忘因子,λ≤1。

③更新协方差矩阵。

④计算误差矩阵e(k+1)。

式(12)中:y(k+1)为输出矩阵。

⑤更新参数矩阵。

⑥重复步骤②～⑤,直至在线参数辨识结束。

3 扩展卡尔曼滤波算法

EKF 和基于EKF 的自适应算法广泛应用于SOC 估计,基本思想是通过泰勒展开对方程进行线性化。算法中使用的非线性离散系统方程的一般公式见式(14)。

式(14)中:f(xk,uk)为非线性系统的状态传递函数;g(xk,uk)为非线性系统的测量函数;xk为第k步的状态向量;yk为系统的输出变量;wk为过程噪声;vk为测量噪声。

忽略式(14)中的高阶项,可得式(15)。

式(15)中:^xk为k时刻输出矩阵的预测值。

EKF 的详细计算过程如下。

①初始化x0,Q、R和P;其中,Q和R分别为噪声wk和vk的方差矩阵,一般用vk来估计R,vk在实验中得到,Q通常由经验设定,P为协方差矩阵。

②先验估计。

③更新端电压与先验估计端电压之间的差值ek。

④更新增益矩阵Kk。

⑤更新状态向量:

⑥更新协方差矩阵。

⑦重复步骤②～步骤⑥,直至SOC 估计结束。

4 结果与讨论

实验测试的电池为IFP36130155-36Ah 型磷酸铁锂锂离子电池(山东产),额定容量为36 Ah,工作电压为2.5 ～3.7 V,标准放电电流为12 A,最大充电电流为12 A。

在动态应力工况[10]下,对电池的参数以及SOC 进行估计,分数阶阶数α固定为0.5,参数辨识的结果见图4-6。

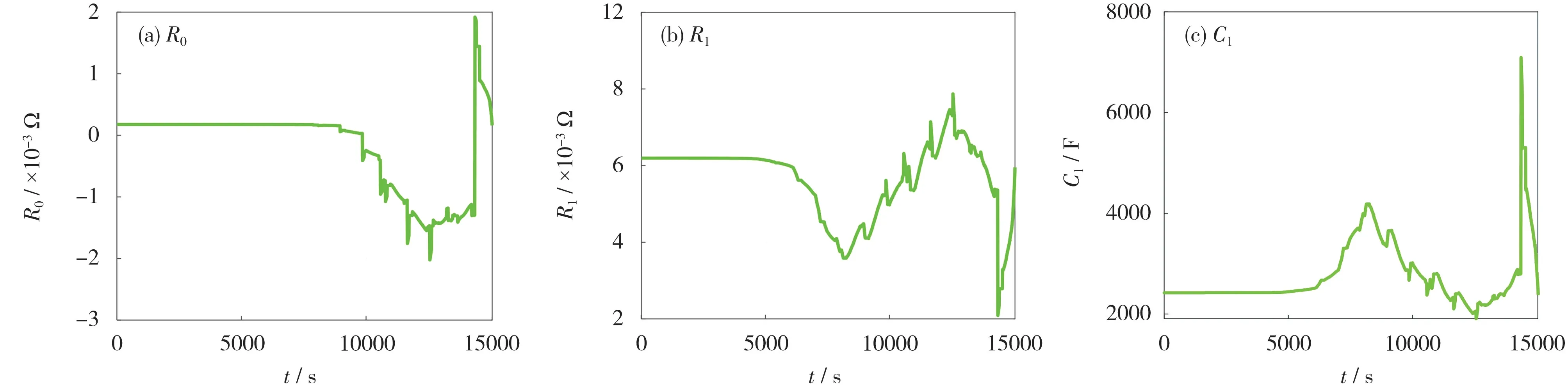
图4 整数一阶参数辨识结果Fig.4 Integral first-order parameter identification results

图5 整数二阶参数辨识结果Fig.5 Integral second-order parameter identification results

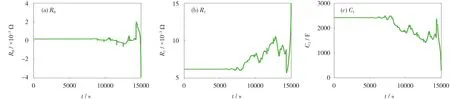
图6 分数一阶参数辨识结果Fig.6 Fractional first-order parameter identification results

从图4-6 可知,R0、R1和C1的辨识结果相差不大,根据理论分析,阶数存在于C1中,则C1大小存在偏差,结果符合理论逻辑。整数二阶由于增加了一个并联RC 支路,辨识的参数较整数一阶增加了R2、C2。由理论分析可知,并联的支路越多,并联的参数对电池的影响越小。读取R2、C2的数值发现,R2、C2的值小于R1、C1,符合理论分析。

3 种电路模型的预测端电压及真实端电压见图7。

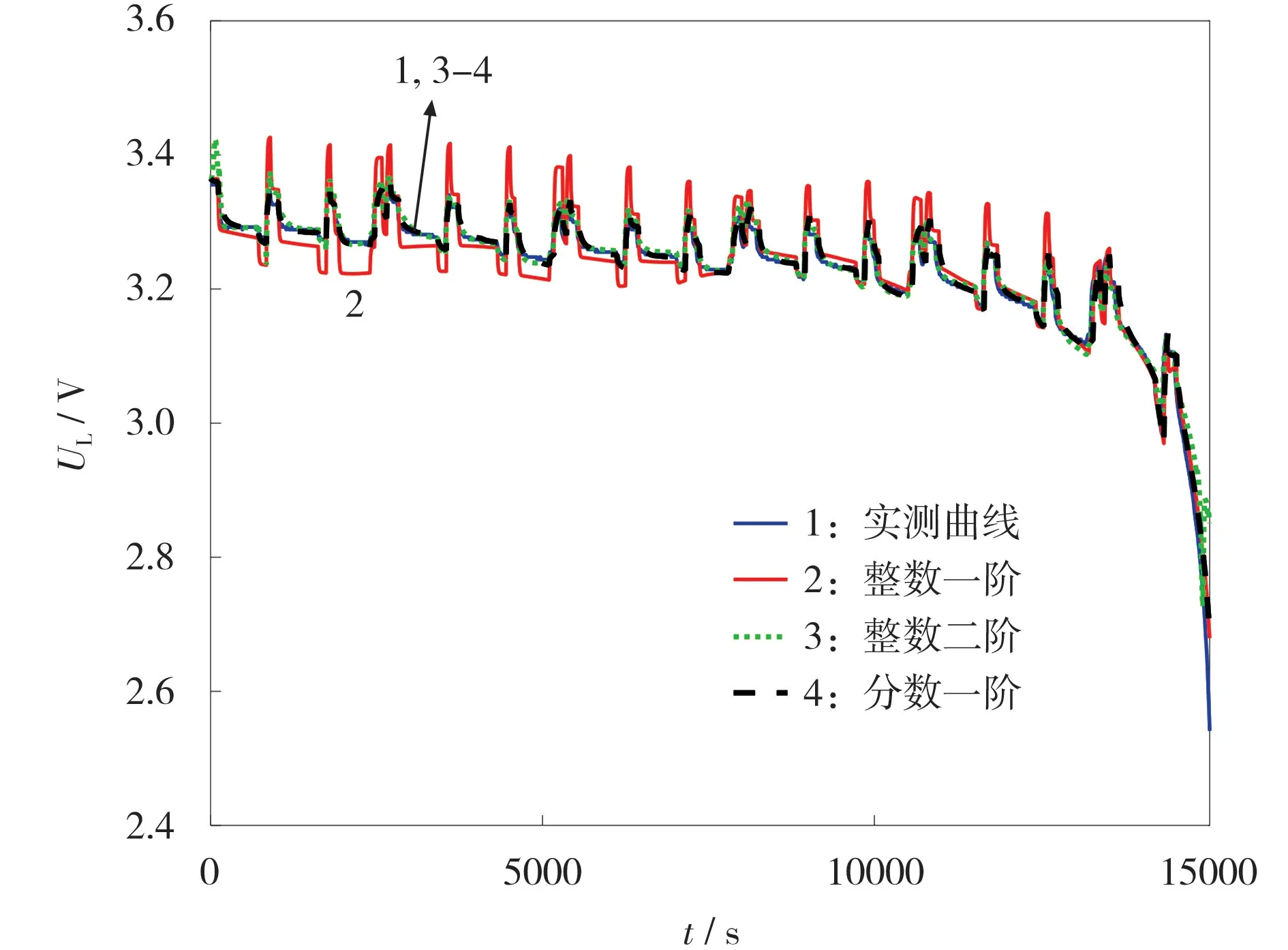
图7 3 种电路模型的预测端电压与真实端电压Fig.7 Predicted terminal voltages of three circuit models and real terminal voltage

从图7 可知,整数二阶曲线更贴近于真实端电压,原因是整数二阶电路模型精度高于整数一阶。此外,分数一阶电路模型比起整数一阶更贴近EIS,因此分数一阶电路预测端电压曲线会更接近真实端电压曲线。对比整数二阶和分数一阶的预测端电压曲线可知,二者的曲线接近程度近似,表明分数低阶电路可用更少的电气元件达到整数高阶电路的精度,简化了电路模型,也降低了计算量。

3 种模型的端电压误差曲线见图8。

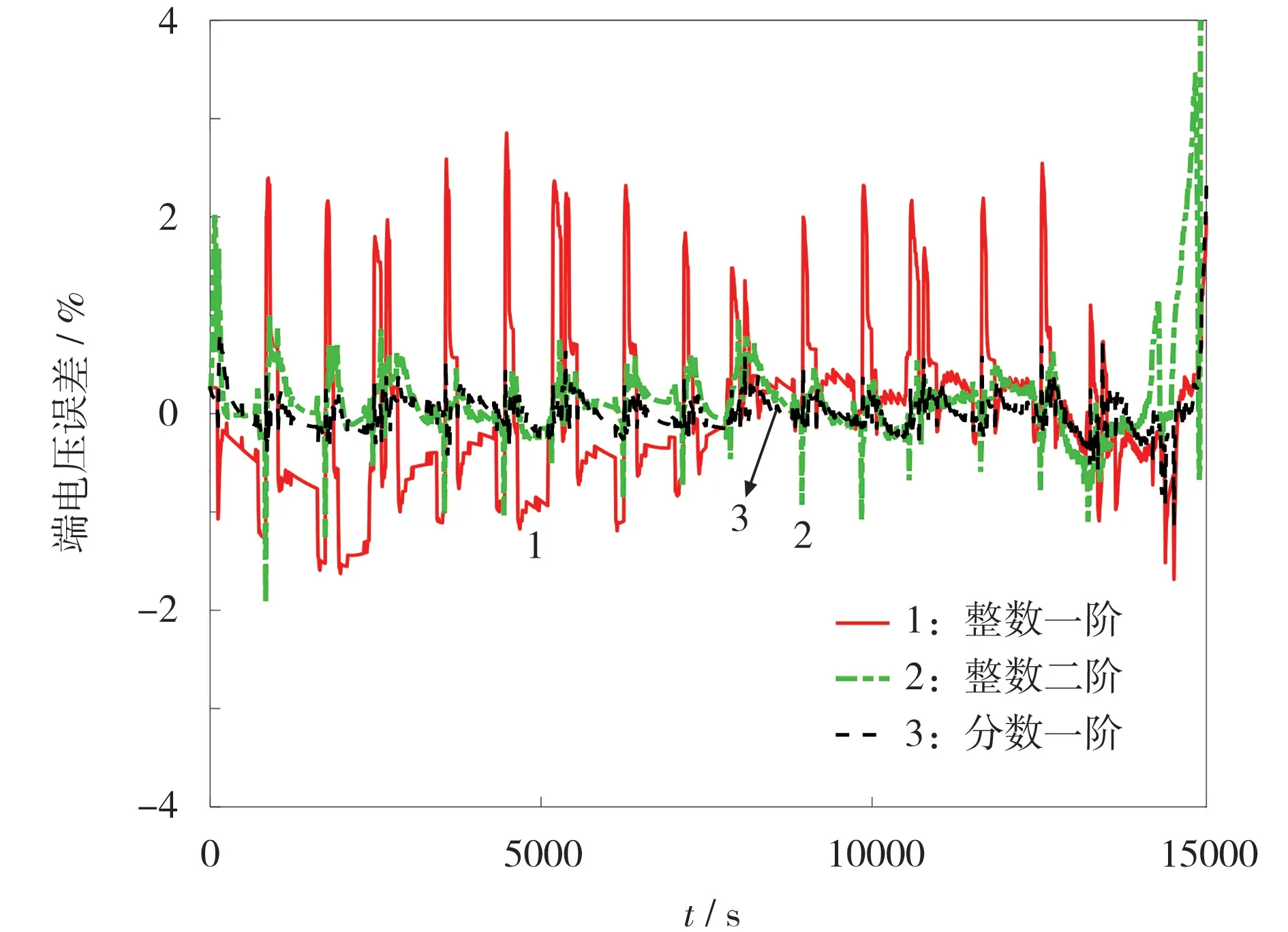
图8 3 种模型的端电压误差曲线Fig.8 Terminal voltage error curves of three models

从图8 可知,整数一阶的端电压误差远大于整数二阶和分数一阶的,而整数二阶和分数一阶的端电压误差相差不大,分数一阶的端电压误差略小于整数二阶,表明分数低阶的精度与整数高阶的精度相差不大,甚至会优于整数高阶电路模型的精度,体现了分数阶模型的优越性。

3 种电路模型的SOC 估计结果见图9。

图9 3 种电路模型SOC 估计曲线与实测SOC 曲线Fig.9 SOC estimated curves of three circuit models and measured SOC curves

从图9 可知,整数一阶模型的估计精度最差,整数二阶模型精度较好,分数一阶模型精度最好,验证了分数阶模型精度的优越性。

3 种电路模型的SOC 估计误差见图10。

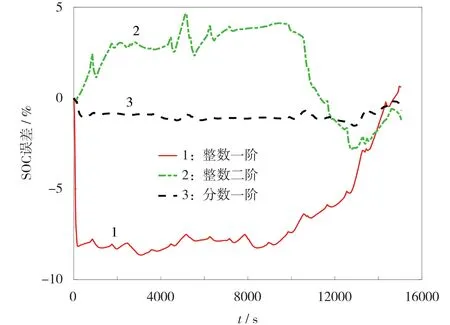
图10 3 种模型的SOC 估计误差Fig.10 SOC estimation errors of three models

从图10 可知,整数一阶模型估计SOC 的误差约为8%,整数二阶模型SOC 误差约为7%,而分数一阶模型的SOC 误差仅约为1%,分数阶模型下估计的SOC 误差小于整数一阶、整数二阶模型,体现了分数阶模型的有效性。

5 结论

本文作者以磷酸铁锂锂离子电池为研究对象,采用整数一阶、整数二阶及分数一阶等3 种电路模型对电池进行等效建模。对电路模型中参数进行在线辨识及SOC 估计,发现:整数阶模型中,阶数越高,模型的精度越高,体现在端电压误差及SOC 估计误差会随着阶数增加而减小;分数阶模型与整数阶模型相比,在阶数相同时,优于整数阶模型,在阶数不同时,精度足以媲美高阶整数模型的精度,甚至在某些情况下,低阶分数模型的精度会优于高阶整数模型的精度,体现了分数阶模型的有效性与优越性。