基于主动方波激励检测锂离子电池早期内短路

常 春,王瑛琦,姜久春*,吴铁洲

(1.湖北工业大学电气与电子工程学院,湖北 武汉 430068;2.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室,湖北 武汉 430068)

目前,对电池内短路的检测诊断方法可以大致分为3 个方向:终端电压和表面温度监测、泄漏特性气体的监测和电池内部状态监测等。前两种方向的诊断方法对电池早期内短路的识别并不是很敏感,且内短路至热失控排出的气体成分复杂,检测难度大。第3 种方向主要由内部参数、内阻和充电状态等3 种类型的参数组成。通过比较单只电池的参数和平均参数来隔离故障电池。这类算法可以嵌入电池管理系统(BMS)中,用于在线识别,因此,受到人们的广泛关注。M.G.Ouyang 等[1]提出采用递归最小二乘(RLS)算法来识别串联不同单元之间的内阻和荷电状态(SOC),以估算短路电阻。人们试图通过估计内短路(ISC)电阻来验证短路是否存在,同时跟踪短路的程度并计算短路电流引起的容量损失。在短路的初期阶段(也称为软短路),检测短路是非常棘手的,此时的短路对电池性能的影响非常轻微,因此特征很微弱。S.Bharathraj 等[2]提出一种诊断协议,采用小电流脉冲激励,专门用于在短路早期阶段检测短路。此协议基于一个简单的想法,即ISC 会导致电流泄漏,从而削弱电池的充放电能力,且泄漏电流的电荷量会在整个循环过程中累积。内短路电池与老化电池形成了对比,老化电池的容量本身由于退化而减少,内阻高于新电池,因此,可通过极限电流估计和实验测试极限电流来诊断ISC 故障。极限电流诊断电池内短路具有可行性,但这种估算与测试都很耗时。

本文作者提出一种通过简单的小电流激励获取电压响应来判断电池是否存在内短路的方法,建立短路程度与压升参数之间的联系,并讨论单体电池短路的阈值设置,研究电池组短路的判断标准。

1 实验

1.1 预实验研究

内短路电池的产生方式主要分两种:①在正、负极添加诸如铜之类的污染物。这种方法能很好地模拟内短路的实际情况,但内短路的开始时间点和程度无法控制。②在电池外部并联电阻来模拟内短路。这种方法能很好地控制内短路的开始时间点和程度,但与真实内短路内部的实际情况存在差异。实验选用第二种方法来模拟内短路电池[3]。

电池端电压在电流激励作用下将偏离开路电压,偏离量即为电池在该电流下的过电势,即动力学参数将直接影响电池在电流激励下的过电势。电池过电势由内部多个电化学过程共同影响,主要包括:①正负电极固相电子电流导致的欧姆过电势;②电化学反应电流通过负极颗粒表面固体电解质相界面(SEI)膜引起的欧姆过电势;③液相离子电流导致的欧姆过电势;④液相Li+浓度梯度导致的液相浓差过电势;⑤正负电极固液相界面处的电化学反应过电势;⑥固相Li+浓度梯度导致的固相浓差过电势。固相浓差过电势除与固相Li+浓度梯度有关外,还与开路电压曲线的斜率有关。在开路电压曲线平台区[即1C曲线峰或差分电压(DV)曲线谷],相同的浓度梯度将导致更小的固相浓差过电势,即在电压平台区,固相浓差过电势对固相扩散系数的敏感度降低[4-6]。在电池老化实验中,常把动态激励电流设置在SOC约为40%处,此时,电池的dU/dQ取得最小值,正负电极都处于平台区。在平台区设置激励,可解耦Li+固相扩散过程的影响。

由于SOC 对过电势起着决定性的作用,把激励放置在特殊的SOC 下,可以削弱副反应对实验的影响。

阻抗谱检测ISC 是将镍钴锰(NCM)和石墨为电极的电池在50%SOC 下,通过电化学阻抗谱(EIS)进行评估。石墨负极和NCM 正极的EIS 大致验证了从数值模拟中获得的预测结果。当ISC 存在时,属于低频域的阻抗相位显著下降;以约1 Hz 中频阻抗表示的电荷转移电阻受到影响,影响方式与数值模拟的预测相符[7-9];高频阻抗保持相对稳定。EIS实验和构建模型的曲线表明,ISC 在低频范围内会导致过渡点向左移动,阻抗曲线有顺时针旋转的趋势[10]。

阻抗谱检测ISC 故障是以特定频率即低频区域下的阻抗曲线旋转为特征,普通电流激励的电压响应也有相应的数值规律。由于SOC 整体没有明显的电压升降规律,多数激励实验将注意力放在特定的SOC 值上,如0、40%和100%等。

1.2 实验设置

根据行业标准,允许归类为软短路的最大泄漏电流为C/3.7,表明典型商用电池的短路电阻为3～20 Ω[5]。实验采用额定容量为2.55 Ah 的18650 型锂离子电池(广东产),S/N 224359 充放电机(美国产),短路电池为并联33 Ω 电阻的电池。在25 ℃的SHP 恒温箱(北京产)中进行实验。

首先,对电池进行10 次2.5～4.2 V 完整的1C充放电,以激发活性,增强SEI 膜的稳定性,避免SEI 膜对实验的影响。在激励电流发出前后设置30 s 的空置时间,消除电池极化效应对实验产生的影响。使用小电流信号作为激励信号,可避免SOC 的升降对正常电池和模拟短路电池的对比产生影响。实验采用的充放电设备具有千分之一秒的采样频率,可捕捉激励的瞬时电压响应。

1.3 阶跃激励预实验测试

取1 只正常电池进行10 次1C充放电测试,完成测试后,对正常电池和模拟短路电池在恒流充放电期间施加小电流激励,激励波形选用阶跃信号。在电池充电期间,每充10%SOC,就静置一段时间并施加小电流充当阶跃信号。恒流测试的充电电流为1.25 A,激励电流为0.10 A,控制在充电电流的1/10 以内,激励时间设置为3 s。小电流会给电池带来一定的压升响应,见图1。

图1 阶跃信号刺激下各SOC 处的压升响应比较Fig.1 Comparison of voltage rise response at each state of charge(SOC)stimulated by step signal

从图1 可知,二者的差异并不明显。经过多次实验并尝试通过增大电流来加强差异,但效果仍不明显。由此可判断,阶跃信号不适合作为诊断内短路的激励信号。

2 结果与讨论

2.1 方波激励下的压升变化

方波信号是一种常见的非正弦曲线信号,选用0.2 A 的方波信号重复上述实验,结果表明,正常电池和模拟短路电池的电压响应升降并不固定。ISC 会产生漏电流,在电池充放电全周期,模拟短路电池的压升响应应低于正常电池,但实际情况并非如此。由于电池内部的副反应,在多处SOC 下出现了模拟短路电池的压升响应等于甚至大于正常电池的现象。在低SOC 下,漏电流的电荷量因占比提高加大了对电压响应的影响,方波激励下电池的充电曲线见图2。

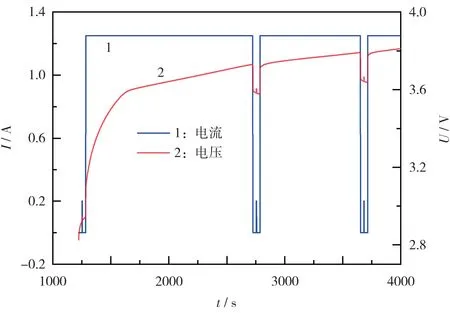
图2 低SOC 方波激励信号下的充电曲线Fig.2 Charging curves stimulated by square wave excitation signal under low SOC

从图2 可知,SOC 为0 处,施加小电流方波激励得到的正常电池的压升响应,大于模拟短路电池的压升响应。

取正常电池和模拟短路电池在SOC 为0 时的激励压升响应进行对比,4 次平行实验的结果见图3。

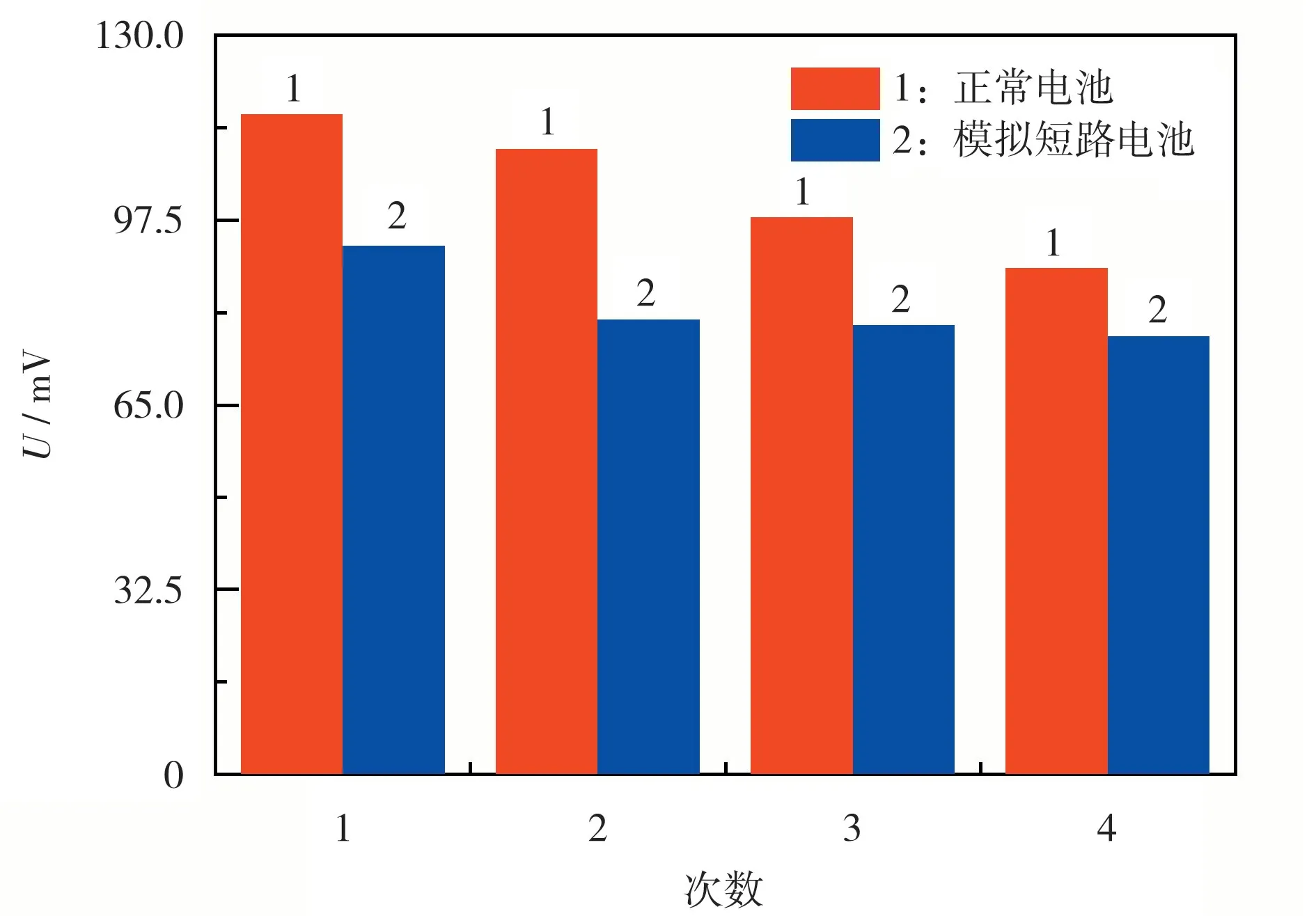
图3 方波激励下的SOC 为0 处的压升比较Fig.3 Comparison of voltage rise stimulated by square wave excitation with SOC of 0

从图3 可知,模拟短路电池的压升响应均小于正常电池,且方波信号比阶跃信号的差异敏感性高,更适合作为提取短路特征的激励信号。后续激励信号都选择方波信号,重点关注SOC 为0 处的激励响应。

为了避免实验的偶然性,在多组实验结束后,将33 Ω 的电阻换成66 Ω,电池短路程度明显变弱。实验数据显示,SOC 为0 时的压升规律依然保持。实验发现,不同老化程度的电池在同一SOC 下的压升响应不尽相同,同一老化程度下的电池在经历多次实验后,压升响应也略有区别。这表明,通过压升响应来检测电池内短路,需连续进行两次测试,并取两次测试结果进行比较,选取适当的阈值,当两次测试压升响应的差值超过阈值时,可判定为电池发生了内短路。

2.2 电压曲线分析

锂离子电池在恒流充放电的过程中时刻存在着极化效应。截取的方波激励信号在SOC 为0 前后电池的电压响应曲线如图4所示。

图4 正常电池与短路电池的电压响应曲线Fig.4 Voltage response curves between normal battery and short circuit battery

从图4 可知,当方波激励结束后,由于极化效应,电压还会上升一段时间。模拟短路电池的电压会比正常电池上升得更慢,电压曲线偏转较为平缓。出现这种漏电流偏移现象的原因是,模拟短路电池在运行过程中一直存在漏电流,漏电流产生的压降抵消了一部分极化效应的影响。实验之所以要在小电流激励下降之后再进行观察,是因为小电流持续通过的时间非常短,对电池本身的SOC 影响可忽略不计,电压升降的范围较小,放大了漏电流的作用。

2.3 参数阈值设置

锂离子电池的充放电过程就是Li+在电池正负极之间嵌脱的过程。这一过程并非瞬间完成,电池的状态在正常情况下并不会发生突变。为进一步量化短路程度与激励响应的关系,取激励后静置30 s 的压升(Up)与激励2 s 的压升(Ug)的比值,作为参数Yt[见式(1)],来反映短路程度的大小。

取1 只实验电池进行3 次不同短路程度的检测实验,并在实验后增加1 只实验电池,同时对两只电池进行30 次充放电,结果列于表1、表2。

表1 不同短路程度3 次实验Yt 值Table 1 Yt values of three experiments for different short circuit degree

表2 不同老化程度下两只电池的Yt、Up 值Table 2 Yt and Up values of two batteries under different aging level

从表1、表2 可知,激励后静置30 s 的压升(Up)与激励2 s 的压升(Ug),均与激励电流的大小有关;30 s 的静置时间基本能消除2 s 的0.2 A 激励电流带来的极化效应,使电压相对稳定;之所以将电流大小定为0.2 A、时间定为2 s,是为了尽可能减小对SOC 的影响,提高检测的有效性和准确性。Yt是静置压升与激励压升的比值,没有实际物理意义,但能在一定程度上反映漏电流对极化效应的影响;采用比值而非直接用静置压升来反应极化,优势在于可以放大漏电流的作用,使短路电池与正常电池的数据差异更明显。

Yt和Up是电池在极化效应下的压升参数,受短路程度和老化程度的共同影响,无法解耦,但对比表1、表2 可知,Yt受短路程度的影响较大,Up受老化程度的影响较大。根据这一特性,在检测时,可将Up的检测顺序排在Yt之前,当Up变化较小且Yt小于阈值时,即可判定电池发生了短路。短路阈值需要根据安全需求来设置,如实验设定阈值为Yt=2,在激励检测中,可检测120 Ω 以内的短路。

在实际应用中,电池通常不会放电至SOC 为0。为了寻找合适的诊断放电SOC 区间,放电过程中在SOC 为28%、19%、7%、2%和0 处设置激励点。低SOC 放电方波激励的电压电流曲线见图5。

正常电池与并联了113 Ω 电阻的模拟内短路电池的放电过程Yt值见图6。

图6 低SOC 正常电池与模拟短路电池各激励点的Yt 值Fig.6 Yt values on excitation points for low SOC between normal battery and simulated short circuit battery

从图6 可知,SOC 降低至2%后,短路电池的Yt显著小于正常电池。因此,在实际应用中,可在电池使用至低电量(SOC 为5%～1%)后施加激励,取得Yt值与阈值比较,以判断是否存在内短路。

2.4 电池组的激励检测

为研究该方法在电池组中的适用性,对若干电池进行容量测试,挑选8 只容量一致性较好的电池串联成组,在SOC分别为28%、19%、7%、2%处设置放电激励点,进行放电激励测试。

随机挑选电池组内1 只电池(实验选取6 号电池),并联98 Ω 电阻,模拟内短路,再次进行放电激励测试,收集各参数。由于电池组是串联的且一致性较好,在电池组的检测中,可通过比较各自Up和Yt两个参数的差异,无需仿照新电池流程设置阈值。将电池组放电至SOC 为2%,Yt、Up值如图7所示。

图7 SOC 为2%时电池组中各电池的Up、Yt 值对比Fig.7 Comparison of Up and Yt values of each battery in battery pack when SOC is 2%

从图7 可知,模拟短路的6 号电池,Up值最高,同时Yt值最低,说明可以将特征值Up与Yt联合起来,作为判断的标准。

3 结论

本文作者针对18650 型锂离子电池进行内短路模拟实验,提出单体短路电池在常见电流激励信号下与正常单体电池的响应差异特征,在此基础上形成内短路检测方法,最后,将该方法推广至电池组内短路的检测,给出电池组内短路检测的判断依据。

实验结果表明,当SOC 接近0 时,短路电池的压升响应低于正常电池,电压曲线也出现了比正常电池更平缓的偏移现象。这一规律在SOC 越低时越明显。利用参数设置Yt阈值可检测120 Ω 以内的短路。该方具有一定的商业用途,如在充放电机设备上内嵌一个小电流发射装置,接入数据采集系统,在充电时记录压升和Yt值,即可通过判断Yt与阈值的相对关系,判断电池组是否存在内短路。

进一步的研究,可关注于将电池短路程度量化反射在压升响应及Yt、Up参数的量化。